Поделиться
ПРОЕКТ,ЛИТВИНЕНКО АЛЕКСАНДРА,7 Б.docx
Министерство образования Республики Казахстан
Управление образования Павлодарской области
Региональный научно-практический центр «Ертіс дарыны»
 |
Литвиненко Александра, Мельникова София
(Фамилия, имя)
7 «Б» СЫНЫБЫ
(класс)
Тема:
Симметрия в алгебре.
Секция: математика, информатика
Ғылыми жетекшісі: Титченко Анжелика Петровна
математика мұғалімі
Павлодар
2019-2020 оқу жылы
Оглавление
Введение…………………………………………………………………..
Глава 1. Симметрия в алгебре.
1.1 Симметрия в линейной алгебре. Симметрия матриц.
1.2 Линейная алгебра
1.2 Основные конструкции. Матрицы и определители.
1.3 Векторы.
1.4 Применение.
Глава 2. Симметрия в теории множеств.
2.1Симметричное отношение.
2.2 Множество
2.3 Примеры.
Глава 3. Симметрия в теории вероятности.
3.1 Возникновение теории вероятностей
3.2 Подинтервалы и непрерывное равномерное распределение.
3.3 Принцип симметрии и случайные процессы.
3.3 Применение.
АННОТАЦИЯ
В современных условиях одной из основных задач школы является интеллектуальное развитие учащихся, формирование исследовательских умений, создание условий для реализации потенциальных возможностей ребенка в процессе обучения. В этом плане актуальной и интересной является исследовательская работа учениц 7 «Б» класса Литвиненко Александры и Мельниковой Софии «Симметрия в алгебре». Данная тема посвящена изучению и доказательству теоремы для общего метода решения систем высших степеней и поэтому имеет важное значение для воспитания абстрактного мышления ученика, то есть для формирования определенных способов умственных действий – формирование умений самостоятельно приобретать знания, развитие интеллектуальных, учебно-исследовательских умений и навыков.
Данная исследовательская работа имеет большую практическую значимость. В отличие от метода исключения, доказанный метод приводит не к повышению, а к понижению степени уравнений, что позволяет их решать более рациональным способом.
Метод, о котором идет речь, основан на использовании теории так называемых симметрических многочленов. Теория позволяет решать не только многие системы алгебраических уравнений, но и различные другие алгебраические задачи (решение иррациональных уравнений, доказательство тождеств и неравенств, разложение на множители и т. д.). Ряд задач этих типов разобран в тексте проекта, а в и конце каждого раздела предложены задачи для самостоятельного решения. Среди этих задач есть и весьма трудные; некоторые из них предлагались на математических олимпиадах. С помощью теории симметрических многочленов решение этих задач заметно упрощается и, что самое главное, проводится стандартным приемом.
Исследовательская работа структурно выстроена правильно, логична, четко сформулированы цель и задачи, присутствуют моменты исследования научного характера и заключение по работе. Ученица исследовала материал, выходящий за рамки школьной программы, сопровождается самостоятельно найденными выкладками иллюстративного характера. Содержание отвечает выбранной теме, которая раскрыта достаточно, учитывая возраст авторов работы.
Рассматривается понятие симметрии в математике, при этом использует не только материал учебного пособия, но и дополнительный материал, предназначенный для углубленного изучения.
Исследовательская работа четко структурирована, грамотно изложена, прослеживается логическая связь между частями работы, отличается завершённостью. Автором использованы общенаучные термины.
В работе ученица проявила исследовательские качества, установила и доказала новый метод, показала самостоятельность в изучении большого объема специализированной источников информации, компьютерную грамотность в оформлении и создании презентации к защите.
Работа заслуживает высокой оценки.
Введение
Одним из самых сложных разделов школьной алгебры является решение систем уравнений высших степеней.
Для квадратного уравнения с одним неизвестным выводится формула нахождения корней ,указывающая стандартный путь решения.
Для систем уравнений первой степени тоже есть стандартные приемы решения (исключение неизвестных, уравнивание коэффициентов и т. д.). Однако для систем уравнений высших степеней дело обстоит сложнее.
Наиболее общим способом решения таких систем является метод исключения неизвестных. Мы поясним его на примере следующей системы уравнений:
x + y=4,
2x2 + y2 = 19.
Решим первое уравнение относительно неизвестного y. Мы находим y =4 x. Подставив полученное для y выражение во второе уравнение, получаем новое уравнение, содержащее только одно неизвестное x.
После очевидных упрощений приходим к уравнению решая которое, находим два корня.
Каждому из этих корней соответствует определенное значение y .
Проверка показывает, что оба найденных решения удовлетворяют заданной системе уравнений.
Метод исключения неизвестных является весьма общим. Теоретически из любой системы двух алгебраических уравнений с двумя неизвестными можно, исключая одно неизвестное, получить уравнение относительно второго неизвестного. Однако не всегда процесс исключения является столь простым, как в разобранном выше примере.
Наибольшим же неудобством метода исключения является то, что он часто приводит к уравнению очень высокой степени. Доказано, что если одно уравнение системы (содержащей два неизвестных) имеет степень n, а второе — степень m, то после исключения, как правило, получается уравнение степени m*n.
Из первого уравнения находим: x2 =5 y2, и потому x2 =(5 y2)3 =125 75y2 +15y4 y6.
Точно так же из второго уравнения получаем: x3 =9 y3, и потому x6 =81 18y3 + y6.
Приравнивая найденные значения для x6, получаем уравнение, со-держащее только одно неизвестное y: 2y6 15y4 18y3 +75y2 44=0.
Однако это уравнение имеет ш е с т у ю степень (2 3=6 — в полном соответствии с упомянутой теоремой ), а формулы для решения уравнений шестой степени у школьника нет! Таким образом, метод исключения завел нас в тупик.
Из-за этих недостатков метод исключения (при решении систем уравнений высших степеней) используют довольно редко. Обычно стараются решить систему с помощью какого-нибудь искусственного приема. Но общих правил отыскания таких приемов нет. Каждая система решается своим методом, и опыт, полученный при решении одной системы, мало помогает при решении другой. В результате мы получаем набор головоломок и отдельных кустарных методов их решения.
Цель проекта — найти и доказать довольно общий метод решения систем уравнений высших степеней.
Он оказался не столь универсален, как метод исключения, так как может быть применен не ко всякой системе.
Гипотеза- метод применим к большинству систем, изучаемых в школьном курсе алгебры.
Актуальность-в отличие от метода исключения, найденный и доказанный нами метод приводит не к повышению, а к понижению степени уравнений, что позволяет их решать более рациональным способом.
Метод, о котором идет речь, основан на использовании теории так называемых симметрических многочленов.
Теория очень проста и что она позволяет
решать не только многие системы алгебраических уравнений, но и различные другие
алгебраические задачи (решение иррациональных уравнений, доказательство
тождеств и неравенств, разложение на множители и т. д.). Ряд задач этих типов
будет разобран в тексте нашего проекта, а в и конце каждого раздела мы
предлагаем задачи для самостоятельного решения. Среди этих задач есть и весьма
трудные; некоторые из них предлагались на математических олимпиадах. С помощью
теории симметрических многочленов решение этих задач заметно упрощается и, что
самое главное, проводится стандартным приемом.
Рассмотрим примеры симметрических многочленов.
Среди наиболее трудных задач на решение систем уравнений высших степеней мы находим следующие:
Все эти системы имеют одно общее свойство — левые части уравнений являются многочленами, в которые x и y входят одинаковым образом. Именно для таких систем уравнений и применимы излагаемые нами методы решения.
Многочлены, в которые x и y
входят одинаковым образом, называют симметрическими. Точнее говоря:
многочлен от x и y называют
симметрическим, если он не изменяется при замене x на y, а
y на x.
Многочлен x2y + xy2 — симметрический.
Приведем важнейшие примеры симметрических многочленов. Как известно из арифметики, сумма двух чисел не меняется при перестановке слагаемых, т. е.
x + y = y + x для любых чисел x и y.
Это равенство показывает, что многочлен x + y является симметрическим.
Точно так же из закона коммутативности (Коммутативность -
свойство математической операции, наличие которого обеспечивает независимость результата выполнения
данной операции от порядка следования
элементов (аргументов операции) для всех элементов множества
на котором данная операция определена. Можно говорить о коммутативности
некоторой бинарной
операции (например композиции -
"умножения"):
a∗b=b∗a,∀a,b∈Qa∗b=b∗a,∀a,b∈Q, где QQ - множество, на котором определена
операция ∗) умножения xy
= yx следует, что произведение xy является симметрическим
многочленом. Симметрические многочлены x + y и xy являются
самыми простыми. Их называют элементарными симметрическими многочленами от
x и y. Для них используем специальные обозначения: s1
= x + y, s2 = xy.
Кроме s1 и s2, нам часто будут встречаться так называемые степенные суммы, т. е. многочлены x2 + y2, x3 + y3, . . ., xn + yn, . . .
Принято обозначать многочлен xn + yn через sn. Таким образом,
s1 = x + y,
s2 = x2 + y2,
s3 = x3 + y3,
s4 = x4 + y4,
. . . . . . .
Рассмотрим простой прием, позволяющий получать симметрические многочлены. Возьмем любой (вообще говоря, не симмерический) многочлен от s1 и s2 и подставим в него вместо s1 и s2 их выражения через x и y. Ясно, что при этом мы получим симметрический многочлен от x и y (ведь ни s1 = x + y, ни s2 = xy не меняются при перестановке местами x и y, а потому не меняется и весь получившийся многочлен, выражающийся через x + y и xy). Например, из многочлена s13 s1s2 получаем симметрический многочлен (x + y)3 (x + y)xy = x3 +2x2y +2xy2 + y3.
Итак,
если взять любой многочлен от s1
и s2 и подставить в него вместо s1
s2 их выражения s1 = x + y, s2 = xy, то получится симметрический многочлен от x и y.
Возникает вопрос, является ли этот прием построения симметрических многочленов общим, т. е. можно ли с его помощью получить любой симметрический многочлен?
Рассмотрение примеров делает это предположение вероятным. Например, степенные суммы s1, s2, s3, s4 без труда выражаются через s1 и s2:
s1 = x + y = s1;
s2 = x2 + y2 =(x + y)2 2xy = s12 2s2;
s3 = x3 + y3 =(x + y)(x2 xy + y2)=(x + y)((x + y)2 3xy)= s1(s12 3s2);
s4 = x4 + y4 =(x2 + y2)2 2x2y2 =(s12 2s2)2 2s22.
В качестве следующего примера возьмем симметрический многочлен x3y + xy3. Мы имеем: x3y + xy3 = xy(x2 + y2)= s2(s12 2s2).
Разбор дальнейших примеров дает тот же результат:
какой бы симметрический многочлен мы ни взяли, после более или менее сложных
выкладок его удается выразить через элементарные симметрические многочлены s1
и s2. Таким образом, примеры приводят нас к предположению о
справедливости следующей теоремы о симметрических многочленах от двух переменных
:
Те о р е м а. Любой симметрический многочлен от x и y можно представить в виде многочлена от s1 = x + y и s2 = xy.[1, 47]
Разумеется, даже миллион разобранных примеров не может заменить доказательства всегда остается опасность, что найдется миллион первый симметрический многочлен, не выражающийся через s1 и s2.
Переходим к доказательству
сформулированной теоремы. Мы проведем его в два приема.
Выражение степенных сумм через σ1 и σ2. Сначала мы докажем теорему не для любых симметрических многочленов, а лишь для степенных сумм. Иными словами, мы установим, что каждую степенную сумму sn = xn + yn можно представить в виде многочлена от s1 и s2.
С
этой целью мы умножим обе части равенства sk 1 = xk
1 + yk 1 на s1 = x
+ y. Получим:
s1sk 1 =(x + y)(xk 1 + yk 1)= xk + xyk 1 + xk 1y + yk =
= xk + yk + xy(xk 2 + yk 2)= sk + s2sk 2.
Из этой формулы и вытекает справедливость нашего утверждения.
В самом деле, раньше мы уже проверили , что степенные суммы s1 и s2 представляются в виде многочленов от s1 и s2. Но если нам уже известно, что степенные суммы s1, s2, . . ., sk 2, sk 1 выражаются в виде многочленов от s2 и s2, то, подставляя эти выражения формулу (1), мы получим выражение степенной суммы sk через s1 и s2. Иными словами, мы можем последовательно находить выражения степенных сумм через s1 и s2: зная s1 и s2, находим по формуле (1) s3, затем s4, s5 и т. д. Ясно, что рано или поздно мы получим выражение любой степенной суммы sn через s1 и s2. Таким образом, наше утверждение доказано.
Формула (1), составляющая основу изложенного доказательства, позволяет не только утверждать, что sn как-то выражается через s1 и s2, но также позволяет последовательно вычислять выражения степенных сумм sn через s1 и s2. Так, с помощью формулы (1) мы последовательно находим:
s3 = s1s2 s2s1 = s1(s12 2s2) s2s1 = s13 3s1s2;
s4 = s1s3 s2s2 = s1(s13 3s1s2) s2(s12 2s2)= s14 4s12s2 +2s22;
s5 = s1s4 s2s3 = s1(s14 4s12s2 +2s22) s2(s13 3s1s2)= s15 5s13s2 +5s1s22
Примененный метод доказательства носит
название метода математической индукции. Сравним полученные
значения степенных сумм s3 и s4 с
формулами, которые были получены.
В табл. 1 сведены выражения степенных сумм s1, s2, . . . , s10 через s1 и s2; эти выражения будут нам полезны при решении за-дач.
Теперь нетрудно завершить доказательство теоремы.
Любой симметрический многочлен от x и y содержит (после приведения подобных членов) слагаемые двух видов.
Во-первых, могут встретиться одночлены, в которые x и y входят
одинаковых степенях, т. е. одночлены вида axkyk. Ясно, чтоaxkyk = a(xy)k = as2k,
то есть одночлены этого вида непосредственно выражаются через s2.
Во-вторых, могут встретиться одночлены, имеющие разные степени относительно x и y, т. е. одночлены вида bxkyl, где k 6=l. Ясно, что вместе с одночленом bxkyl симметрический многочлен содержит также и одночлен bxlyk, получаемый из bxkyl перестановкой букв x и y. Иными словами, в симметрический многочлен входит двучлен вида b(xkyl + xlyk). Предполагая для определенности k < l, мы сможем переписать этот двучлен следующим образом:b(xkyl + xlyk)= bxkyk(yl k + xl k)= bsks .2 l k
так как по доказанному степенная сумма sl k представляется в виде многочлена от s1 и s2, то и рассматриваемый двучлен выражаетсячерез s1 и s2.
Итак, каждый симметрический многочлен представляется в виде суммы одночленов вида axkyk и двучленов вида b(xkyl + xlyk), каждый из которых выражается через s1 и s2. Следовательно, любой симметрический многочлен, представляется в виде многочлена от s1 и s2. Теорема полностью доказана.
Рассмотрим пример. Пусть дан симметрический многочлен
f(x, y)= x5 +3x3y2 x3y3 +2xy4 7x2y2 + y5 +3x2y3 5xy3 5x3y +2x4y.
Разбивая его на одночлены и двучлены, как указано в доказательстве, получаем:
f(x, y)= x3y3 7x2y2 +(x5 + y5)+3(x3y2 + x2y3)+2(xy4 + x4y) 5(xy3 + x3y),
или, иначе, f(x, y)= x3y3 7x2y2 +(x5 + y5)+3x2y2(x + y)+ +2xy(x3 + y3) 5xy(x2 + y2)=
s23 7s22 + s5 +3s22s1 +2s2s3 5s2s2.
Подставляя, наконец, выражения степенных сумм через s1 и s2 (см.табл. 1), получаем окончательно:f(x, y)= s23 7s22 +(s15 5s13s2 +5s1s22)+3s1s22 +2s2(s13 3s1s2) 5s2(s12 2s2)=s15 3s13s2 5s12s2 +2s1s22 s23 +3s22. .[1, 89]
Мы видим, что если дан симметрический многочлен от x, y (не слишком высокой степени), то выразить его через s1 и s2 несложно. Изложенное выше доказательство основной теоремы как раз и содержит прием, позволяющий выразить любой симметрический многочлен f(x, y) через элементарные симметрические многочлена s1 и s2. Естественно возникает вопрос: не может ли найтись какой-либо другой прием, который приведет к иному выражению многочлена f(x, y) через s1 и s2?
Оказывается, что это невозможно: каким бы путем мы ни воспользовались для выражения симметрического многочлена f(x, y) через s1 и s2, мы всегда получим один и тот же результат. Иными словами, справедлива следующая теорема
Т е о р е м а е д и н с т в е н н о с т
и. Если многочлены f(s , s ) и y(s , s
)
1 2 1 2
при подстановке s1 = x + y, s2 = xy превращаются в один и тот же симметрический многочлен f(x, y), то они совпадают**): f(s1, s2)= y(s1, s2).
Линейная алгебра — это раздел математики, изучающий векторы, векторные пространства, линейные преобразования и системы линейных уравнений. Линейная алгебра первоначально и возникла как наука о решении систем линейных алгебраических уравнений. Впоследствии её предмет расширился, и сейчас она представляет собой теорию линейных преобразований (операторов) в конечномерных векторных пространствах (точный смысл сказанного станет ясен в дальнейшем). .[2, 38]
Транспонированная
матрица — матрица , полученная из
исходной матрицы 
заменой строк на столбцы.
Формально, транспонированная матрица для матрицы размеров — матрица размеров , определённая как .
То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.
Свойства транспонированных матриц:
· Дважды транспонированная матрица А равна исходной матрице А.
· Транспонированная сумма матриц равна сумме транспонированных матриц.
· Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
· При транспонировании можно выносить скаляр.
Определитель транспонированной матрицы равен определителю исходной матрицы.
Определитель матрицы или детерминант матрицы - это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.
Определителем матрицы n×n будет число:
|
det(A) = |
Σ |
(-1)N(α1,α2,...,αn)·aα11·aα22·...·aαnn |
|
(α1,α2,...,αn) |
где (α1,α2,...,αn) - перестановка чисел от 1 до n, N(α1,α2,...,αn) - число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.
Обозначение
Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).
Свойства определителя матрицы
· Определитель единичной матрицы равен единице:det(E) = 1
· Определитель матрицы с двумя равными строками (столбцами) равен нулю.
· Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
· Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
· Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
· При транспонировании значение определителя матрицы не меняется:det(A) = det(AT)
· Определитель обратной матрицы:det(A-1) = det(A)-1
· Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
· Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
· Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
· Общий множитель в строке (столбце) можно выносить за знак определителя:
a11a12...a1na21a22...a2n....k·ai1k·ai2...k·ain....an1an2...ann = k·a11a12...a1na21a22...a2n....ai1ai2...ain....an1an2...ann
· Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kn·det(A), где A матрица n×n, k - число.
·
Если
каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то
исходный определитель равен сумме двух определителей, в которых вместо этой
строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают
с исходным определителем:
a11a12...a1na21a22...a2n....bi1 + ci1bi2 + ci2...bin + cin....an1an2...ann = a11a12...a1na21a22...a2n....bi1bi2...bin....an1an2...ann + a11a12...a1na21a22...a2n....ci1ci2...cin....an1an2...ann
· Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
· Определитель произведения матриц равен произведению определителей этих матриц:det(A·B) = det(A)·det(B) .[3, 112]
Методы вычисления определителя матрицы
Вычисление определителя матрицы 1×1
Правило:
Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:∆ = |a11| = a11
Вычисление определителя матрицы 2×2
Правило:
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:
|
∆ = |
|
= a11·a22 - a12·a21 |
Пример 1.Найти определитель матрицы A
|
A = |
|
Решение:
|
det(A) = |
|
= 5·1 - 7·(-4) = 5 + 28 = 33 |
Вычисление определителя матрицы 3×3
Правило треугольника для вычисления определителя матрицы 3-тего порядка
Правило:
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
|
|
|
|
|
+ |
– |
|
∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
Правило Саррюса для вычисления определителя матрицы 3-тего порядка
Правило:
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":
|
∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
Пример 2.
Найти определитель матрицы A = 571-410203
Решение: det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 - 1·1·2 - 5·0·0 - 7·(-4)·3 = 15 + 0 + 0 - 2 - 0 + 84 = 97
В линейной алгебре симметричная матрица — это квадратная матрица, которая не меняется при транспонировании. Формально матрица A симметрична, если
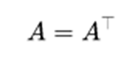
и, по определению равенства матриц, размеры матриц должны совпадать, так что только квадратная матрица может быть симметричной. Элементы симметричной матрицы симметричны относительно главной диагонали. Таким образом, если элементы матрицы равны A = (aij), то aij = aji для всех индексов i и j.
Примеры симметричных матриц.[4, 93]
В теории матриц часто встречается понятие «равенство матриц». Что подразумевается под этим понятием?
Определение 1
Матрица A=(aij)m×nA=(aij)m×n равна матрице B=(bij)k×lB=(bij)k×l при условии, если у них одинаковые размерности и соответствующие элементы равны между собой.
Пример 1
Для матриц 2-го порядка можно записать равенство в таком виде:
A=(a11a12a21a22), B=(b11b12b21b22)A=B⇒a11=b11, a12=b12, a21=b21, a22=b22A=a11a12a21a22, B=b11b12b21b22A=B⇒a11=b11, a12=b12, a21=b21, a22=b22
Пример 2
Определить, равны ли матрицы:
1. A=(20−13), B=(20−13)2. A=(20−13), B=(−32)3. A=(20−13), B=(2413)1. A=20-13, B=20-132. A=20-13, B=-323. A=20-13, B=2413
Решение:
1. A=(20−13), B=(20−13)1. A=20-13, B=20-13
У матриц А и В одинаковая размерность (одинаковый порядок), равный 2×2. Соответствующие элементы равны, следовательно равны и матрицы.
2. A=(20−13), B=(−32)2. A=20-13, B=-32
Матрицы А и В имеют разный порядок, равный 2×2 и 2×1.
3. A=(20−13), B=(2413)3. A=20-13, B=2413
У матриц А и В одинаковый порядок, который равен 2×2. Однако не все соответствующие элементы равны между собой, поэтому матрицы не равны.
Симметричная матрица – это матрица, элементы которой симметричны относительно главной диагонали.
Пример симметричной матрицы
ПРИМЕР 1
|
Задание |
Известно,
что матрица |
|
|
|
Следующая матрица 3×3 симметрична:
Любая квадратная диагональная матрица симметрична, поскольку все её недиагональные элементы равны нулю.
Соответствующий объект для комплексного унитарного пространства — Эрмитова матрица с комплексными элементами, которая равна своей Эрмитово-сопряжённой матрице. Таким образом, в линейной алгебре над комплексными числами часто под симметричной матрицей подразумевается матрица с вещественными элементами. Симметричные матрицы появляются естественным образом в различных приложениях и, как правило, пакеты линейной алгебры для них имеют выделенные процедуры.
Эрмитово-сопряжённая матрица или сопряжённо-транспонированная матрица — это матрица A* с комплексными элементами, полученная из исходной матрицы A транспонированием и заменой каждого элемента комплексно-сопряжённым ему.
Линейная алгебра обобщена средствами общей алгебры, в частности, современное определение линейного (векторного) пространства опирается исключительно на абстрактные структуры, а многие результаты линейной алгебры обобщены на произвольные модули над кольцом. Более того, методы линейной алгебры широко используются и в других разделах общей алгебры, в частности, нередко применяется такой приём, как сведение абстрактных структур к линейным и изучение их относительно простыми и хорошо проработанными средствами линейной алгебры, так, например, реализуется в теории представлений групп. Функциональный анализ возник как применение методов математического анализа и линейной алгебры к бесконечномерным линейным пространствам, и во многом базируется на методах линейной алгебры и в дальнейших своих обобщениях. Также линейная алгебра нашла широкое применение в многочисленных приложениях (в том числе, в линейном программировании, в эконометрике и естественных науках.
Матрица — математический
объект, записываемый в прямоугольной таблице размером 
, в ячейках
которой расположены элементы произвольного заранее выбранного (основного) поля
(в наиболее общем случае — ассоциативного кольца) — это могут быть целые,
вещественные или комплексные числа, векторы, рациональные функции — в
зависимости от приложений и задач:
Для матриц используется также
сокращённая запись 
, но обычно
с матрицами оперируют как с едиными объектами: над матрицами определены
сложение и умножение, также матрицу можно умножить на скаляр — элемент
основного поля, относительно этих операций образуют векторное пространство над
основным полем (или, в наиболее общем случае — модуль над кольцом). Другие
операции над матрицами — транспонирование (замена строк на столбцы) и
псевдообращение (обобщение обращения квадратных матриц). Матрицы размера 
называются вектор-строка и вектор-столбец
соответственно.
Понятие вектора изначально возникло как геометрическая абстракция для объектов, характеризующихся одновременно величиной и направлением, таких как скорость, момент силы, напряжённость электрического поля, намагниченность. В начале XX века изначальная интерпретация векторов (до сих пор используемая в элементарной математике) как «направленных отрезков» сменилось на аксиоматику векторного пространства с двумя операциямиː сложением векторов и умножение вектора на числа (более общо, на элементы поля). Кроме того, часто вводятся различные виды произведения векторов: скалярное, векторное, смешанное, псевдоскалярное, двойное векторное.
Ключевую роль в линейной
алгебре играет понятие линейной независимости векторов, которое лежит в основе
определений базиса и размерности векторного пространстваː число n
называется размерностью векторного пространства, если оно содержит n линейно
независимых векторов и любые k>n векторов этого пространства являются
линейно зависимыми. Такое векторное пространство называется n-мерным, и любой
его вектор представляется упорядоченной последовательностью n чисел (однозначно
определяемых при выборе какого-либо базиса). Таким образом, векторы могут быть
записаны в виде матриц размера 
— векторов-столбцов и векторов-строк соответственно, а все операции
векторной алгебры могут быть сведены к алгебре матрицː например, сложение
векторов совпадает со сложением матриц, а векторное умножение векторов может
быть выражено как произведение кососимметрической матрицы, построенной из
первого сомножителя и вектора-стоблца, представляющего второй сомножитель.
Система m линейных алгебраических уравнений с n неизвестными — это система уравнений вида
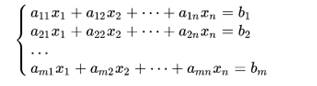
Она может быть представлена в матричной форме как:
Или: 
Мы называем отношение симметричным, если каждый раз, когда выполняется от A к B, то выполняется и от B к A. Заметим, что симметрия не является противоположностью антисимметрии.
Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.
Существуют два основных способа задания множеств: перечисление и описание.
Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество.
Например, множество Y неотрицательных чётных чисел, меньших 10 можно задать в виде списка: Данный способ удобно применять лишь к ограниченному числу конечных множеств.
Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка. В таком случае множества определяются свойствами их элементов. Множество Y задано, если указано условие, которому удовлетворяют все элементы, принадлежащие множеству Y и которому не удовлетворяют элементы, не принадлежащие множеству Y.
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины, также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
В случае конечного числа возможных событий симметрия, учитывающая перестановки (перенумерации), даёт дискретное равномерное распределение. В случае, когда события представляют собой интервал вещественных чисел, симметрия, учитывающая перестановки подинтервалов равной длины, соответствует непрерывному равномерному распределению.
Непрерывное равномерное распределение — в теории вероятностей — распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна.
Вероятность — степень возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным.
Предположим, что несколько точек брошены случайным образом на отрезок [0; 1]. Например, пусть это точки w, x и y, как показано на рисунке
Эти три точки делят наш отрезок на четыре части с длинами х,у – х,w – y,1 – w.
Если процедура бросания повторяется, то по-прежнему мы получаем четыре отрезка (левый, второй, третий и правый), и можно поставить вопрос о распределении длины, скажем, левого промежутка.
Фиксируем некоторое число t. Какова вероятность того, что все три точки упадут справа от t? Так как бросания независимы, и вероятность того, что каждая точка упадет справа от t, равна 1 – t, то ответом на поставленный вопрос является (1 – t)3.
Итак, P (левая точка лежит справа от t) = (1 – t)3.
В то время как распределение длины левого промежутка находится просто, а распределение длины правого из соображений симметрии совпадает с распределением левого, задача нахождения распределения длин второго и третьего промежутков может представить известные трудности. Может быть, читатель уже догадался, что эти распределения равны распределению длины левого промежутка, но так, впрочем, думают совсем немногие. Целью следующих замечаний и является разъяснение этого факта.
Вместо того, чтобы бросать точки на единичный отрезок, будем бросать их на окружность единичной длины. При этом вместо трех точек используем четыре, причем четвертую точку обозначим через z.
Таким образом, точки x, y и w, как и раньше, размещены на единичном интервале, у которого, однако, случайные концы. В силу равноправности всех четырех точек длины дуг (z; x), (x; y), (y; w) и (w; z) имеют одно и то же распределение. Если процесс бросания производится несколько раз, и при каждом бросании вычисляется длина дуги от точки z до следующей против часовой стрелки, от этой – так же до следующей и т.д., то имеет смысл говорить о распределении длин этих дуг, причем для всех дуг это распределение одинаково.
Разрывая окружность в точке z и разворачивая ее в отрезок, видим, что бросание четырех точек на окружность, одна из которых используется как начало отсчета, эквивалентна бросанию трех точек на единичный интервал. Мы не дадим здесь строгого доказательства, хотя читатель, быть может, и не вполне убежден предыдущими рассуждениями. Верен общийпринцип симметрии: При бросании n точек наудачу на отрезок, распределение длин n + 1 получающихся при этом отрезков одинаково.
Рассмотрим теперь несколько задач, где можно использовать этот принцип.
1) Из хорошо перетасованной колоды в 52 карты, содержащей четыре туза, извлекаются сверху карты до появления первого туза. На каком месте в среднем появляется первый туз?
Решение: Естественно считать, что принцип симметрии сохраняется и для дискретных распределений. Четыре туза делят колоду на 5 частей, каждая из которых содержит от 0 до 48 карт. Если два туза лежат подряд, то будем говорить, что длина соответствующего куска колоды равна нулю. Аналогично нулевую длину имеют части колоды, которые находятся до первого туза, если он лежит сверху, и за четвертым тузом, если он является последней картой в колоде. Согласно принципу симметрии средняя длина каждой части равна 48/5 = 9,6. Последующей картой должен быть туз, который является, таким образом, в среднем 10,6 картой. .[8]
Решение систем уравнений
Пример 1. Решить систему уравнений
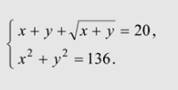
Если обозначить
, то из первого уравнения системы следует, что 
,
где 
. Так как положительный корень 
,
то
и имеет место система уравнений
Так как 
, то из второго уравнения системы следует
или 
. Корнями
квадратного уравнения являются 
и 
Решение простейшей задачи
Задача 1.
Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения – за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.
Решение:
Вспомним уравнение прямолинейного равномерного движения:
S – расстояние,
V – скорость,
T – время.
Переведем 2 часа 48 минут в часы, это составит
Пусть х км/ч- скорость лодки
в стоячей воде, у км/ч – скорость течения реки. Составим математическую модель.
Если лодка движется по течению, то она имеет скорость х+у км/ч и пройдет за время 
Если лодка движется против течения, она идет со
скоростью х-у км/ч и пройдет 14 км за время 
По течению 14
Против течения 14
Решим полученную систему.
Ответ: 6 км/ч; 1 км/ч.
Решение опорных задач
Перед тем как приступить к более сложным задачам, решим две опорные задачи на движение.
1. Первая опорная задача (сближение).
Из пунктов А и В одновременно выехали навстречу друг другу два поезда.
Дано:
AB=S
x, y – скорости поездов, км/ч.
Найти: Время t до их встречи, и расстояния пройденные до момента их встречи каждым из поездов.
Решение:
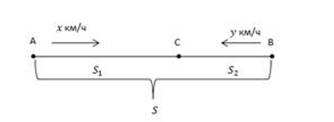
Найдем скорость сближения: х+у
Найдем время t = 
Найдем искомые расстояния: 
= 
Ответ: 
2. Вторая опорная задача.
Первый турист вышел из пункта А. Одновременно второй турист вышел из пункта В. Оба двигаются в направлении луча АВ. Первый догнал второго в пункте С.
Дано:
AB = S
x, y – скорости первого и второго туристов, км/ч.
Найти: Время t до встречи
туристов, расстояния 
пройденные первым и вторым туристами до встречи.
Решение:
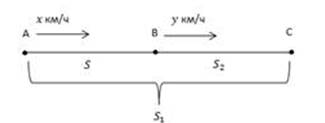
Найдем скорость сближения: х-у
Найдем время t до встречи: 
Найдем искомые расстояния: 
Ответ: 
Решение задач
Задача 1.
Из двух городов, расстояние между которыми 700 км, одновременно навстречу друг другу отправляются два поезда, и встречаются через 5 часов. Если второй поезд отправится на 7 часов раньше первого, то они встретятся через два часа после отправления первого поезда. Найти скорость каждого поезда.
Решение:
Пусть x км/ч, y км/ч – скорости первого и второго поездов.
S – расстояние между городами.
Рассмотрим вначале первый случай. Легко увидеть, что это задача на сближение, т.е. мы сможем пользоваться данными, полученными в первой опорной задаче.
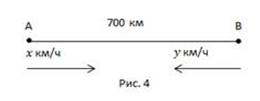
700 км оба поезда пройдут за
5 часов со скоростью сближения 
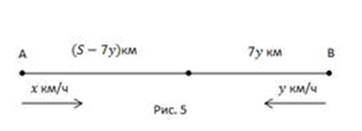
Второй случай: те же условия,
но первый поезд начал движение через 7 часов после второго. За 7 часов второй
поезд прошел 7у км, осталось (700-7у) км, и только тогда начинает движение
первый поезд. Начинается сближение. Поездам нужно пройти (700-7у) км с общей
скоростью х+у, и они встретятся через 2 часа, т.е. 
Мы получили математическую модель.
Упростим полученные уравнения.
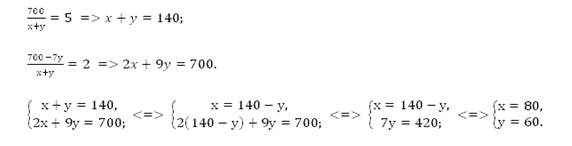
Ответ: 80 км/ч, 60 км/ч.
Задача 2.
Пристани В и С находятся ниже пристани А по течению реки соответственно на 30 км и 45 км. Моторная лодка отходит от пристани А, доходит до С, сразу поворачивает назад и приходит в В, затратив на весь путь 4 часа 40 минут. В другой раз эта же лодка отошла от пристани, дошла до А, сразу повернула назад и пришла в В, затратив на весь путь 7 часов. Чему равна собственная скорость лодки и скорость течения реки?
Решение:
Пусть x км/ч – собственная скорость лодки, y км/ч – скорость течения реки.
Время движения переведем в
часы, 4 часа 40 минут = 
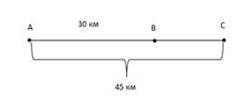
Опишем первый рейс: 
Из А в С лодка шла 45 км по
течению со скоростью х+у км/ч, время в пути составило 
Из С в В лодка шла 15 км
против течения, т.е. 
Из А в В шла 30 км по течению, т.е. 
Опишем второй рейс: 
Из С в А лодка шла 45 км
против течения, т.е. была в пути 
ч. Из А в В шла 30 км по течению, т.е. была в пути 
ч.
Общее время составило 7ч,
т.е. 
Решаем полученную систему: 
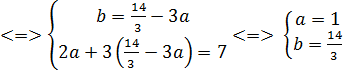
Переходим к старым переменным:
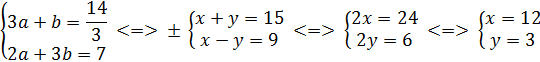
Ответ: 12 км/ч, 3 км/ч.
Задача 6
Гипотенуза прямоугольного треугольника равна 13 см, а его площадь 30 см2. Найти катеты
Решение: Пусть катеты равны х
и у сантиметрам. Используя теорему Пифагора и формулу площади прямоугольного
треугольника, условие задачи запишем так:
Прибавляя к первому уравнению системы второе, умноженное на 4, получаем:
Положительные числа, то х+у= 17. Из этого уравнения выразим у через х и подставим в одно из уравнений системы, например во второе:
Решим полученное уравнение:
17х- 
Список используемой литературы
1. Болтянский В.Г. и др. Симметрия в алгебре. - М.: Наука, 2007.
2. Башмаков М.И. Уравнения и неравенства. - М.: Наука, 2001.
3. Березин В.Н. и др. Сборник задач для факультативных и внеклассных занятий по математике. Книга для учителя. - М.: Просвещение, 2015.
4. Вавилов В.В. и др. Задачи по математике. Алгебра. - М.: Наука, 2007.
5. Черкасов О.Ю. и др. Математика: Справочник для старшеклассников и поступающих в вузы. - М.: АСТ-Пресс, 2016.
6. https://may.alleng.org/d/math/math448.htm
7. https://www.ozon.ru/context/detail/id/1303190/
8. http://scask.ru/g_book_mav.php?id=87
9. Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
![\[A=\left( \begin{matrix} 1 & * & -1 \\ 2 & 5 & * \\ * & -4 & -7 \\ \end{matrix} \right)\]](https://fs.znanio.ru/8c0997/f7/48/cd1eaa1e18a02a7023912f71d3d6ff8c89.png)
