Система счисления

Система счисления — это совокупность приемов и правил, по которым чис­ла записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах вес цифры (т.е. тот вклад, кото­рый она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен десяти.

В позиционных системах счисления вес каждой цифры изменя­ется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в десятичном числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы. Сама же запись числа 757,7 означает со­кращенную запись суммы 700 + 50 + 7 + 0,7 = 7 • 10² + 5 • 10¹ + + 7▪10⁰ + 7▪10 ^-1 = 757,7.

Любая позиционная система счисления характеризуется сво­им основанием.

Основание    позиционной    системы счисления — это количество различных цифр, используемых для изображения чисел в данной системе счисления.

Приняв за основание число 10, получим хорошо знакомую десятичную систему. Число 60 является основанием древней вави­лонской шестидесятеричной системы, к которой восходит деление часа на 60 минут и угла на 360 градусов. Традицию считать дюжи­нами — в году двенадцать месяцев, в сутках два периода по 12 ча­сов, в футе 12 дюймов - распространили англосаксы. В Китае ши­роко использовалась пятеричная система.

За основание системы можно принять любое натуральное число — два, три, четыре и т. д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четве­ричная и т. д.

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения a _n-1 q ^{n -1} + a _n-2 q ^n-2+ ... + a₁ q₁ + a₀q⁰ + a _-1 q ^-1 + ... + a _–m q ^-m, где а_i - цифры системы счисления; n и m - число целых и дробных разрядов соответственно.

ПРИМЕРЫ:

1)Разряды      3210  -1

     Число        1011,   1₂ =  1 • 2³ + 0 • 2² + 1 • 2¹ + 1 • 2° + 1 • 2 ^-1 ;

2)Разряды      210   -1-2

     Число        276,   5 2₈   = 2 • 8² + 7 • 8¹ + 6 • 8° + 5 • 8 ^-1 + 2 • 8 ^-2.

В каждой системе счисления цифры упорядочены в соответ­ствии с их значениями: 1 больше 0, 2 больше 1 и т. д. Продвижени­ем цифры называют замену ее следующей по величине. Продвинуть цифру 1 — значит заменить ее на 2, продвинуть цифру 2 — значит заменить ее на 3 и т. д. Продвижение старшей цифры (например, циф­ры 9 в десятичной системе) означает замену ее на 0. В двоичной си­стеме, использующей только две цифры — 0 и 1, продвижение 0 оз­начает замену его на 1, а продвижение 1 — замену ее на 0. Целые числа в любой системе счисления порождаются с помощью Правила Счета: для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую сле­ва от нее.

Применяя это правило, запишем первые десять целых чисел:

·         в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;    

·         в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

·         в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

·         в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

Кроме десятичной, широко используются системы с основа­нием, являющимся целой степенью числа 2, а именно: т     двоичная (используются цифры  0, 1);

·         восьмеричная    (используются цифры  0, 1, ..., 7);

·         шестнадцатиричная    (для первых целых чисел используются цифры 0, 1, ..., 9,   а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы А, В, С, D, E, F).

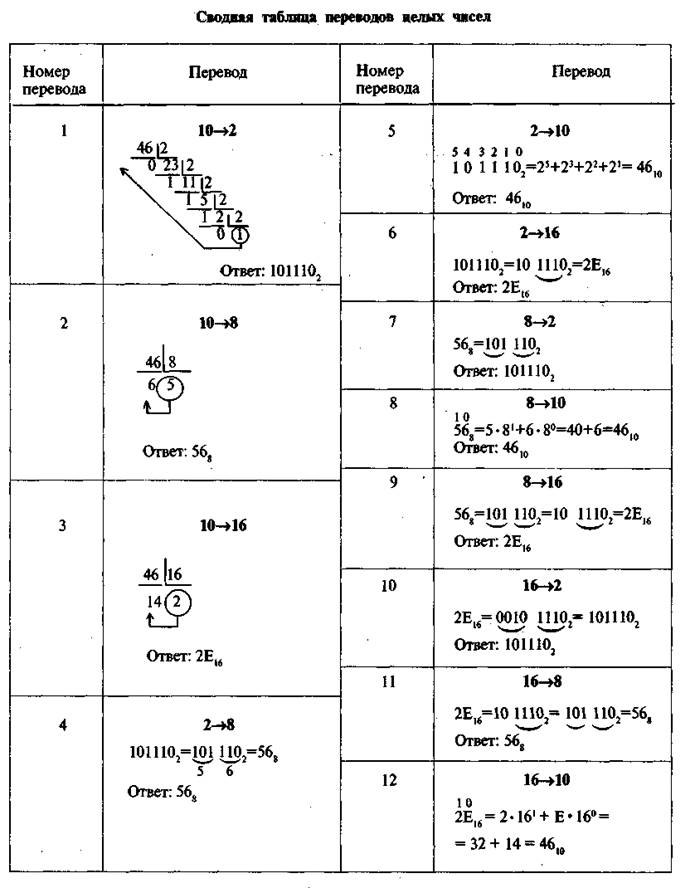
Как перевести число из двоичной  (восьмеричной, шестнадцатеричной) системы в десятичную:

Перевод в десятичную систему числа х, записанного в q-ичной системе счисления (q = 2, 8 или 16) в виде х _q = (a _n a _n-1...а ₀,а _-] а _-2...а _-m) _q, сводится к вычислению значения многочлена х₁₀= a _nq ⁿ + a _n-1 q ^n-1 + ... + a₀q° + a _-1q ^-l + a _-2q ^{-2 +} + ... + a _–m q ^-m средствами десятичной арифметики.

ПРИМЕРЫ:

1)     Разряды    3   2   1   0  -1

    Число            1   0   1   1, 1₂ = 1▪2³+ 1▪2¹ + 1▪2° + 1▪2 ^-1 = 11,5₁₀.

2)     Разряды    2  1  0  -1

    Число            2  7  6, 5₈ = 2▪8² + 7▪8¹ + 6▪8° + 5▪8 ^-1 = 190,625 ₁₀.

3)     Разряды    2  1   0

   Число             1  F  3₁₆ = 1▪6² + 15▪16¹ + 3▪16⁰ = 499₁₀.