
системы линейных уравнений с двумя переменными
Цели: продолжить формирование умения решать графически системы линейных уравнений с двумя переменными; рассмотреть вопрос о возможном количестве решений таких систем; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Является ли пара чисел (2; –5) решением уравнения:
а) 2x + y = 9; в) –x + y = 3;
б) x – y = 7; г) y – 2x = –9?
2. Является ли пара чисел (1; 2) решением системы уравнений:
а) 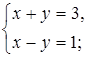 б)
б) 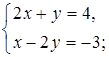 в)
в) 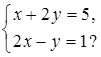
II. Объяснение нового материала.
1) Если угловые коэффициенты прямых различны, то они пересекаются в одной точке, следовательно, система имеет единственное решение.
2) Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые параллельны, следовательно, система не имеет решений.
3) Если уравнения прямых одинаковы, то их графики совпадают, следовательно, система имеет бесконечно много решений.
III. Формирование умений и навыков.
1. Решите графически
систему уравнений: 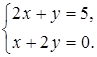
2. № 1062.
Решение:
а) 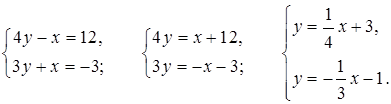
![]() , значит, система имеет одно решение.
, значит, система имеет одно решение.
в) 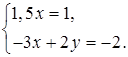
|
1,5x = 1 – прямая, параллельная оси y –3x + 2y = –2 – прямая, непараллельная оси y |
Þ |
система имеет |
г) 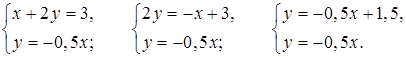
|
–0,5 = –0,5 1,5 ¹ 0 |
Þ система не имеет решений. |
3. № 1064 (а).
4. Подберите, если возможно, такое значение k, при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений.
а) 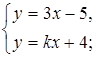 б)
б) 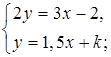 в)
в) 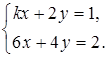
Решение:
а) 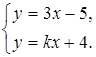
Если k = 3, то прямые будут параллельны, то есть система не будет иметь решений. В остальных случаях прямые пересекаются, значит, система имеет единственное решение.
б) 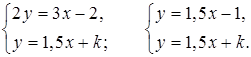
Поскольку коэффициенты при х равны, то прямые будут либо параллельны, либо совпадать, то есть единственное решение система иметь не может.
Если k = –1, то прямые совпадают, значит, система будет иметь бесконечное множество решений. В остальных случаях прямые будут параллельны, то есть система не имеет решений.
в) 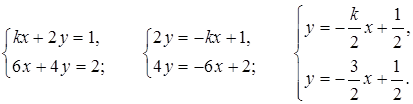
Если ![]() , то есть k = 3, то уравнения
системы будут одинаковы, значит, прямые совпадают, то есть система имеет
бесконечное множество решений. В остальных случаях система будет иметь
единственное решение.
, то есть k = 3, то уравнения
системы будут одинаковы, значит, прямые совпадают, то есть система имеет
бесконечное множество решений. В остальных случаях система будет иметь
единственное решение.
IV. Проверочная работа.
Вариант 1
1. Решите графически
систему уравнений: 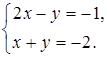
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) 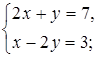 б)
б) 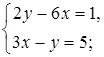 в)
в) 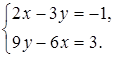
Вариант 2
1. Решите графически
систему уравнений: 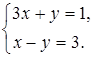
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) 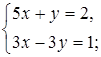 б)
б) 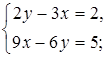 в)
в) 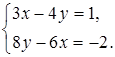
V. Итоги урока.
Домашнее задание: № 1061; № 1063; № 1064 (б).
Вариант 1
1. Решите графически систему уравнений: ![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в)
![]()
Вариант 2
1. Решите графически систему уравнений:![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в) 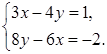
Вариант 1
1. Решите графически систему уравнений: ![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в)
![]()
Вариант 2
1. Решите графически систему уравнений:![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в) 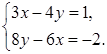
Вариант 1
1. Решите графически систему уравнений: ![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в)
![]()
Вариант 2
1. Решите графически систему уравнений:![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в) 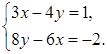
Вариант 1
1. Решите графически систему уравнений: ![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в)
![]()
Вариант 2
1. Решите графически систему уравнений:![]()
2. Не выполняя построений, выясните, сколько решений имеет система уравнений.
а) ![]() б)
б) ![]() в)
в) 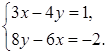
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.