
ЛЕКЦИИ ПО ИНФОРМАТИКЕ
Системы счисления

![]() Тарасова Ирина
Олеговна
Тарасова Ирина
Олеговна
Лекции по информатике
Системы счисления
Методические разработки
для учащихся
Самара, 2019
 |
|||
- так говорили пифагорейцы, подчеркивая необычайно важную роль чисел в практической деятельности.
Еще в самые отдаленные времена людям приходилось считать различные предметы, с которыми они встречались в повседневной жизни. Вначале букв не было. Мысли и слова выражались при помощи рисунков на скалах, на стенах пещер, на камнях. Для запоминания чисел люди пользовались зарубками на деревьях и на палках и узлами на веревках (на рисунке на титульном листе изображен счетовод-казначей, один из коренных жителей Южной Америки (инки), у которого в руках веревочный прибор для узелкового счета). Это и была простейшая и самая древняя – так называемая, унарная система. В ней для записи любых чисел используется всего один символ – палочка, узелок, камушек. Используя именно эту систему счисления, вас научили считать (сами того не осознавая, этим кодом пользуются малыши, показывая на пальцах свой возраст).
 Но с развитием
производства и культуры, когда появилась нужда записывать большие числа, стало
не удобно пользоваться черточками. Тогда стали вводить особые знаки для
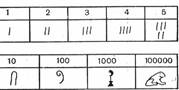
отдельных чисел. Так, например, в Древнем Египте около 4000 лет назад для
обозначения чисел использовали иероглифы, показанные на рисунке.
Но с развитием
производства и культуры, когда появилась нужда записывать большие числа, стало
не удобно пользоваться черточками. Тогда стали вводить особые знаки для
отдельных чисел. Так, например, в Древнем Египте около 4000 лет назад для
обозначения чисел использовали иероглифы, показанные на рисунке.
Единица изображена колом, десяток – как бы парой рук, сотня – свернутым пальмовым листом, тысяча – цветком лотоса, символом изобилия, сто тысяч – лягушкой, так как лягушек было очень много во время разлива Нила.
![]() Так, например число
5736 записывалось следующим образом
Так, например число
5736 записывалось следующим образом
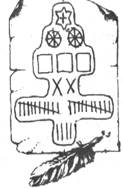
В старину на Руси широко применялись системы счисления, напоминающие систему Древнего Египта. С их помощью сборщики податей заполняли квитанции об уплате подати (ясака) и делали записи в податной тетради. Например, 1232 руб. 24 коп. изображались так как показано на рисунке. Вот текст закона об этих так называемых ясачных знаках: «Чтобы на каждой квитанции кроме изложения словами, было показано особыми знаками число внесенных рублей и копеек так, чтобы сдающие простым счетом сего числа могли быть уверены в справедливости показания. Употребляемые в квитанции знаки означают:
 Звезда
– тысяча рублей
Звезда
– тысяча рублей
Колесо – сто рублей
Квадрат – десять рублей
Х - рубль
| - копейку.
«Дабы неможно было сделать здесь никаких прибавлений, все таковые знаки очерчивать кругом прямыми линиями».
![]()
· запишите свой год рождения при помощи иероглифов Древнего Египта.
· запишите с помощью старинной русской системы счисления сумму 2357 руб. 53 коп
До наших дней сохранилась известная вам римская система счисления. В этой системе цифры обозначаются буквами латинского алфавита:
I = 1 V = 5 X = 10 L = 50
C = 100 D = 500 M = 1000
Для записи промежуточных чисел используется правило: меньшие знаки, поставленные справа от большего, но не более трех одинаковых подряд, прибавляются к его значению, а меньшие знаки, поставленный слева от большего, вычитаются из него, при этом невозможно ставить более одного меньшего слева от большего.
Пример1. Записать число 444 в римской системе.
Решение:
444 = 400 + 40 + 4 = СD + XL + IV = CDXLIV
Пример2. Записать число 2986 в римской системе счисления.
Решение:
2986 = 2000 + 900 + 80 + 6 = MM + CM + LXXX + VI = MMCMLXXXVI.
Пример3. Записать римское число CMLXIII в десятичной системе.
Решение:
CMLXIII=(1000-100) + (50+10) + 3 = 963
Римская система счисления сегодня используется в основном для обозначения знаменательных и юбилейных дат, обозначения веков, разделов и глав в книгах.
![]()
1. Запишите числа в римской системе:
· 2007
· 448
· 1954
2. Запишите числа в десятичной системе:
· MCDXXIII
· LXXIX
· MMCXLI
Из курса математики вам известно, что цифры десятичной записи числа – это просто коэффициенты его представления в виде суммы степеней числа – основания системы счисления:
25076 = 2*10000 + 5*1000 + 0*100 + 7*10 + 6*1 = 2*104 +5*103 + 0*102 +7*101 +6*100
При переводе чисел из десятичной системы счисления в римскую мы и воспользовались этим правилом (444 = 400 + 40 + 4; 2986 = 2000 + 900 + 80 + 6).
При записи чисел значение каждой цифры зависит от ее положения. Место для цифры в числе называется разрядом, а количество цифр в числе разрядностью. На самом деле числа можно записывать как сумму степеней не только числа 10, но и любого другого натурального числа, большего 1.
Определение. Развернутой формой записи числа называется такая запись:а4а3а2а1а0 = а4*q4 + a3*q3 + a2*q2 + a1*q1 + a0*q0 , где а4,а3,а2,а1,а0 –цифры числа, q –основание степени.
Пример4. Получить развернутую форму числа 7512410.
Решение:
а4 = 7, а3 = 5, а2 =1 ,а1 =2, а0 =4, q=10
4 3 2 1 0
![]() 75 12410 = 7*104 + 5*103
+ 1*102 + 2*101 + 4*100.
75 12410 = 7*104 + 5*103
+ 1*102 + 2*101 + 4*100.
Пример5. Получить развернутую форму числа 1123.
Решение:
2 1 0
![]() 1123 = 1*32 + 1*31
+2*30
1123 = 1*32 + 1*31
+2*30
![]()
1. Запишите в развернутом виде числа:
· А8=143511,62
· А2=100111
· А10=143,511
· А16=1А3,5С1
2. Запишите в свернутой форме число:
· 9*101+1*100+5*10-1+3*10-2
· A*162+1*161+C*160+3*16-1
Мы увидели, что есть множество способов представления чисел. В любом случае число изображается группой символов. Будем называть такие символы цифрами, символические изображения чисел – кодами, а правила получения кодов – системами счисления (кодирования).
Определение. Система счисления – это совокупность правил для обозначения и наименования чисел.
Все рассмотренные нами нечисловые системы счисления являются непозиционными.
Определение. Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.
Итак, в непозиционных системах счисления позиция, которую цифра занимает в записи числа, роли не играет. Так, например, римская система счисления непозиционная. В числах XI и IX “вес” обоих цифр одинаков, несмотря на их месторасположение.
Система счисления, которой мы пользуемся в настоящее время, носит название десятичной, так как она основана на счете десятками. Исключительная роль десятка восходит к древнейшим временам и, несомненно, связана со счетом по пальцам на двух руках. Для записи любых чисел в ней используется десять всем хорошо известных цифр (0,1,2,3,4,5,6,7,8,9). Поэтому ее и называют десятичной.
Определение. Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Наименование системы счисления соответствует ее основанию (например, десятичной называется система счисления так потому, что ее основание равно 10, т.е. используется десять цифр).
Давайте рассмотрим число 55. Из двух написанных рядом цифр левая выражает число, в десять раз большее, чем правая. Таким образом, для написания цифр в десятичной системе имеет значение не только сама цифра, но и ее место, позиция. Именно поэтому такую систему счисления называют позиционной.
Определение. Система счисления называется позиционной, если значение цифры зависит от ее места (позиции) в записи числа.
Итак, мы сказали, что в позиционных системах счислениях имеет значение позиция, которую цифра занимает в записи числа. Так, запись 23 означает, что это число можно составить из 3 единиц и 2 десятков. Если мы поменяем позиции цифр, то получим совсем другое число – 32. Это число содержит 3 десятка и 2 единицы. «Вес» двойки уменьшился в десять раз, а «вес» тройки в десять раз возрос.
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, запишем первые несколько целых чисел
В десятичной системе: 0,1,2,3,4,5,6,7,8,9,10,11,…,19,20,21,…
в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
В шестнадцатеричной системе: 0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F, 10,11,12,…,1А,1В,..
![]()
1. Запишите первые 35 чисел троичной системы
2. Запишите первые 25 чисел двоичной системы
Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0.
Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.
Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.
Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.
Таблица соответствия систем счисления.
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
А |
|
11 |
1011 |
13 |
В |
|
12 |
1100 |
14 |
С |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
Е |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
|
17 |
10001 |
21 |
11 |
|
… |
… |
… |
… |
|
26 |
11010 |
32 |
1А |
Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
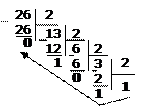 Пример1. Перевести 2610 в двоичную
систему счисления. А10→А2
Пример1. Перевести 2610 в двоичную
систему счисления. А10→А2
Решение:
Ответ: 2610=110102
3 19 18
1
Пример2. Перевести 1910
в троичную систему счисления. А10→А3
![]() Решение:
Решение:
 |
|||
Ответ: 1910=2013
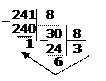 Пример3. Перевести 24110 в
восьмеричную систему счисления. А10→А8
Пример3. Перевести 24110 в
восьмеричную систему счисления. А10→А8
Решение:
Ответ: 24110=3618
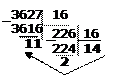 Пример4. Перевести 362710 в
шестнадцатеричную систему счисления. А10→А16
Пример4. Перевести 362710 в
шестнадцатеричную систему счисления. А10→А16
Решение:
Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16.
Ответ: 362710=E2B16
Переведите числа из десятичной системы счисления в другую.
а) 24510→А2 д) 40410→А8
б) 198710→А2 е) 67310→А16
в) 16110→А3 ж) 4534810→А16
г) 33310→А5 з) 44410→А7
Правило перевода дробных чисел из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять умножение исходного числа и получаемых дробные части на q до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.
2. Полученные при таком умножении целые части - числа в системе счисления q – записать в прямом порядке (сверху вниз).
Пример1. Перевести 0,562510 в двоичную систему счисления. А10→А2
![]()
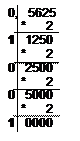 Решение:
Решение:
Ответ: 0,562510=0,10012
Пример2. Перевести 0,562510 восьмеричную систему счисления. А10→А8
![]()
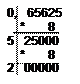 Решение:
Решение:
Ответ: 0,562510=0,528
Пример3. Перевести 0,66510 в двоичную систему счисления. А10→А2
0, 665 * 2 1 330 * 2 0 660 * 2 0 320 * 2 0 640 * 2 1 280 ………….. * 2 0 5000 * 2 1
0000![]()
![]()
Решение:
![]()
![]()
![]() Процесс умножения может
продолжаться до бесконечности. Тогда его прерывают на некотором шаге, когда
считают, что получена требуемая точность представления числа
Процесс умножения может
продолжаться до бесконечности. Тогда его прерывают на некотором шаге, когда
считают, что получена требуемая точность представления числа
Ответ: 0,66510=0,100012
![]()
Переведите числа из десятичной системы счисления в другую.
а) 0, 6562510→А16
б) 0,710→А2 с точностью до 4 знаков после запятой
в) 0,412510→А8 с точностью до 6 знаков
Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляют в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.
Пример1. Перевести 26,2510 в двоичную систему счисления. А10→А2
Решение:
переводим целую часть переводим дробную часть
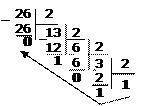 |
|||
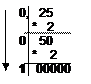 |
|||
Ответ: 26,2510=11010,012
Пример2. Перевести 123,562510 в двоичную систему счисления. А10→А8
Решение:
переводим целую часть переводим дробную часть
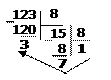
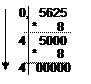
Ответ: 123,562510=173,448
![]()
Перевести из десятичной системы счисления следующие числа:
а) 173,562510→А2
б) 404,6562510→А16
в) 125,2510→А8
Правило Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.
Пример1. Перевести число 1101102 из двоичной системы счисления в десятичную.
Решение:
5 4 3 2 1 0
![]() 1 1 0 1 1 0 2 = 1*25
+ 1*24 + 0*23+1*22+1*21+0*20
=32+16+4+2=5410
1 1 0 1 1 0 2 = 1*25
+ 1*24 + 0*23+1*22+1*21+0*20
=32+16+4+2=5410
Ответ: 1101102 = 5410
Пример2. Перевести число 101,012 из двоичной системы счисления в десятичную.
Решение:
![]() 2 1 0 -1 -2
2 1 0 -1 -2
1 0 1,0 1 2 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510
Ответ: 101,012 = 5,2510
Пример3. Перевести число 1221003 из троичной системы счисления в десятичную.
Решение:
4 3 2 1 0
![]() 1 2 2 0 1 3=1*34 + 2*33
+ 2*32 + 0*31 + 1*30 = 81+54+18+1 = 15410
1 2 2 0 1 3=1*34 + 2*33
+ 2*32 + 0*31 + 1*30 = 81+54+18+1 = 15410
Ответ: 122013 = 15410
Пример4. Перевести число 1637 из семеричной системы счисления в десятичную.
Решение: 1637 = 1*72 + 6*71 + 3*70 = 49+42+3= 9410.
Ответ: 1637 = 9410.
Пример5. Перевести число 234,68 из восьмеричной системы в десятичную:
Решение:
![]() 2 1 0 -1
2 1 0 -1
2 3 4, 68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Ответ: 234,68 = 156,7510.
Пример6. Перевести число 2Е16 в десятичную систему счисления.
Решение:
![]() 2 1
2 1
2 Е16 = 2*161 +14*160 = 32 +14 = 4610.
Ответ: 2Е16 = 4610.
![]()
Перевести из различных систем счисления в десятичную:
а) 1111001112 г) 367,28
б) 1001110,112 в) АВ2Е,816
Перевод целых чисел.
Правило Чтобы перевести целое двоичное число в восьмеричную (8=23) систему счисления необходимо:
· разбить данное число справа налево на группы по 3 цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления.
Пример1. Перевести число 111010102 в восьмеричную систему счисления.
Решение:
![]()
![]() 11101010
11101010
3 5 2
![]() Ответ: 111010102 = 3528
Ответ: 111010102 = 3528
Пример2. Перевести число 111100000101102 в восьмеричную систему счисления.
Решение:
![]()
![]()
![]()
![]() 111110000010110
111110000010110
7 6 0 2 6
![]() Ответ: 111100000101102= 760268
Ответ: 111100000101102= 760268
Правило Чтобы перевести целое двоичное число в шестнадцатеричную (16=24) систему счисления необходимо:
· разбить данное число справа налево на группы по 4 цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления.
Пример3. Перевести число 111000102 в шестнадцатеричную систему счисления.
Решение:
11100010
Е 2
![]() Ответ: 111000102 = Е216
Ответ: 111000102 = Е216
Пример4. Перевести число 111100000101102 в шестнадцатеричную систему счисления.
Решение:
![]()
![]()
![]() 11110000010110
11110000010110
3 С 1 6
![]() Ответ: 111100000101102= 3С1616
Ответ: 111100000101102= 3С1616
Перевод дробных чисел.
Правило Чтобы перевести дробное двоичное число в восьмеричную (шестнадцатеричную) систему счисления необходимо:
· разбить данное число, начиная от запятой влево целую часть и вправо дробную часть на группы по 3 (4) цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной (шестнадцатеричной)системы счисления.
Пример5. Перевести число 0,101100001112 в шестнадцатеричную систему счисления.
![]() Решение:
Решение:
![]()
![]() 0,10110000111
0,10110000111
В 0 7
![]() Ответ: 0,101100001112 = В0716
Ответ: 0,101100001112 = В0716
Пример6. Перевести число 111100001,01112 в восьмеричную систему счисления.
![]() Решение:
Решение:
![]()
![]()
![]() 111100001,0111
111100001,0111
7 4 1 3 1
![]() Ответ: 111100001,01112= 741,318
Ответ: 111100001,01112= 741,318
Пример7. Перевести число 11101001000,110100102 в шестнадцатеричную систему счисления.
![]() Решение:
Решение:
![]()
![]()
![]() 11101001000,11010010
11101001000,11010010
7 4 8 D 2
Ответ: 11101001000,110100102 = 748,D216
![]()
Перевести числа в восьмеричную и шестнадцатеричную системы счисления:
а) 11010001010112
б) 100000011,0001011102
в) 10010111011101,111010112
г) 111110000000111111111,0000011111000001111101012
Правило Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления.
Пример1. Перевести число 5288 перевести в двоичную систему счисления.
![]()
![]() Решение:
Решение:
5 2 3
101 010 011
![]() Ответ: 5288 = 1010100112
Ответ: 5288 = 1010100112
Пример2. Перевести число 4ВА35,1С216 перевести в двоичную систему счисления.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Решение:
Решение:
4 В А 3 5 , 1 С 2
100 1011 101000110101 0001 1100 0010
Ответ: 4ВА35,1С216 = 10010111010001101010001 110000102
Перевести числа в двоичную систему счисления
а) 6217,2518 в) 236548
б) А4ВС10А,5Е16 г) АСЕ560В16
№1 Переведите число из римской системы счисления в десятичную:
MCMLXXXIV = ____________10
№2 Переведите число в римскую систему счисления:
1499 = _______________________
№3 Представьте число в развернутой форме:
235428,210 = ____________________________________________
122231014 = ____________________________________________
№4 Переведите числа из десятичной системы счисления в другие:
5610 = _____________2
5610 = _____________5
№5 Переведите числа в десятичную систему счисления:
110110112 = __________________10
12223 = ____________________10
|
Правило
0+0 =0 1+0=1 0+1=1 1+1=10 |
Пример1. Сложить числа 1112 и 102. Решение: 111 + 10 1001 Проверка: 1112 = 710, 102= 210, 10012 =910 7+2=9 Ответ: 10012 |
Пример2. Сложить числа 111112 и 1112
Решение: 11111
+ 111
100110
Проверка: 111112=1*24+1*23+1*22+1*21+1*20=16+8+4+2+1=3110
1112 = 710
1001102=1*25+0+0+1*22+1*21+0=32+4+2=3810
31+7=38
Ответ: 1001102
Пример3. Сложить числа 11112, 10112, 1112.
Решение:
|
1111 + 1011 111 100001 |
(Пояснение: 1+1+1=11, 1 пишем,1 в уме, 1+1+1=11 плюс 1 в уме равно 100, 0 пишем, 0 в следующий разряд,1- через разряд и т.д.) |
Ответ: 1000012
Пример4. Выполните сложение 1111,1012+101,112.
Решение:
|
111,101 + 101,11 1101,011 |
(Пояснение: по правилам математики при сложение дробных чисел запятая записывается под запятой) |
Ответ: 1101,0112
![]()
Выполните действия:
1) 111110011012+11111112 3) 111,11012+101,00112
2) 1010101112+1111102 4) 111,01010112+101011,11112
|
Правило
0-0=0 1-0=1 1-1=0 0-1=1 (занимаем у старшего разряда) |
Пример1. Из числа 10012 вычесть число 1112. Решение: _ 1001 111 10 Проверка: 10012 =9, 1112 = 7, 102 = 2, 9-7=2 Ответ: 102 |
Пример2. Из числа 1000012 вычесть число 1112
Решение: _ 100001
111
11010
Ответ: 110102
Пример3. Выполнить действие 100101,012 – 111,1112
Решение: _ 100101,010
111,111
11101,101
Ответ: 11101,1012
![]()
Выполните действия:
1) 111110011012-11111112
2) 1010101112-1111102
3) 111,11012-101,00112
4) 101011,11112 - 111,01010112
Умножение в двоичной системе счисления производится аналогично умножению в десятичной системе счисления.
Пример1. Умножить число 1012 на 1102
Решение: 101
*110
000
+ 101
101 .
11110 Ответ: 111102
Пример2. Выполнить действие 1011,012 ∙ 111,112
Решение: 1011,01
* 111,11
101101
101101
+ 101101
101101
101101 ,
1010111,0011
Ответ: 1010111,00112
![]()
Выполните действия:
1) 111110011012-11111112
2) 111,11012-101,00112
Операция деления выполняется также как и в десятичной системе счисления.
Пример1. Разделить число 1010001012 на число 11012.
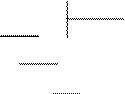 Решение:
Решение:
101000101 1101
1101 11001
1110
1101
1101
1101
0 Ответ: 110012
Пример2. Выполните деление с точностью до 3 знаков после запятой 10012:112
![]() Решение:
Решение:
![]() 1011 11
1011 11
11 . 11,010
101
11
100
11
![]() 101
101
11
10 Ответ: 11,0102
![]()
Выполните действия:
1) 1011110011012:1101012
2) Выполните деление с точностью до 4 знаков после запятой 10012:1012
Используя таблицу и привычные правила сложения, совсем не трудно складывать и вычитать числа в восьмеричной системе счисления
|
Правило
|
Пример1. Вычислите 6348+2758 Решение: 634 + 275 1131 Ответ: 11318
Пример2. Вычислите 305,48+24,758 Решение: 305,4 + 24,75 332,35 Ответ: 332,358 |
Пример3. Вычислите 6348-2758
|
Решение: 634 - 275 337
Ответ: 3378 |
Пояснение: Т.к. от 4 не отнять 5, то занимаем у следующего разряда (т.к. система восьмеричная то 1 разряд составляет 8 единиц). От 8 -5+4=7 Аналогично, т.к. у тройки одну единицу заняли, то необходимо от 2 отнять 7, поэтому, заняв у следующего разряда, получаем 8-7+2=3 и т.д. |
Пример4. Вычислите 305,48-24,758
Решение:
305,40
- 24,75
260,43 Ответ: 260,438
![]()
Выполните действия:
1) 560378+555728
2) 536,2418+5673,668
3) 50238- 44448
4) 56,328-37,5678
Используя правило умножения и сложения восьмеричных чисел не трудно и перемножать данные числа
|
Правило
|
Пример. Вычислите 638∙27,58 Решение: 27,5 63 1067 2156 , 2264,7
Ответ: 2264,78 |
![]()
Выполните умножение чисел:
1) 560378∙555728
2) 536,2418∙5673,668
Сложение и вычитание осуществляется аналогично таким же действиям в восьмеричной системе счисления
|
Правило
|
Пример. Вычислите E5F616+A0716
E5F6 A07 EFFD Ответ: EFFD 16 |
![]()
Выполните действия:
1) 5BE116+70EF316 4) 7E1F316 - 5BE16
2) EB,5A16+7C,B7416 5) ADDC,1E16 - 789,B516
|
Правило
|
Пример
FFA,3 * D,E DFAEA CFB47 / DDAF,5A |
![]()
Выполните действия:
1) 3ED16∙A0516
2) 5C2,5A16∙3D,9EF16
![]() На Новый год на ёлке
висело 32 игрушки и 11 конфет. Всего 103 предмета. В какой системе счисления
записаны числа?
На Новый год на ёлке
висело 32 игрушки и 11 конфет. Всего 103 предмета. В какой системе счисления
записаны числа?
Решение:
32р = 3*р+2
11р = 1*р+1
103р = 1*р2 +0*р+3
32р + 11р = 103р
3*р+2 + 1*р+1 = 1*р2 +0*р+3
4р+3 =р2 +3
р2 – 4р=0
р(р-4)=0
р1 = 0; р2 = 4.
Так как основание системы счисления не может быть меньше 2, то ответом является число 4.
Ответ: В данном примере использована 4-ичная система счисления.
![]() Вычислите 101112
- 5116 : 338, записав результат в двоичной системе
счисления.
Вычислите 101112
- 5116 : 338, записав результат в двоичной системе
счисления.
Решение:
Привычнее всего производить расчеты в десятичной системе счисления, поэтому сначала переведем все числа в десятичную систему и затем произведем соответствующие вычисления.
101112 = 2310
5116 = 8110
338 = 2710
8110 : 2710 = 310
2310 – 310 = 2010
2010 = 101002
Ответ: 101002
№1 Переведите число из двоичной системы счисления в десятичную:
110110112 = ____________10
№2 Переведите числа из двоичной системы счисления в соответствующие:
11011110112 = ________________________________8
11011110112 = ________________________________16
№3 Переведите числа из соответствующих систем счисления в двоичную:
355728 = _________________________2
А517ВЕ16 = _______________________2
№4 Выполните действия:
1101112 + 111102 = ______________________2
1101112 - 111102 = _______________________2
1101112 * 111102 = _______________________2
№5 Вычислить:
A1CA16:1658 – (1000101002:1210 + 100000112)= _____________2
Выполнить следующие задания:
ü Переведите двоичные числа в восьмеричную систему счисления: 101011011; 100010,011101; 0,000110101
ü Переведите двоичные числа в шестнадцатеричную систему счисления: 111111; 100000111,001110; 0,011011011
ü Переведите восьмеричные числа в двоичную систему счисления: 276; 0,635; 25,024
ü Переведите шестнадцатеричные числа в двоичную систему счисления 1А2С7; 0,3С1; F4A,C1C
ü Переведите числа из шестнадцатеричной системы счисления в восьмеричную: А54; 21E,7F; 0,FD
ü Переведите числа из восьмеричной системы счисления в шестнадцатеричную: 344; 0,7612; 333,222
ü Выполните сложение:
1001001+10101
101101 + 1101101
1110101 + 1001101+111101
11000,11+11010,11
ü Выполните вычитание:
10001000-1110011
11010110-10101110
1111001-1010111
1101100-10110110
ü Выполните умножение:
111010*10010
11100*10110
11010*10110
100001*111,11
ü Выполните деление:
1000000:1110
10111001101:110101
11101001001:111101
100111:1100
ü Выполните действия в восьмеричной системе счисления:
345+502; 46,2*64,4; 312*226; 502,23+612,15
ü Выполните действия в шестнадцатеричной системе счисления:
3ЕА5С+235ВА; 35DB*7A2
ü Вычислите: 41568*110112 – 2АС616: 1100102
ТВОРЧЕСКИЙ УРОВЕНЬ:
ü Восстановите двоичные цифры, на месте которых в приведенных ниже примерах стоит знак «*»:
**0*01**1 + 10111*10**=100*1*00010
***0**00 - 11*11*11=1101*1
1*01 · 1**=101101
ü Подсчитайте сумму всех троичных чисел в диапазоне от 103 до 1123, включая границы диапазона. Ответ запишите в двоичной системе счисления.
ü Какое число необходимо прибавить к числу 1001111011112 чтобы получилось сокращенное английское название дисковода для мягких магнитных дисков. Ответ записать в восьмеричной системе счисления.
ü В нашем классе 110002 учеников. 110010% из них учатся на «хорошо» и «отлично». Сколько учеников учатся на «хорошо» и «отлично»?
В лекциях использованы материалы учебных пособий:
1. Андреева Е., Фалина И. Системы счисления и компьютерная арифметика. Изд. 2-е, - М.: Лаборатория Базовых Знаний, 2000.
2. Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов. – М.: Бином. Лаборатория Знаний, 2002.
Содержание:
§1. О системах счисления.
n1. Немного из истории.
n2. Римская система.
n3. Развернутая форма числа
n4. Основные понятия.
N5. Как порождаются целые числа в позиционных системах счисления?
N6. Системы счисления, используемые в компьютерах.
§2. Перевод чисел из одной системы счисления в другую.
n1. Перевод целых чисел из десятичной системы счисления в другую.
n2. Перевод дробных чисел из десятичной системы счисления в другую.
n3. Перевод произвольных чисел из десятичной системы счисления в другую.
n4. Перевод чисел из любой системы счисления в десятичную.
n5. Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления.
n6. Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления.
§3. Арифметические операции в системах счисления.
n1. Сложение в двоичной системе счисления.
n2. Вычитание в двоичной системе счисления.
n3. Умножение в двоичной системе счисления.
n4. Деление в двоичной системе счисления.
n5. Сложение и вычитание в восьмеричной системе счисления.
n6. Умножение в восьмеричной системе счисления.
n7. Сложение и вычитание в шестнадцатеричной системе счисления.
n8. Умножение в шестнадцатеричной системе счисления.
§4. Нестандартные задачи
Индивидуальная работа учащегося
Литература
![]()
![]()
![]()
![]()
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.