
1 СИСТЕМЫ СЧИСЛЕНИЯ И ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЭВМ
1.1 Понятие об основных системах счисления
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами. Все системы счисления делятся на позиционные и непозиционные.
Непозиционными называются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе. Примером непозиционной системы счисления является римская система, в которой символам I, V, X, L, С, D, М соответствуют числа 1, 5, 10, 50, 100, 500, 1000. Недостатком этой системы является сложность формальных правил записи чисел и выполнения арифметических действий над ними.
Система счисления называется позиционной, если значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Это значение находится в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество различных цифр, употребляемых в позиционной системе, определяет название системы счисления и называется основанием системы счисления. Так, в десятичной системе используются десять цифр (от 0 до 9), основанием этой системы является число десять.
В позиционных системах счисления числа записываются в виде последовательности символов:
N = an an-1 ... a1 a0 , a-1 a-2 ... а-m (р) (1)
где N – число; ai – цифры (символы) числа;
p – основание системы счисления;
n, m – порядковый номер разряда для целой (n) и дробной (m) частей числа соответственно.
В этой последовательности запятая отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Значение числа, записанного в виде (1), может быть найдено по следующей формуле:
N = an·pn+an-1·pn-1+ ... +a0·p0+a-1·p-1+a-2·p-2+ ...+а-m·p-m . (2)
В десятичной системе счисления мы производим вычисления по формуле (2) практически не задумываясь. Возьмём для примера десятичное число 123,45:
2 1 0 -1 -2
123,45 (10) = 1·102+2·101+3·100+4·10-1+5·10-2 = 100+20+3+0,4+0,05
Здесь и в дальнейшем основание системы счисления, в которой представлено число, будем указывать в виде нижнего индекса в скобках.
Помимо десятичной, в ЭВМ применяются и другие позиционные системы счисления: двоичная, восьмеричная, шестнадцатеричная. Двоичная система счисления.
Используется две цифры: 0 и 1. Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным кодом. Примеры представления чисел в двоичной системе счисления представлены в таблице 1. Восьмеричная система счисления.
Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употреблялась в ЭВМ первого и второго поколений как вспомогательная для записи адресов и данных в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1). Триада получается путем добавления, при необходимости, незначащих нулей. Шестнадцатеричная система счисления.
Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр - латинскими буквами: 10-A, 11-B, 12-C, 13-D, 14-E, 15-F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада, или полубайт) (Таблица 1).
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
000 |
0 |
0000 |
|
1 |
I |
1 |
1 |
001 |
1 |
0001 |
|
2 |
II |
10 |
2 |
010 |
2 |
0010 |
|
3 |
III |
11 |
3 |
011 |
3 |
0011 |
|
4 |
IV |
100 |
4 |
100 |
4 |
0100 |
|
5 |
V |
101 |
5 |
101 |
5 |
0101 |
|
6 |
VI |
110 |
6 |
110 |
6 |
0110 |
|
7 |
VII |
111 |
7 |
111 |
7 |
0111 |
|
8 |
VIII |
1000 |
10 |
001 000 |
8 |
1000 |
|
9 |
IX |
1001 |
11 |
001 001 |
9 |
1001 |
|
10 |
X |
1010 |
12 |
001 010 |
A |
1010 |
|
11 |
XI |
1011 |
13 |
001 011 |
B |
1011 |
|
12 |
XII |
1100 |
14 |
001 100 |
C |
1100 |
|
13 |
XIII |
1101 |
15 |
001 101 |
D |
1101 |
|
14 |
XIV |
1110 |
16 |
001 110 |
E |
1110 |
|
15 |
XV |
1111 |
17 |
001 111 |
F |
1111 |
|
16 |
XVI |
10000 |
20 |
010 000 |
10 |
0001 0000 |
|
17 |
XVII |
10001 |
21 |
010 001 |
11 |
0001 0001 |
1.2 Перевод чисел из одной системы счисления в другую Перевод чисел в десятичную систему осуществляется путем составления степенного ряда (2) с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
а) Перевести 10101101,101(2) в десятичную систему счисления
10101101,101(2) = 1·27 + 0·26 + 1·25 + 0·24 + 1·23 + 1·22 + 0·21 + 1·20 + 1·2-1
+ + 0·2-2 + 1·2-3 = 173,625(10)
б) Перевести 703,04(8) в десятичную систему счисления 703,04(8) = 7·82 + 0·81 + 3·80+ 0·8-1 + 4·8-2 = 451,0625(10)
в) Перевести B2E,4(16) в десятичную систему счисления B2E,4(16) = 11·162 + 2·161 + 14·160 + 4·16-1 = 2862,25(10)
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное, меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести 181(10) в восьмеричную систему счисления
_181 8
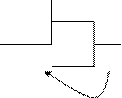 176 _22
8
176 _22
8
5 16 2
6
Результат: 181(10) = 265(8)
б) Перевести 622(10) в шестнадцатеричную систему счисления
_622 16
48 _38 16
_142 32 2
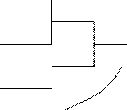 128
6
128
6
14
Результат: 622(10) = 26E(16)
Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 0,3125(10) в восьмеричную систему счисления
0 , 3125 × 8
|
|
|
Результат: 0,3125(10) = 0,24(8)
Замечание. Конечной десятичной дроби может соответствовать бесконечная (периодическая) дробь в недесятичной системе счисления. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 0,65(10) в двоичную систему счисления с точностью до 6 зна-
ков после запятой.
0, 65 × 2
|
|
|
...
Результат: 0,65(10) ≈ 0,101001 (2)
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример.
Перевести 23,125(10) в двоичную систему счисления
1) Переведем целую часть:
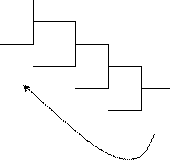 _ 23 2 22
_11 2 1 10 _5 2
_ 23 2 22
_11 2 1 10 _5 2
1 4 _2 2
1 2 1
2) Переведем дробную часть:
0, 125 × 2
|
|
|
Таким образом: 0,125(10) = 0,001(2); 23(10) = 101112. Результат: 23,125(10) = 10111,001(2).
Необходимо отметить, что целые числа остаются целыми, а правильные
дроби - дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) – для восьмеричной системы счисления или четырехразрядным двоичным числом (тетрадой) – для шестнадцатеричной системы счисления (таблица 1), после чего отбрасывают незначащие нули в старших и младших разрядах.
Пример.
а) Перевести 305,4(8) в двоичную систему счисления
3 0 5 , 4 (8)
![]() 011 000
101 100 = 11000101,1(2)
011 000
101 100 = 11000101,1(2)
б) Перевести 7B2,E(16) в двоичную систему счисления
7 В 2 , Е (16)
![]() 0111
1011 0010 1110 = 11110110010,111(2)
0111
1011 0010 1110 = 11110110010,111(2)
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от десятичной точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой (таблица 1).
Пример.
а) Перевести 1101111001,1101(2) в восьмеричную систему счисления
![]() 001 101 111 001
, 110 100 = 1571,64(8)
001 101 111 001
, 110 100 = 1571,64(8)
1 5 7 1 6 4
б) Перевести 11111111011,100111(2) в шестнадцатеричную систему счисления
![]() 0111
1111 1011 , 1001 1100 = 7FB,9C(16)
0111
1111 1011 , 1001 1100 = 7FB,9C(16)
7 F B 9 С
Перевод из восьмеричной в шестнадцатеричную систему и обратно удобно осуществлять через двоичную систему с помощью триад и тетрад.
Пример.
Перевести 175,24(8) в шестнадцатеричную систему счисления
![]() 001
111 101 010 100 7
D 5
001
111 101 010 100 7
D 5
1.3 Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами такие же, как и в десятичной системе, и задаются таблицами двоичного сложения, вычитания и умножения (таблица 2). Подобные таблицы для восьмеричной и шестнадцатеричной систем счисления приведены в Приложении.
Таблица 2 - Арифметические действия над двоичными числами
|
Таблица двоичного сложения |
Таблица двоичного вычитания |
Таблица двоичного умножения |
|
0+0=0 0+1=1 1+0=1 1+1=10 |
0-0=0 1-0=1 1-1=0 10-1=1 |
0×0=0 0×1=0 1×0=0 1×1=1 |
При сложении двоичных чисел производится сложение цифр слагаемых в каждом разряде и единиц переноса из соседнего младшего разряда, если они имеются. При этом необходимо учитывать, что в двоичной системе переполнение разряда наступает при количестве единиц, больше либо равным двум. В случае переполнения нужно вычесть из текущего разряда число, равное основанию системы (в данном случае – два), и добавить единицу переноса в следующий старший разряд.
Прежде чем рассматривать приведенные ниже примеры, полезно попробовать получить для различных систем счисления порядковые последовательности путём прибавления единицы к предыдущему числу, начиная с нуля, а затем сравнить их с соответствующими столбцами таблицы 1. Затем попробуйте получить последовательности путём вычитания в обратном порядке.
Пример.
Выполнить сложение двоичных чисел (X, Y, Z):
а) X=1101, Y=101;
единицы переноса
![]()
1 1 1 1 0 1
+
1 0 1
1 0 0 1 0
Результат: 1101+101=10010.
б) X=1101, Y=101, Z=111;
1
1 1 1
1 1 0 1
+
1 0 1
+
1 1 1
1 1 0 0 1
Результат: 1101+101+111=11001.
При вычитании двоичных чисел, аналогично вычитанию десятичных, может возникнуть необходимость займа единицы из предыдущего старшего разряда. Эта занимаемая единица переносится в текущий разряд как двойка (количество единиц, равное основанию).
Пример.
Заданы двоичные числа X=10010 и Y=101. Вычислить X - Y.
. . .
_1 0 0 1 0
0
![]() 1 1 0 1
1 1 0 1
Результат 10010 - 101=1101.
Умножение двоичных чисел оказывается гораздо проще десятичных и
сводится к операциям сдвига и сложения.
Пример. Заданы двоичные числа X=1001 и Y=101. Вычислить X × Y.
1 0 0 1
1 0 0 1
![]() 1
0 0 1
1
0 0 1
1 0 1 1 0 1
Результат: 1001×101=101101.
Выполнение деления в двоичной системе также проще, чем в десятич-
ной, и сводится к операциям сравнения, сдвига и вычитания.
Пример.
Заданы двоичные числа X=1100,011 и Y=10,01. Вычислить X : Y
_ 1 1 0 0 0 1, 1 1 0 0 1
![]() 1
0 0 1 1 0 1, 1
1
0 0 1 1 0 1, 1
1 0 0 1 _ 1 0 0 1 1 0 0 1
Результат. 1100,011 : 10,01=101,1.
1.4 Представление чисел в ЭВМ
В цифровых ЭВМ числовая информация представляется в двух формах:
- с фиксированной точкой (естественная форма);
- с плавающей точкой (экспоненциальная форма).
При представлении чисел с фиксированной точкой подразумевается, что положение точки, разделяющей число на целую и дробную части, неизменно для всех чисел. Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. В современных ЭВМ естественная форма используется, например, для представления целых чисел (дробная часть числа всегда отсутствует), денежных сумм (дробная часть всегда составляет четыре знака).
Представление с плавающей точкой любого числа N в общем виде опи-
сывается следующей формулой:
N = ± M ⋅ p±k, (3)
где ±M – мантисса (дробная часть) числа; p – основание системы счисления;
±k – порядок (целое число),
при этом положительный знак мантиссы и порядка может опускаться, а при указании порядка в десятичной системе принято использовать символ Е. Например, десятичное число с фиксированной точкой 123,45 может быть представлено в форме с плавающей точкой как 0,12345 ⋅ 103, или, как это принято, 1.2345Е+02.
Такая форма представления имеет огромный диапазон отображения чисел и является основной в современных ЭВМ.
Исходные данные в ЭВМ хранятся в виде двоичных чисел, то есть записываются в виде последовательности нулей и единиц. В памяти ЭВМ одна двоичная цифра записывается в один двоичный разряд, называемый битом. За единицу представления данных в цифровых ЭВМ принят байт – восемь бит, поэтому число разрядов ячеек памяти всегда кратно восьми, а данные имеют байтовую структуру, то есть состоят из определенного числа байтов.
Более крупные единицы измерения данных образуются добавлением
префиксов кило-, мега-, гига-, тера-:
1 килобайт (Кбайт) = 210 байт = 1024 байт
1 мегабайт (Мбайт) = 220 байт = 1024 Кбайт
1 гигабайт (Гбайт) = 230 байт = 1024 Мбайт
1 терабайт (Тбайт) = 240 байт = 1024 Гбайт
Для представления положительных и отрицательных чисел в машинах используются специальные коды: прямой, обратный и дополнительный. Причем два последних позволяют заменить неудобную для ЭВМ операцию вычитания на операцию сложения с отрицательным числом; дополнительный код обеспечивает более быстрое выполнение операций при помощи сумматора, поэтому в ЭВМ применяется чаще именно он. Рассмотрим правила кодирования на примере целых чисел.
Для перевода числа в прямой код знак числа опускается, а в старший (знаковый) разряд ставится 0, если число положительное, и 1 – если число отрицательное. Младшие разряды кода являются двоичным представлением модуля числа. Оставшиеся разряды кода заполняются нулями. Отметим, что перевод положительных чисел в прямой, обратный и дополнительный код не изменяет изображения этих чисел (таблица 3).
Для перевода отрицательного числа в обратный код необходимо все, кроме знакового, разряды прямого кода проинвертировать (заменить нули на единицы, а единицы на нули).
Для перевода отрицательного числа в дополнительный код необходимо к младшему разряду его обратного кода прибавить единицу.
Перевод отрицательного числа из дополнительного кода в прямой осуществляется в обратной последовательности: сначала вычитается единица, затем инвертируются разряды. Напоминаем, что положительное число (0 в старшем разряде) обратному переводу не подвергается, поскольку имеет одинаковую запись как в прямом коде, так и в дополнительном.
Таблица 3 – Примеры представления целых чисел в шестнадцатиразрядных двоичных кодах
|
Число |
прямой код |
обратный код |
дополнительный код |
|
0 |
0000 0000 0000 0000 |
0000 0000 0000 0000 |
0000 0000 0000 0000 |
|
1 |
0000 0000 0000 0001 |
0000 0000 0000 0001 |
0000 0000 0000 0001 |
|
-1 |
1000 0000 0000 0001 |
1111 1111 1111 1110 |
1111 1111 1111 1111 |
|
20 |
0000 0000 0001 0100 |
0000 0000 0001 0100 |
0000 0000 0001 0100 |
|
-20 |
1000 0000 0001 0100 |
1111 1111 1110 1011 |
1111 1111 1110 1100 |
При написании программ важно определить диапазоны значений и формы представления обрабатываемой информации. Например, в языках программирования семейства BASIC (Бейсик) типы переменных INTEGER и LONG используются, соответственно, для хранения целых чисел со знаком в шестнадцатиразрядном (два байта, или полуслово) и тридцатидвухразрядном (четыре байта, или машинное слово) дополнительном коде. Знак числа фиксируется в нулевом бите первого байта (крайний левый бит). Цифровая часть числа хранится в остальных битах поля числа, причем младший двоичный разряд числа находится в последнем, правом бите последнего байта. Переменные типа SINGLE и DOUBLE используются для хранения чисел с плавающей точкой в четырех или восьми байтах (двойное слово) соответственно. Знак хранится в нулевом бите, биты 1-7 отводятся под порядок числа, остальные биты используются для разрядов мантиссы. Как правило, мантисса хранится в нормальном виде, то есть первым ее разрядом не является 0.
1.5 Кодирование информации в ЭВМ
Для представления символьной информации в двоичной форме используются таблицы кодировки. При длине кода один байт (8 бит) можно закодировать 256 (то есть 28) различных символов. Этого достаточно для кодирования символов любого национального алфавита, но недостаточно, чтобы представить в одной таблице символы всех алфавитов. Уровня международного стандарта достигла система ASCII (American Standard Code for Information Interchange —
Американский стандартный код для обмена информацией). Эта система устанавливает две таблицы кодирования: базовую и расширенную. В базовой таблице закреплены значения кодов от 0 до 127. Первые 32 кода являются управляющими, они предназначены для управления устройствами вывода данных и определяются производителями. Большинство значений кодов базовой таблицы ASCII представлено в Приложении.
Расширенная таблица определяет значения кодов со 128 по 255 и используется национальными системами кодирования. Например, в России наибольшее распространение получили три разных системы: ГОСТ-альтернативная (на компьютерах, работающих в операционной системе MS-DOS); Windows-1251; КОИ-8 (код обмена информации, восьмизначный).
В настоящее время всё большее распространение получает универсальная система кодирования (UNICODE). В ней используется шестнадцатиразрядный код, позволяющий представить 65 536 (то есть 216) символов. Этого достаточно для кодирования символов большинства языков планеты. Однако текст в кодировке UNICODE занимает вдвое больший объем в памяти ЭВМ или на машинном носителе информации, по сравнению с этим же текстом в кодировке ASCII или любой другой восьмиразрядной системе кодирования.
Существует множество способов представления графики, звука, видео, других видов данных и их совокупностей, и оно постоянно расширяется. Таким образом, многообразие систем кодирования ставит одну из важнейших задач информатики – задачу межсистемного преобразования данных.
1.6 Задания к работе
Ц е л ь р а б о т ы . Изучение систем счисления, используемых в вычислительной технике и правил перевода чисел из одной системы счисления в другую.
З а д а н и е к р а б о т е с о с т о и т и з ч е т ы р ё х п у н к т о в .
1. Перевести данные числа в десятичную систему счисления.
2. Перевести данные числа из десятичной системы счисления в двоич-ную, восьмеричную и шестнадцатеричную системы счисления (с точностью 6 знаков после запятой). Выполнить проверку путем обратного перевода в десятичную систему счисления.
3. Сложить числа в указанной системе счисления.
4. Выполнить вычитание в указанной системе счисления.
1. а) 10100010(2); б) 1110010111(2); в) 110010010,101(2);
г) 1111011100,10011(2); д) 605,02(8); е) 3C8,8(16).
2. а) 969(10); б) 549(10); в) 973,375(10); г) 508,5(10); д) 281,09(10).
3. а) 1111010100(2)+10000000010(2); б) 101001011(2)+10000000010(2);
в) 1011101001,1(2)+1110111,01(2); г) 1053,34(8)+1513,2(8); д) 40A,E8(16)+92,7(16).
4. а) 1001100011(2)-111111110(2); б) 1110001000(2)-1011110(2);
в) 10000010111,001(2)-1000010,01(2); г) 553,2(8)-105,5(8); д) 298,9(16)-67,4(16). Вариант 2
1. а) 1100111011(2); б) 10000000111(2); в) 10110101,1(2);
г) 100000110,10101(2); д) 671,24(8); е) 41A,6(16).
2. а) 666(10); б) 305(10); в) 153,25(10); г) 162,25(10); д) 248,46(10)
3. а) 10000011(2)+1000011(2); б) 1010010000(2)+1101111011(2);
в) 110010,101(2)+1011010011,01(2); г) 356,5(8)+1757,04(8); д) 293,8(16)+3CC,98(16).
4. а) 100111001(2)-110110(2); б) 1111001110(2)-111011010(2);
в) 1101111011,01(2)-101000010,0111(2); г) 2025,2(8)-131,2(8); д) 2D8,4(16)-A3,B(16). Вариант 3
1. а) 1100000000(2); б) 1101011111(2); в) 1011001101,00011(2);
г) 1011110100,011(2); д) 1017,2(8); е) 111,B(16).
2. а) 273(10); б) 661(10); в) 156,25(10); г) 797,5(10); д) 53,74(10)
3. а) 1110001000(2)+110100100(2); б) 1001001101(2)+1111000(2);
в) 111100010,0101(2)+1111111,01(2); г) 573,04(8)+1577,2(8); д) 108,8(16)+21B,9(16).
4. а) 1010111001(2)-1010001011(2); б) 1110101011(2)-100111000(2);
в) 1110111000,011(2)-111001101,001(2); г) 1300,3(8)-464,2(8); д) 37C,4(16)-1D0,2(16). Вариант 4
1. а) 1100001001(2); б) 1100100101(2); в) 1111110110,01(2);
г) 11001100,011(2); д) 112,04(8); е) 334,A(16).
2. а) 105(10); б) 358(10); в) 377,5(10); г) 247,25(10); д) 87,27(10)
3. а) 101000011(2)+110101010(2); б) 111010010(2)+1011011110(2);
в) 10011011,011(2)+1111100001,0011(2); г) 1364,44(8)+1040,2(8); д) 158,A(16)+34,C(16).
4. а) 1111111000(2)-100010011(2); б) 1111101110(2)-11100110(2);
в) 1001100100,01(2)-10101001,1(2); г) 1405,3(8)-346,5(8); д) 3DD,4(16)-303,A(16). Вариант 5
1. а) 1101010001(2); б) 100011100(2); в) 1101110001,011011(2);
г) 110011000,111001(2); д) 1347,17(8); е) 155,6C(16).
2. а) 500(10); б) 675(10); в) 810,25(10); г) 1017,25(10); д) 123,72(10)
3. а) 1000101101(2)+1100000010(2); б) 1111011010(2)+111001100(2);
в) 1001000011,1(2)+10001101,101(2); г) 415,24(8)+1345,04(8); д) 113,B(16)+65,8(16).
4. а) 1101111100(2)-100100010(2); б) 1011010110(2)-1011001110(2);
в) 1111011110,1101(2)-1001110111,1(2); г) 1333,2(8)-643,2(8); д) 176,7(16)-E5,4(16). Вариант 6
1. а) 111000100(2); б) 1011001101(2); в) 10110011,01(2);
г) 1010111111,011(2); д) 1665,3(8); е) FA,7(16).
2. а) 218(10); б) 808(10); в) 176,25(10); г) 284,25(10); д) 253,04(10)
3. а) 11100000(2)+1100000000(2); б) 110101101(2)+111111110(2);
в) 10011011,011(2)+1110110100,01(2); г) 1041,2(8)+1141,1(8); д) 3C6,8(16)+B7,5(16).
4. а) 10110010(2)-1010001(2); б) 1101000000(2)-10000000(2);
в) 1100101111,1101(2)-100111000,1(2); г) 1621,44(8)-1064,5(8); д) 1AC,B(16)-BD,7(16). Вариант 7
1. а) 1111000111(2); б) 11010101(2); в) 1001111010,010001(2);
г) 1000001111,01(2); д) 465,3(8); е) 252,38(16).
2. а) 306(10); б) 467(10); в) 218,5(10); г) 667,25(10); д) 318,87(10)
3. а) 1000001101(2)+1100101000(2); б) 1010011110(2)+10001000(2);
в) 1100111,00101(2)+101010110,011(2); г) 520,4(8)+635,4(8); д) 2DB,6(16)+15E,6(16).
4. а) 1101000101(2)-111111000(2); б) 11110101(2)-110100(2);
в) 1011101011,001(2)-1011001000,01001(2); г) 1034,4(8)-457,44(8); д) 239,A(16)-9C,4(16). Вариант 8
1. а) 110010001(2); б) 100100000(2); в) 1110011100,111(2);
г) 1010111010,1110111(2); д) 704,6(8); е) 367,38(16).
2. а) 167(10); б) 113(10); в) 607,5(10); г) 828,25(10); д) 314,71(10)
3. а) 10101100(2)+111110010(2); б) 1000000010(2)+110100101(2); в) 1110111010,10011(2)+1011010011,001(2); г) 355,2(8)+562,04(8); д) 1E5,18(16)+3BA,78(16).
4. а) 1010110010(2)-1000000000(2); б) 1111100110(2)-10101111(2);
в) 1101001010,101(2)-1100111000,011(2); г) 1134,54(8)-231,2(8); д) 2DE,6(16)-12A,4(16). Вариант 9
1. а) 1000110110(2); б) 111100001(2); в) 1110010100,1011001(2);
г) 1000000110,00101(2); д) 666,16(8); е) 1C7,68(16).
2. а) 342(10); б) 374(10); в) 164,25(10); г) 520,375(10); д) 97,14(10).
3. а) 1101010000(2)+1011101001(2); б) 100000101(2)+1100001010(2);
в) 1100100001,01001(2)+1110111111,011(2); г) 242,2(8)+1153,5(8); д) 84,8(16)+27E,8(16).
4. а) 1111110(2)-1111011(2); б) 1111100000(2)-111110011(2);
в) 1111011111,1001(2)-1010111100,01(2); г) 1241,34(8)-1124,3(8); д) 15F,A(16)-159,4(16). Вариант 10
1. а) 101111111(2); б) 1111100110(2); в) 10011000,1101011(2);
г) 1110001101,1001(2); д) 140,22(8); е) 1DE,54(16).
2. а) 524(10); б) 222(10); в) 579,5(10); г) 847,625(10); д) 53,35(10).
3. а) 1101010000(2)+11100100(2); б) 100110111(2)+101001000(2);
в) 1111100100,11(2)+1111101000,01(2); г) 1476,3(8)+1011,1(8); д) 3E0,A(16)+135,8(16).
4. а) 1010010100(2)-11101110(2); б) 10000001110(2)-10011100(2);
в) 1110100111,01(2)-110000001,1(2); г) 1542,5(8)-353,24(8); д) 3EB,8(16)-3BA,8(16). Вариант 11
1. а) 11101000(2); б) 1010001111(2); в) 1101101000,01(2);
г) 1000000101,01011(2); д) 1600,14(8); е) 1E9,4(16).
2. а) 113(10); б) 875(10); в) 535,1875(10); г) 649,25(10); д) 6,52(10).
3. а) 1000111110(2)+1011000101(2); б) 1001000(2)+1101101001(2);
в) 110110010,011(2)+1000011111,0001(2); г) 620,2(8)+1453,3(8); д) 348,1(16)+234,4(16).
4. а) 1100001010(2)-10000011(2); б) 1101000001(2)-10000010(2);
в) 110010110,011(2)-10010101,1101(2); г) 1520,5(8)-400,2(8); д) 368,4(16)-239,6(16).
Вариант 12 1. а) 10000011001(2); б) 10101100(2); в) 1101100,01(2); г) 1110001100,1(2); д) 1053,2(8); е) 200,6(16).
2. а) 294(10); б) 723(10); в) 950,25(10); г) 976,625(10); д) 282,73(10).
3. а) 1000111110(2) + 10111111(2); б) 1111001(2) + 110100110(2); в) 1001110101,00011(2) + 1001001000,01(2); г) 104,4(8) + 1310,62(8); д) 2BD,3(16)+EB,C(16).
4. а) 11110111(2)-11110100(2); б) 1001100111(2)-101100111(2);
в) 1100110111,001(2)-1010001101,0011(2); г) 631,1(8)-263,2(8); д) 262,8(16)-1D6,88(16). Вариант 13
1. а) 110111101(2); б) 1110011101(2); в) 111001000,01(2);
г) 1100111001,1001(2); д) 1471,17(8); е) 3EC,5(16).
2. а) 617(10); б) 597(10); в) 412,25(10); г) 545,25(10); д) 84,82(10).
3. а) 1110100100(2)+1010100111(2); б) 1100001100(2)+1010000001(2); в) 1100111101,10101(2) + 1100011100,0011(2); г) 750,16(8) + 1345,34(8); д) 158,4(16)+396,8(16).
4. а) 10000000010(2)-100000001(2); б) 1110111111(2)-1010001(2);
в) 1011001100,1(2)-100100011,01(2); г) 1110,62(8)-210,46(8); д) 1D8,D8(16)-110,4(16). Вариант 14
1. а) 1101100000(2); б) 100001010(2); в) 1011010101,1(2);
г) 1010011111,1101(2); д) 452,63(8); е) 1E7,08(16).
2. а) 1047(10); б) 335(10); в) 814,5(10); г) 518,625(10); д) 198,91(10).
3. а) 1101100101(2)+100010001(2); б) 1100011(2)+110111011(2);
в) 1010101001,01(2)+10011110,11(2); г) 1672,2(8)+266,2(8); д) 18B,A(16)+2E9,2(16).
4. а) 1110111011(2)-100110111(2); б) 1110000101(2)-1001110(2);
в) 1011110100,0011(2)-101001011,001(2); г) 1560,22(8)-1142,2(8); д) 1A5,8(16)-7D,A(16). Вариант 15
1. а) 1001110011(2); б) 1001000(2); в) 1111100111,01(2);
г) 1010001100,101101(2); д) 413,41(8); е) 118,8C(16).
2. а) 164(10); б) 255(10); в) 712,25(10); г) 670,25(10); д) 11,89(10)
3. а) 1100001100(2)+1100011001(2); б) 110010001(2)+1001101(2);
в) 111111111,001(2)+1111111110,0101(2); г) 1443,1(8)+242,44(8); д) 2B4,C(16)+EA,4(16).
4. а) 1001101100(2)-1000010111(2); б) 1010001000(2)-1000110001(2);
в) 1101100110,01(2)-111000010,1011(2); г) 1567,3(8)-1125,5(8); д) 416,3(16)-255,3(16). Вариант 16
1. а) 1010100001(2); б) 10000010101(2); в) 1011110000,100101(2);
г) 1000110001,1011(2); д) 1034,34(8); е) 72,6(16).
2. а) 887(10); б) 233(10); в) 801,5(10); г) 936,3125(10); д) 218,73(10).
3. а) 1010110101(2)+101111001(2); б) 1111100100(2)+100110111(2);
в) 111111101,01(2)+1100111100,01(2); г) 106,14(8)+322,5(8); д) 156,98(16)+D3,2(16).
4. а) 1111100100(2)-110101000(2); б) 1110110100(2)-1101010101(2);
в) 1100001,0101(2)-1011010,101(2); г) 537,24(8)-510,3(8); д) 392,B(16)-149,5(16).
1.7 Пример выполнения работы З а д а н и е
1. Перевести данные числа в десятичную систему счисления:
а) 1110010011,1011(2); б) 772,24(8); в) 81,A(16).
2. Перевести число 119(10) из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. Выполнить проверку путем обратного перевода в десятичную систему счисления.
3. Сложить числа:
а) 1101011110,001(2) + 111100001,011(2); б) 1034,16(8) + 205,2(8); в) 33C,2(16)+37D,4(16). 4. Выполнить вычитание а) 110001100,011(2) - 1101100,11(2); б) 1733,3(8) - 355,2(8); в) 26F,4(16)-D3,6(16).
Р а с ч е т з а д а н и я
1. а)1110010011,1011(2) = 1·29 + 1·28 + 1·27 + 0·26 + 0·25 + 1·24 + 0·23 + + 0·22 +1·21 + 1·20 + 1·2-1 + 0·2-2 + 1·2-3 + 1·2-4 = 512 + 256 + 128 + + 0 + 0 + 16 + 0 + 0 + 2 + 1 + 0,5 + 0 + 0,125 +0,0625 = 915,6875(10)
б) 772,24(8) = 7·82 + 7·81 + 2·80 + 2·8-1 + 4·8-2 = 448 + 56 + 2 + 0,25 + + 0,0625= 506,3125(10)
в) 81,А(16) = 8·161 + 1·160 + 10·16-1 = 128 + 1 + 0,625 = 129,625(10)
2. 119(10)
_ 119 2 118 _59 2
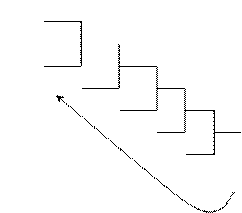 1
58 _29 2 1 28
_14 2 1 14 _7 2
1
58 _29 2 1 28
_14 2 1 14 _7 2
0 6 _3 2
1 2 1
1
Проверка:1110111(2)=1·20+1·21+1·22+0·23+1·24+1·25+1·26=1+2+4+16+32+64=119(10)
_ 119 8
112 _14 8
7 8 1
 6
6
Проверка:167(8) = 7·80+6·81+1·82 = 7+48+64 = 119
|
119 112 |
16 |
|
7 |
_
![]() 7
7
Проверка:77(16) = 7·160+7·161 = 7+112 =119
119(10) = 1110111(2) = 167(8) = 77(16)
3. а) 1101011110,001(2) + 111100001,011(2) = 10100111111,1(2)
+1101011110,001
![]()
б) 1034,16(8) + 205,2(8) = 1241,36(8)
.
+1034,16
![]()
в) 33С,2(16) + 37D,4(16) = 6В9,6(16)
.
+33С,2 37D,4 6В9,6
4. а) 110001100,011(2) – 1101100,11(2) = 100011111,101(2)
. . . . . . . .
– 110001100,011
![]()
б) 1733,3(8) – 355,2(8) = 1356,1(8)
– 1733,3
![]()
в) 26F,4(16) – D3,6(16) = 19В,Е(16)
– ![]() 2 6 F,4 D
3,6
2 6 F,4 D
3,6
1 9 В,Е
Р е з у л ь т а т в ы п о л н е н и я з а д а н и я
1) 1110010011,1011(2) = 915,6875(10)
772,24(8) =506,3125(10) 81,А(16) =129,625(10)
2) 119(10) = 1110111(2) = 167(8) = 77(16)
3) 1101011110,001(2) + 111100001,011(2) = 10100111111,1(2)
1034,16(8) + 205,2(8) = 1241,36(8) 33С,2(16) + 37D,4(16) = 6В9,6(16)
4) 110001100,011(2) – 1101100,11(2) = 100100000,101(2)
1733,3(8) – 355,2(8) = 1356,1(8) 26F,4(16) – D3,6(16) = 19В,Е(16)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.