Совершенствование профессиональной компетентности педагога по предмету «Математика» в условиях реализации ГОС

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ РЕСПУБЛИКАНСКИЙ ИНСТИТУТ

ДОПОЛНИТЕЛЬНОГО ПЕДАГОГИЧЕСКОГО ОБРАЗОВАНИЯ»

ФАКУЛЬТЕТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

И ПРОФЕССИОНАЛЬНОЙ ПЕРЕПОДГОТОВКИ

КАФЕДРА ЕСТЕСТВЕННО-МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН

И МЕТОДИКИ ИХ ПРЕПОДАВАНИЯ

 

 

 

 

ВЫПУСКНАЯ РАБОТА

 

«Особенности преподавания алгебры в 7-9 классах»

 

 

Выполнила слушатель группы 4.6.12

«Совершенствование профессиональной компетентности педагога по предмету «Математика» в условиях реализации ГОС»

 

Крыжановская Яна Викторовна,

учитель математики МБОУ «Школа № 78 г. Донецка»

 

 

Руководитель выпускной работы:

Сипачева Елена Владимировна, старший преподаватель кафедры естественно-математических дисциплин и методики их преподавания

Работа допущена/не допущена_________

(подпись)

 

 

 

 

 

 

Донецк, 2022 г.

 

АННОТАЦИЯ

 

Для современного этапа развития системы школьного образования характерно развитие новых способов образования, педагогических технологий, имеющих дело с индивидуальным развитием личности. Акцент переносится на воспитание подлинно свободной личности, формирование у детей способности самостоятельно мыслить, добывать и применять знания, тщательно обдумывать принимаемые решения и четко планировать действия.

Цель: разработать методические рекомендации по организации качественной работы учащихся 7-9 классов в процессе обучения алгебре.

• Задачи: Выявить психолого-педагогические аспекты организации работы учащихся 7-9 классов.
• Раскрыть особенности обучения учащихся учебному предмету «Алгебра» в 7 – 9 классах.

         В первой главе проведен обзор литературы по психолого-педагогическим закономерностям обучения математике, а также обзор и анализ математического образования в 19-20 вв. Во второй главе рассмотрены методические особенности обучения школьному предмету «Алгебра» в среднем звене школы. Приведены примеры использования отдельных методов обучения и форм контроля качества знаний.

 

 

 

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ

 

Введение

Глава I. Психолого-педагогические закономерности обучения математике

1.1. Психологические особенности формирования мышления в подростковом возрасте

1.2. Обзор и анализ математического образования 19 - начала 20 в.в.

1.3. Обзор и анализ математического образования в 20 в.

Глава II. Методические особенности обучения школьному предмету «Алгебра» в среднем звене школы

2.1. Методы исследования уровня качества знаний по алгебре в 7-9 классах

2.2. Пути реализации методов обучения в преподавании алгебры в 7-9 классах

Выводы

Библиография

 

 

 

 

 

 

 

 

 

 

Введение

         Невозможно переоценить роль математики как предмета в воспитании гражданина нашей Родины, ведь математика учит думать, логически мыслить, на это нацелены стандарты второго и третьего поколения. Именно с математики началось такое осмысление мира, которое лежит в основе становления и развития научного знания. Современная математика по-прежнему является важнейшим инструментом для естественных наук.

         В конце второго тысячелетия область применения математических знаний значительно расширилась. Математика играет важную роль в развитии многих нематематических наук, таких как биология, медицина, социология, психология, статистика, управление производством и т.д. Научно-техническая революция предъявила новые требования к уровню знаний, умений и навыков, к технической культуре, к сфере услуг, к общему и профессиональному образованию. Всё это требует недюжинной математической подготовки во всех отраслях деятельности человека, поэтому перед современной школой ставятся задачи не только совершенствования образования, но и высокой качественной подготовки учащихся к дальнейшей образовательной деятельности.

         Решение вышеупомянутых задач требует повышения уровня как теоретической, так и практической подготовки обучающихся, а, значит, и отбора содержания учебных дисциплин. Реализация задач с точки зрения школьного предмета «математика» требует качественной базисной подготовки всех учащихся, их умение применять теорию в различных отраслях науки.  Полноценному базисному образованию способствует хорошо организованная учебная деятельность, с привлечением всех обучающихся в учебно-воспитательный процесс, через системно-деятельностный подход в обучении по всем предметам и, в частности, алгебре.

         Учебный предмет «Алгебра» оказывает большое влияние на интеллект человека и, прежде всего, таких его компонентов как способность к усвоению нового материала, сила и гибкость ума, критичности, умения планировать действия, способность к аргументации и т.д. Для нахождения путей повышения качества и контроля уровня знаний по данному предмету у каждого учащегося учителю следует исходить из методических особенностей обучения алгебре. Ведь при изучении предметного материала, который носит абстрактный характер, практически отсутствует возможность прикрепить демонстрационно - наглядный материал, при решении задач используют математическое моделирование, в процессе обучения активно используются анализ и синтез, индукция и дедукция, сравнение и аналогия, абстрагирование, обобщение, конкретизация, владение которыми способствует ученику не только понять алгоритмы решения, но и самому их составлять, используя средства программирования.

         Не следует забывать так же, что курс алгебры основной школы имеет большую практическую направленность, которая требует от обучающихся прочного овладения основными понятиями, алгоритмами решений различного рода уравнений и неравенств, умения выполнять различного рода преобразования всевозможных выражений, исследовать функции и строить графики и т.д. Ученики должны иметь твёрдые знания по каждой теме, так как эта информация  является звеном огромной цепи понятий и имеет большое значение в реализации межпредметных связей. Непонимание какого-либо понятия может привести к ошибке и пробелам в обязательных результатах базовой подготовки. Для этого, планируя урок, учитель должен пересмотреть его структуру и учитывать особенности изучаемого материала и объективной системы познания. При этом наблюдается увеличение времени на повторение и закрепление тем. Таким образом, при анализе и переосмыслении, последующем пересмотре роли и места основных содержательных методических линий, из которых состоит курс учебного предмета «Алгебра», нужно приложить значительные усилия для максимального развития способностей обучающихся, чему и помогает личностно-ориентированный образовательный процесс, учитывающий и развивающий индивидуальные способности учеников.

         Мониторинг реформ в системе школьного образования, а также программ и учебников по алгебре за 19 и 20 века позволили выделить ряд причин, которые влияют на качество математического образования.

1.     Направление реформы школьного образования, имеется в виду гуманитарное или техническое;

2.     Выбор учебного пособия;

3.     Профессиональная подготовка учителя-предметника;

4.     Основные методы и формы в работе учителя используемые в процессе обучения школьников;

5.     Способы проверки качества усвоения знаний, приобретенных умений, выработанных навыков.

         Таким образом, проблема исследования состоит в выявлении особенностей содержательных линий учебного предмета «Алгебра» и методических условий их реализации при системно-деятельностном подходе.

Объект исследования: система обучения алгебре в среднем звене школы.

Предмет исследования: содержательные и методические особенности базовой подготовки обучающихся по алгебре в основной школе.

В ходе исследования была выдвинута следующая гипотеза: если в основу процесса обучения алгебре положить системно-деятельностный и личностно-ориентированный подходы к обучающимся, и на основе этого рассматривать принципы и методы обучения и формы контроля качества знаний, то это позволит учащимся на совершенно другом уровне осваивать базисное содержание курса алгебры и осуществлять перенос этих знаний, уменийи навыков в другие научные области.

Были использованы следующие методы исследования:

1.     Изучение и анализ отечественной и зарубежной литературы по педагогике, психологии и методике преподавания.

2.     Анализ содержания программ и учебников алгебры отечественной школы 19 и 20 в.в.

3.     Изучение и анализ диссертационных исследований по данной проблеме.

4.     Изучение и обобщение опыта работы школы.

5.     Личный опыт преподавания алгебры в основной школе.

6.     Организация и проведение констатирующего, поискового и обучающего эксперимента.

Глава I. Психолого-педагогические закономерности обучения математике

1.1. Психологические особенности формирования мышления в подростковом возрасте

         Поставленные перед школой задачи в подготовке учащихся к трудовой деятельности и жизни в условиях современного общества требуют формирование такой личности, которая будет готова принимать активное участие в научно-техническом и социальном прогрессе. Основным видом деятельности для обучающихся является учение, а значит, необходимо изыскивать возможности повышения их активности именно в этом процессе, что будет способствовать не только улучшению качества общеобразовательной подготовки учащихся, но и формированию активной личности.

         В подготовке обучающихся в соответствии с современными требованиями существенная роль отводится математике. Трудности изучения математики тесно связаны со спецификой учебного предмета и обуславливают необходимость учета психологических особенностей мышления, индивидуальных закономерностей познавательной деятельности учащихся.

         Не секрет, что обучение в российской школе выполняет три главные функции: воспитательную, образовательную и развивающую. Поставленные задачи предполагают развитие у обучающихся самостоятельного мышления, активизацию их познавательной деятельности, творческой инициативы. Исследованиями психологов (Богоявленского Д.Н. [13], Выготского Л.С. [20], Крутецкого В.А. [35], Леонтьева А.Н. [41], Менчинской Н.А. [13], и т.п.) определено, что по-настоящему усваивается учащимися лишь то содержание, которое является предметом их активных действий, причем эти действия должны полностью соответствовать содержанию изучаемого материала.

         Поставленные задачи можно реализовать в жизнь путем систематического обучения школьников эффективным рациональным приемам умственной деятельности и учебной работы. Необходимость учета психологических особенностей мышления и формирования приемов умственной деятельности учеников в процессе обучения математике обсуждают в последние годы не только психологи, дидакты, методисты, математики, но и учителя-практики. Поэтому учителю следует знать, через реализацию каких мер можно сформировать у обучающихся приемы общих и специфических умственных действий, входящих в состав различных видов учебно-познавательной деятельности.

         В последнее десятилетие в психологической и педагогической науке, в школьной практике активно внедряются пути и средства активизации познавательной деятельности учащихся. При этом познавательная деятельность рассматривается и как средство овладения знаниями, умениями и навыками, и как значимый источник умственного развития учеников.

         При подготовке к уроку учитель внимательно выбирает учебный материал, выделяет в нем "единицу усвоения", продумывает формы и пути его представления, вычленяет, программирует способы деятельности учащихся, то есть те умственные действия и приемы учебной работы, с помощью которых школьники будут усваивать запланированный учебный материал. Следует также учитывать уровень знаний, действий и приемов, которыми учащиеся уже владеют, не забывать об особенностях восприятия, памяти, мышления, возрастных, индивидуальных характеристиках учащихся на разных этапах обучения. Выбор способов усвоения программного материала по предмету зависит от конкретных целей, особенностей его содержания, уровня подготовленности учащихся к восприятию новой темы и т.п. Поэтому на одних уроках учебный материал может объясняется учителем, а воспроизводится и закрепляется обучающимися, а на других уроках -  организуется поисковая деятельность. Важно выбрать такой способ организации познавательной деятельности учащихся, при котором они в процессе усвоения материала овладевают рациональными приемами практических и умственных действий. Общие и специфические приемы умственных действий должны стать объектом усвоения и сознательного их применения, контроля со стороны учителя и самоконтроля учащихся. Считается полезным обучать учеников правилам выполнения отдельных видов умственных действий, правилам-ориентирам, эвристическим схемам основных видов учебной деятельности.

         По мнению психологов, наиболее общим показателем умственного развития школьника является его обучаемость. Калмыкова З.И. выделяет следующие компоненты обучаемости:

-"обобщенность мыслительной деятельности, направленность на абстрагирование и обобщение существенного в материале,

-осознанность мышления, определяемая соотношением его практической и словесно-логической стороны,

-гибкость мыслительной деятельности,

-устойчивость мыслительной деятельности,

-самостоятельность мышления, его восприимчивость к помощи

         Упоминая развитие умственных способностей и мышления при помощи математики, следует подчеркнуть сущность математической науки. По мнению Колмогорова А.Н. "сущность математики составляют абстракции и обобщения, а особенностью её является специальный язык, знаковая символика. Овладевание математическими знаниями развивает способности обобщать, абстрагировать, формализовать знания, оперировать формальными структурами, числовой и знаковой символикой, переводить на язык символов словесно сформулированное закономерности, находить пути решения, не подходящие под стандартнее правила. [32, с.9] Хинчин А.Я. отмечал влияние математических знаний на формирование, мировоззрения, интеллектуальных и моральных качеств личности учащегося. [16, с. 146-157]

Таким образом для активизации мыслительной деятельности на уроках математики и не только на них, учителю следует знать:

1) особенности развития учащихся на данном этапе учебы;

2) формы и методы исследования знаний учащихся;

3) пути совершенствования умственной деятельности.

1.2. Обзор и анализ математического образования 19 - начала 20 в.в. 

         Известно, что система образования России была трехступенчатой и предполагала преемственность учебных заведений. Гимназии считались учебными заведениями средней ступени. Учреждение гимназий имело двойную цель: во-первых, это была подготовка к высшей ступени российского образования - университету, во-вторых, это была возможность приобрести знания и «сведения, необходимые для благовоспитанного человека».

         Содержание математического образования в гимназиях в конце 19 века – начале 20 века претерпело существенные изменения, в связи с событиями, которые происходили в жизни российского общества. Этот исторически период характеризуется плодотворной законодательной деятельностью в области российского просвещения. Так, 19 ноября 1864 года Александром II утвердил "Устав гимназии и прогимназии", по которому: "вводились в России гимназии двух типов (с семилетним курсом обучения):

1) классическая гимназия, в двух вариантах: с двумя древними языками и с одним древним языком;

2) реальная гимназия без древних языков, но со значительным увеличением числа часов на иностранные языки, естествознание, чистописание, черчение и некоторым прибавлением часов на русский язык, математику и космографию.

         Для поступления в гимназию требовалось знание всего курса приходского и уездного училищ. Значит, учащимся, которые претендовали на звание гимназиста, нужно было владеть большим объемом учебного материала, что и указывалось в прошении о зачислении в гимназию.

         Учебные программы гимназий, как общегосударственные, явились развитием учебных государственных программ, впервые утвержденных в русских гимназиях вместе с уставом 1871 г. До того периода общеобязательных программ не существовало.

         В отличие от мужских, учебные программы женских гимназий в разделе «математическое образование» были гораздо проще. Например, в женских гимназиях логику изучали на год позже, чем в мужских, не преподавали тригонометрию, и, вообще, на изучение курсов алгебры и геометрии было выделено меньшее количество часов. Потому что у мужчин была возможность продолжить образование в университете, а женщины не могли это сделать, для них высшей ступенью обучения была гимназия.

          30 июля 1871 года Александром II утвердил, предложенный министром "Устав гимназии и прогимназии Министерства народного просвещения", по которому за гимназиями сохранялась и закреплялась привилегированность средних учебных заведений. Устав признавал только классические гимназии с двумя древними языками и прогимназии; реальные гимназии стали реальными училищами. Целью гимназии признано общее образование и подготовка к обучению в университете. Гимназии состояли из 7 классов, но седьмой — с двумя годичными отделениями (с 1875 года гимназии стали  восьмиклассными). Прогимназии могли быть и шестиклассные. При каждой гимназии был приготовительный класс. Особенности нового учебного плана: признание главного значения за древними языками (число уроков по латинскому языку доведено до 49, а по греческому — до 36), прекращение преподавания естественной истории (сначала в низших классах, а потом и вовсе), замена космографии математической географией, введение логики, уменьшение числа уроков чистописания, рисования и черчения, уменьшение числа уроков по истории (с 14 на 12) и по закону Божию (с 14 на 12), введение географии в VII и VIII классах (повторение).

         Как уже упоминалось, ведущими предметами учебного курса гимназий признавались древние языки и математика. Им отводилась большая часть учебного времени (диаграмма 1).

Диаграмма 1.

Количество часов для изучения основных предметов в гимназиях.

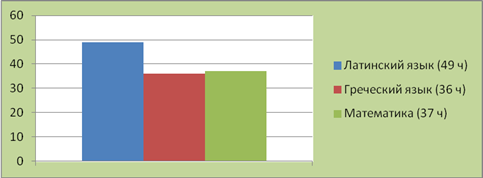
         Таким образом, на изучение латинского и греческого языков отводилось 85 годовых часов* (41,5% всего учебного времени), на изучение математики (вместе с курсами физики, естествознания и математической географии) приходилось 37 часов (18% учебного времени). Изучение математики носило академический, традиционный характер. Содержание гимназического образования было следующим:

- с I по III классы изучалась алгебра, геометрия и плоская тригонометрия (6 часов в неделю);

- с IV по VII классы изучалась прикладная математика, в состав которой входили: механика, гидравлика и опытная физика (6 часов в неделю).

         В современном кабинете математики можно найти большое количество различных инструментов, приспособлений, наглядных пособий, технических средств. Что же использовали гимназисты конца 19 – начала 20 веков при изучении математики? Это, прежде всего, живое слово учителя, как "главнейшее средство обучения". Наглядные пособия делились на:

- чисто-наглядные (числовые фигуры, чертежи, доска);

- наглядно-осязательные (пальцы рук, предметы для счета, палочки);

- наглядно-вычислительные (русские счеты, шведские счеты, спички, пальцы рук, таблица умножения и т. д.);

- наглядно-измерительные (модели единиц меры);

- геометрические (геометрические чертежи и тела).

         В конце 19 века – начале 20 века математике принадлежала роль одного из опорных предметов гимназического образования. Сложившиеся тогда представления об объеме и содержании общих школьных курсов математики были зафиксированы на многие десятилетия в легендарных учебниках. Таким образом, в рамках реформы 1871 г. окончательно оформилась традиция массового математического образования достаточно высокого уровня, охватившая все среднее образование и пережившая революционные события начала 20 века.

1.3. Обзор и анализ математического образования в 20 в.

         История отечественного школьного математического образования с середины 19 в. до наших дней прошла через 5 основных этапов:

1. Этап начала объёмных научных изысканий в области проблемных вопросов математического образования (1860-1910 гг.).

2. Этап всероссийских съездов учителей математики (1911-1917 гг.).

3. Этап становления послереволюционной школы и поиска новых путей постановки школьного математического образования (1918— 1932 гг.).

4. Этап возрождения отечественных традиций и попыток совершенствования общеобразовательной трудовой политехнической школы (1931-1964 гг.).

5. Современный период (1965 и последующие годы).

         Возникший в России 19 веке широкий интерес к разработке теории обучения и воспитания распространялся и на вопросы математического образования. Уже с первой половины 19 в. вопросы преподавания математики стали активно обсуждаться внаучных математических кругах. Но это обсуждение велось сначала в общепедагогических изданиях и имело, главным образом, эпизодический характер. Но увеличение количество учителей и поклонников математической науки вызвало потребность регулярного обсуждения возникающих проблем, что и вылилось во второй половине столетия в появление специализированных журналов.

         Организованный в 1905 г. Московский математический кружок начал с 1912 г. выпускать свой журнал «Математическое образование», редактором которого был профессор Московского университета и Высших московских женских курсов И.И. Чистяков. Журнал выходил в 1912-1917 гг. (48 номеров) и в 1928-1930 гг. (24 номера). Новизна, сложность и актуальность рассматриваемых в публикациях методических вопросов показала, что необходимо более существенное их обсуждение, чем это было возможным на страницах изданий.

         В промежутке 1911-1912 гг. был проведен 1-ый Всероссийский съезд уителей математики, собравший свыше 1200 участников. Наибольшее число сообщений на съезде отводилось вопросам общей и специальной методики.       Второй съезд учителей математики был посвящён таким вопросам: обсуждение пунктов, имеющих отношение к элементарной математике; рассмотрение современной постановки преподавания математики в учебных заведениях, в основном — в средних; обсуждение вопросов о желательной постановке преподавания математических наук; обсуждение вопросов о методах и приемах преподавания математики и соприкасающихся с нею наук и о способах проверки знаний учащихся; обсуждение вопроса о подготовке уителей математики. В принятой II съездом резолюции предлагался ряд мер по улучшению подготовки преподавателей математики, обновлению школьного обучения.

         После проведения съездов произошли небольшие изменения в программе. Новые программы оказались лучше в сравнении с программами 1890 и 1906 гг., но общий характер не претерпел изменений.

         До начала 30-х гг. 20 в. в школьном математическом образовании мирно уживались два взаимонезависимых направления. Первое направление отражало стремление к продолжению реформ, намеченных I и II всероссийскими съездами уителей математики, а второе направление действовало под руководством из центра и создавало «новую школу».

         Не удивительно, что второе направление возобладало. Но и сторонники первого направления продолжали свое творческое дело.

         Начало должному вниманию к прошлому опыту положили правительственные постановления 1931—1932 гг. «О начальной и средней школе». В школах возобновлялось регулярное изучение курса математики. Возвращались классно-урочная система занятий и предметное преподавание. Появились единые для всего государства типы общеобразовательных школ и ступени образования: начальная (1-4 классы), неполная средняя (5-7 классы) и средняя (8-9 классы). Вводились стабильные учебники. Математику стали преподавать по учебникам, действовавшим в дореволюционной школе (после их незначительной правки).

         Большой вклад в восстановление положительных традиций был сделан Министерством просвещения РФСФР, которое на тот момент возглавлял А.С. Бубнов. Под его руководством прошло Всероссийское совещание (1935 г.), на котором обсуждался ряд проблем, были намечены вопросы для рассмотрения на III Всероссийском съезде уителей математики. Принятые решения данного совещания оказали существенное влияние на восстановление в школе благоприятных условий для учебной работы.

         В послевоенные годы, в связи с созданием Академии педагогических наук, расширилось и участие крупных ученых-математиков в изучении и разработке методических вопросов.

         С 1947 г. возобновилась работа по созданию проектов новых школьных программ по математике. В первом проекте, разработанном в Институте методов обучения АПН с участием И.В. Арнольда, B.JI. Гончарова, Я.С. Дубнова, Н.Ф. Четверухина, А.И. Маркушевича, особенности программы разъяснялись таким образом: «При составлении проекта программы по математике особое значение придавалось приближению программ к современному состоянию математической науки. Сюда, в первую очередь, относятся понятия переменной величины, функциональной зависимости и преобразования (в геометрии) и ознакомление с простейшими классическими методами их изучения (элементы анализа и аналитической геометрии)».

         В июне 1964 г. под руководством Министерства просвещения РСФСР прошло совещани, посвящённое проблемам математического образования в средней школе.         В 19 - 20 вв. сохраняется преемственность в содержании математики как единого учебного процесса с табличной формой изложения правил, практикой преподавания, богатой математической терминологией на арабском языке, системой народных мер и весов. Усиливается связь учебного материала по математике с другими предметами: географией (календарь, съемка плана, измерение на местности с выходом в поле), черчением (обучение построению чертежей геометрических тел и фигур) и др. Происходит разделение элементарной математики на учебные предметы (алгебру, геометрию с тригонометрией), которые излагаются в школах общеобразовательного типа как самостоятельные дисциплины. Появляются и начинают функционировать новые виды учебных заведений. Создаются учебники и задачники, в составление которых включаются народные просветители и передовые учителя-практики. В конце 19 в. зарождаются новаторские идеи необходимости сближения учебного предмета математики с математической наукой, связи изучения математики с жизнью.

Глава II. Методические особенности обучения школьному предмету «Алгебра» в среднем звене школы

2.1. Методы исследования уровня качества знаний по алгебре в 7-9 классах

         Процесс обучения не может быть эффективным без взаимодействия "учитель-ученик", ведь именно эта взаимосвязь даёт учителю информацию об уровне знаний, умений и навыков, о возникающих трудностях, не только всего класса в целом, но и для каждого ученика в отдельности. Обратную связь учитель может осуществить с помощью диагностического контроля, а также использовать обратную связь для выяснения достижения целей обучения на каком-либо конкретном этапе и как более быстро и эффективно устранить пробелы в знаниях.

         В современных реалиях, совершенствование системы образования, целесообразно организовывать, реализуя системно-деятельностный подход. При этом учёт знаний, умений и навыков, при котором каждый учащийся оценивается по всем основным разделам любой темы курса математики, становится главным средством реализации данного направления.

         При этом возникают вопросы: "Как хорошо подготовить и провести урок, как верно оценить проведенный урок, ведь это всецело влияет не только на развитие знаний, умений и навыков, но и на особенности мышления учащихся?", "Как можно организовывать именно такой диагностический контроль, который дал бы учителю возможность управлять процессом обучения, повышать качество усвоения учебного материала и определять фактическое соответствие уровня знаний обучающихся требованиям программы?"

         Всем этим критериям соответствует контроль с личностно ориентированным тематическим учетом знаний, направленный на личностные особенности каждого ученика, при котором проверяются и фиксируются по каждой теме знания, умения, навыки.

         Для этого целесообразно вести индивидуально-тематический учет знаний при помощи табличных форм, где будут указаны: тема, список учащихся с их индивидуальными особенностями, знания, которые необходимы для овладения данного материала, и умения, которые будут подтверждать теоретическую осведомленность.

         Анализируя такой учёт, можно увидеть, в работе с какими понятиями учеником допущено наибольшее количество ошибок и, каким способом эти ошибки можно проработать. В случае, когда учителю нужно посмотреть, усвоение предметного материала на уровне всего класса, то можно построить диаграмму или диагностическую кривую, испоьзуя результаты таблицы.

         Для более подробной оценки знаний и умений сам учитель может разработать свою методику расчета коэффициента усвоения тематического материала. Для этой цели учителю нужно составить задания из 15-20 вопросов, охватывающих основные пункты темы, которые имеют применение в дальнейшем процессе обучения: знание определений, теорем, формул, свойства и т.д.

         Правильный ответ равен одному баллу, неправильный ответ равен нулю, тогда отношение суммы правильных ответов к количеству вопросов и будет коэффициентом усвоения предметного материала. Учитель, конечно же, может сам установить шкалу оценок. Такая диагностика легко применима при использовании любой формы контроля. Она будет являться хорошим дополнением к контролю с личностно-ориентированным учетом знаний.

         Планируя изучение темы, учитель определяет способы проверки знаний, умений и навыков. Некоторые умения целесообразно проверить с помощью письменной работы, другие - с помощью математических диктантов, тестов или путем комбинированного опроса у доски. Но независимо от формы проверки усвоения предметного материала учитель должен вести личностно-ориентированный тематический учет с помощью табличных форм. Такие таблицы по темам можно заранее приготовить на всю учебную четверть в 7-9 классах, или на весь семестр в 10-11 классах и заполнять их по мере прохождения тематического материала.

         Во время проведения итоговых контрольных работ даются комбинированные задачи, задания из разных тем, а, следовательно, в связи с этим трудно проследить усвоение какой-то отдельно взятой темы, поэтому в этой ситуации личностно-ориентированный тематический учет неуместен. Но в ходе проверки итоговых работ на первый план выходят такие личностные качества, как внимание, способность к анализу и синтезу, присутствие логического мышления и естественно знание основ теоретического и практического материала. С обучающимися, имеющими пробелы в знаниях, проводится индивидуально-групповая, консультативная работа с проверкой результатов при помощи математических диктантов или тестов.

         Вопрос выбора метода проверки или сочетание методов проверки всегда будет стоять остро на повестке дня. Методы проверки знаний, умений и навыков разительно отличаются между собой по критериям сущности, мотивации, возможности отражать разные уровни усвоения знаний и характер учебно-познавательной нагрузки обучающихся. Выявление знаний, как известно, осуществляется методами письменной и устной проверки. По организации проведения проверка может быть индивидуальной и фронтальной. Сочетание методов и организационных форм определяет вариативность проверки знаний, умений и навыков учащихся, в зависимости от ситуации и личностных особенностей используются различия в ее целях и направленности.

         Устная проверка, достоинство которой заключается в непосредственном контакте между учителем и учеником, знания которого проверяются в данный момент, - один из самых распространенных методов проверки знаний. В ходе применения данного метода учитель непосредственно следит за ходом мысли тех, кто отвечает и при необходимости корректирует ответ.

         Учитель, основываясь на личностных качествах ученика, может и должен проявлять определенную гибкость в зависимости от той или иной ситуации. Например, если ученик, со слабой подготовкой по предмету получил задание решить неполное квадратное уравнение и при его решении он использует общую формулу корней квадратного уравнения и приходит к правильному ответу, то его надо похвалить и при этом подчеркнуть универсальность примененной формулы; если же такой ответ дает потенциальный отличник, то надо заметить, что этот способ не рационален, а значит, ведет к существенной затрате времени. Но не только учитель следит за логикой ответа ученика; важно подключить к этой деятельности весь класс. Ведь вопрос можно поставить фронтально перед всем классным коллективом, и лишь только после определённой паузы выслушать ответ ученика, после которого классу можно задать такие вопросы: "Кто не согласен с ответоми почему?", "Какие неточности были допущены при ответе?". Такая проверка даёт прекрасную возможность выработать умение пользоваться словами для выражения своих мыслей, отшлифовать грамотность речи обучающегося, умение четко и корректно излагать суть вопроса. Если ученик испытывает трудности при ответе, то учителю, исходя из рассуждений ученика, следут помочь обучающемуся выстроить аргументированный ответ. Самое главное, чтобы учитель не концентрировал всё внимание на одном отвечающем, а смог привлечь весь класс к обсуждаемой проблеме.

         Такая работа хорошо проводится при постановке проблемной ситуации. Например, когда надо решить квадратное неравенство, а соответствующий график функции не имеет точек пересечения с осью абсцисс.

         Устная фронтальная проверка помогает установить знания по данному тематическому материалу и умение применять его на практике большинством учащихся класса. Для этого лучше разбить проверочный материал на отдельные части, к которым можно задать вопросы, логически связанные между собой и подводящие учеников к определенным выводам.

            Актуальность устной проверки заключается в следующем:
1. Устные упражнения способствуют повышению общего уровня математического образования и сознательному усвоению школьного курса.
2. Устные упражнения развивают у учеников навык быстро выделять из известных им законов, формул, теорем те, которые следует применить для решения предложенных или возникших в практике задач, расчетов и вычислений.
3. Устные упражнения содействуют развитию памяти, развивают способность зрительного восприятия математических фактов, совершенствуют пространственное воображение.
         Устные упражнения имеют огромное значение и с чисто воспитательной точки зрения: они повышают внимательность, развивают сообразительность, находчивость, творческую инициативу. Особое значение имеет и то, что устные упражнения повышают темп работы, требуют отыскания наиболее рациональных приемов решения предложенных задач, содействуют развитию устной речи, лаконичной и четкой. Устные упражнения становятся действенными только в том случае, если они проводятся систематически, а не от случая к случаю. Подобная проверка хорошо зарекомендовала себя в начале урока, когда проводится повторение материала предыдущих уроков или давно пройденный материал, знание которого важно для качественного усвоения новой темы.

2.2. Пути реализации методов обучения в преподавании алгебры в 7-9 классах 

         Введение новых школьных программ вызвано изменением в системе образования, курс которой взят на переход на российские стандарты. Предметам математического цикла стало отводиться меньше учебного времени, но объем программы остался почти прежним. Учителя математики вынуждены использовать все свои знания, умения и приемы, перестроить свою работу так, чтобы ученикам доступнее объяснить изучаемый материал, не отбив при этом желание учиться, получать новые знания и совершенствовать уже имеющиеся.

         Методам обучения, от которых зависит немалый успех работы учителя и школы в целом, посвящен не один десяток фундаментальных исследований. И, несмотря на это проблема методов обучения, как в теории обучения, так и в педагогической практике остается весьма актуальной. Понятие метода обучения является весьма сложным. Это обуславливается исключительной сложностью того процесса, который призвана отражать эта категория. Многие авторы считают метод обучения способом организации учебно-познавательно деятельности учащихся. Поэтому мы поставили себе задачу, проанализировать основные методы обучения, проиллюстрировать применение отдельно взятой группы методов в курсе обучения алгебре 7-9 классов при системно-деятельностном подходе.

1.    Словесные методы обучения (рассказ, лекция, беседа).

2. Методы, которые определяются уровнем познавательной деятельности обучающихся (проблемно-поисковый, самостоятельной работы).

3.    Логические методы обучения (анализ и синтез, индукция и дедукция, сравнение и аналогия, абстрагирование, обобщение и конкретизация).

4. Эмпирические методы обучения (наблюдение, описание, измерение, эксперимент).

5. Математические методы обучения (математическое моделирование, аксиоматический).

6. Логико-алгоритмические методы обучения (алгоритмизация обучения, программированное обучение).

         Широко распространенными методами обучения, которые применяются при изложении нового материала, являются рассказ и лекция учителя. Используя данные методы, учитель может непосредственно опираться на личностные качества ученика и формировать их в процессе обучения, т. е. организовать учебный процесс с точки зрения не только системно-деятельностного, но и личностно-ориентированного подхода. При этом появляется иллюзия, что активная роль во время использования этих методов принадлежит только лишь учителю, а учащиеся должны внимательно слушать и аккуратно выполнять те записи, которые учитель делает на классной доске, таким образом следуя своей пассивной роли ведомого. Но это только при беглом взгляде на данные методы, ведь при таком подходе эти методы обучения были бы малоэффективными, а мы установили в 1-ой главе нашего исследования, что важное условие продуктивной работы ученика – это его активная познавательная деятельность. Поэтому учебные рассказ или лекция призваны пробудить у учащихся естественный интерес и активную умственную деятельность. Слушая объяснения учителя в форме рассказа или лекции, предполагается, что вместе с учителем учащиеся должны следовать путём поиска, исследования, установления и обоснования изучаемых математических фактов и их возможных вариантов.

         Рассказ как метод обучения математике находит, к сожалению, крайне небольшое применение, а для изложения предметного материала он почти не применим. Но учитель может прибегать к этому методу для сообщения исторических справок о развитии математической науки, сведений о жизни и деятельности великих ученых-математиков, что значительным образом способствует развитию общей культуры учеников и формированию их познавательного интереса. Увлекательный рассказ можно сделать введением или заключением к изложению отдельных глав или тем, например, посвященных решению уравнений или неравенств. Поэтому при использовании рассказа, как словесного метода обучения учителю следует помнить, что данный метод:

-предполагает использование таких методических и логических приемов как: активизация внимания, сравнение, сопоставление, выделение главного, резюмирование,

-характеризуется недостаточной долей самостоятельного познания, поисковой деятельности учащихся,

-затрудняет обратную связь между учителем и учениками о качестве усвоенной информации,

-не может учесть индивидуальных способностей всех учащихся.

         В результате этого условиями эффективного применения рассказа выступают: чёткое планирование урока с учётом индивидуальных способностей учащихся, выбор наиболее корректной последовательности раскрытия темы, удачный подбор примеров и наглядных пособий, поддержание соответствующего эмоционального настроя и атмосферы изложения.

         Например, знакомя учеников 7 класса с понятием функции, можно рассказать об историческом развитии этого определения, о великих ученых В.Лейбнице и Б.Больцано, которые ввели многие понятия и символы, употребляемые в математике и сейчас.

         Если учителю предстоит рассмотреть вопрос о классификации уравнений и их решениях, об исследовании функций, построении их графиков или повторить обзорно прошедший материал, то наиболее подходящим методом обучения может послужить лекция, так как изложение материала сопровождается объёмными и сложными математическими выкладками, которые базируются на большом количестве изученного ранее материала.

         Лекционное изложение целесообразноиспользовать, если программный материал достаточно сложен для его изучения учениками, или важен, с точки зрения его целостного восприятия для учащихся. Поэтому при подготовке лекции учителю нужно обязательно учитывать не только математическую подготовку классного коллектива в целом, но и отдельно взятые личностные качества учащихся. Это изложение можно прервать для повторения учащимися того, что дано и к чему требуется прийти: это способствует лучшему пониманию излагаемой информации; иногда, по ходу содержания материала, можно прервать объяснение и ответить на возникшие у обучающихся вопросы, а затем продолжить изложение. Школьная лекция всегда заканчивается выяснением кому и что непонятно в объяснении, и ответами учителя на все возникшие вопросы.

         При использовании школьной лекции учитель должен обязательно иметь в виду следующие факторы:

-лекция представляет собой определенную логическую систему умозаключений, из которых нельзя потерять или недопонять ни одного звена, так как изложение разорвется, станет непонятным, поэтому учащимся предъявляется требование сконцентрироваться на излагаемом, внимательно слушать, не пропуская ни одного вывода,

-школьники практически не имеют возможность проявить инициативу, находчивость изобретательность,

-учитель-предметник, в определённой мере, лишен возможности оценить, верно и хорошо ли понят учениками излагаемый материал.

         Поэтому в ходе ведения лекции учителю нельзя отступать от четкого плана, нужно акцентировать внимание учащихся на главных вопросах темы, сопровождать объяснение ясной и четкой записью или комментариями на школьной доске, помня о возрастных особенностях учащихся для более эффективной концентрации их внимания.

         Например, для более качественного применения школьной лекции при обзорном повторении всего курса алгебры в 9 классе, лекционно могут быть освещенны следующие темы:

1. Виды уравнений и способы их решений

2. Неравенства и способы их решения

3. Классификация фушщий и их графики

4. Обобщение понятия степени

         Одним из достаточно эффективных методов обучения математике, способствующему активному и творческому усвоению обучающимися нового материала, является беседа. Во время беседы происходит обмен мнениями между учениками и учителем, совместно, через восстановление цепочки логических выводов решаются задачи, делаются правильные умозаключения. При этом учителю удается активизировать коллективную работу класса, научить школьников совместно строить гипотезы, различные предположения и находить пути к их разрешению.

         Чтобы беседа имела обучающий характер и не превратилась в хаос на уроке, учителю при составлении конкретного плана урока-беседы нужно:

-точно сформулировать и записать все основные и дополнительные вопросы,

-вопросы расположить последовательно по мере возрастания их сложности,

-заранее подготовить те наглядные пособия, которые понадобятся в ходе урока.

         При точно выбранной теме, при хорошем знании особенностей каждого ученика класса беседа открывает широкие возможности установления наиболее выгодного режима работы, подходящегодля каждого участника учебно-воспитательного процесса, а также создает условия для учета интересов и способностей каждого ребёнка. Беседа предполагает не только фронтальную постановку вопроса, но и длительное общение с каждым учеником. В беседе раскрывается самостоятельность мышления, инициативные высказывания, ложность высказываний, допущенная в предположениях, интересы и увлечения школьников, формируется логическое мышление, умение прислушиваться к мнению других, развиваются познавательные интересы, а самое главное, происходит непосредственное общение между всеми участниками педагогического процесса. По мнению Ламберга Р.Г.: "Беседа - одно из верных средств, способствующих сближению между педагогом и его воспитанниками. [40, с.60]

Выводы

 

         Итак, в ходе данной работы, было установлено, что:

1) Личностно-ориентированный и системно-деятельностный подходы -  это главное средство повышения качества усвоения базисной математической подготовки обучающихся среднего звена школы, что даёт возможность учащимся на ином уровне осваивать основное содержание курса учебного предмета «Алгебра» и осуществлять применение полученных знаний и умений в других научных областях;

2). Курс учебного предмета «Алгебра» среднего звена школы должен включать в себя обе ветви современной математики (теоретическую и «прикладную) и отражать их научное единство.

         Также были получены следующие результаты:

l. Основываясь на анализе эволюции содержания школьного математического образования в России в 19—20 в. в., были выявлены тенденции его совершенствования в основной школе в ходе предстоящей реформы системы образования:

• стабилизировано количество недельных часов на математические дисциплины (алгебра, геометрия);

• имеет место плавный переход от изучения одной математической дисциплины к другой;

• прослеживается взаимосвязь изучаемых школьных математических дисциплин друг с другом (арифметика и алгебра, алгебра и геометрия и др.);

• произведено внедрение в школьный курс алгебры основной школы функциональной линии;

• чёткое выделение содержательных линий школьного курса по алгебре в основной школе (числовая, тождественных преобразований, функциональная, уравнений и неравенств, стохастическая);

• распределение программного материала по алгебре в основной школе по циклам (7 класс: линейная функция, линейное уравнение, системы линейных уравнений, степень с натуральным показателем, преобразование выражений в многочлены и др.; 8 класс: преобразование дробнорациональных выражении, линейные неравенства, квадратные корни, квадратные уравнения, степень с целым показателем и др.; 9 класс: квадратичная функция, квадратные неравенства, решения уравнений, сводящихся к квадратным, степень с дробным показателем); 10 класс: показательная и логарифмическая функции, тригонометрия, стохастика.

• сокращён и упрощён учебный материал ныне действующих программ по алгебре основной школы (исключены темы решения уравнений со многими неизвестными, извлечение квадратных корней из чисел, комплексные числа, решение необратимых уравнений, логарифмическая функция и логарифмическая линейка, отказ от теоретико-множественного подхода и др.);

• теоретический и практический материал сочетаются естественным образом, что в значительной мере способствует достижению общего математического развития учеников.

2. Сформулированы основные требования к совершенствованию математического образования, в частности обучения алгебре в основной школе:

• Необходимо детально проанализировать предшествующий опыт развития отечественной школы и спрогнозировать конечный результат реформирования;

• Ежегодно проводить итоговые контрольные срезы по основным знаниям и умениям, предусмотренным программой, с последующей диагностикой результатов;

• Необходимо каждые 5 лет подводить итоги реформаторскойработы, взвешивая все достоинтсва и недостатки, с исправлением допущенных просчетов;

• Основной задачей в образовании и воспитании установить воспитание всесторонне развитой, творческой личности, свободно владеющей основами школьного курса, ориентирующейся в основах экономической и политической жизни страны, являющейся патриотом своей Родины, стремящейся трудиться на благо своей страны;

• Усилить в школьном курсе роль физико-математических дисциплин, как основы общего образования в условиях научно-технического прогресса, развития компьютеризации производства, с внедрением компьютерной техники, диагностирующих приборов во все отрасли науки и искусства.

3. а). На основе анализа психолого-педагогической литературы по проблемам особенностей формирования мышления в подростковом возрасте и повышения уровня знаний при личностно-ориентированном подходе показаны возможности совершенствования умственной деятельности, познавательной активности и выработки навыка учащимися основной школы, через:

• Развитие у школьников самостоятельного мышления,

• Активизацию их познавательной деятельности,

• Формирование логических приёмов мышления (анализ, синтез, индукция и т. д.). б). Анализ научно-методической литературы позволил выделить пути реализации обучения алгебре в основной школе в условиях личностно-ориентированном подхода, в соответствии с которыми исследователи выработали систему эффективной проверки качества и их совершенствование в зависимости от выявленных пробелов. Для этого учителю необходимо вести диагностический контроль, который представляет собой многогранную систему, включающую в себя:

• контроль с личностно-ориентированным тематическим учётом знаний, направленный на личностные особенности каждого ученика, при котором проверяются и фиксируются знания, умения и навыки по каждой теме. Для этого необходимо вести при помощи таблицы, в которой будут указаны тема, список учащихся с их индивидуальными особенностями, знания, необходимые для овладения данной темой и умения, которые будут подтверждать теоретическую осведомлённость;

• разработку методики расчёта коэффициента усвоения учебного материала;

• разнообразные формы проверки качества знаний: устная проверка (индивидуальная и фронтальная), письменная проверка (индивидуальная и фронтальная), практическая проверка.

в). В соответствии с данной методикой сформулированы условия объективности суждений о качестве знаний ученика при личностно-ориентированном подходе:

• использование разнообразных способов проверки знаний;

• тщательное продумывание комплекса упражнений;

• систематическое проведение проверки качества знаний;

• сопоставление полученных результатов с требованиями базисной программы и их анализ с учётом учебных возможностей ученика.

         г). Определены основные условия обучения личности школьника при личностно-ориентированном подходе, необходимые для более качественного усвоения программного материала:

• при объяснении нового материала учитывать общий уровень математической подготовки класса, организовать в начале объяснения повторение ранее пройденного материала, знание которого необходимо для более быстрого и качественного усвоения новой темы,

• в ходе закрепления материала необходимо давать задания в порядке возрастания трудности, т. е. дифференцируя их,

• при повторении и обобщении следует ранжировать материал по степени его сложности, задействуя при этом сильных и слабых учеников,

• при организации проверки вести личностно-тематический учёт, с целью выявления пробелов в знаниях и качественный рост каждого ученика,

• при выведении оценки учитывать не только процент правильно выполненных заданий, но и соответствие проделанной каждым учащимся подготовительной работы исходя из его потенциальных возможностей.

• организуя работу над ошибками, для каждого учащегося составлять своего рода небольшую программу его действий, состоящую из теоретической части и дифференциальных к ней заданий.

         В условиях общеобразовательной школы надо предельно жёстко определить минимальный необходимый уровень технической подготовки. Но при этом добиваться овладения основами математической культуры как важным средством развития мышления и ориентации в мире. Главное – научить мыслить, рассуждать, доказывать. Одна из задач сегодня – продвинуться в понимании того, как успешно решать профессиональные задачи учителям математики, адекватно отвечая на вызовы времени, на современные потребности государства и общества. Как обнаружить и пробудить талант, дать ему раскрыться в полную меру, как готовить умных и знающих, творческих и целеустремлённых, любознательных и трудолюбивых. Это нелегко, но настоящий учитель математики не боится трудностей, не ищет лёгких путей. Он ищет пути правильные – ведущие к поставленной цели.

 

Список использованной литературы

1. Александров П.С., Колмогоров А. Н. Алгебра. -М.: Учпедгиз, 1939. -192с.

2. Алимов Ш.А., Ильин В. А., Колягин Ю. М. и др. Алгебра: пробные учебники для 6-8 классов средней школы. Под ред. Тихонова А. Н.—М: Просвещение, 1981. -544с.

3. Алимов Ш.А., Колягин Ю. М., Сидоров Ю. В. и др. Алгебра 7 под ред. Тихонова А.Н.—М: Просвещение, 1995. -190с.

4. Алимов Ш.А., Колягин Ю. М., Сидоров Ю. В. и др. Алгебра 8 под ред. Тихонова А.Н.—М: Просвещение, 1996. -238с.

5. Алимов Ш.А., Колягин Ю. М., Сидоров Ю. В. и др. Алгебра 9 под ред. Тихонова А.Н.—М: Просвещение, 1998. -220с.

6. Андронов И.К. Полвека развития школьного математического образования в СССР. —М: Просвещение,1967. -180с.

7. Бабанский Ю.К. Методы обучения в современной общеобразовательной школе. —М: Просвещение, 1985. -208с.

8. Барсуков А.Н. Алгебра. —М: Учпедгиз, 1964. -296с.

9. Барчукова Ф.М. и др. Алгебра в 6-8-х классах под ред. Тихонова А. Н—М: Просвещение, 1988. -382с.

10. Бертран Ж. Алгебра для гимназий и реальных училищ. —С.Пб.: изд. И.И. Билибин 1885. -725с.

11. Билибин Н.И. Учебник алгебры для гимназий и реальных училищ. — ' С.Пб.: изд.И.И. Билибин. 1905. -502с.

12. Блонский П.П. Память и мышление. —M.-J1.: ГосСоцЭкИзд, 1935. -214с.

13. Богоявленский Д.Н., Менчинская Н. А. Психология усвоения знаний в школе. —М.: АПН РСФСР, 1959. -347с.

14. Божович Е.Д. Психологические особенности развития личности подростка. —М.: Знание, 1979. -39с.

15. Брадис В.М. Методика преподавания математики в средней школе. — М.: Учпедгиз, 1954. -504с.

16. Брунер Дж. Процесс обучения, —М.: АПН РСФСР, 1962. -84с.

17. Бычков Б.П. Международное движение за реформу преподавания математики в средней школе. —Кишинев: Штиинца, 1975. -135с.

18. Виноградов С.П. Повторительный курс алгебры. —М.: Тип. И.Д. Сытина, 1914. -299с.

19. Волков А. Проекты новых программ преподавания математики в средней школе, составленные Комиссией при Министерстве Народного просвещения весною 1915 года. //Математическое образование, -1916. - №1-2

20. Выготский JI.C. Избранные психологические произведения —М.: АПН РСФСР, 1956. -519с.

21. Глаголев А.Н. Элементарная алгебра. — М.: Тип. И.Д. Сытина: 1907. -319 с.

22. Гусев В.А., Мордкович А.Г. Математика. Справочные материалы. — М.: Просвещение, 1990. -416с.

23. Депман И.Я. Русские математические журналы для учителя. //Математика в школе. —М.: 1951. -№6 -96с.

24. Директивы ВКП(б) и постановления Советского правительства о народном образовании за 1917-1947 г.г.—М.-Л.: АПН РСФСР, 1947. -Вып.1 -320с.

25. Днепров Э.Д. Четвёртая школьная реформа в России. —М.: Интер-пракс, 1994. -241с.

26. Доклад Комиссии, избранным Московским математическим кружком, для рассмотрения проекта программ по математике, выработанного Комиссией при Министерстве Народного Просвещения. // Математическое образование.—М.: 1916. -№4-101-132с.

27. Долгушин П.А. Систематический курс алгебры для средних учебных заведений. —Петербург-Киев: Сотрудник, 1913. -220с.

28. Единая трудовая школа. Программы. —Минск, 1919. -148с.-185

29. Извольский Н. Приступим к свободной созидательной работе. //Математический вестник—М.; 1917. -Вып.2-33-64с.

30. Киселёв А.П. Алгебра. —Харьков-Киев: Радянська школа, 1934. -111с.

31. Киселёв А.П. Элементарная алгебра. — М.: Изд. Авт., 1888. -140с.

32. Колмогоров А.Н. О профессии математика. —М.: АПН РСФСР, 1959.30с.

33. Колягин Ю.М. Русская школа и математическое образование. —Орёл, 1996. -190с.

34. Концепция структуры и содержания общего среднего образования (в 12-летней школе). Проект. /ОВД Межведомственный информационный бюллетень. -М., 2000 -№9 -104с.

35. Крутецкий В.А. Психология обучения и воспитания школьников. —М.: Просвещение, 1976. -300с.

 

Скачано с www.znanio.ru