Справочный материал по теме "Линейная функция и ее график"

ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК

Теоретический материал

Функция – это зависимость y от x.

x – независимая переменная или аргумент функции.

y – зависимая переменная или значение функции.

Линейная функция – это функция вида .

Буквенные множители  и  – это числовые коэффициенты.

Вместо k и m могут стоять любые числа (положительные, отрицательные или дроби).

Коэффициент  – угловой коэффициент. Он всегда записывается перед  .

Коэффициенты  присутствуют в функции вида  всегда. Только в некоторых случаях они могут равняться нулю.

Примеры линейной функции и их коэффициенты:

Графиком линейной функции  является прямая.

Функция  называется линейной, так как ее графиком является прямая линия.

Чтобы построить график функции вида , достаточно будет построить на координатной плоскости всего две точки и провести через них прямую.

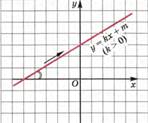
Если , то линейная функция возрастает.

Если двигаться по графику этой функции слева направо, то ординаты точек графика все время увеличиваются, мы как бы «поднимаемся в гору».

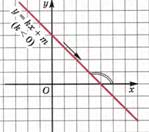
Если , то линейная функция убывает.

Если двигаться по графику этой функции слева направо, то ординаты точек графика все время уменьшаются, мы как бы «спускаемся с горы».

Практический материал

Задания, решаемые без построения графика функции

Задание 1.

Линейная функция задана формулой . Найти значение линейной функции, если значение ее аргумента равно:  а) 3;   б)  – 5.

Решение:

а) Аргумент – это переменная , т.е. имеем . Необходимо вычислить значение y при  Для этого достаточно подставить в функцию вместо x данное числовое значение.

Образец записи:

б) Аналогично рассуждая, получим, что необходимо вычислить значение y при  Для этого достаточно подставить в функцию вместо x данное числовое значение.

Образец записи:

Ответ: 

Задание 2.

Найти значение аргумента, при котором линейная функция принимает значение,  равное – 15,5.

Решение:

Значение функции – это значение , т.е. имеем . Необходимо найти значение , при котором  Для этого подставим в функцию вместо y  данное числовое значение.  Получим:

А это линейное уравнение с одной переменной, которое решается по правилам решения линейных уравнений.

Ответ:   при 

Задание 3.

Не выполняя построения, ответьте на вопрос: какая из точек принадлежит графику функции :         

Решение:

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (т.е. абсциссу точки вместо x и ее ординату вместо y).

Если получится верное равенство, значит, точка принадлежит функции, а если равенство неверное, то точка не принадлежит графику.

а) Подставим в функцию  координаты точки . Вместо x подставим 5, а вместо y подставим –7.

  (верно)

У нас получилось верное равенство, значит, точка с координатами  принадлежит заданной функции.

б) Подставим в функцию  координаты точки . Вместо x подставим 1, а вместо y подставим 2.

  (неверно)

У нас получилось неверное равенство, значит, точка с координатами  не принадлежит заданной функции.

        Ответ: точка , точка  не принадлежит.

Задание 4.

Найти координаты точек пересечения графика функции  с осями координат.

Решение:

Чтобы найти координаты точки пересечения графика функции с осью Oy (осью ординат) нужно:

• приравнять координату точки по оси Ox к нулю (x = 0);
• подставить вместо x в формулу функции ноль и найти значение y;
• записать полученные координаты точки пересечения с осью Oy.

Подставим вместо x в формулу функции число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) – координаты точки пересечения графика функции  c осью Oy.

Чтобы найти координаты точки пересечения графика функции с осью Ox (осью абсцисс) нужно:

• приравнять координату точки по оси Oy к нулю (y = 0);
• подставить вместо y в формулу функции ноль и найти значение x;
• записать полученные координаты точки пересечения с осью Oy.

Подставим вместо y в формулу функции  число ноль.

(2; 0) – координаты точки пересечения графика функции c осью Ox.

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните «правило противоположности».

а)     Если нужно найти координаты точки пересечения графика с осью Ox, то приравниваем y к нулю.

б)    Если нужно найти координаты точки пересечения графика с осью Oy, то приравниваем x к нулю.

Ответ: (0; 3) и (2; 0)

Задания, связанные с  построением графика функции

Задание 5.

Построить график линейной функции:   а)  

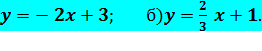
Решение:

Чтобы построить график функции вида , нам достаточно будет найти всего две точки.

а) Построим график функции Найдем значение функции y для двух произвольных значений x. Если коэффициент , стоящий перед x, является целым числом, то удобнее всего подставить вместо x числа 0 и 1.

Произведем расчеты:

Полученные значения x и y – это координаты точек графика функции. Их удобнее всего записывать в таблицу значений функции:

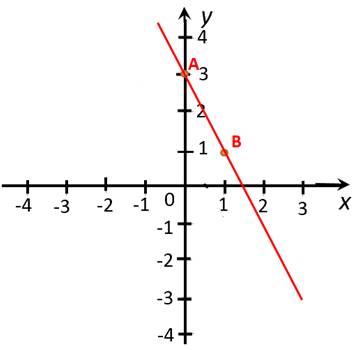
Отметим полученные точки на системе координат.

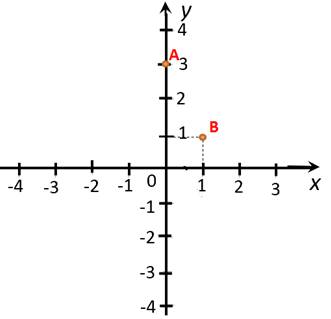Теперь проведем прямую через отмеченные точки. Эта прямая и будет являться графиком функции .

б) Построим график функции 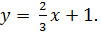Найдем значение функции y для двух произвольных значений x. Если коэффициент , стоящий перед x, является дробным числом, то удобнее всего подставить вместо x или 0, или числа, при умножении которых на   получится целое число.

Произведем расчеты:

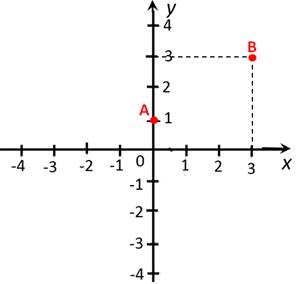
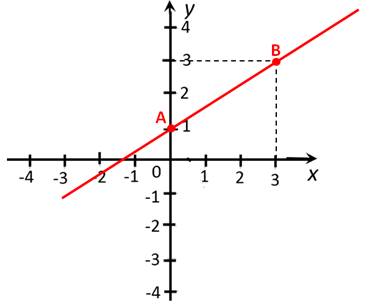
Полученные значения x и y записываем в таблицу значений функции:

Задание 6.

Построить график функции . Найти по графику:

а)    значение y соответствующее значению x, равному:   −1;  2;  3;  5;

б)    значение x, если значение y равно:  1;   4;   0;   −1.

Решение:

Построим сначала график функции

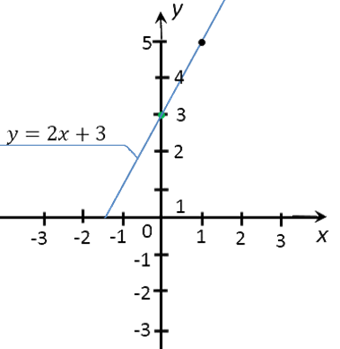
а) Чтобы найти значение y по известному значению x на графике функции необходимо:

1. 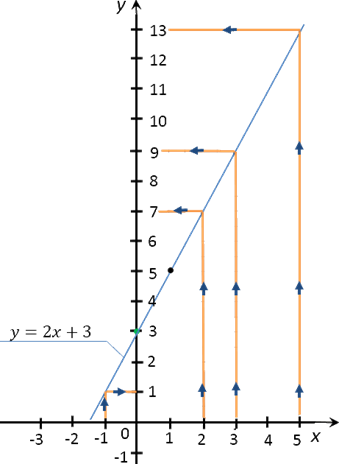    провести перпендикуляр от оси Ox из заданного числового значения x до пересечения с графиком функции;

2.     из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси Oy;

3.     полученное числовое значение на оси Oy и будет искомым значением.

Запишем полученные результаты:

б) Переходим ко второму заданию задачи. Требуется найти значение x, если значение y равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания. Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси Oy.

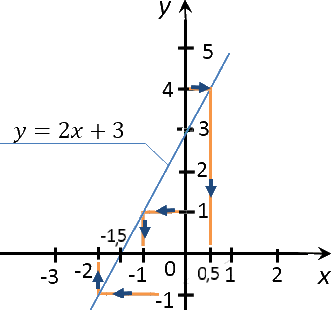
Запишем полученные результаты:

если , то ;                          если , то ;

если , то                        если , то .

Задание 7.

Найти координаты точек пересечения графика функции  с осями координат.

Решение:

Для начала построим график функции   и на графике отметим точки пересечения с осями.

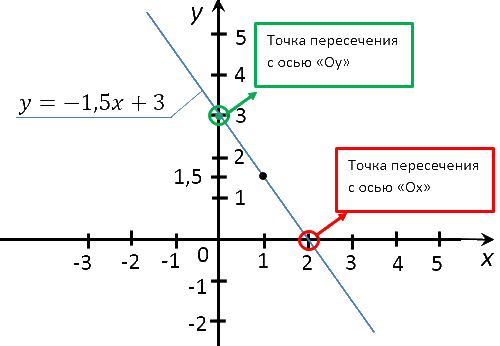
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции. Получили:

(0; 3) – координаты точки пересечения графика функции  c осью Oy.

(2; 0) – координаты точки пересечения графика функции c осью Ox.

Ответ: (0; 3) и (2; 0)

Задание 8.

Найти наибольшее и наименьшее значения для линейной функции :

а)  на отрезке ;

б)  на интервале ;

в)  на полуинтервале;

г)   на луче ;

д)  на луче

Решение:

Построим на координатной плоскости  график линейной функции . Выберем для  значения, указанные в задании:  и .

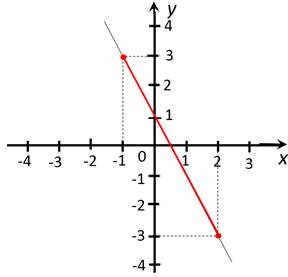Нам нужно рассмотреть эту линейную функцию не целиком, а на промежутках, указанных в задании.

а)   наибольшее и наименьшее значения на отрезке :

Самая большая ордината у точек, принадлежащих выделенной части, равна 3 – это и есть наибольшее значение линейной функции на отрезке :

Самая маленькая ордината у точек, принадлежащих выделенной части, равна –3

– это и есть наибольшее значение линейной функции на отрезке :

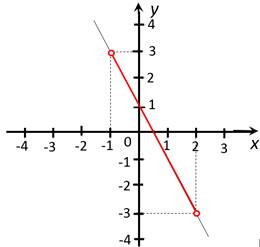
б)  наибольшее и наименьшее значения на полуинтервале :

В отличие от предыдущего случая, оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, из рассмотрения исключены. Значит, ни наибольшего, ни наименьшего значений на заданном интервале у данной функции нет.

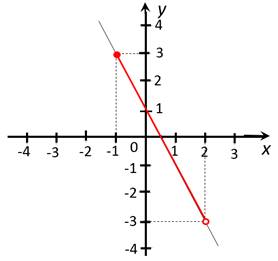
в)   наибольшее и наименьшее значения на интервале :

С помощью рисунка заключаем, что

  (как и в первом случае), а наименьшего значения у линейной функции нет (как во втором случае)

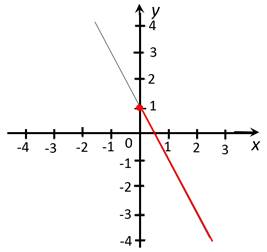
г)   наибольшее и наименьшее значения на луче :

 (этого значения линейная функция достигает при ), а  не существует.

д) 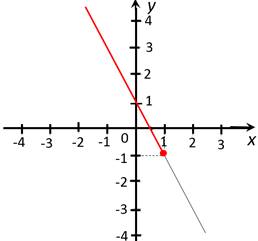 наибольшее и наименьшее значения на луче :

 (этого значения линейная функция достигает при ), а  не существует.

Скачано с www.znanio.ru