Тема 8. Использование средств Поиск решения.

Задания для самостоятельного выполнения:

№8.1.

Из круглой жестянки радиуса R изготавливается коническое пожарное ведро (рис.8.4.)

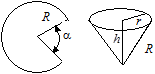
Рис.8.4. Образец изготовления конического пожарного ведра

Технология изготовления: из жестянки вырезается сектор с углом a, а остальная часть сворачивается в конус. Получается конус с высотой h и радиусом основания r. И высота h получившегося конуса и радиус его основания r зависят от радиуса заготовки R и угла a:

Радиус жестянки, из которой делается ведро R = 40 см.  Найдите при каком угле a объём V пожарного ведра будет максимальным.

V_конуса = pr²h/3

№8.2.

Найдите диаметр D и высоту H цилиндрической консервной банки объёмом     V = 500 см³,  при которых минимальна площадь её поверхности S.

Для справки:

S_пов-ти = 2*S_{основания}+S_{бок. пов-ти} = (pD²)/2 + pDH;

V = H*(pD²)/4

№8.3.

Найдите диаметр D и высоту H цилиндрической консервной банки объёмом     V = 500 см³, при которых минимальна суммарная длина L швов банки: L=2*pD+H;

V=H*(pD²)/4

№8.4

Найдите x и y, при которых значение f(х,у) будет минимальным:

f(x,y)=–2x–6y+x²–2xy+2y²

Необходимо учесть четыре ограничения:  x³0,   y³0,   x+y£2,   2y–x£2.

№8.5.

Найдите x и y, при которых значение f(х,у) будет наименьшим:

f(x,y)=x²+(y–4)²

Необходимо учесть два ограничения:   y–x–2£0,    2y–x²³0.

№8.6.

У квадратной жестянки со стороной  1м по углам вырезаются четыре квадрата со стороной  x (рис. 8.5.).

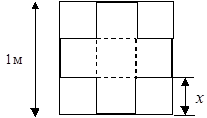
Рис.8.5. Образец заготовки

Затем полученная таким образом крестообразная заготовка сгибается по  пунктирным линиям в коробку без крышки (прямоугольный параллелепипед).

Найдите при каком x объём коробки будет максимальным.

V_{коробки} = x* (1–2*x)²

№8.7.

Найдите радиус основания r и высоту конуса h, при которых конус с объёмом V = 0,05 м³   будет иметь минимальную боковую поверхность S.

;   

V_конуса =  pr²h/3

№8.8.

На прямоугольном дорожном указателе шириной b и высотой h должно быть прямоугольное изображение площадью 1,5 м². По нижней стороне указатель имеет поле 0,2 м, а по трём остальным – 0,1 м (рис. 8.6.). Найдите значения b и h, при которых площадь указателя будет наименьшей.

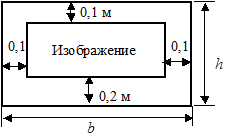
Рис.8.6. Образец указателя

№8.9.

Картонная коробка, имеющая форму прямоугольного параллелепипеда с размерами сторон a, b и c, должна иметь объём 1 м³. Определите, какими должны быть размеры, чтобы площадь поверхности коробки была минимальной, если размер b не должен быть меньше 1,5 м.

S_{пов-ти коробки} = 2ac+2bc;

V = abc

№8.10.

Монета, имеющая форму цилиндра, должна иметь определённую массу (определённый объём). Отношение высоты монеты к диаметру должно быть не более 0,1 и не менее 0,06. Определите диаметр и высоту монеты, объёмом 0,5 см³, при которых площадь поверхности монеты будет минимальной.

S_пов-ти = 2*S_{основания}+S_{бок. пов-ти} = (pD²)/2 + pDH;

V = H*(pD²)/4

Скачано с www.znanio.ru