3.               СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМ НА ЭВМ. СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

В практике моделирования систем информатики наиболее часто приходится иметь дело с объектами, которые в процессе своего функционирования содержат элементы стохастичности или подвергаются стохастическим воздействиям внешней среды. Поэтому основным методом получения результатов с помощью имитационных моделей таких стохастических систем является метод статистического моделирования на ЭВМ, использующий в качестве теоретической базы предельные теоремы теории вероятностей. Возможность получения пользователем модели результатов статистического моделирования сложных систем в условиях ограниченности машинных ресурсов существенно зависит от эффективности процедур генерации псевдослучайных последовательностей на ЭВМ, положенных в основу имитации воздействий на элементы моделируемой системы. 

3.1.              Стохастические системы и возможности их компьютерного моделирования 

Дискретно-стохастические модели. Основные соотношения  

В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. 

Применение схем вероятностных автоматов (Р-схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворящих заданным ограничениям.

Введем математическое понятие Р-автомата, рассмотрим множество G, элементами которого являются всевозможные пары (x_i, z_s), где x_i  и  z_s — элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции φ и ψ то с их помощью осуществляются отображения G→Z и G→Y, то говорят, что F = ‹Z, X, Y, φ, ψ› определяет автомат детерминированного типа. Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида (z_k, у_j), где y_j — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

       Элементы из Ф       …       (z₁, y₁)…        (x₁, y₂)…      …     (z_K, y_j-1)       (z_K, y_j)

                (x_b z_k)                …            b_1,1                  b_1,2           …       b_K(j-1)           b_Kj

 

                               K       J

При этом b_kj 1, где b_kj вероятности перехода автомата в

k 1 j 1

состояние z_k и появление на выходе сигнала y_j если он был в состоянии z_s и на его вход в этот момент времени поступил сигнал х_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = ‹Z, X, Y, В› называется вероятностным автоматом (Р-автоматом).

Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

 

Элементы из Y(x_i, z_s) …… y₁ q₁ y₂ q₂ …… y_3-1 q_3-1 y₃ q₃ Элементы из Z(x_i, z_s) …… z₁ z₁ z₂ z₂ …… z_K-1 z_K-1 z_K z_K

 

                                K                                J

При этом z_k 1 иq _j 1, где z_k и q_k — вероятности пере-

                               k1                            j1

хода Р-автомата в состояние z_k и появления выходного сигнала y_k при условии, чтоР-автомат находился в состоянии z_s, и на его вход поступил входной сигнал x_i.

Если для всех К и Y имеет место соотношение q_kZ_i = b_kJ, то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала. Пусть теперь определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества Y индуцирует:

 

              Элементы из Y_zK               ……      y₁s₁     y₂s₂     ……        y_K-1 s_I-1       y_Ks_I

 

I

Здесьs_i 1, где s_i — вероятность появления выходного сиг-

i1

нала у_i, при условии, что Р-автомат находился в состоянии z_k.

Возможные приложения   

Если для всех К и I имеет место соотношение z_ks_i = b_ki то такой Р-автомат называется вероятностным автоматом Мура. Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом, задаваемым P = ‹Z, X, Y, φ, ψ› Частным случаем Р-автомата, задаваемого как P = ‹Z, X, Y, B› являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно.

Если выходной сигнал Р-автомата определяется детерминированно, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-demepминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

Непрерывно-стохастические модели (Q-схемы)  

Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (англ. queueing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

Основные соотношения

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т. д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, то есть стохастический характер процесса их функционирования.

Остановимся на основных понятиях массового обслуживания, необходимых для использования Q-схем, как при аналитическом, так и при имитационном.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого i-го прибора обслуживания П_i (рис. 3.1.1), состоящего из накопителя заявок Н_i, в котором может одновременно нахо-

диться l_i  0,L_i^H заявок, где L_iH — емкость i-го накопителя, и канала обслуживания заявок (или просто канала) К_i. На каждый элемент прибора обслуживания П_i поступают потоки событий: в накопитель H_i — поток заявок wi, на канал K_i — поток обслуживании и_i.

Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуетсятолько моментами поступления этих событий (вызывающими моментами) и задается последовательностью:   t_n   0 t₁ t₂... t_n ..., где t_n— момент наступления n-го события — неотрицательное вещественное число.

Однородный поток событий также может быть задан в виде последовательности промежутков времени между n – m и (n – 1) – м событиями {τ_n}, которая однозначно связана с последовательностью  вызывающих моментов {t_n}, где τ_n = t_n – t_n – t_n – 1, n≥1, t₀ = 0, т. е. τ₁ = t₁ 

Потоком неоднородных событий называется последовательность {t_n, f_n}, где t_n — вызывающие моменты; t_n — набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок могут бытьзаданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т. п.

 

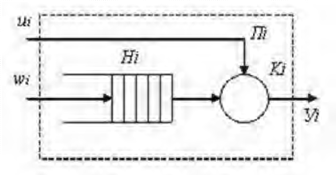
Рис. 3.1.1. Прибор обслуживания заявок 

Возможные приложения  

Обычно в приложениях при моделировании различных систем применительно к элементарному каналу обслуживания К_i, можно считать, что поток заявок w_iєW, то есть интервалы времени между моментами появления заявок (вызывающие моменты) на входе K_i образует подмножество неуправляемых переменных, а поток обслуживания u_iєU, то есть интервалы времени между началом и окончанием обслуживания заявки, образует подмножество управляемых переменных.

Заявки, обслуженные каналом К_i, и заявки, покинувшие прибор

П_i по различным причинам необслуженными (например, из-за переполнения накопителя H_i), образуют выходной поток y_iє Y, то есть. интервалы времени между моментами выхода заявок образуютподмножество выходных переменных.

 Процесс функционирования прибора обслуживания П_i можно представить как процесс изменения состояний его элементов во времени z_i (t). Переход в новое состояние для П_i означает изменение количества заявок, которые в нем находятся (в канале K_i и в накопителе H_i). Таким образом, вектор состояний для Пi имеет вид

urz_i z z_i^H , _i^K , где z_i H — состояние накопителя Hi, (z_iH = 0 — накопитель пуст, z_iH = 1 — в накопителе имеется одна заявка, ..., ziH = L_iH — накопитель полностью заполнен); L_iH — емкость накопителя H_i, измеряемая числом заявок, которые в нем могут поместиться; z_iK — состояние канала K_i (z_iK = 0 — канал свободен, z_iK = l — канал занят и т. д.).

В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания П_i (сети массового обслуживания). Если каналы K_i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы П_i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.

Связи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, то есть обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.  Собственными (внутренними) параметрами Q-схемы будут являться количество фаз L_ф, количество каналов в каждой фазе L_kj,

, количество накопителей каждой фазы L_Hk, k 1,L^ф емкость i-го накопителя L_iH. Следует отметить, что в теории массового обслуживания в зависимости от емкости накопителя применяют следующую терминологию для систем массового обслуживания: системы с потерями (L_iH =, то есть накопитель в приборе П_i, отсутствует, а имеется только канал обслуживания К_i), системы  с ожиданием (L_iH→∞, то есть накопитель H_i имеет бесконечную емкость и очередь заявок не ограничивается) и системы смешанного типа (с ограниченной емкостью накопителя H_i).Всю совокупность собственных параметров Q-схемы обозначим как подмножество Н.

 Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Н_i и обслуживания заявок каналом Ki каждого элементарного обслуживающего прибора П_i Q-схемы. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов.

 В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, то есть они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя H_i на обслуживание каналом K_i можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель H_i, ожидает окончания обслуживания предшествующей заявки каналом К_i и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н_i, прерывает обслуживание каналом К_i заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из K_i заявка может либо покинуть систему, либо может быть снова записана на какое-то место в H_i).

При рассмотрении алгоритмов функционирования приборов обслуживания П_i (каналов K_i и накопителей H_i необходимо также задать набор правил, по которым заявки покидают Н_i и К_i: для H_i — либо правила переполнения, по которым заявки в зависимости от заполнения H_i покидают систему, либо правила ухода, связанные с истечением времени ожидания заявки в H_i, для К_i — правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале K_i или не допускаются до обслуживания каналом К_i, то есть правила блокировок канала. При этом различают блокировки K_i по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q-схеме, регулирующих поток заявок в зависимости от состояний Q-схемы. Весь набор возможных алгоритмов поведения заявок в Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок  А.  

Таким образом, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается в виде Q = ‹W, U, H, Z, R, А›.

При ряде упрощающих предположений относительно подмножеств входящих потоков WVL потоков обслуживания U (выполнение условий стационарности, ординарности и ограниченного последействия) оператора сопряжения элементов структуры R (однофазное одноканальное обслуживание в разомкнутой системе), подмножества собственных параметров Н (обслуживание с бесконечной емкостью накопителя), оператора алгоритмов обслуживания заявок А (бесприоритетное обслуживание без прерываний и блокировок) для оценки вероятностно-временных характеристик можно использовать аналитический аппарат, разработанный в теории массового обслуживания. При принятых предположениях в обозначениях Д. Кендалла будет иметь место классическая система обслуживания типа М/М/1 (одноканальная система с марковским входящим потоком заявок и марковским потоком обслуживания). Рассмотрим на примере основные аналитические соотношения для такой элементарной Q-схемы.

3.2.  Датчики случайных чисел. Метод Монте-Карло 

Метод Монте-Карло

Специальный метод изучения поведения заданной статистики при проведении многократных повторных выборок, существенно использующий вычислительные возможности современных компьютеров. При проведении анализа по методу Монте-Карло компьютер использует процедуру генерации псевдослучайных чисел для имитации данных из изучаемой генеральной совокупности. Процедура анализа по методу Монте-Карло модуля Моделирование структурными уравнениями строит выборки из генеральной совокупности в соответствии с указаниями пользователя, а затем производит следующие действия, для каждого повторения по методу Монте-Карло:

1.  Имитирует случайную выборку из генеральной совокупности. 

2.  Проводит анализ выборки.

3.  Сохраняет результаты. 

После большого числа повторений, сохраненные результаты хорошо имитируют реальное распределение выборочной статистики. Метод Монте-Карло позволяет получить информацию о выборочном распределении в случаях, когда обычная теория выборочных распределений оказывается бессильной.

На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины £ используются формулы (алгоритмы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными. Требования к генератору случайных чисел 

Прежде чем перейти к описанию конкретных алгоритмов получения на ЭВМ последовательностей псевдослучайных чисел, сформулируем набор требований, которым должен удовлетворять идеальный генератор. Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных чисел находят алгоритмы вида:

 X_i + 1 = Ф(x_i)                          (3.2.1) 

представляющие собой рекуррентные соотношения первого порядка, для которых начальное число х₀ и постоянные параметры заданы.

Например, легко показать, что функция вида (3.2.1),  не может породить хорошую последовательность псевдослучайных чисел х₁, х₂, ... Действительно, если построить точки с координатами (x₁, x₂), (х₃, x₄) по случайным числам, полученная случайными числами, то они будут равномерно распределены в единичном квадрате 0 ≤ x_i ≤ 1, 0 ≤ x_i+1 ≤ 1. Соответствующие же точки, построенные по числам (x₁,Ф(x₂)), (х₃, Ф(х₄)),… располагаются в площади, ограниченной кривой х_i + 1 = Ф (x_i).

Хорошую последовательность случайных чисел может породить только такая функция х_i + 1 = Ф (x₁), график которой достаточно плотно заполняет единичный квадрат. Примером такой функции может служить x_i + 1 = Д(Ax_i) при больших целых положительных А, где Д(и) = и – Ц(и) — дробная часть числа и; Ц(и) — целая часть числа и, то есть наибольшее целое число, не превосходящее и. Пусть для примера А = 10, тогда функция х_i + 1 = Ф(х_i) будет иметь другой вид, приведенные условия являются только необходимыми, но не достаточными для того, чтобы соотношение (3.2.1) порождало хорошие последовательности псевдослучайных чисел. 

3.3.    Имитация случайных событий при имитационных экспериментах со стохастическими системами 

Статистическое моделирование системы — один из основных, учитывающий стохастические воздействия. Количество случайных чисел, используемых для получения статистически устойчивой оценки характеристики процесса функционирования системы S, при реализации моделирующего алгоритма на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. 

Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно и большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества исходных (базовых) последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования, последовательностей случайных чисел требуемого качества во многом определяет возможность практического использования машинного моделирования систем.

Рассмотрим возможности и особенности получения последовательностей случайных чисел при статистическом моделировании систем на ЭВМ. На практике используются три основных способа генерации случайных чисел: аппаратный (физический), табличный (файловый) и алгоритмический (программный). Аппаратный способ   

При этом способе генерации случайные числа вырабатываются специальной электронной приставкой — генератором (датчиком) случайных чисел, — служащей в качестве одного из внешних устройств ЭВМ. Таким образом, реализация этого способа генерации не требует дополнительных вычислительных операций ЭВМ по выработке случайных чисел, а необходима только операция обращения к внешнему устройству (датчику). В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т. д. 

Возможны и другие схемные решения аппаратных генераторов случайных чисел. Однако аппаратный способ получения случайных чисел не позволяет гарантировать качество последовательности непосредственно во время моделирования системы S на ЭВМ, а также повторно получать при моделировании одинаковые последовательности чисел.

Табличный способ  

Если случайные числа, оформленные в виде таблицы, помещать во внешнюю или оперативную память ЭВМ, предварительно сформировав из них соответствующий файл (массив чисел), то такой способ будет называться табличным. Однако этот способ получения случайных чисел при моделировании систем на ЭВМ обычно рационально использовать при сравнительно небольшом объеме таблицы и соответственно файла чисел, когда для хранения можно применять оперативную память. Хранение файла во внешней памяти при частном обращении в процессе статистического моделирования не рационально, так как вызывает увеличение затрат машинного времени при моделировании системы S из-за необходимости обращения к внешнему накопителю. Возможны промежуточные способы организации файла, когда он переписывается в оперативную память периодически по частям. Это уменьшает время на обращение к внешней памяти, но сокращает объем оперативной памяти, который можно использовать для моделирования процесса функционирования системы S.

Алгоритмический способ

Способ получения последовательностей случайных чисел основан на формировании случайных чисел в ЭВМ с помощью специальных алгоритмов и реализующих программ. 

Каждое случайное число вычисляется с помощью соответствующей программы по мере возникновения потребностей при моделировании системы на ЭВМ.

Таблица 3.3.1

Сравнительный анализ способов генерации случайных чисел

Способ	Достоинства	Недостатки
1	2	3
Аппаратный	Запас чисел не ограничен. Расходуется мало операций вычислительной машины. Не занимается место в памяти машины	Требуется периодическая проверка. Нельзя производить последовательность. Используется специальное устройство. Необходимы меры по обеспечению стабильности

Окончание табл. 3.3.1

1	2	3
Табличный	Требуется однократная проверка. Можно воспроизводить последовательность	Запас чисел. Занимает много места в оперативной памяти или необходимо время на обращение время к внешней памяти
Алгоритмический	Требуется однократная проверка. Можно многократно воспроизводить последовательность чисел. Занимает мало места в памяти машины. Не используются внешние устройства	Запас чисел последовательности ограничен ее периодом. Существенные затраты машинного времени

Достоинства и недостатки трех перечисленных способов получения случайных чисел для сравнения представлены в табл. 3.3.1. Из этой таблицы видно, что алгоритмический способ получения случайных чисел наиболее рационален на практике при моделировании систем на универсальных ЭВМ.

3.4.  Общая характеристика СМО-моделирования на ЭВМ 

В терминах систем массового обслуживания (СМО) описываются многие реальные системы: вычислительные системы, узлы сетей связи, системы посадки самолетов, магазины, производственные участки, любые системы, где возможны очереди и (или) отказы в обслуживании.

В вычислительной системе роль обслуживающего прибора играет ЭВМ — роль заявок, решаемые задачи. Источником заявок служат терминалы пользователей. Моментом выдачи заявки является момент нажатия клавиши для подачи директивы о запуске задачи на решение. Операционная системы ЭВМ исполняет роль диспетчера: определяет очередность решения задач. В роли ячеек буфера выступают ячейки памяти ЭВМ, хранящие сведения о задачах, требующих решения.

В системе разгрузки судна, другой пример реальной системы, источниками заявок являются направления, откуда прибывают суда. Момент выдачи заявки — это момент прибытия судна в зону морского порта для разгрузки/погрузки. Обслуживающим прибором является причал вместе с персоналом и техническими средствами, организующими разгрузку/погрузку. Роль буфера играет акватория порта. Усложнение структур и режимов реальных систем затрудняет применение классических методов теории массового обслуживания ввиду возрастающей размерности решаемых задач, что особенно характерно для систем с сетевой структурой. Одним из возможных путей преодоления размерности является использование моделей в форме сетей массового обслуживания (СеМО).

3.5.  Примеры систем и сетей массового обслуживания 

Сети массового обслуживания

Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой. Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). При этом отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО, структуру системы, а требования, циркулирующие по СеМО, составляющие материальные потоки (сообщения (пакеты) в коммуникационной сети, задания в мультипроцессорных системах, контейнеры грузопотоков и т. п.).

Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным СМО, а дуги отображают связи между узлами.

Переход заявок между узлами происходит мгновенно в соответствии с переходными вероятностями P i j_ij , , 1,N , p_ij, вероятность того, что заявка после обслуживания в узле i перейдет в узел j. Естественно, если узлы непосредственно не связаны между собой, то p_ij = 0. Если из i‐го узла переход только в один какой-либо узел j, то p_ij = 1.

СеМО классифицируют по нескольким признакам (рис. 3.5.1). 

 

Сеть называется линейной, если интенсивности потоков заявок в узлах связаны между собой линейной зависимостью 

lj = aijli,

где a_ij — коэффициент пропорциональности, или относительно источника

l_j = a_ijl₀.

Коэффициент a_j называют коэффициентом передачи, он характеризует долю заявок, поступающих в j‐й узел от источника заявок, либо — среднее число прохождений заявкой через данный узел за время нахождения заявки в сети.

Если интенсивности потоков заявок в узлах сети связаны нелинейной зависимостью (например, λ _j  a_jλ₀ ), то сеть называется нелинейной.

Сеть всегда линейна, если в ней заявки не теряются и не размножаются.

Разомкнутая сеть — это такая отрытая сеть, в которую заявки поступают из внешней среды и уходят после обслуживания из сети во внешнюю среду. Другими словами, особенностью разомкнутой СеМО (РСеМО) является наличие одного или нескольких независимых внешних источников, которые генерируют заявки, поступающие в сеть, независимо от того, сколько заявок уже находится в сети. В любой момент времени в РСеМО может находиться произвольное число заявок (от 0 до ¥).

В замкнутой СеМО (ЗСеМО) циркулирует фиксированное число заявок, а внешний независимый источник отсутствует. Исходя из физических соображений, в ЗСеМО выбирается внешняя дуга, на которой отмечается псевдонулевая точка, относительно которой могут измеряться временные характеристики.

Комбинированная сеть — это сеть, в которой постоянно циркулирует определенное число заявок и есть заявки, поступающие от внешних независимых источников.

В однородной сети циркулируют заявки одного класса. И, наоборот, в неоднородной сети могут присутствовать заявки нескольких классов. Заявки относятся к разным классам, если они различаются хотя бы одним из следующих атрибутов: 

•       законом распределения длительности обслуживания в узлах; 

•       приоритетами; 

•       маршрутами (путями движения заявок в сети). 

 

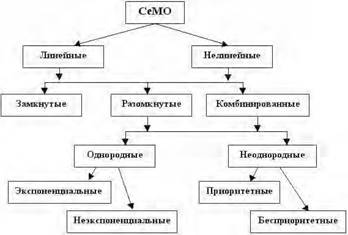
Рис. 3.5.1. Классификация сетей массового обслуживания

В экспоненциальной сети длительности обслуживания во всех узлах распределены по экспоненциальному закону, и потоки, поступающие в разомкнутую сеть, простейшие (пуассоновские). Во всех остальных случаях сеть является неэкспоненциальной.

Если хотя бы в одном узле осуществляется приоритетное обслуживание, то это — приоритетная сеть. Приоритет — это признак, определяющий очередность обслуживания. Если обслуживание заявок в узлах осуществляется в порядке поступления, то такая сеть бесприоритетная.

Таким образом, экспоненциальной будем называть СеМО, отвечающую требованиям: 

•       входные потоки СеМО пуассоновские; 

•       во всех N СМО время обслуживания заявок имеет экспоненциальную функцию распределения вероятностей, и заявки обслуживаются в порядке прихода; 

•       переход заявки с выхода i-й СМО на вход j-й является независимым случайным событием, имеющим вероятность

P_ij i j, 1,N ; P_i0  вероятность ухода заявки из CeМО.

Если заявки приходят в сеть и уходят из нее, то сеть называется разомкнутой. Если заявки не приходят в сеть и из нее не уходят, сеть называется замкнутой. Число заявок в замкнутой сети постоянное.

Системы  массового обслуживания 

Понятие о задачах теории массового обслуживания.

Многие экономические организации и системы, получающие прибыль за счет обслуживания клиентов, можно достаточно точно описать с помощью совокупности математических методов и моделей, которые получили название теории массового обслуживания (ТМО). 

С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания. Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.

Очереди возникают практически во всех системах массового обслуживания (CМО) и теория массового обслуживания (теория очередей) занимается оценкой функционирования системы при заданных параметрах и поиском параметров, оптимальных по некоторым критериям. 

Эта теория представляет особый раздел теории случайных процессов и использует, в основном, аппарат теории вероятностей. Первые публикации в этой области относятся к 20-м годам XX века и принадлежат датчанину А. Эрлангу, занимавшемуся исследованиями функционирования телефонных станций — типичных СМО, где случайны моменты вызова, факт занятости абонента или всех каналов, продолжительность разговора. В дальнейшем теория очередей нашла развитие в работах К. Пальма, Ф. Поллачека, А.Я. Хинчина, Б.В. Гнеденко, А. Кофмана, Р. Крюона, Т. Cаати и других отечественных и зарубежных математиков. 

В качестве основных элементов СМО следует выделить входной поток заявок, очередь на обслуживание, cистему (механизм) обслуживания и выходящий поток заявок. В роли заявок (требований, вызовов) могут выступать покупатели в магазине, телефонные вызовы, поезда при подходе к железнодорожному узлу, вагоны под разгрузкой, автомашины на станции техобслуживания, самолеты в ожидании разрешения на взлет, штабель бревен при погрузке на автотранспорт. Роль обслуживающих приборов (каналов, линий) играют продавцы или кассиры в магазине, таможенники, пожарные машины, взлетно-посадочные полосы, экзаменаторы, ремонтные бригады.

 

Рис. 3.5.2. Пример СМО

В зависимости от характеристик этих элементов СМО классифицируются следующим образом. 

По характеру поступления заявок. Если интенсивность входного потока (количество заявок в единицу времени) постоянна или является заданной функцией от времени, поток называют регулярным. Если параметры потока независимы от конкретного момента времени, поток называют стационарным. 

По количеству одновременно поступающих заявок. Поток с вероятностью одновременного появления двух и более заявок равной нулю называется ординарным. 

 По связи между заявками. Если вероятность появления очередной заявки не зависит от количества предшествующих заявок, имеем дело с потоком без последействия. 

По однородности заявок выделяют однородные и неоднородные потоки. 

По ограниченности потока заявок различают замкнутые и разомкнутые системы (система с ограниченной клиентурой называется замкнутой). Так универсальный магазин является разомкнутой системой, тогда как оптовый магазин с постоянными клиентами — замкнутая система. 

По поведению в очереди системы делятся на системы с отказами (заявка покидает систему, если нет мест в очереди), c ограниченным ожиданием и с ожиданием без ограничения времени. 

По дисциплине выбора на обслуживание. Здесь можно выделить системы с обслуживанием в порядке поступления, в случайном порядке, в порядке, обратном поступлению (последний пришел — первым обслужен) или с учетом приоритетов. 

По числу каналов обслуживания системы разделяют на одно — и многоканальные. 

По времени обслуживания выделяют системы с детерминированным и случайным временем. 

По количеству этапов обслуживания различают однофазные и многофазные системы. 

3.6.            Аналитические методы расчета характеристик пуассоновских СМО 

Методы моделирования информационных сетей 

Система массового обслуживания  одна из основных моделей, используемых инженерами-системотехниками. Как модель, СМО рассматривается в теории массового обслуживания (другое название — теория очередей). Первые работы в этой области были вызваны потребностями практики, в частности широким развитием телефонных сетей. Поэтому в работах по теории СМО широко используется терминология, заимствованная из телефонии: требования, вызовы, заявки, каналы (приборы) обслуживания и т. п. 

Теория массового обслуживания связана с разработкой и анализом математических, то есть абстрактных, моделей, которые описывают процесс обслуживания некоторых объектов, поступающих на вход обслуживающего прибора в виде некоторого потока, и образующего в общем случае очередь на входе обслуживающего прибора. 

Поскольку рассматриваются абстрактные модели, совершенно не важна природа обслуживаемых объектов и их физические свойства (будь то вызовы, управляющие или информационные кадры в сети связи или посетители магазина, или детали на автоматической линии и т. п.). Существенным являются моменты появления этих объектов и правила, и законы (математические) их обслуживания, так как от этих моментов и законов зависит адекватное отображение эволюции моделируемого объекта во времени. Поэтому, когда говорят о методах анализа очередей, имеют в виду математические (абстрактные) модели, а из контекста всегда должно быть ясно, для исследования какой реальной системы применяются эти модели. 

Целью использования СМО (как модели) является анализ качества функционирования указанных систем-оригиналов. 

В свою очередь, СеМО используют для определения важнейших системных характеристик информационных систем: производительности; времени доставки пакетов; вероятности потери сообщений и блокировки в узлах; области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания и др. В теории СеМО фундаментальным является понятие состояния сети. Важнейшая характеристика сетей МО  вероятности их состояний. Для определения вероятностей состояний СеМО исследуют протекающий в сети случайный процесс. В качестве моделей протекающих в СеМО процессов наиболее часто используют марковские и полумарковские. 

Марковским процессом с непрерывным временем описывают функционирование экспоненциальных СеМО. Сеть называется экспоненциальной, если входящие потоки требований в каждую СМО пуассоновские, а времена каждого этапа обслуживания, реализуемого на любой СМО-сети, имеют экспоненциальное распределение. Это позволяет считать, что этапы обслуживания независимы между собой и не зависят ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования требований. 

Теория экспоненциальных СеМО наиболее разработана, и ее широко применяют как для исследования сетей ПД так и для исследования мультипроцессорных вычислительных систем (ВС). Разработаны практические формы расчета вероятностновременных характеристик (ВВХ) таких сетей и систем. 

Попытки глубокого анализа немарковских моделей сетевых систем наталкиваются на значительные трудности, которые обусловлены в частности отсутствием независимости длительностей пребывания требований в различных узлах моделей сетевых систем с нестандартными дисциплинами. Так например, при достаточно реалистическом предположении о том, что длина требования остается постоянной в процессе его передачи через узлы сети, необходимо прослеживать путь каждого требования, что делает невозможным аналитический расчет характеристики для сети с числом узлов М>2. 

Анализ работ, посвященных исследованию или расчету немарковских моделей, показывает, что решения, как правило, получены алгоритмически путем сложных численных расчетов с использованием преобразований Лапласа-Стилтьеса, реализуются программно, отличаются большой трудоемкостью, либо значительными погрешностями в оценке показателей производительности информационных систем (ИС) в области средней и большой нагрузки. Поэтому для моделирования СеМО, выходящих из класса мультипликативных, используют приближенные методы. 

Сравнительный анализ приближенных методов моделирования СеМО и примеры показывают, что пользоваться приближенными методами расчета СеМО необходимо с большой осторожностью, что при расчете конкретных СеМО в процессе решения различных прикладных задач представляется необходимым проведение исследований в целях оценки точности и чувствительности применяемого метода, а также проведение эксперимента по имитационному моделированию исходной СеМО для достаточно большого множества значений варьируемых параметров. 

Таким образом, аналитические методы расчета характеристик ИС базируются, как правило, на анализе экспоненциальных СеMO. При использовании этого математического аппарата удается получить аналитические модели для решения широкого круга задач исследования систем. 

CеМО — это, прежде всего, совокупность взаимосвязанных систем массового обслуживания. Поэтому необходимо вспомнить основные особенности этих систем. 

3.7. Моделирование потоков заявок в реальных системах. Моделирование станций обслуживания и очередей 

Большой класс систем, которые сложно изучить аналитическими способами, но которые хорошо изучаются методами статистического моделирования, сводится к системам массового обслуживания (СМО). 

В СМО подразумевается, что есть типовые пути (каналы обслуживания), через которые в процессе обработки проходят заявки. Принято говорить, что заявки обслуживаются каналами. Каналы могут быть разными по назначению, характеристикам, они могут сочетаться в разных комбинациях; заявки могут находиться в очередях и ожидать обслуживания. Часть заявок может быть обслужена каналами, а части могут отказать в этом. Важно, что заявки, с точки зрения системы, абстрактны: это то, что желает обслужиться, то есть пройти определенный путь в системе. Каналы являются также абстракцией: это то, что обслуживает заявки. 

Заявки могут приходить неравномерно, каналы могут обслуживать разные заявки за разное время и так далее, количество заявок всегда весьма велико. Все это делает такие системы сложными для изучения и управления, и проследить все причинноследственные связи в них не представляется возможным. Поэтому принято представление о том, что обслуживание в сложных системах носит случайный характер. 

Примерами СМО (см. табл. 3.7.1) могут служить: автобусный маршрут и перевозка пассажиров; производственный конвейер по обработке деталей; влетающая на чужую территорию эскадрилья самолетов, которая «обслуживается» зенитками ПВО; ствол и рожок автомата, которые «обслуживают» патроны; электрические заряды, перемещающиеся в некотором устройстве и т. д. 

Таблица 3.7.1

Примеры систем массового обслуживания

СМО	Заявки	Каналы
Автобусный маршрут и перевозка пассажиров	Пассажиры	Автобусы
Производственный конвейер по обработке деталей	Детали, узлы	Станки, склады
Влетающая на чужую территорию эскадрилья самолетов, которая «обслуживается» зенитками ПВО	Самолеты	Зенитные орудия, радары, стрелки, снаряды
Ствол и рожок автомата, которые «обслуживают» патроны	Патроны	Ствол, рожок
Электрические заряды, перемещающиеся в некотором устройстве	Заряды	Каскады технического устройства

 

Но все эти системы объединены в один класс СМО, поскольку подход к их изучению един. Он состоит в том, что, во-первых, с помощью генератора случайных чисел разыгрываются случайные числа, которые имитируют СЛУЧАЙНЫЕ моменты появления заявок и время их обслуживания в каналах. Но в совокупности эти случайные числа, конечно, подчинены статистическим закономерностям. 

К примеру, пусть сказано: «заявки в среднем приходят в количестве 5 штук в час». Это означает, что времена между приходом двух соседних заявок случайны, например: 0.1; 0.3; 0.1; 0.4; 0.2, как это показано на рис. 3.7.1, но в сумме они дают в среднем 1 (обратите внимание, что в примере это не точно 1, а 1.1 — но зато в другой час эта сумма, например, может быть равной 0.9); и только за достаточно большое время среднее этих чисел станет близким к одному часу. 

 

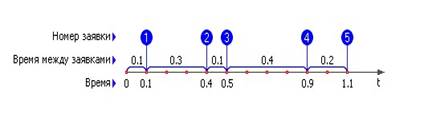
Рис. 3.7.1. Случайный процесс прихода заявок в СМО 

Результат (например, пропускная способность системы), конечно, тоже будет случайной величиной на отдельных промежутках времени. Но измеренная на большом промежутке времени, эта величина будет уже, в среднем, соответствовать точному решению. То есть для характеристики СМО интересуются ответами в статистическом смысле. 

Итак, систему испытывают случайными входными сигналами, подчиненными заданному статистическому закону, а в качестве результата принимают статистические показатели, усредненные по времени рассмотрения или по количеству опытов. 

Во-вторых, все модели СМО собираются типовым образом из небольшого набора элементов (канал, источник заявок, очередь, заявка, дисциплина обслуживания, стек, кольцо и так далее), что позволяет имитировать эти задачи типовым образом. Для этого модель системы собирают из конструктора таких элементов. Неважно, какая конкретно система изучается, важно, что схема системы собирается из одних и тех же элементов. Разумеется, структура схемы будет всегда различной. 

Перечислим некоторые основные понятия СМО 

Каналы — то, что обслуживает; бывают горячие (начинают обслуживать заявку в момент ее поступления в канал) и холодные (каналу для начала обслуживания требуется время на подготовку). Источники заявок — порождают заявки в случайные моменты времени, согласно заданному пользователем статистическому закону. Заявки, они же клиенты, входят в систему (порождаются источниками заявок), проходят через ее элементы (обслуживаются), покидают ее обслуженными или неудовлетворенными. Бывают нетерпеливые заявки — такие, которым надоело ожидать или находиться в системе и которые покидают по собственной воле СМО. Заявки образуют потоки — поток заявок на входе системы, поток обслуженных заявок, поток отказанных заявок. Поток характеризуется количеством заявок определенного сорта, наблюдаемым в некотором месте СМО за единицу времени (час, сутки, месяц), то есть поток есть величина статистическая. 

Очереди характеризуются правилами стояния в очереди (дисциплиной обслуживания), количеством мест в очереди (сколько клиентов максимум может находиться в очереди), структурой очереди (связь между местами в очереди). Бывают ограниченные и неограниченные очереди. Перечислим важнейшие дисциплины обслуживания. FIFO (First In, First Out — первым пришел, первым ушел): если заявка первой пришла в очередь, то она первой уйдет на обслуживание. LIFO (Last In, First Out — последним пришел, первым ушел): если заявка последней пришла в очередь, то она первой уйдет на обслуживание (пример — патроны в рожке автомата). SF (Short Forward — короткие вперед): в первую очередь обслуживаются те заявки из очереди, которые имеют меньшее время обслуживания. 

Пример, показывающий, как правильный выбор той или иной дисциплины обслуживания позволяет получить ощутимую экономию по времени. 

Пусть имеется два магазина. В магазине № 1 обслуживание осуществляется в порядке очереди, то есть здесь реализована дисциплина обслуживания FIFO (см. рис. 3.7.2).   

 

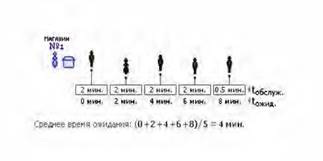
Рис. 3.7.2. Организация очереди по дисциплине FIFO

 

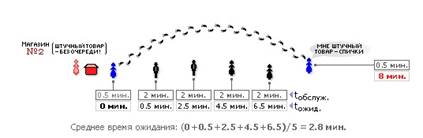
Рис. 3.7.3. Организация очереди по дисциплине SF

Время обслуживания t_{обслуж.} на рис. 3.7.2 показывает, сколько времени продавец затратит на обслуживание одного покупателя. Понятно, что при покупке штучного товара продавец затратит меньше времени на обслуживание, чем при покупке, к примеру, сыпучих продуктов, требующих дополнительных манипуляций (набрать, взвесить, высчитать цену и т. п). Время ожидания t_ожид. показывает, через какое время очередной покупатель будет обслужен продавцом. 

В магазине № 2 реализована дисциплина SF (см. рис. 3.7.3), означающая, что штучный товар можно купить вне очереди, так как время обслуживания t_{обслуж.} такой покупки невелико. 

Как видно из обоих рисунков, последний (пятый) покупатель собирается приобрести штучный товар, поэтому время его обслуживания невелико — 0,5 минут. Если этот покупатель придет в магазин № 1, он будет вынужден выстоять в очереди целых 8 минут, в то время как в магазине № 2 его обслужат сразу же, вне очереди. Таким образом, среднее время обслуживания каждого из покупателей в магазине с дисциплиной обслуживания FIFO составит 4 минуты, а в магазине с дисциплиной обслуживания КВ — лишь

2,8 минуты. А общественная польза, экономия времени составит: (1 – 2.8/4) × 100% = 30 процентов! В результате 30% сэкономленного для общества времени — и это лишь за счет правильного выбора дисциплины обслуживания. 

Специалист по системам должен хорошо понимать ресурсы производительности и эффективности проектируемых им систем, скрытые в оптимизации параметров, структур и дисциплинах обслуживания. Моделирование помогает выявить эти скрытые резервы. 

При анализе результатов моделирования важно также указать интересы и степень их выполнения. Различают интересы клиента и интересы владельца системы. Заметим, что эти интересы совпадают не всегда. 

Судить о результатах работы СМО можно по показателям.

Наиболее популярные из них: 

•       вероятность обслуживания клиента системой; 

•       пропускная способность системы; 

•       вероятность отказа клиенту в обслуживании; 

•       вероятность занятости каждого из канала и всех вместе; 

•       среднее время занятости каждого канала; 

•       вероятность занятости всех каналов; 

•       среднее количество занятых каналов; 

•       вероятность простоя каждого канала; 

•       вероятность простоя всей системы; 

•       среднее количество заявок, стоящих в очереди; 

•       среднее время ожидания заявки в очереди;   среднее время обслуживания заявки;   среднее время нахождения заявки в системе. 

Судить о качестве полученной системы нужно по совокупности значений показателей. При анализе результатов моделирования (показателей) важно также обращать внимание на интересы клиента и интересы владельца системы, то есть минимизировать или максимизировать надо тот или иной показатель, а также на степень их выполнения. Чаще всего интересы клиента и владельца между собой не совпадают или совпадают не всегда. Показатели обозначим H = {h₁, h₂, …}. 

Параметрами СМО могут быть: интенсивность потока заявок, интенсивность потока обслуживания, среднее время, в течение которого заявка готова ожидать обслуживания в очереди, количество каналов обслуживания, дисциплина обслуживания и так далее. Параметры влияют на показатели системы. Параметры обозначим как R = {r₁, r₂, …}. 

3.8.  Моделирование СМО в пространстве состояний 

Рассмотрим  следующую систему:

•       Требования поступают в случайные моменты времени, при этом промежуток времени Q между любыми двумя последовательными требованиями имеет показательный закон с параметром m, т. е. функция распределения: 

Fq(τ)=1-eμτ, τ≥0.                                (3.8.1)

•       Система обслуживания состоит из s одинаковых, пронумерованных приборов. 

•       Время t_обсл — случайная величина с равномерным законом распределения на отрезке [a, b]. 

•       Система без ожидания, то есть требование, заставшее все приборы занятыми, покидает систему. 

•       Дисциплина обслуживания такова: если в момент поступления k-го требования первый прибор свободен, то он приступает к обслуживанию требования; если этот прибор занят, а второй свободен, то требование обслуживается вторым прибором, и т. д. 

 Требуется оценить математические ожидания числа требований, обслуженных системой за время Т и получивших отказ.

 За начальный момент расчета выберем момент поступления первого требования Т₁ = 0. Введем следующие обозначения: Т_k — момент поступления k-го требования; t_i — момент окончания обслуживания требования i-м прибором, i = 1, 2, 3, ..., s.

Предположим, что в момент T₁ все приборы свободны.

Первое требование поступает на прибор 1. Время обслуживания этим прибором имеет равномерное распределение на отрезке [a, b]. Поэтому конкретное значение t_обсл этого времени находим по формуле: t_обсл. =a + r(b – a), где r — значение случайной величины R, равномерно распределенной на отрезке [0,1]. Прибор 1 будет занят в течение времени t_обсл. Поэтому момент времени t₁ окончания обслуживания требования прибором 1 следует считать равным: t₁ = Т₁+t_обсл. Затем следует добавить единицу в счетчик обслуженных требований и перейти к рассмотрению следующего требования.

Предположим, что k требований уже рассмотрено. Определим момент Т_k + 1 поступления (k + 1)-го требования. Для этого найдем значение t промежутка времени между последовательными требованиями. Так как этот промежуток имеет показательный закон, то: 

                                      (3.8.2)

где r-очередное значение случайной величины. Тогда момент

поступления (k + 1)-го требования: Т_k + 1 = Т_k + t.

Свободен ли в этот момент первый прибор? Для ответа на этот вопрос необходимо проверить условие t₁ ≤ T_k + 1. Если это условие выполнено, то к моменту Т_k + 1 первый прибор освободился и может обслуживать требование. В этом случае t₁ заменяем на (Т_k + 1 + t_обсл), добавляем единицу в счетчик обслуженных требований и переходим к следующему требованию. Если t₁ > Т_k + 1, то первый прибор в момент Т_k + 1 занят. В этом случае проверяем, свободен ли второй прибор. Если условие t₂ ≤ T_k + 1 выполнено, заменяем t₂ на (Т_k + 1 + t_обсл), добавляем единицу в счетчик обслуженных требований и переходим к следующему требованию. Если t₂ > Т_k + 1, то проверяем условие t₃ ≤ Т_k + 1 и т. д. Eсли при всех i от 1 до s имеет t_i > Т_k + 1, то в момент Т_k+ 1 все приборы заняты. В этом случае прибавляем единицу в счетчик отказов и переходим к рассмотрению следующего требования. Каждый раз, вычислив Т_k + 1, надо проверить еще условие окончания реализации: Т_k + 1 ≤ T. Если это условие выполнено, то одна реализация процесса функционирования системы воспроизведена и испытание заканчивается. В счетчике обслуженных требований и в счетчике отказов находятся числа n_обсл и n_отк.

Повторив такое испытание n раз (с использованием различных r) и усреднив результаты опытов, определим оценки математических ожиданий числа обслуженных требований и числа требований, получивших отказ:

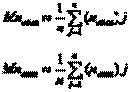                      (3.8.3)

                      (3.8.4)

где (n_обсл)j и (n_отк) j — значения величин n_обсл и n_отк в j-ом опыте.

Контрольные вопросы 

1.       Что называется статической и динамической моделями объекта?

2.       Какие типовые схемы используются при моделирования сложных систем и их элементов?