Статья на тему: "Формирование ФГ на урока в начальной школе"

Районный семинар учителей математики «Формирование функциональной грамотности на уроках математики и информатики»

Доклад учителя математики МБОУ Новоленинская СОШ

Шулуновой светланы Германовны

Формирование функциональной грамотности на уроках математики

Понятие «функциональная грамотность» впервые появилось в конце 60-х годов прошлого века в документах ЮНЕСКО и позднее вошло в обиход исследователей. Функциональная грамотность в наиболее широком определении выступает как способ социальной ориентации личности, интегрирующий связь образования (в первую очередь общего) с многоплановой человеческой деятельностью.

Одним из наиболее известных международных оценочных исследований, основанных на концепции функциональной грамотности, является Международная программа оценки учебных достижений 15-летних учащихся (ProgramforInternationalStudentAssessment - PISA), проводимой под эгидой Организации экономического сотрудничества и развития (ОЭСР). PISA оценивает способности 15-летних подростков использовать знания, умения и навыки, приобретенные в школе, для решения широкого диапазона жизненных задач в различных сферах человеческой деятельности, а также в межличностном общении и социальных отношениях.

В ходе тестирования в рамках PISA оцениваются три области функциональной грамотности: грамотность в чтении, математическая и естественнонаучная грамотность.

    В связи с этими требованиями, формирование  функциональной грамотности у учащихся становится очень важной целью для любого педагога. При изучении любого учебного предмета есть возможность для формирования и развития функциональной грамотности. В рамках  почти любой темы можно поставить   перед учащимся проблемы вне предметной области, которые решались бы с помощью знаний, полученных при изучении того или иного предмета. Математика предоставляет хорошие возможности для рассмотрения подобных задач. К сожалению, в учебниках математики предлагается большое количество технических упражнений, а задач практического содержания очень мало, а ведь практические задачи более сложные и трудоемкие. Конечно легче предложить ученику технические примеры по подстановке данных в формулу, но гораздо важнее научить ученика решать практические задачи.

Математическая грамотность – способность  проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем  в разнообразных контекстах реального мира.

 Разберем проблемы, которые возникают при формировании функциональной грамотности на уроках математики.

Во-первых, учащиеся  испытывают затруднения, связанные с избирательным  чтением. Они не  могут выделить существенную информацию, вопрос и данные, важные для решения задачи.  В своей работе я сталкивалась с тем, что ученик, видя нестандартную задачу, не приступал к решению, только из-за того, что его пугает большое количество данных или большой объём текстовой информации. Хотя со стандартными задачами  из учебника ученик справляется.  Невнимательность к прочтению условия, непривычность и необычность формулировок пугает обучающихся.  

Вторая  проблема при формировании математической функциональной грамотности: как сформулировать  (переформулировать) задачу, чтобы найти тот математический аппарат, с помощью которого уже можно решить привычную математическую задачу? Оценить математические связи между событиями. Это и есть основная проблема для школьника.  

Третья немало важная проблема возникает при  интерпретации результата, полученного математическими вычислениями, обратный перевод с математического языка на язык решаемой проблемной задачи. Очень часто учащиеся, получив ответ при решении задачи, не задумываются, возможен ли такой результат в реальности. И тогда мы можем получить в ответе: отрицательную строну  квадрата, отрицательную скорость движения  или не целое число строителей и т.п.  В таких ситуациях я привожу примеры: https://youtu.be/ICqPUwOGnxw - полтора землекопа

https://youtu.be/nUk6aKexLGY - сколько грибов в третьем бочёнке

Все задачи по развитию функциональной грамотности можно разбить на разделы:

• Прикидки и оценки
• Чтение текста
• Логическая грамотность
• Незнакомый контекст
• Работа с графическими представлениями информации
• Экономика

1.      Прикидки и оценки

Эти задания связаны с формированием чувства числа, пониманием порядка величин. Очень важно на практических задачах развивать чувство числа, что необходимо и при проверке ответа.

Задачи на прикидки и оценки встречаются и в ЕГЭ, и в ОГЭ, и в ВПР. Они включены в эти экзаменационные работы по причине того, что умение примерно оценивать значения величин необходимо человеку в повседневной жизни. Умение прикидывать часто не менее важно, чем умение получать точный ответ. Оно позволяет находить ошибки, принимать решения о покупке/не покупке, определять достоверность данных.

Задача 1. Показания счётчика электроэнергии 1 января составляли 32768 киловатт-часов, а 1 февраля — 32864 киловатт-часов. По текущему тарифу стоимость 1 киловатт-часа электроэнергии составляет 3 рубля 50 копеек. Сколько нужно заплатить за электроэнергию за январь?

Важно привить школьникам умение анализировать полученный в задаче ответ с точки зрения здравого смысла.(Базовая математика 11 класс)

Задача 2. Установите соответствие между величинами и их возможными значениями. К каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

Для её решения не нужно заучивать точные значения подобных величин. Достаточно привыкать к чувству порядка величины, изучая математику, физику, другие предметы.

Задача 3. На рисунке изображены автобус и автомобиль. Длина автомобиля равна 4,2 м. Какова примерная длина автобуса? Ответ дайте в сантиметрах.

В приведённой задаче верный ответ не единственный, можно указать любое значение, принадлежащее отрезку от 800 см до 1200 см.

Часто это сбивает ребят, они не понимают, как решать такую задачу. Необходимо подчеркнуть, что в задаче просят оценить именно примерную длину, искать точное значение не требуется. Также важно обратить внимание школьников на единицы измерения, в которых необходимо дать ответ: длина автомобиля дана в метрах, а ответ нужно указать в сантиметрах.

2. Чтение текста

Один из первых и самых ключевых навыков функциональной грамотности в математике — чтение сложных текстов, из которых не всегда очевидно, что именно требуется в задаче. К сожалению, этой теме уделяется мало внимания, особенно в старших классах. Статистика проведения ЕГЭ говорит о том, что даже в очень простых задачах школьники допускают обидные ошибки, неправильно читая условия задач и находя ответ не на тот вопрос, который предлагался в задаче. Например, в задаче на поиск меньшего корня квадратного уравнения школьники невнимательно читают условие и записывают в ответ значение большего корня. В 5-м и 6-м классах важно научить детей гибкому чтению на уроках математики.

Важным признаком того, что условие прочитано неверно, может служить очень сложное решение или «некрасивый» ответ в задаче.

 Задача-шутка, которая хорошо иллюстрирует, как важно внимательно читать условие.

Задача 4. Представьте, что вы капитан круизного лайнера, на котором путешествуют 500 пассажиров. Этот лайнер плывёт со скоростью 20 узлов в час (один узел равен 1,852 км/ч), предполагаемое время путешествия 7 дней. Сколько лет капитану корабля?

Все дети, когда им предлагаю эту задачу, сразу переходит к анализу чисел и пытаются выполнить какие-то вычисления, не обращая внимания на первую фразу. А именно она помогает ответить на вопрос задачи: решающему достаточно указать свой возраст.

Задача 5. Братья Андрей и Миша Ивановы играют в игру. Андрей загадывает число n, имеющее ровно 7 простых делителей. Миша придумывает гладкое пятимерное многообразие, описываемое формулой степени не более чем n². Андрей указывает 5 точек на этом многообразии и объявляет длины не более чем 7 отрезков, соединяющих эти точки в пространстве R25. Если выбранные точки вместе с указанными Андреем отрезками образуют жёсткую структуру второго порядка, то побеждает Миша. В противном случае мальчики меняются местами: Андрей придумывает другое гладкое многообразие, проходящее через эти 5 точек, и Миша указывает 5 точек на нём. Игра продолжается, пока либо у кого-то из мальчиков не получилась жёсткая структура, либо не прошло 1003 хода — в этом случае побеждает Миша. В зависимости от n назовите фамилию победителя при правильной игре.

Чтобы дать верный ответ на задачу, достаточно прочитать только первое и последнее предложения из условия.

3.Логическая грамотность

Школьникам, которые никогда не будут использовать математику в работе, всё равно придётся принимать в жизни решения, которые будут основаны на анализе сложившейся ситуации, на анализе входных данных. Эти данные могут быть текстом договора, надписью на информационном щите, инструкцией к электроприбору и так далее.

В ОГЭ, ЕГЭ и PISA есть задачи такого характера. Вот задача из открытых источников PISA.

Задача 6. Люди, проживающие в многоквартирном доме, решили выкупить этот дом. Они вместе хотят собрать деньги таким образом, чтобы каждый из них заплатил сумму, пропорциональную площади его квартиры. Например, мужчина, проживающий в квартире, которая занимает 1/5 площади всех квартир, должен будет заплатить 1/5 от всей стоимости здания. Выберите все верные утверждения.

A. Человек, проживающий в самой большой квартире, заплатит больше денег за каждый квадратный метр своей квартиры, чем человек из самой маленькой квартиры.

B. Зная площадь двух квартир и цену одной из них, мы можем вычислить цену второй.

C. Зная цену здания и сумму, которую заплатит каждый владелец, мы можем вычислить общую площадь всех квартир.

D. Если бы общая стоимость здания была снижена на 10%, каждый из владельцев заплатил бы на 10% меньше.

В этой задаче верны утверждения B и D, а утверждения A и C неверны.

Задача 7. Прочитайте текст и ответьте на вопросы 1–2.

Домохозяйке Наталье Анатольевне для приготовления обеда необходимо купить следующий набор продуктов: 1 баночку кукурузы Bonduelle, 2 упаковки крабовых палочек Vici, 10 яиц, 1 литр молока «Простоквашино» и хлеб. Рядом с домом Натальи Анатольевны располагаются сетевые магазины «Магнит», «Монетка» и «Пятёрочка». У Натальи Анатольевны в телефоне установлено приложение  и она постоянно следит за обновлениями акционных товаров в этих магазинах. Цены на необходимые товары в данных магазинах представлены в таблице.

Вопрос 1/2. Определите стоимость необходимого набора товаров, если Наталья Анатольевна будет покупать отдельные продукты в тех магазинах, где наиболее выгодно.

Запишите ответ и приведите соответствующее решение.

Вопрос 2/2. Во сколько рублей обойдётся покупка Наталье Анатольевне, если она будет покупать все продукты в ближайшем к её дому магазине «Пятёрочка» и на кассе предъявит свою дисконтную карту, предоставляющую ей скидку 5% на весь ассортимент? Ответ округлите до целых.

Запишите ответ и приведите соответствующее решение.

Задача 8. «ПОДГОТОВКА К ШКОЛЕ»

Прочитайте текст и ответьте на вопросы 1–3.

Цены на товары

Вопрос 1/3. Определите стоимость необходимого набора товаров без учёта скидки.

Запишите ответ и приведите соответствующее решение.

Вопрос 2/3. Определите стоимость необходимого набора товаров с учётом действующих в этом магазине в этот день скидок.

Запишите ответ и приведите соответствующее решение.

Вопрос 3/3. Определите сколько денег сэкономили Ваня с мамой, приобретая товары в магазине «Народный».

Запишите ответ и приведите соответствующее решение.

4.      Незнакомый контекст.

Задачи, которые требуют применения математических методов, окружают нас повсюду, в том числе в новых для нас ситуациях. Многие области знания, в том числе гуманитарные, используют математические модели. Поэтому человеку, работающему в любой области, придётся их анализировать.

Задачи с незнакомым контекстом занимают значительное место в международных исследованиях качества образования, в том числе в исследовании PISA. В таких задачах описана незнакомая для человека ситуация, в которой ему необходимо применить зачастую совсем несложные математические методы. Такие задачи присутствуют и в ЕГЭ, и в экзамене за 9 класс.

1. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I=, где ε — ЭДС источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 4% от силы тока короткого замыкания Iкз=? (Ответ выразите в омах.)

При решении таких задач учащиеся начинают применять знания физики, хотя этого для получения ответа не требуется, а только лишь усложнит задачу.

2. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 185 МГц. Скорость погружения батискафа v (в м/с) вычисляется по формуле v=c⋅, где c=1500 м/c — скорость звука в воде, f₀ — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц.

Эту задачу можно упростить, если мысленно отбросить подробности сюжета и вычленить математическую модель.

[...] испускает [...] импульсы частотой 185 МГц. Скорость погружения [...] v (в м/с) вычисляется по формуле v=c⋅, где c=1500 м/c — скорость звука в воде, f₀ — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц.

После такой процедуры становится понятно, что все значения переменных известны, кроме одного, и его уже несложно найти подстановкой в формулу.

5.      Работа с графическим представлением информации.

Графическое представление информации бывает в виде графиков, схем, диаграмм и таблиц.

-На схеме зала кинотеатра отмечены разной штриховкой места с различной стоимостью билетов, а черным закрашены забронированные места на некоторый сеанс.

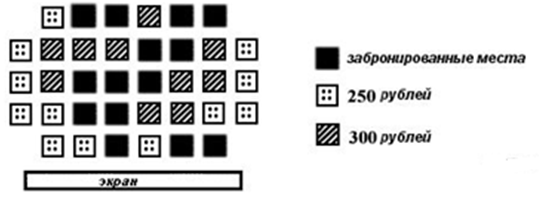
Сколько рублей заплатят за 5 билетов на этот сеанс пятеро друзей, если они хотят сидеть на одном ряду и выбирают самый дешевый вариант?

В ответе укажите номер правильного варианта.

1) 1300

2) 1250

3) 1350

            4) 1500

Заключение.

В своей работе я показала только часть задач, используемых для формирования функциональной грамотности. Все они обеспечивают личное саморазвитие, самостоятельность в приобретении знаний, формируют коммуникативные навыки, умение использовать информацию, предприимчивость и креативность.

Однако, существуют проблемы, которые мешают развитию математической грамотности:

1)      Низкий уровень вычислительных навыков.

2)      Отсутствие практической направленности в математике (дефицит практико-ориентированных задач в учебниках)

3)      Натаскивание на решение по аналогии, неумение организовать свою учебную работу дома, ответственность за выполнение домашних заданий.

4)      Непонимание учащимися необходимости заучивания теоретических понятий (правил, формул, теорем).

Использование практико-ориентированных и ситуационных задач в учебном процессе позволяет хотя бы частично эти проблемы решить. Хоть эти задачи и не связаны с непосредственным повседневным опытом обучающегося, но они помогают им увидеть и понять, как и где могут быть полезны в будущем знания из различных предметных областей.

Скачано с www.znanio.ru