ФОРМИРОВАНИЕ ЭВРИСТИЧЕСКИХ УМЕНИЙ УЧАЩИХСЯ 

ПРИ ИЗУЧЕНИИ ТЕМЫ «ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ»

В настоящее время в образовательном процессе большое внимание уделяется развитию универсальных учебных действий, которыми должны овладеть обучающиеся при освоении учебного материала. В частности, при изучении курса алгебры и начал математического анализа, так как данная дисциплина является основополагающей и фундаментальной для развития личности обучающихся, их умения самостоятельно обрабатывать и анализировать новую информацию, использовать знания в новых нестандартных ситуациях, осваивать новые формы деятельности, способности и готовности к самостоятельному решению учебных задач и творческой деятельности.

Под универсальными учебными действиями в широком смысле

А.Г. Асмолов [1, с.27], понимает, умения учиться, т.е. способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта, а в узком смысле – совокупность способов действий, обеспечивающих самостоятельное усвоение новых знаний, формирование умений, которые включают в себя организацию этого процесса.

На наш взгляд, наиболее эффективной подходом, направленным на овладение обучающимися универсальными учебными действиями, является организация учебно-познавательной эвристической деятельности учащихся.

Под учебно-познавательной эвристической деятельностью, будем понимать деятельность обучающихся, организованную и управляемую учителем с использованием разнообразных эвристических приемов, методов и средств, направленную на создание новой системы действий по поиску неизвестных ранее закономерностей, на формирование процессов, обеспечивающих познавательную и творческую деятельности, в результате которой учащиеся активно овладевают знаниями, развивают эвристические умения и личностные качества [3, с.214].

Управление эвристической деятельностью обучающихся в процессе обучения математике исследовали Н.П. Алешина, Е.В. Власенко, И.В. Гончарова, И.А. Горчакова, Т.С. Жукова, Л. Ларсон, П. Лилжедахл, С.Р. Мугаллимова, О.К. Огурцова, Дж. Пойа, В.С. Прач, К. Робинсон,

Н.Ю. Ротанёва, Г.И. Саранцев, Е.И. Скафа, И.Л. Тимофеева и др.

Главной целью организации учебно-познавательной эвристической деятельности в курсе алгебры и начал математического анализа, является формирование эвристических умений обучающихся. Эвристические умения – это умения осуществлять целенаправленный поиск решения нестандартной задачи путем использования эвристических приемов [3, с.215]. Применение эвристических умений на практике – это процесс осмысленного осуществления учащимися целенаправленного поиска решения определённой проблемы (в частности математической задачи) с помощью эвристических приемов, для которого характерными являются самостоятельность обучающихся и наличие в учебной элементов творческой деятельности, направленных на познание окружающей действительности [2, с.44].

Предпосылкой формирования эвристических умений обучающихся, является использования, в процессе обучения курсу алгебры и начал математического анализа различных эвристических приемов.

Под эвристическими приемами, Е.И. Скафа, понимает особые приемы, составляющие поисковые стратегии и тактики, определяющие самое общее направление мысли, сформированные в ходе решения одних задач и более или менее сознательно переносящиеся на другие [3, с.215].

В процессе формирования эвристических умений обучающихся, в курсе алгебры и начал математического анализа наиболее эффективным является использование эвристических задач как нестандартных задач, в процессе поиска решения которых обучающийся попадает в ситуацию проявления своих эвристических позиций [3, с.215].

Рассмотрим систему задач, с помощью которой можно формировать эвристические умения обучающихся, при изучении темы: «элементы теории вероятностей» в курсе алгебры и начал математического анализа, на этапе закрепления изученного материала. Данные задачи предусматривают формирование у обучающихся таких эвристических умений как, выделять подзадачи, разбивать «целое на части» и реконструировать «целое по его частям».

Задача 1. В урне 10 белых и 15 черных шаров, которые тщательно перемешены. Наудачу из урны извлекают 3 шара, какая вероятность того, что извлечены только 2 черных шара?

Эвристическая подсказка: используйте эвристические приемы:

выделение подзадач, разбиение «целого на части», реконструкция целого «по части».

Решение. Разбиваем данную задачу на части и выделяем следующие подзадачи.

Первая подзадача. Сколькими способами можно выбрать 3 шара из урны, в которой 10 белых и 15 черных шаров, которые тщательно перемешены?

Так как порядок шаров роли не играет, то используем сочетания.

Количество всех возможных вариантов равно: 

Вторая подзадача. Сколькими способами можно выбрать 2 черных шара и 1 белый шар из урны, в которой 10 белых и 15 черных шаров, которые тщательно перемешены?

Разбиваем данную подзадачу «на части»: два черных шара можно взять лишь из 15 черных шаров, количество таких способов  .

А 1 белый шар можно взять лишь из 10 белых шаров, количество таких способов ^C₁₀¹ .

Реконструируем «целое по части» и определяем количество способов, которыми можно выбрать 2 черных шара и 1 белый шар из урны, в которой 10 белых и 15 черных шаров.

Так как нужно выбрать 2 черных шара и 1 белый шар из урны, то используем правило произведения, имеем:

Третья подзадача. Определить вероятность извлечения 2 черных шаров и 1 белого шара, из урны в которой 15 черных шаров и 10 белых.

Для определения вероятности, находим соотношение, способов которыми можно извлечь из урны, в которой 15 черных шаров и 10 белых, 2 черных шара и 1 белый шар, к числу способов, которыми можно извлечь 3 шара из урны, в которой 25 шаров.

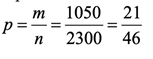
Ответ: p = .

Задача 2. Достаточным условием сдачи экзамена является ответ на один из двух вопросов билета, предлагаемого преподавателем студенту. Количество различных вопросов, из которых составляются билеты равно 50. Студент не знает ответов на 8 из них. Какова вероятность сдачи студентом экзамена?

Эвристическая подсказка: используйте эвристические приемы:

рассмотрение частных случаев, разбиение «целого на части», выделение подзадач и реконструкция целого «по частям».

Решение. Рассматриваем два частных случая. Студент успешно сдаст экзамен, если он знает ответ либо на один вопрос из билета, либо на два. Разбиваем данную «задачу на части».

Первый частный случай: студент знает ответ на один вопрос из билета. Выделяем подзадачи.

Первая подзадача. Сколькими способами можно выбрать 2 вопроса из 50?

Вторая подзадача. Сколькими способами можно выбрать 1 вопрос из 42, и 1 вопрос из 8?

m  = 42 8 = 336

Третья подзадача. Найти вероятность того, что студент знает ответ ровно на один вопрос из билета.

Второй частный случай: студент знает ответ на два вопрос из билета. Выделяем подзадачи.

Первая подзадача. Сколькими способами можно выбрать 2 вопроса из 50?

Вторая подзадача. Сколькими способами можно выбрать 2 вопроса из 42.

Третья подзадача. Найти вероятность того, что студент знает ответ на два вопрос из билета.

Реконструируем целое «по частям» и находим вероятность успешной сдачи студентом экзамена. Имеем 

Ответ: p≈ 0,9771.

Формирование эвристических умений обучающихся, в процессе изучения курса алгебры и начал математического анализа, будет способствовать овладению ими универсальными учебными действиями. И как результат позволит обучающимся более глубоко и осознанно изучать учебный материал, расширит их творческо-поисковый потенциал, даст возможность переносить знания и действия в нестандартные ситуации или создавать новый способ действий.

Литература

1.                 Асмолов А.Г. Как проектировать универсальные учебные действия в начальной школе: от действия к мысли: пособие для учителя / А.Г. Асмолов, Г.В. Бурменская, И.А. Володарская, И.А. Карабагова, Н.Г. Салмина, С.В. Молчанов // под ред. А.Г. Асмолова – Москва: Вентана – Граф Просвещение, 2014. – 152 с.

2.                 Скафа Е.И. Технологии эвристического обучения математике:

учебное пособие. 2-е изд испр. и доп. / Е.И.Скафа, И.В.Гончарова, Ю.В.Абраменкова. – Донецк: ДонНУ,