Свойства S-преобразований.docx

Свойства S-преобразований.

Имеется множество n-разрядных двоичных слов. S-преобразование есть отображение этого множества на самое себя. Отображение (S-преобразование) можно задавать либо правилами, либо таблично. Например, для 2-х разрядных слов:

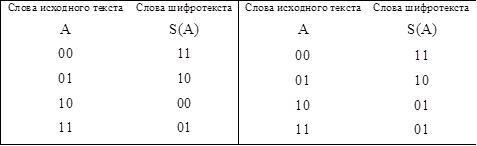сингулярный блок

Всего во множестве имеется 2n n -разрядных слов, а различных отображений в

этом множестве2(

n )2(ⁿ ) .

Однако, все отображения, содержащие сингулярные множества, нежелательны, т.к. приводят к неоднозначности дешифрования шифротекста. Поэтому применяют только обратимые (несингулярные) S-преобразования. Количество таких S-преобразований равно 2(n )!.  Фактически  —  это  перестановки  слов  в  таблице  обратимого  S-преобразования, которое называют аффинным преобразованием.

Аффинным    называют    преобразование     S,     обладающее     свойством:    если      A      и      B      два      двоичных      вектора,      одинаковой       размерности;  если    S    есть    преобразование    пространства    этих    векторов    в     себя,     и     если Z, вычисляемое как:

=     A Å B Å S ( A) Å S (B)

оказывается постоянным для всех A и всех B, то S является аффинным преобразованием.

Проверим     аффинность     для     приведённой     выше     таблицы     обратимого преобразования.

A=00          A=00                            A=01   …

B=00          B=01                            B=11   …и т.д. для всех пар

Å                   00               01                                 10   …

ASÅ B

S(00)=11    S(01)=10                       S(10)=00

по     S(A)=11      S(А)=11                        S(A)=10

таблице     S(B)=11      S(B)=10                        S(B)=01

Z=11           Z=11       и т.д              Z=11   и т.д. Z=const