Технологическая карта урока "Физический смысл производной"

Тема урока

Физический смысл производной  (интегрированный урок математики и физики)

Тип урока

урок «открытия» нового знания ( 2 урока-1ч 20 мин)

Цель урока

Задачи урока

  формирование умений  применять методы дифференциального исчисления для решения прикладных физических задач

1. Изучить физический смысл производной как скорости изменения функции;
2. Использовать приобретенные знания и умения в практической деятельности и для решения прикладных физических задач на ЕГЭ;
3. Формировать у учащихся умение выделять главное, существенное в изучаемом материале, сравнивать, обобщать изучаемые факты, логически излагать свои мысли; формировать навыки взаимоконтроля.

Планируемый результат обучения

В результате изучения темы обучающиеся должны

знать:

- понятие физического смысла производной;

- алгоритм решения задач с использованием данного понятия

уметь:

 -   уметь использовать приобретённые знания при решении различного вида учебных и прикладных задач;

-  планировать свои действия в соответствии с поставленной задачей;

-  формировать навыки объективной самооценки и взаимооценки;

- работать в  группе  (планировать работу, распределять   её между членами   группы, совместно оценивать  результат работы, слушать собеседника и вести   диалог)

Ресурсы

Учебник  Ю.М.Колягин и др., Алгебра и начала математического анализа,11 класс, Просвещение, 2020

-Презентация к уроку.

 -  Мультимедийный проектор.

 -  Раздаточный материал.

 - Лист самооценки и взаимооценки.

Методы и формы обучения

Работа с книгой, текстом, обсуждение, проблемное обучение, обучающий контроль;

групповая, индивидуальная, фронтальная

Основные понятия

    Производная, правила и формулы дифференцирования,  геометрический и  физический смысл производной, скорость, ускорение, сила, материальная точка, равноускоренное движение, графики функций

Планируемые результаты

Предметные

Метапредметные УУД

Личностные УУД

-решение  прикладных физических задач с использованием физического смысла производной,

 - умение,  используя алгоритм, комментировать свои действия, используя математические термины

- применение знаний в различных ситуациях

Регулятивные:

 - понимание учебной задачи урока; определение цели учебного задания;

  - контроль своих действий в процессе выполнения заданий;

  - обнаружение и исправление ошибок; 

   - оценивание своих достижений.

Познавательные

: - применение алгоритма решения квадратных уравнений с параметром24.2 при решении практических задач;

- овладение умением видеть проблему и желанием ее решить

Коммуникативные:

-  представление результата деятельности;

-   умение вести диалог с оппонентом;

-  умение пользоваться речью для объяснения действий

формирование внутренней позиции учащегося;       активной мотивации учебной деятельности, самооценки;    необходимости приобретения новых знаний.

ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА

Этапы урока

Время (мин.)

Деятельность учителя

Деятельность учащихся

Формы организации совзаимодей-ствия на уроке

Универсальные учебные действия (УУД)

Формы контроля

1

Здравствуйте, ребята,   начинаем наш урок, чтобы он вам запомнился

 важно  с каким настроением вы будете приобретать новые знания. Для мотивации учебной деятельности перед началом каждого этапа урока, мы будем вас настраивать на учебную работу известными пословицами и поговорками.

Мотивация к учебной деятельности и целеполагание

3

Дети организуют свое рабочее место, проверяют готовность к уроку.

Эмоциональный настрой

Фронтальная,      групповая

Регулятивные УУД:

формирование способности к организации своей деятельности

Личностные УУД:

осмысление внутренней позиции ученика на уровне положительного отношения к уроку

Коммуникативные

УУД:

оформление своих мыслей согласно заданным рамкам обсуждения, аргументация своих суждений

Актуализация знаний, постановка проблемной ситуации

9

3

15

1) Повторение учебного материала

  а) программированный контроль

 « Лиха беда начало»

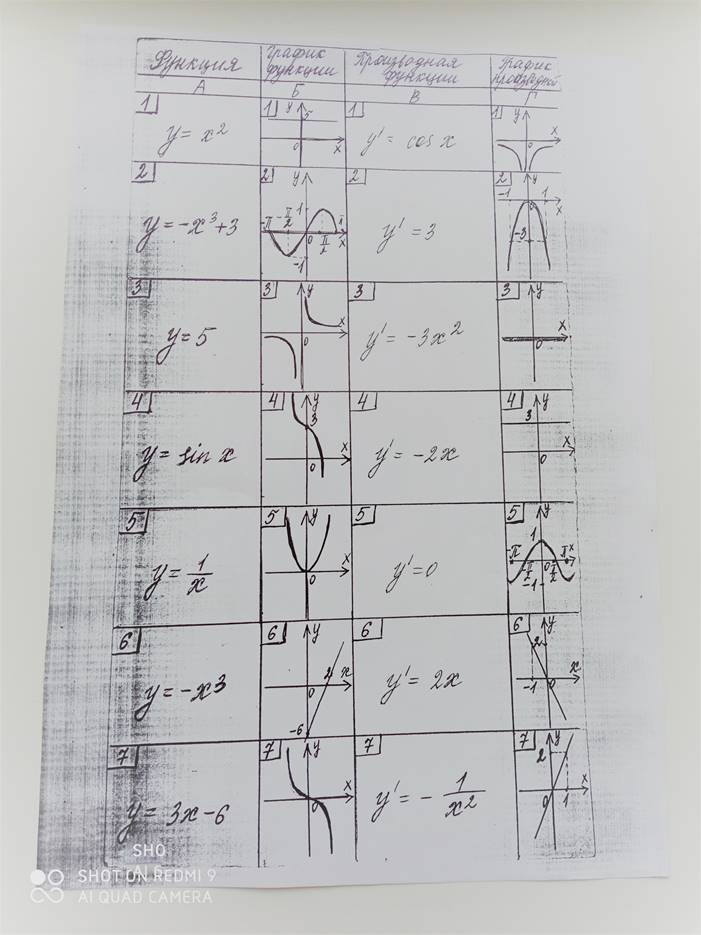
Вам необходимо поставить в соответствие заданной функции ее график, производную, график производной. Результат записать в тетради по форме  1-4-2-7 ( см. приложение )

б)   формулы

«Повторенье-мать ученья»

Повторяем правила и формулы дифференцирования, формулы, характеризующие равноускоренное движение, колебания

в) мозговой штурм

« Взялся за гуж, не говори, что не дюж»

Ребята, мы вам предлагаем примеры, которые вы решаете, затем заполняете ячейку таблицы на карточке, под числом-соответствующая буква. Решив их, вы узнаете имя и фамилию известного французского математика, доказавшего теоремы, которыми мы пользуемся при вычислении производной

Огюстен Луи Коши ( 1789-1857) ( демонстрируется портрет ученого) –крупный французский математик. Доказал ряд замечательных теорем в области математического анализа. Работы Коши относятся к различным областям математики и математической физики.

2) Постановка учебной задачи.

Ребята, решите задачу.

 Две материальные точки движутся прямолинейно по законам

S₁(t)=2,5t²-6t+1 и S₂(t)=0,5t² +2t-3. В какой момент времени t₀ скорости их равны, т.е. v₁(t₀)=v₂(t₀)?  

Какая была тема нашего прошлого урока?

Раз уж мы  заговорили о физике, задаем вам вопрос, а только ли геометрический смысл имеет производная, как вы думаете, какой смысл может еще иметь производная?

Как вы считаете, какой  будет тема нашего урока?

Тема фиксируется на доске и в тетрадях учащихся.

Ребята, какую цель поставим перед собой на данном уроке?

Определим задачи на урок.

 В чем же заключается физический смысл производной?

 Учащиеся выполняют работу, проверяют результаты работы в форме взаимоконтроля

 Оценка «5»-7 номеров, «4»-5-6 номеров, «3»-4 номера, «2»-менее 4

 .

Фронтальный опрос учащихся

  Ребята выполняют задания по вариантам.

( 1 вариант №№1-6, 2 вариант №№7-12)

Если задания выполнены правильно, то получим

Огюстен Луи Коши, слушают краткую информацию о нем

Учащиеся предлагают различные варианты решения, говорят о трудностях, которые у них возникли

Геометрический смысл производной

Физический, механический

Физический смысл производной

Вместе с учителем     формулируют цель и  определяют задачи урока

Фронтальная, индивидуальная, групповая

Личностные:

самоопределение; нравственно-этическое оценивание усваиваемого содержания; осознание ответственности за общее дело;

Познавательные: анализ, синтез, сравнение, обобщение, аналогия, извлечение необходимой информации; постановка и формулирование проблемы; структурирование знаний; осознанное и произвольное построение речевого высказывания; моделирование и преобразование моделей разных типов; установление причинно-следственных связей; самостоятельное создание способов решения проблем творческого и поискового характера на основе метода рефлексивной самоорганизации; построение логической цепи рассуждений.

Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно; планирование;

Коммуникативные: выражение своих мыслей с достаточной полнотой и точностью; учёт разных мнений, координирование в сотрудничестве разных позиций; планирование учебного сотрудничества с учителем и сверстниками.

Текущий контроль, устный опрос

 Совместное «открытие» новых знаний

15

  « Знание- дело наживное»

Среди предположений о решении проблемной задачи о нахождении скоростей в момент времени t₀, было и нахождение производной S'(t).

Давайте решим эту задачу, используя предположение.

Ребята, откройте стр.66 учебника и поработайте с текстом

Давайте рассмотрим связи некоторых физических величин с понятием производной

1. При равномерном прямолинейном движении v=,a=0 при неравномерном v=s'(t), a=v'(t)=s"(t)
2. При постоянном токе I=, при переменном токе I=q'(t). При  равномерном движении по окружности =, при неравномерном-='(t)
3. Рассмотрим известную формулу Q=cmΔt, где Q-количество теплоты, m-масса, Δt-разность температур, с-удельная теплоемкость. Для m=1 кг, Q=cΔt

Для изменяющейся температуры с=Q'(t)

 .

 Учащиеся решают задачу, проверяют решение

Работают с учебником, рассматривают понятие мгновенной скорости, убеждаются в том, что s'(t)=v(t)

Изучают понятие второй производной и выясняют, что

a(t)=v'(t)=s"(t)

Групповая,

парная,

фронтальная

Текущий контроль, самоконтроль, взаимоконтроль

Динамическая пауза

2

Музыкальная

физкультминутка

                ( релаксирующая музыка)

« В здоровом теле здоровый дух»

Личностные УУД:

умение применять правила охраны своего здоровья

Первичное закрепление с проговариванием во внешней речи

23

 « Корень учения горек, да плод его сладок»

А теперь мы с вами научимся применять  полученные знания при решении прикладных физических задач 

1. Работа с учебником

№№26(2), 27(2), 28 (2)

2.  Тест по КИМам ЕГЭ

« Терпение и труд все перетрут»

     Часть А

К каждому заданию части А дано несколько ответов, из которых только один верный. Решите задание, выберите верный на ваш взгляд ответ

1.В чем сущность физического смысла производной?

А.Скорость

Б.Ускорение

В.Угловой коэффициент

Г.Перемещение

2.Точка движется по закону s(t)=2t³-3t. Чему равна скорость в момент t₀=1 c?

А. 15

Б. 12

В. 9

Г. 3

3.Зависимость пути от времени движения выражается формулой s(t)=. Назовите формулу ускорения

А.

Б. 2gt

В. gt

Г.g

4. Тело движется прямолинейно по закону s(t)=-2t²+3t+1. В какие моменты времени t ее скорость будет равна нулю?

А. 1и3

Б.1и4

В.2

Г.2и0

5. Скорость тела, движущегося прямолинейно, определяется по формуле v(t)=5t³+t². Чему равно ускорение тела в момент времени t₀=1c?

А. 17

Б. 32

В. 30

Г. 16

              Часть В

1. Точка движется по координатной прямой согласно закону x(t)=10+8t-0,5t², где x(t)-координата точки в момент времени t. Найдите ее скорость при t=6.
2. Маховик, задерживаемый тормозом, поворачивается за t с на угол 3t-0,1t²(рад). Найдите: а) угловую скорость вращения маховика в момент времени t=7c;

б) в какой момент времени маховик остановился?

    3.   Найдите силу F, действующую на              материальную точку с массой m=2 кг, движущуюся прямолинейно по закону x(t)= 2t³-t² при t=2с.

Критерии оценивания:

«3»-за правильное решение 4-5 заданий части А;

«4»-за правильное решение части А и 1 или 2 задания части В;

«5»-за правильное решение части А и части В

Работа у доски

Учащиеся выполняют задания в группах разноуровнего состава, старший группы распределяет задания между членами группы, осуществляется взаимопроверка, далее старший каждой группы проверяет ответы по ключу, проговаривает какие трудности возникли при решении теста, совместно с учителями осуществляет разбор заданий с неправильным ответом.

Фронтальная,

индивидуальная

Регулятивные:

 овладение приёмами самоконтроля, сличения способов действий и его результата с заданным эталоном

Познавательные:

- уметь находить ответы на вопросы 

- уметь преобразовывать информацию           из одной формы в другую (составлять ответы на вопросы);

- уметь осуществлять анализ объектов с выделением существенных и несущественных признаков;

 - уметь осуществлять поиск необходимой информации для выполнения учебного задания с использованием учебной литературы.

Коммуникативные:

- уметь участвовать в учебном диалоге при обсуждении изученного;

- уметь учитывать разные мнения и интересы и обосновывать собственную позицию;

-  уметь договариваться и приходить к общему решению в совместной деятельности;

 уметь осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь

Текущий контроль

Самостоятельное применение знаний

6

Примените свои знания при выполнении тестовой  работы на установление соответствия.     

 « Чему смолоду не научился, того и под старость не будешь знать»

Тест « Берегись автомобиля» ( нестандартная ситуация)

Милиционер Подберезовиков преследует Деточкина, который угнал автомобиль. Преследователь и преследуемый движутся по прямолинейному шоссе, но движение их происходит по разным законам.

Деточкин едет по закону x=f(t), а Подберезовиков- по закону x=g(t). В пути они попадают в трудные ситуации, о чем мы узнаем по их поведению

Проверяют своё умение применять алгоритм     в типовых условиях, выполняют тест на установление соответствия между предложением , отражающем физическое явление и соответствующими символическими записями, итоговая оценка записывается в листе самооценки и взаимооценки.

Групповая, 

индивидуальная

Познавательные:

 выбор информации.

Регулятивные:

планирование  действий для выполнения самостоятельного задания;

Коммуникативные:

умение выражать свои мысли, вести доказательные объяснения.

Самостоятельная работа

Итог урока. Рефлексия

2

« Что посеешь, то и пожнешь»

- Как вы думаете, справились ли  вы с поставленными в начале урока задачами?

 Кто доволен результатом урока?

Кому помогала справляться с заданиями вера в себя?

Кто уходит после урока с хорошим настроением?

Учащиеся анализируют свою работу и работу групп, фронтально отвечают на вопросы.

Коммуникативные: умение строить высказывание с учётом норм языка.

Личностные: личностное самоопределение.

Регулятивные:

умение адекватно оценивать свою деятельность и деятельность своих товарищей

Домашнее задание

2

« Тяжело в ученье-легко в бою»

 1.  №№ 28(2),59,60

2.Творческое задание.

   Составить  3 прикладных физических задачи и решить их.