Технология развития критического мышления

Лабораторная работа №8

«Современные педагогические технологии

в преподавании информатики»

Технология развития критического мышления

Цель работы: изучить теоретические основы применения технологии развития критического мышления, описать этапы реализации технологии развития критического мышления при изучении курса информатики.

Задание 1 (4 балла). Описать этапы реализации технологии развития критического мышления при изучении одной из тем школьного курса информатики (задание выполняется по вариантам).

Вариант 1. Правило перевода целых десятичных чисел в систему счисления с основанием q

Вариант 2. Двоичная система счисления. Двоичная арифметика

Вариант 3. Свойства логических операций.

Вариант 4. Высказывание. Логические операции.

Вариант 5. Файлы и файловые структуры.

Вариант 6. Системы программирования и прикладное программное обеспечение.

Вариант 7. Информационные процессы. Хранение и передача информации.

Вариант 8. Табличные модели

Вариант 9. Способы записи алгоритмов

Вариант 10. Алгоритмическая конструкция «ветвление». Полная форма ветвления.

Пример реализации

технологии развития критического мышления

при изучении темы «Графические модели»

При изучении темы «Графические модели» школьники уже знакомы с понятиями модель, моделирование, информационная модель.

Цель выполнения заданий: познакомить с различными графическими моделями и областями их применения.

Стадия «Вызов»

С обучающимися проводится беседа, в ходе которой строится кластер основных понятий.

Вопрос. На протяжении нескольких уроков изучалась тема моделирование. Как выдумаете, какое понятие в этой теме можно назвать ключевым?

Ответ. Ключевым понятием темы является понятие «модель».

Вопрос. На какие виды можно разделить множество моделей?

Ответ. Модели можно разделить на материальные (натурные) и информационные модели.

Вопрос. Какие виды информационных моделей вы знаете?

Ответ. Информационные модели бывают знаковыми, табличными, графическими.

Полученный кластер

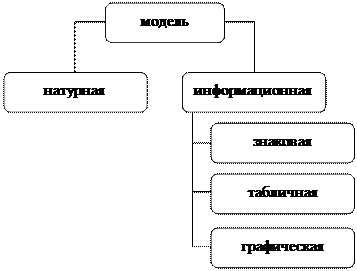
Вопрос. Как вы думаете, для чего нужны графические модели?

Ответ. Графические модели нужны для наглядного представления информации.

Вопрос. Какие примеры графических моделей вы можете привести?

Ответ. К графическим моделям относятся: карта, чертеж, план.

Вопрос. Какие еще примеры графических моделей вы знаете?

Школьники затрудняются с приведением примеров, и им предлагается изучить материал по теме «Графические информационные модели» (см. Приложение 1).

Стадия «Осмысление»

Изучение нового материала осуществляется с помощью приема Инсерт (insert).

При чтении текста Приложения 1 учащиеся на полях расставляют пометки. Пометки должны быть следующие:

v если то, что вы читаете, соответствует тому, что вы знаете;

– если то, что вы читаете, противоречит тому, что вы уже знали, или думали, что знали;

+ если то, что вы читаете, является для вас новым;

? если то, что вы читаете, непонятно, или же вы хотели бы получить более подробные сведения по данному вопросу.

Стадия «Рефлексия»

На стадии рефлексии происходит заполнение таблицы Инсерт

Учитель с обучающимися обсуждает заполненную таблицу, разъясняет материал, который вызвал вопросы.

Пример блок-схемы перехода улица по светофору

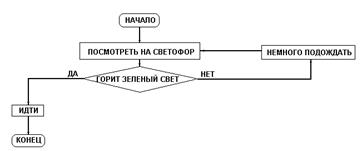
Пример ориентированного графа, который указывает направление движения между населенными пунктами А, Б, В, Г, Д, Ж, Е

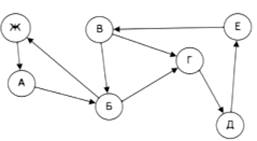
Пример изоморфных графов

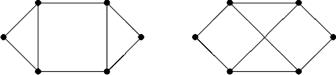
Пример связных графов

После разъяснения непонятных моментов школьники отвечают на вопросы учителя.

1.     Какие информационные модели относят к графическим?

2.     Приведите примеры графических информационных моделей, с которыми вы имеете дело:

a.      при изучении других предметов;

b.     в повседневной жизни.

3.     Что такое граф? Что является вершинами и рёбрами графа? Укажите на собственном графе-примере.

4.     Какой граф называют ориентированным?

5.     Какие графы называют изоморфными?

6.     Что такое дерево?

Задание 1 (8 баллов). Составить технологическую карту урока по одной из тем школьного курса информатики (на Ваш выбор). При проведении урока используется технология развития критического мышления.

Структура технологической карты урока информатики

Информационный блок

Тема урока:___________________________________________________________________

Цели урока:

·      обучающая: _________________________________________________________;

·      развивающая: _______________________________________________________;

·      воспитывающая: _____________________________________________________;

Результаты урока: ____________________________________________________________

Оборудование, необходимое для проведения урока: __________________________________
_____________________________________________________________________________

Программное обеспечение, необходимое для проведения урока:________________________

План урока

1. 1 Этап                                время, отводимое на данный этап урока

2. 2 Этап                                время, отводимое на данный этап урока

……..

Содержательно-деятельностный блок

Ход урока

Контрольные вопросы

1.      Что понимается под технологией развития критического мышления?

2.      Какие существуют приемы реализации технологии развития критического мышления?

Приложение 1

Графические информационные модели

Графическая информационная модель – это наглядный способ представления объектов и процессов в виде графических изображений. К ним относятся: чертежи, графики, диаграммы, образные модели, схемы (карты, графы, блок-схемы).

Графические (геометрические) информационные модели передают внешние признаки объекта — размеры, форму, цвет, расположение. В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы). Часто графические модели дополняются числами, символами и текстами (знаковыми элементами). В этом случае их называют смешанными моделями.

Образные модели представляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кинопленке и др.).  К ним относятся рисунки, фотографии.

Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. Схема – это графическое отображение состава и структуры сложной системы. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставле­ния информации об объекте. С помощью особых приёмов и графичес­ких обозначений на ней более рельефно выделяется один или не­сколько признаков рассматриваемого объекта.

В информатике особое место занимает построение блок-схем. Блок-схемы наглядно отражают алгоритм, т.е. последовательность действий при решении задачи. Они строятся при программировании – создании новых программ.

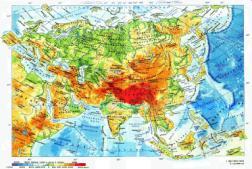
Карта описывает конкретную местность, которая является для нее объектом моделирования. Это уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений.

Карта создается с определенными целями для определения: местоположения населенных пунктов; рельефа местности; расположения автомагистралей; измерения расстояний между реальными объектами на местности  и т.д.

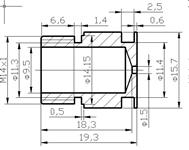
Чертеж – точная геометрическая копия реального объекта. Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения. Чертежи создаются конструкторами, проектировщиками, они должны быть очень точным, т.к. на них указываются все необходимые размеры реального объекта. Существует масса различных компьютерных сред для создания конструкторских чертежей: Автокад, Адем, Компас, 3D MАХ - для трехмерного моделирования и т.д.

Графики и диаграммы — это информационные модели, которые в наглядной форме представляют числовые и статистические данные.

График — линия, дающая наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График – отображение и визуализация различных процессов (природных, экономических, общественных и технических). График позволяет отслеживать динамику изменения данных.

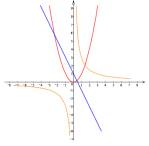
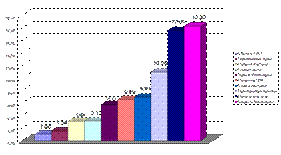
Диаграмма — графическое изображение, дающее наглядное пред­ставление о соотношении каких-либо величин или нескольких зна­чений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при из­учении электронных таблиц.

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. В информатике по графам строятся программы. В этом параграфе рассмотрены только самые основные понятия, свойства графов и некоторые способы решения задач.

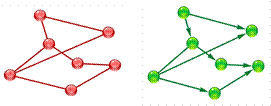
Если объекты некоторой системы изобразить точками (кругами, овалами, прямоугольниками…), а связи между ними — линиями (дугами, стрелками…), то мы получим информационную модель рассматриваемой системы в форме графа. Граф представляет собой набор вершин и соединяющих их ребер. Вершины графа могут быть обозначены буквами, числами, словами…

Если рёбра графа харак­теризуются некоторой дополнительной информацией (выраженной числами), его называют взвешенным, а числа - весами рёбер. Вес рёбер может соответствовать, например, расстоянию между объектами (городами).

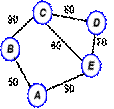
Если ребра графа указывают направление (представлены стрелками), то граф называют ориентированным (орграфом). Движение в ориентированном графе возможно тольеко в одном направлении (по стрелкам). Связи между объектами – вершинами в таком случае считаются несимметричными. У неориентированного графа связи между объектами – вершинами симметричны.

Одинаковые, но по-разному нарисованные графы, называют изоморфными. У изоморфных графов соединены одни и те же вершины.

Есть еще одно важное понятие, относящееся к графам – понятие связности. Граф называется связным, если любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.

Вершина, не имеющая рёбер, называется изолированной вершиной и составляет отдельную компоненту связности. Вершина, имеющая только одно ребро, называется концевой или висячей.

Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью (1). Цепь, начальная и конечная вершины которой совпадают, называется циклом (2). Дерево (иерархия) – это граф, в котором нет циклов (3), т. е. в нём нельзя из не­которой вершины пройти по нескольким различным рёбрам и вер­нуться в ту же вершину. Отличительной особенностью дерева явля­ется то, что между любыми двумя его вершинами существует един­ственный путь.

(1)                  (2)               (3)

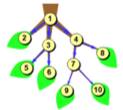
Всякая иерархическая система может быть представлена с по­мощью дерева. У дерева выделяется одна главная вершина, называе­мая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный им объект входит в один класс высше­го уровня. Любая вершина дерева может порождать несколько по­томков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не име­ющие порождённых вершин, называются листьями.

Например, родственные связи между членами семьи удобно изображать с по­мощью графа, называемого генеалогическим или родословным дере­вом.

Граф с циклом называется сетью. Если героев некоторого литера­турного произведения представить вершинами графа, а существую­щие между ними связи изобразить рёбрами, то мы получим граф, на­зываемый семантической сетью.