Tekisliklarning o‘zaro parallelligi

Tekisliklarning o‘zaro parallelligi

Agar Q tekislikka tegishli aÇb kesishuvchi to‘g‘ri chiziqlar ikkinchi P tekislikka tegishli a₁Çb₁ kesishuvchi to‘g‘ri chiziqlarga mos ravishda o‘zaro parallel bo‘lsa, bu tekisliklar ham o‘zaro parallel bo‘ladi. Ya’ni aÌQ, bÌQ bo‘lib, aÇb bo‘lsa va a₁ÌP va b₁ÌP bo‘lib a₁Çb₁ bo‘lsa hamda a || a₁, b||b₁ bo‘lganda Q || P bo‘ladi (95-rasm).

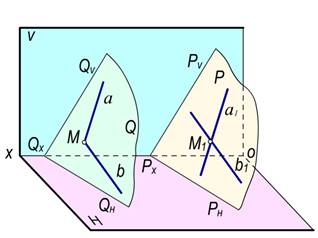
95-rasm

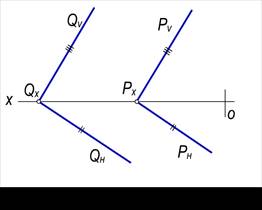
96-rasm                                                              97-rasm

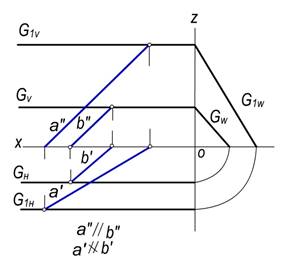
Chizmada profil proyeksiyalovchi tekisliklar uchun ularning gorizontal va frontal izlari parallel bo‘lishi yetarli bo‘lmaydi. Masalan, 97-rasmda berilgan G va G₁ tekisliklarda G_H||G_1H va G_V||G_1V bo‘lib, G_W∦G_1W bo‘lgani uchun G∦G₁ bo‘ladi. Bu tekisliklarning o‘zaro vaziyatini tekisliklarga tegishli a va b to‘g‘ri chiziqlar yordami bilan ham aniqlash mumkin, bunda aÌG₁ va bÌG bo‘lgan holda a″||b″ bo‘lsa, a′∦b′ bo‘lgani uchun a∦b va G∦G₁ bo‘ladi.

Fazodagi ixtiyoriy nuqta orqali berilgan tekislikka faqat bitta parallel tekislik o‘tkazish mumkin.

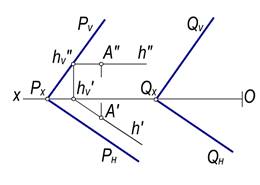
1-masala. A (A′, A″) nuqtadan Q (Q_H, Q_V) tekislikka parallel P(P_H, P_V) tekislik o‘tkazish talab qilinsin (98-a, rasm).

Echish. Tekisliklarning parallellik xususiyatlariga ko‘ra P tekislikning izlari P_H || Q_H va P_Y || Q_Y P_W || Q_W bo‘lishi shart. Misolni yechish uchun to‘g‘ri chiziq va tekislikning parallellik shartlaridan foydalanib, A nuqtaning A′ va A″ proyeksiyalaridan Q tekislikka parallel qilib ixtiyoriy to‘g‘ri chiziq, jumladan h (h′, h″) gorizontali o‘tkaziladi (4.31-b, rasm).

a)                                                                                  b)

98-rasm

Bu gorizontalning frontal izi h″_V yasalib, undan izlangan P tekislikning P_V izini berilgan tekislikning Q_V iziga parallel qilib o‘tkaziladi. So‘ngra P_VÇOx=P_X nuqtasidan Q tekislikning Q_H iziga parallel qilib izlangan tekislikning P_H izi o‘tkaziladi.

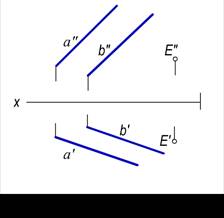
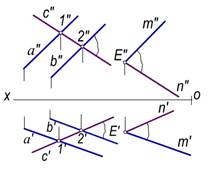
2-masala. E(E′, E″) nuqtadan a(a′, a″) va b(b′, b″) parallel chiziqlar bilan berilgan tekislikka parallel tekislik o‘tkazish talab qilinsin (99-a, rasm).

a)                                            99-rasm                                                     b)

Echish. Berilgan (a∥b) tekislikka tegishli ixtiyoriy c(c′, c″) to‘g‘ri chiziqni o‘tkazib, so‘ngra E nuqtaning E′ va E″ proyeksiyalaridan a va s chiziqlar proyeksiyalariga mos ravishda parallel qilib o‘tkazilgan m′Çn′, m″Çn″ kesishuvchi chiziqlar proyeksiyalari izlangan tekislik proyeksiyasi bo‘ladi.

Tekislikka tegishli bo‘lmagan nuqtadan mazkur tekislikka parallel bo‘lgan cheksiz ko‘p to‘g‘ri chiziqlar o‘tkazish mumkin. Bunday to‘g‘ri chiziqlar to‘plami berilgan tekislikka parallel bo‘lgan tekislikni ifodalaydi.[1]

Скачано с www.znanio.ru