Тема 2.2. Представление информации в компьютере

Тема 2.2. Представление информации в компьютере.

Задание 1. Прочитайте материал темы по учебнику (стр.50-62) и конспекту лекций. Выучите основные понятия и определения (система счисления, основание системы счисления, алфавит системы счисления, позиционные и непозиционные системы счисления) и алгоритмы перевода чисел.

Задание 2. Подготовьте сообщение на тему «Применение ПК в профессии медика».

Задание 3. Пользуясь теоретическим материалом о системах счисления, выполните следующие задания:

1. Запишите число в развернутой форме: 3670,294₁₀.

2. Выполните перевод чисел из одной системы счисления в другую:

243,52₁₀ – в двоичную, восьмеричную, шестнадцатеричную системы счисления с точностью до трех знаков после запятой;

1110001010₂ – в восьмеричную, десятичную, шестнадцатеричную системы счисления;

742,3₈ - в двоичную, десятичную системы счисления;

1В9₁₆ - в двоичную, восьмеричную, десятичную системы счисления.

3. Запишите число в римской системе счисления: 329.

Теоретический материал:

Пример развернутой записи десятичного числа:

247,32 = 2*10² + 4*10¹ + 7*10⁰ + 3*10^-1 + 2*10^-2.

Развернутая форма служит для перевода чисел из любой системы счисления в десятичную. Например:

423,312₅ = 4*5² + 2*5¹+ 3*5⁰+ 3*5^-1+1*5^-2 +2*5^-3 = 113,016512₁₀.

Алгоритм перевода чисел из десятичной системы счисления в другие выполняется следующим образом:

1)        Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы, до тех пор, пока не получится частное, меньшее делителя (то есть меньше 2, или 8, или 16). Записать полученные остатки в обратной последовательности, а слева добавить последнее частное (см. пример на рис. 2).

2)        Последовательно выполнять умножение исходной десятичной дроби и получаемых дробных частей произведений на основание системы (на 2, или 8, или 16) до тех пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычислений. Записать полученные целые части произведения в прямой последовательности (см. пример на рис. 3).

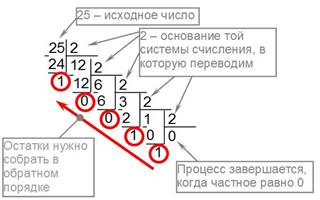
Рисунок 2. Пример перевода целого десятичного числа в двоичную систему счисления

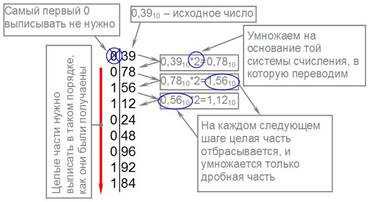
Рисунок 3. Пример перевода дробной части десятичного числа в двоичную систему счисления

Если основание q-ичной системы счисления является степенью  числа 2, то  перевод  чисел из q-ичной системы счисления в 2-ичную и обратно можно проводить по более простым правилам. Для того чтобы целое двоичное число записать в системе счисления с основанием q=2n, нужно:

1)        Целое двоичное число разбить справа налево на группы по n  цифр в каждой, а дробную часть разбить слева направо на группы по n цифр в каждой.

2)        Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

3)        Рассмотреть каждую группу как n-разрядное двоичное число и  записать ее соответствующей цифрой в системе счисления с основанием q=2n.

Например, переведем число 101100001000110010₂ сначала в восьмеричную систему счисления:

Рисунок 4. Пример перевода двоичного числа в восьмеричное

затем в шестнадцатеричную;

Рисунок 5. Пример перевода двоичного числа в шестнадцатеричное

Получим: 101100001000110010₂ = 541062₈ = 200F87₁₆.