Тема урока: Показательная функция, её свойства и график (1-й урок)

Тема урока: Показательная функция, её свойства и график
(1-ый урок из 2-х).
Цели урока:
Учебная:
- научить строить графики показательных функций с разными основаниями;
- научить определять свойства показательной функции по её графику;
- показать практическое применение показательной функции в жизни и в других науках.
Развивающая:
- совершенствовать умения сравнивать, анализировать, обобщать;
- развивать логическое мышление, внимание и умение работать в проблемной ситуации.
Воспитательная:
- развитие познавательного интереса к учебной дисциплине;
- формирование точности и аккуратности при построении чертежей;
- развитие творческого отношения к учебной деятельности.
Методическая: совершенствование методики использования интерактивных методов обучения.
Задачи урока:
- научить строить простейшие графики показательной функции и решать показательные уравнения графически,
- научить применят свойства показательной функции;
- осуществлять контроль знаний;
- использовать различные приемы и методы для поддержания работоспособности студентов;
- предоставить студентам возможность совершенствования коммуникативных компетентностей.
Мотивация учебной деятельности: Создание условий для формирования образовательных компетенций (коммуникативных, креативных, учебно-познавательных и др.) студентов в предметной области Математика (Алгебра и начала анализа) по теме «Показательная функция, её свойства и график» через их включение в продуктивную и осознанную деятельность по отношению к объектам реальной действительности.
|
Тип урока: |
Урок изучения нового материала |
|
Вид урока: |
Интерактивный |
|
Методы обучения: |
Проблемный, ИКТ технологии, интерактивные: работа в группе, взаимоконтроль, творческая работа, самоконтроль, рефлексия. |
|
Дидактическое обеспечение: |
Программу Мicrosoft Office Excel, презентация по теме урока, презентация студента, учебная программа, рабочая программа, календарно-тематический план, план урока, опорный конспект, конспект для оценивания знаний. |
|
Межпредметные связи: |
Информатика и ИКТ, биология, физика |
|
Формы организации учебной деятельности студентов: |
Фронтальный опрос, элементы беседы, работа в группах, решение проблемной задачи, тестирование, выполнение индивидуальных творческих заданий, комплексный подход к оценке знаний. |
|
Место проведения урока: |
Кабинет информатики и ИКТ |
|
Время проведения: |
45 минут |
Ход урока:
|
1. Этап: Организационный момент. |
2 мин. |
|
2. Этап: Актуализация, мотивация обучения. |
5 мин. |
|
3. Этап: Формулирование темы и цели. |
1 мин. |
|
4. Этап: Объяснение нового материала и первичное закрепление материала. |
8 мин. |
|
5. Этап: Применение новых знаний в нестандартных ситуациях. |
12 мин. |
|
6. Этап: Творческие упражнения. |
8 мин. |
|
7. Этап: Тестирование. |
5 мин. |
|
8. Этап: Итоги урока. Рефлексия. |
3 мин. |
|
9. Этап: Домашнее задание. |
1 мин. |
Математика – это язык,
на котором написана книга природы.
Галилео Галилей
Ход урока.
1. Этап: Организационный момент.
Преподаватель:
Добрый день, уважаемые гости, преподаватели, студенты. Рада приветствовать вас на уроке. Давайте пожелаем друг другу и нашим гостям хорошего настроения.
Желаю вам удачи и прекрасных результатов! Проверка состава студентов.
Какой вопрос вы задаете, когда идете на урок математики?
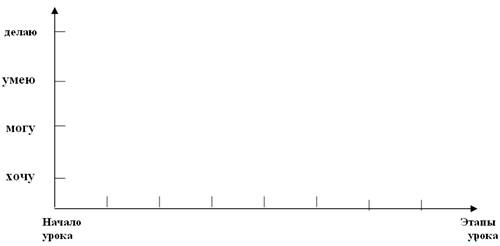
(На доске в столбик записаны слова: хочу, могу, умею, делаю) преподаватель, показывая на каждое из этих слов, даёт расшифровку. (Слайд №1).
ХОЧУ: …. пожелать вам увеличение объёма знаний.
МОГУ:…… разрешить на уроке ошибаться, сомневаться, консультироваться, договариваться.
УМЕЮ: …. применять рациональные способы для решения задач.
ДЕЛАЮ: …. Себе и вам установку «Понять и быть тем первым, который увидит ход решения».
Притча. У Плутарха есть известная притча о работниках, которые везли тачки с камнями. Работников было трое. К ним подошёл человек и задал каждому из них один и тот же вопрос: «Чем ты занимаешься?» Ответ первого был таков: «Везу эту проклятую тачку». По-иному ответил второй: «Зарабатываю себе на хлеб». Третий воодушевлённо провозгласил: «Строю прекрасный храм!»
Как вы думаете: зачем прозвучала именно эта притча сейчас?
Перед вами лежат листы самооценки. Подпишите их. На каждом этапе работы прошу вас оценить свои возможности (Приложение №1)
2. Этап: Актуализация, мотивация обучения.
Преподаватель:
А знаете ли вы, что с достаточной точностью можно вычислить количество болезнетворных бактерий при попадании их в благоприятную среду? Например, когда человек болеет. Или можно подсчитать количество особей, в какой-либо популяции животных через определённый промежуток времени? Или узнать, сколько будет денег на вкладе у вас через 5 лет, если вы положите, например 100 тысяч рублей под срочные проценты в банк?
Оказывается эти и другие задачи можно решить с помощью показательной функции. Записываем в тетрадь дату и тему занятия «Показательная функция, её свойства и график».
Игра «Самый умный на уроке» (Слайд №2).
Эта игра проводится с целью актуализации знаний студентов на уроке изучения нового материала по теме «Показательная функция и ее график».
Студентам предлагается в течение 60 секунд отвечать на вопросы (Приложение №2)
Звание «самого умного на уроке» присваивается тому, кто ответил на большее количество вопросов.
Вопросы:
1) Независимая переменная (х)
2) График четной функции симметричен относительно чего (Оу)
3) График квадратичной функции называется (парабола)
4) Как обозначается область определения? (D )
5) График какой функции - прямая (линейной)
6) О какой функции речь? Чем больше х, тем больше у. (возрастающая)
7) Свойство функции f(-x) = f(x ) (четность)
8) График нечетной функции симметричен относительно чего
(начала координат)
9) О чем речь? Чем меньше х, тем больше у. (убывание)
10) Множество целых чисел - какая буква? (Z)
11) Множество действительных чисел –какая буква? (R)
12) Свойство функции f(-x) = - f(x) (нечетность).
3. Этап: Формулирование темы и цели. (Слайд №3, 4).
Преподаватель. В конце 17 века математик, Иоганн Бернулли, рассмотрел степени с переменным действительным показателем, т.е. ввёл понятие показательной функции. И поэтому цели нашего урока таковы:
- научиться строить графики показательных функций с разными основаниями;
- научиться определять свойства показательной функции по её графику;
- показать практическое применение показательной функции в жизни и в других науках.
4. Этап: Объяснение нового материала и первичное закрепление материала. (Слайд №5)
Определение: Функция вида y=ax, где а-фиксированное положительное число, a>0; a≠1, называется показательной функцией с основанием a.
- Как вы думаете, почему основание степени не может быть равным 1, или меньше 0?
(Предполагаемый ответ: т. к. 1 в любой степени равна 1, а при возведении отрицательного числа в дробную степень на множестве действительных чисел решений нет).
Запишем определение в тетрадь.
Сейчас мы с вами построим график функции на компьютере с помощью программы МO Excel, а затем каждый из вас построит график в тетради. (Слайд №6).
Работа на компьютере: набираем таблицу для построения графиков функций y=2x и y=(1/2)x. (Приложение №3).
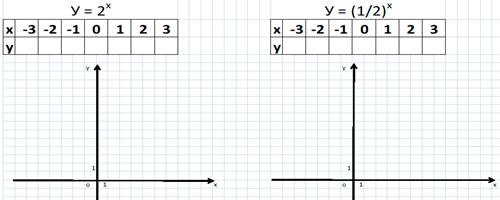
Студент сначала заполняет первую таблицу и по таблице построит график функции в программе табличного редактора. Один студент строит на компьютере, все проверяют правильность построения. Затем все строят в своих тетрадях. После этого все вместе заполняем вторую таблицу и студент строит на компьютере вторую функцию. (Преподаватель обращает внимание на правильность и аккуратность построения.)
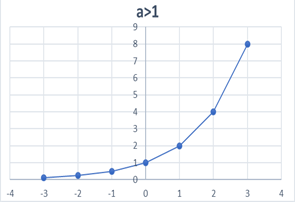
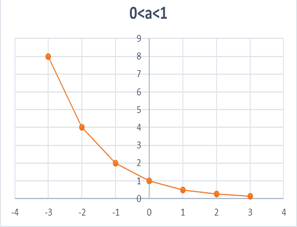
- Давайте определим по графику основные свойства показательной функции. Я напомню, что мы должны найти область определения функции D(x), множество значений функции E(y), промежутки монотонности функции, её экстремумы, выяснить чётность и периодичность. Все результаты будем записывать в тетрадях. (Преподаватель обращает внимание на правильность и аккуратность построения.)
Внимание. Основные свойства показательной функции: (Слайд №7).
1. D(x): (-∞;+∞);
2. E(y): (0;+∞);
3. Функция монотонно возрастает, если a>1, и монотонно убывает, если 0<a<1.
4. Графики всех показательных функций проходят через точку А(0;1).
5. Почему все показательные функции проходят через эту точку? (Предполагаемый ответ: т.к. любое число в нулевой степени равно 1).
6. Функция не имеет экстремумов, не периодическая, не является ни чётной ни нечётной.
5. Применение новых знаний в нестандартных ситуациях.
№201 (4). Построить график функции: у= 3х-2
Ответьте на вопросы:
1. Найдите область определения и множество значений функции.
2. Выяснить: функция убывает или возрастает. Почему?
6. Этап: Творческое упражнение.
Решить графически уравнение: 3х = 4 – х. (Слайд №9). (Приложение№4).
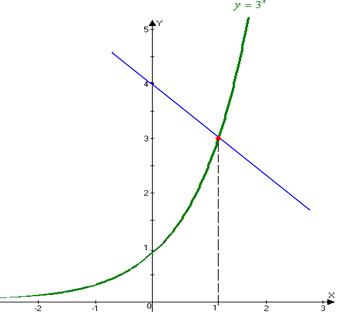
Используем функционально-графический метод решения уравнений: построим в одной системе координат графики функций у=3х и у=4-х.
Замечаем, что они имеют одну общую точку (1;3).
Значит, уравнение имеет единственный корень х=1. Ответ: 1
Решите графически уравнения: (Слайд №10).
(1/2)х = х+3; Ответы: -1.
У меня есть задания для вас они перед вами. (Работаем в группах.) (Слайд №11). (Приложение№5).
Задание №1
1. Постройте в одной системе координат графики функций f(x) = 2х–2 , f(x) = 2х-2 – 1
2. Какие вопросы можно составить к этому рисунку? Дайте обоснованный ответы на составленные вопросы?
Задание №2
1. Постройте в одной системе координат графики функций f(x) = 2х+2 , f(x) = 2х + 4
2. Какие вопросы можно составить к этому рисунку? Дайте обоснованный ответы на составленные вопросы?
Время работы 5 минут. Вы можете задать только один вопрос.
7.Этап: Самостоятельная работа. (Приложение №6).
Студентам выдаются тестовые задания.
1 вариант (Слайд №12).
По данному графику показательной функции y=3x -2 нужно:
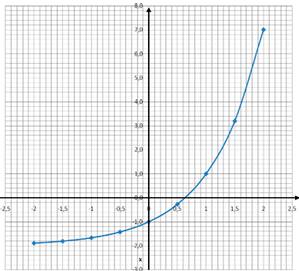
|
Номер задания |
Задание |
Ответы |
||
|
А |
Б |
В |
||
|
1. |
Найти область определения функции. |
(-∞;+∞) |
(-2;+∞) |
(-∞;3) |
|
2. |
Найти множество значений функции. |
(-∞;+∞) |
(-∞;3) |
(-2;+∞) |
|
3. |
Определить монотонность функции. |
возрастает |
убывает |
не возрастает и не убывает |
|
4. |
Найти значение функции, если значение аргумента равно 2. |
Y=1 |
Y=3 |
Y=7 |
|
5. |
Найти значение аргумента, если значение функции равно 1. |
X=0 |
X=1 |
X=5 |
2 вариант (Слайд №13).
По данному графику показательной функции y=(1/2)x + 2 нужно:
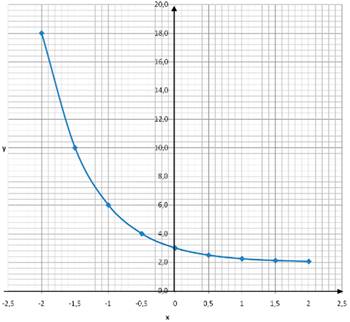
|
Номер задания |
Задание |
Ответы |
||
|
А |
Б |
В |
||
|
1. |
Найти область определения функции. |
(-∞;+∞) |
(-2;+∞) |
(2;+∞) |
|
2. |
Найти множество значений функции. |
(-∞;+∞) |
(-∞;3) |
(2;+∞) |
|
3. |
Определить монотонность функции. |
возрастает |
убывает |
не возрастает и не убывает |
|
4. |
Найти значение функции, если значение аргумента равно 2. |
Y=1 |
Y=3 |
Y=4 |
|
5. |
Найти значение аргумента, если значение функции равно 3. |
X=0 |
X=1 |
X=5 |
Критерии оценок: количество правильно выполненных заданий - заработанная оценка преподаватель объявляет студентам.
После выполнения заданий студенты меняются своими работами, на доске появляются варианты с правильными ответами, выделенными цветом.
Ответы: 1 вариант (Слайд №14)
|
№ п/п |
Задание |
1 вариант y=3x - 2 |
2 вариант y=(1/2)x + 2 |
|
1. |
Найти область определения функции. |
а |
а |
|
2. |
Найти множество значений функции. |
в |
в |
|
3. |
Определить монотонность функции. |
б |
б |
|
4. |
Найти значение функции, если значение аргумента равно 2. |
в |
в |
|
5. |
Найти значение аргумента, если значение функции равно 3. |
б |
а |
Студенты оценивают свою работу и полученные знания, поднимая карточки разного цвета и формы:
- «красная карточка» - отлично
- «зелёная карточка» - хорошо
- «жёлтая карточка - удовлетворительно
- «белая карточка» - неудовлетворительно
Предлагаем послушать сообщение студента «Применение показательной функции»
8. Этап: Итоги урока. Рефлексия.
Подведём итоги. (Слайд 15)
Кто желает продемонстрировать свой график уравнения? Какого вида график у вас получился? Поднимите руку те, у кого получилась возрастающая функция? Что это значит?
Вывод:
- Показательная функция имеет вид у=ах , где а>0; а≠1.
- Возрастает, если а>1, и убывает, если 0<a<1;
- Используется при решении многих практических задач.
Посчитайте свои баллы. Выставьте себе оценки.
“5” – максимум баллов, “4” – меньше от максимума на 2 балла, “3” – 5-6 баллов.
Рефлексия.
- На уроке по этой теме я узнал: ____.
- На уроке по этой теме я научился: ____.
- Лучше всего у меня получалось: ____.
- Основные трудности при изучении темы: ____.
- Что бы я изменил на уроке, чтобы улучшить свои результаты: ____.
9. Этап: Домашнее задание. §11, №194, №201(2,3). (Слайд 16)
Приложение №1
Ф.И. студента ___________________________________________
Приложение №2
Игра «Самый умный на уроке»
|
№ п/п |
Вопрос |
Ответ |
|
1 |
Независимая переменная
|
|
|
2 |
График четной функции симметричен относительно чего |
|
|
3 |
График квадратичной функции называется |
|
|
4 |
Что обозначают буквой D |
|
|
5 |
График какой функции - прямая |
|
|
6 |
О какой функции речь? Чем больше х, тем больше у. |
|
|
7 |
Свойство функции f(-x) = f(x ) |
|
|
8 |
График нечетной функции симметричен относительно чего |
|
|
9 |
О чем речь? Чем меньше х, тем больше у. |
|
|
10 |
Множество целых чисел - какая буква? |
|
|
11 |
Множество действительных чисел –какая буква? |
|
|
12 |
Свойство функции f(-x) = - f(x) |
|
Приложение №3
Таблица для построения графиков функций y=2x и y=(1/2)x.
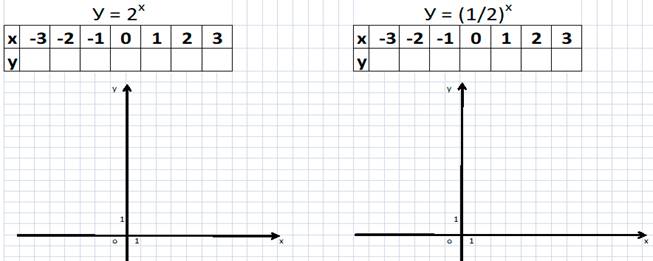
Основные свойства показательной функции:
1. D(x)=(-∞;+∞);
2. E(y)=(0;+∞);
3. Функция монотонно возрастает, если a>1, и монотонно убывает, если 0<a<1.
4. Графики всех показательных функций проходят через точку А(0;1).
5. Почему все показательные функции проходят через эту точку? (Предполагаемый ответ: т.к. любое число в нулевой степени равно 1).
6. Функция не имеет экстремумов, не периодическая, не является ни чётной ни нечётной.
Приложение №4
Творческое задание.
Решить графически уравнение: 3х = 4 – х.
Решите графически уравнения: (1/2)х = х + 3;
Приложение №5
В группах:
Задание №1
1. Постройте в одной системе координат графики функций f(x) = 2х–2 , f(x) = 2х – 1
2. Какие вопросы можно составить к этому рисунку? Дайте обоснованный ответы на составленные вопросы?
Задание №2
1. Постройте в одной системе координат графики функций f(x) = 2х+2 , f(x) = 2х + 4
2.Какие вопросы можно составить к этому рисунку? Дайте обоснованный ответы на составленные вопросы?
Приложение №6
Самостоятельная работа.
Ответить на тест.
1 вариант
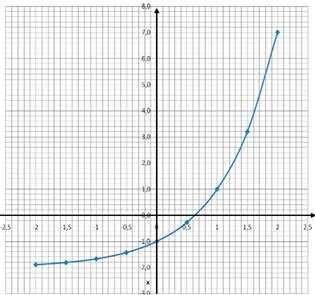
По данному графику показательной функции y=3x-2 нужно:
|
Номер задания |
Задание |
Ответы |
||
|
А |
Б |
В |
||
|
1. |
Найти область определения функции. |
(-∞;+∞) |
(-2;+∞) |
(-∞;3) |
|
2. |
Найти множество значений функции. |
(-∞;+∞) |
(-∞;3) |
(-2;+∞) |
|
3. |
Определить монотонность функции. |
возрастает |
убывает |
не возрастает и не убывает |
|
4. |
Найти значение функции, если значение аргумента равно 2. |
Y=1 |
Y=3 |
Y=7 |
|
5. |
Найти значение аргумента, если значение функции равно 1. |
X=0 |
X=1 |
X=5 |
2 вариант
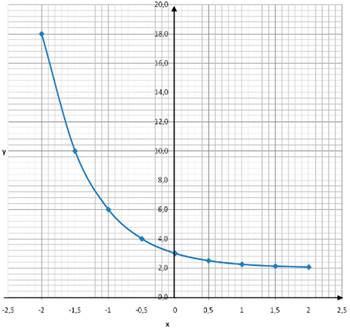
По данному графику показательной функции y=(1/4)x + 2 нужно:
|
Номер задания |
Задание |
Ответы |
||
|
А |
Б |
В |
||
|
1. |
Найти область определения функции. |
(-∞;+∞) |
(-2;+∞) |
(2;+∞) |
|
2. |
Найти множество значений функции. |
(-∞;+∞) |
(-∞;3) |
(2;+∞) |
|
3. |
Определить монотонность функции. |
возрастает |
убывает |
не возрастает и не убывает |
|
4. |
Найти значение функции, если значение аргумента равно -1. |
Y=1 |
Y=3 |
Y=6 |
|
5. |
Найти значение аргумента, если значение функции равно 3. |
X=0 |
X=1 |
X=5 |
Критерии оценок: количество правильно выполненных заданий - заработанная оценка преподаватель объявляет студентам.
После выполнения заданий студенты меняются своими работами, на доске появляются варианты с правильными ответами, выделенными цветом.
© ООО «Знанио»
С вами с 2009 года.
![]()

