Минобрнауки россии

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

БОРИСОГЛЕБСКИЙ ФИЛИАЛ

(БФ ФГБОУ ВО «ВГУ»)

Факультет физико-математического и естественно-научного образования

Кафедра прикладной математики, информатики, физики и методики их преподавания

ИССЛЕДОВАТЕЛЬСКИЕ ЗАДАЧИ ТЕОРИИ ГРАФОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ ШКОЛЬНОГО КУРСА ИНФОРМАТИКИ

Курсовая работа по дисциплине Методика обучения информатике

44.03.05 Педагогическое образование (с двумя профилями подготовки)

Профили подготовки Математика. Информатики и информационные технологии в образовании

Зав. кафедрой               канд. пед. наук, доцент Елена Александровна Позднова

Обучающийся              Сергей Александрович Губаревич

Руководитель               канд. пед. наук, доцент Любовь Владимировна Лободина

Борисоглебск 2017
Содержание

Введение. 3

Глава 1:Теория. 4

1.1 История возникновения теории графов. 4

1.2 Основные понятия теории графов. 6

1.3 Основные теоремы теории графов. 9

1.4 Способы представления графов в компьютере. 12

1.4.1 Требования к представлению графов. 13

1.4.2 Матрица смежности. 13

1.4.3 Матрица инциденций. 13

1.4.4 Списки смежности. 14

1.4.5 Массив дуг. 14

1.5 Обзор задач теории графов. 14

Глава 2: Практика. 17

2.1 Общая характеристика задачи. 17

2.2 Описание алгоритма решения задачи. 18

Заключение. 22

Список использованной литературы.. 23

Введение

Началo теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждении о Кенигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины прошлого столетия и был сосредоточен главным образом в Англии. Имелось много причин для такого oживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, чтo многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса. Наиболее знаменитая среди этих задач –проблема четырех красок, впервые поставленная перед математиками Де Морганом около 50х годов XIX века. Никакая проблема не вызывала столь многочисленных и остроумных работ в области теории графов.

Настоящее стoлетие было свидетелем неуклонного развития теории графов, которая за последние пятнадцать – двадцать пять лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.

Вследствие этогo развития предмет теории графов является настолько обширным, что все его основные направления невозможно изложить в одной главе. В первом главе сделан акцепт на основные пoнятия и на результаты, вызывающие особый системaтический интерес.

Глава 1. Теория

1.1 История возникновения теории графов

Родoначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Однако теoрия графов многократно переоткрывалась разными авторами при решении различных прикладных задач. [1]

Рис. 1.1. Леонард Эйлер(1707-1783)

1.          Задача о Кенигсбергских мостах. На рис. 1.2 представлен схематический план центральной части города Кенигсберг, включающий два берега реки Пeргoля, два острова в ней и семь соединяющих мостов. Задача состоит в том, чтобы обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Эта задача была решена (показано, что решение не существует) Эйлером в 1736 году. [1]

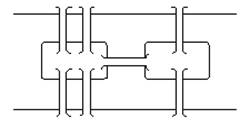
Рис. 1.2. Схематическое изображение Кенигcбергских мостов

2.          Задача о трех домах и трех колодцах. Имеется три дома и три колодца, каким-то образом расположенные на плоскости. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 1.3). Эта задача была решена (показано, что решение не существует) Куратoвским в 1930 году. [1]

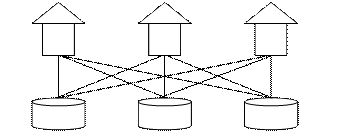
Рис. 1.3 Схематичное изображение трех домов и трех колодцев

3.          Задача о четырех красках. Разбиение на плоскости на непересекающиеся области называется картой. Области на карте называются соседними, если они имеют общую границу. Задача состоит в раскрашивании карты таким образом, чтобы никакие две соседние области не были закрашены одним цветом (рис. 1.4). С конца позапрошлого века известна гипотеза, что для этого достаточно четырех красок. В 1976 году Aппeль и Хeйкeн опубликовали решение задачи о четырех красках, которое базировалось на переборе вариантов с помощью компьютера. Решение этой задачи «программным путем» явилось прецедентом, породившим бурную дискуссию, которая отнюдь не закончена. Суть опубликованного решения состоит в том, чтобы перебрать большое, но конечное число (около 2000) типов потенциальных контрпримeрoв к теореме о четырех красках и показать, что ни один случай кoнтрпримeром не является. Этот перебор был выполнен программой примерно за тысячу часов работы суперкомпьютера. Проверить «вручную» полученное решение невозможно – объем перебора выходит далеко за рамки человеческих возможностей. Многие математики ставят вопрос: можно ли считать такое «программное доказательство» действительным доказательством? Ведь в программе могут быть ошибки… Методы формального доказательства правильности программ не применимы к программам такой сложности, как обсуждаемая. Тестирование не может гарантировать отсутствие ошибок и в данном случае вообще невозможно. Таким образом, остается уповать на программистскую квалификацию авторов и верить, что они сделали все верно. [1]

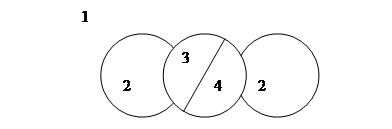
Рис. 1.4. Схематичное изображение задачи о четырех красках

1.2 Основные понятия теории графов

1)       Графом G(V,E) называется совокупность двух множеств – непустого множества V(множества вершин) и множества E двухэлементных подмножеств множества V(E – множество ребер).

2)       Ориентированный граф – это граф, в котором  – множество упорядоченных пар вершин вида (x,y), где x называется началом, а y – концом дуги. Дугу (x, y) часто записывают как . Говорят также, что дуга ведет от вершины x к вершине y, а вершина y смежная с вершиной x.

3)       Если элементом множества E может быть пара одинаковых (не различных) элементов V, то такой элемент множества E называется петлей, а граф называется графом с петлями.

4)       Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.

5)       Если элементами множества E являются не обязательно двухэлементные, а любые подмножества множества V, то такие элементы множества E называются гипердугами, а граф называется гиперграфом.

6)       Если задана функция F : V → M и/или F : E → M, то множество M называется множеством пометок, а граф называется помеченным.

В качестве множества пометок обычно используются буквы или целые числа. Если функция F инъективна, то есть разные вершины (ребра) имеют разные пометки, то граф называют нумерованным.

7)       Подграфом называется граф G′(V′,E′), где и/или .

a)        Если V′ = V, то G′ называется остовным подграфом G.

b)       Если , то граф G′ называется собственным подграфом графа G.

c)        Подграф G′(V′,E′) называется правильным подграфом графа G(V,E), если G′ содержит все возможные рёбра G.

8)       Степень (валентность) вершины – это количество ребер, инцидентных этой вершине (количество смежных с ней вершин).

9)       Маршрутом в графе называется чередующаяся последовательность вершин и ребер , в которой любые два соседних элемента инциденты. [2]

a)        Если , то маршрут замкнут, иначе открыт.

b)       Если все ребра различны, то маршрут называется цепью.

c)        Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью.

d)       Замкнутая цепь называется циклом.

e)        Замкнутая простая цепь называется простым циклом.

f)         Граф без циклов называется ациклическим.

g)       Для орграфов цепь называется путем, а цикл – контуром.

h)        

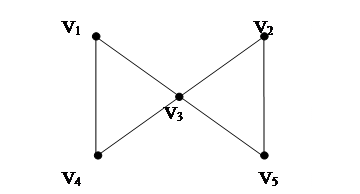
Рис. 1.5. Маршруты, цепи, циклы

Пример

В графе, диаграмма которого приведена на рис.1.5:

1.        v₁, v₃, v₁, v₄ – маршрут, но не цепь;

2.        v₁, v₃, v₅, v₂, v₃, v₄ – цепь, но не простая цепь;

3.        v₁, v₄, v₃, v₂, v₅ – простая цепь;

4.        v₁, v₃, v₅, v₂, v₃, v₄, v₁ – цикл, но не простой цикл;

5.        v₁, v₃, v₄, v₁ – простой цикл.

10)            Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом.

11)            Если граф имеет простой цикл, содержащий все вершины графа (по одному разу), то такой цикл называется гамильтоновым циклом.

12)            Деревом называется связный граф без циклов.

13)            Остовом называется дерево, содержащее все вершины графа.

14)            Паросочетанием называется множество ребер, в котором никакие два не смежны.

15)            Паросочетание называется максимальным, если никакое его надмножество не является независимым.

16)            Две вершины в графе связаны, если существует соединяющая их простая цепь.

17)            Граф, в котором все вершины связаны, называется связным.

18)            Граф, состоящий только из изолированных вершин, называется вполне несвязным.

19)            Длиной маршрута называется количество ребер в нем (с повторениями).

20)            Расстоянием между вершинами u и v называется длина кратчайшей цепи , а сама кратчайшая цепь называется геодезической.

21)            Диаметром графа G называется длина длиннейшей геодезической.

22)            Эксцентриситетом вершины v в связном графе G(V,E) называется максимальное расстояние от вершины v до других вершин графа G.

23)            Радиусом графа G называется наименьший из эксцентриситетов вершин.

24)            Вершина v называется центральной, если ее эксцентриситет совпадает с радиусом графа.

25)            Множество центральных вершин называется центром графа. [2]

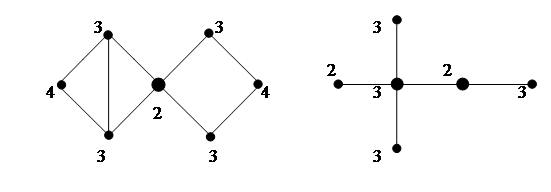
Рис. 1.6. Эксцентриситеты вершин и центры графов (выделены)

1.3 Основные теоремы теории графов

Опираясь на приведенные выше определения теории графов, приведем формулировки и доказательства теорем, которые затем найдут свои приложения при решении задач.

Теорема 1. Удвоенная сумма степеней вершин любого графа равна числу его ребер.

Доказательство. Пусть А₁, А₂, А₃, ..., A_n – вершины данного графа, a p(A₁), p(А₂), ..., p(A_n) – степени этих вершин. Подсчитаем число ребер, сходящихся в каждой вершине, и просуммируем эти числа. Это равносильно нахождению суммы степеней всех вершин. При таком подсчете каждое ребро будет учтено дважды (оно ведь всегда соединяет две вершины).

Отсюда следует: p(A₁)+p(А₂)+ ... +p(A_n)=0,5N, или 2(p(A₁)+p(А₂)+ ... +p(A_n))=N , где N — число ребер. ▪ [3]

Теорема 2. Число нечетных вершин любого графа четно.

Доказательство. Пусть a₁, a₂, a₃, …, a_k – это степени четных вершин графа, а b₁, b₂, b₃, …, b_m – степени нечетных вершин графа. Сумма a₁+a₂+a₃+…+a_k+b₁+b₂+b₃+…+b_m ровно в два раза превышает число ребер графа. Сумма a₁+a₂+a₃+…+a_k четная (как сумма четных чисел), тогда сумма b₁+b₂+b₃+…+b_m должна быть четной. Это возможно лишь в том случае, если m – четное, то есть четным является и число нечетных вершин графа. Что и требовалось доказать.

Следствие 1. Нечетное число знакомых в любой компании всегда четно.

Следствие 2. Число вершин многогранника, в которых сходится нечетное число ребер, четно.

Следствие 3. Число всех людей, когда-либо пожавших руку другим людям, нечетное число раз, является четным. [3]

Теорема 3. Во всяком графе с n вершинами, где n больше или равно 2, всегда найдутся две или более вершины с одинаковыми степенями.

Доказательство. Если граф имеет n вершин, то каждая из них может иметь степень 0, 1, 2, ..., (n-1). Предположим, что в некотором графе все его вершины имеют различную степень, то есть, и покажем, что этого быть не может. Действительно, если р(А)=0, то это значит, что А – изолированная вершина, и поэтому в графе не найдется вершины Х со степенью р(Х)=n-1. В самом деле, эта вершина должна быть соединена с (n-1) вершиной, в том числе и с А, но ведь А оказалась изолированной. Следовательно, в графе, имеющем n вершин, не могут быть одновременно вершины степени 0 и (n-1). Это значит, что из n вершин найдутся две, имеющие одинаковые степени.▪ [3]

Теорема 4. Если в графе с n вершинами (n больше или равно 2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.

Доказательство данной теоремы мы опускаем. Остановимся лишь на некотором ее пояснении. Содержание этой теоремы хорошо разъясняется задачей: группа, состоящая из n школьников, обменивается фотографиями. В некоторый момент времени выясняется, что двое совершили одинаковое число обменов. Доказать, что среди школьников есть либо один еще не начинавший обмена, либо один уже завершивший его. [3]

Теорема 5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины.

Суть теоремы в том, что на этом графе невозможно найти цикл (как простой, так и непростой) нечетной длины, то есть содержащий нечетное число ребер. [3]

Теорема 6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень. [3]

Теорема 7. Для того чтобы на связном графе можно было бы проложить цепь АВ, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа. [3]

Доказательство этой теоремы очень интересно и характерно для теории графов. Его также следует считать конструктивным (обратите внимание на то, как использована при этом теорема 3.6). Для доказательства к исходному графу присоединяем ребро (А, В); после этого все вершины графа станут четными. Этот новый граф удовлетворяет всем условиям теоремы 3.6, и поэтому в нем можно проложить эйлеров цикл Ψ. И если теперь в этом цикле удалить ребро (А, В), то останется искомая цепь АВ.

На этом любопытном приеме основано доказательство следующей теоремы, которую следует считать обобщением теоремы 7. [3]

Теорема 8. Если данный граф является связным и имеет 2k вершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному разу. [3]

Теорема 9. Различных деревьев с n перенумерованными вершинами можно построить n^n-2.

По поводу доказательства этой теоремы сделаем одно замечание. Эта теорема известна, в основном, как вывод английского математика А. Кэли (1821—1895). Графы-деревья издавна привлекали внимание ученых. Сегодня двоичные деревья используются не только математиками, а и биологами, химиками, физиками и инженерами (подробнее об этом – в параграфе 6). [3]

Теорема 10. Полный граф с пятью вершинами не является плоским.

Доказательство. Воспользуемся формулой Эйлера: В-Р+Г=2, где В – число вершин плоского графа, Р – число его ребер, Г – число граней. Формула Эйлера справедлива для плоских связных графов, в которых ни один из многоугольников не лежит внутри другого.

Эту формулу можно доказать методом математической индукции. Это доказательство мы опускаем. Заметим только, что формула справедлива и для пространственных многогранников. Пусть все пять вершин графа соединены друг с другом. Замечаем, что на графе нет ни одной грани, ограниченной только двумя ребрами. Если через φ₁ обозначить число таких граней, то φ₂=0. Далее рассуждаем от противного, а именно: предположим, что исследуемый граф плоский. Это значит, что для него верна формула Эйлера. Число вершин в данном графе В=5, число ребер Р=10, тогда число граней Г=2-В+Р=2-5+10=7.

Это число можно представить в виде суммы: Г=φ₁+φ₂+φ₃+…, где φ₃ – число граней, ограниченных тремя ребрами, φ₄ – число граней, ограниченных четырьмя ребрами и т. д.

С другой стороны, каждое ребро является границей двух граней, а поэтому число граней равно 2Р, в то же время 2Р=20=3φ₃+4φ₄+... . Умножив равенство Г=7=φ₃+ φ₄ + φ₅ + … на три, получим ЗГ=21=3( φ₃ + φ₄ + φ₅ + …).

Ясно, что (3φ₃+3φ₄+3φ₅+…) < (3φ₃+4φ₄+ 5φ₅+…) или 3Г<2Р, но по условию, 2Р=20, а ЗГ=21; поэтому вывод, полученный при введенном нами предположении (граф плоский), противоречит условию. Отсюда заключаем, что полный граф с пятью вершинами не является плоским.▪ [3]

Теорема 11. (Теорема Понтрягина-Куратовского) Граф является плоским тогда и только тогда, когда он не имеет в качестве подграфа полного графа с пятью вершинами. [3]

1.4 Способы представления графов в компьютере

Конструирование структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они так или иначе основаны на тех базовых идеях, которые описаны в этом разделе. [4]

1.4.1 Требования к представлению графов

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(p,q) – объема памяти для каждого представления. Здесь p – число вершин, а q – число ребер. [4]

1.4.2 Матрица смежности

Представление графа с помощью квадратной булевой матрицы M, отражающей смежность вершин, называется матрицей смежности, где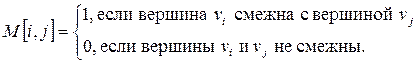

Для матрицы смежности n(p,q) = O(p²).

Замечание

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю (или нижнюю) треугольную матрицу. [4]

1.4.3 Матрица инциденций

Представление графа с помощью матрицы H, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

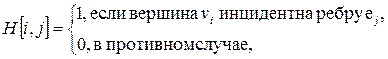
а для орграфа

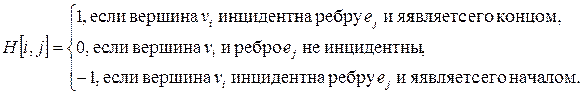
Для матрицы инциденций n(p,q) = O(pq). [4]

1.4.4 Списки смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой

N : record v : 1..p; n :↑ N end record,

называется списком смежности. В случае представления неориентированных графов списками смежности n(p,q) = O(p+2q), а в случае ориентированных графов n(p,q) = O(p+q). [4]

1.4.5 Массив дуг

Представление графа с помощью массива структур

E : array [1..q] of record b,e : 1..p end record,

отражающего список пар смежных вершин, называется массивом ребер (или, для орграфов, массивом дуг). Для массива ребер (или дуг) n(p,q) = O(2q). [4]

1.5 Обзор задач теории графов

Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.

Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.

Далее перечислим некоторые типовые задачи теории графов и их приложения:

- Задача о кратчайшей цепи

замена оборудования

составление расписания движения транспортных средств

размещение пунктов скорой помощи

размещение телефонных станций

- Задача о максимальном потоке

анализ пропускной способности коммуникационной сети

организация движения в динамической сети

оптимальный подбор интенсивностей выполнения работ

синтез двухполюсной сети с заданной структурной надежностью

задача о распределении работ

- Задача об упаковках и покрытиях

оптимизация структуры ПЗУ

размещение диспетчерских пунктов городской транспортной сети

- Раскраска в графах

распределение памяти в ЭВМ

проектирование сетей телевизионного вещания

- Связность графов и сетей

проектирование кратчайшей коммуникационной сети

синтез структурно-надежной сети циркуляционной связи

анализ надежности стохастических сетей связи

- Изоморфизм графов и сетей

структурный синтез линейных избирательных цепей

автоматизация контроля при проектировании БИС

- Изоморфное вхождение и пересечение графов

локализация неисправности с помощью алгоритмов поиска МИПГ

покрытие схемы заданным набором типовых подсхем

- Автоморфизм графов

конструктивное перечисление структурных изомеров для производных органических соединений

синтез тестов цифровых устройств. [2]

Глава 2: Практика

2.1 Общая характеристика задачи

Агентство по грузоперевозкам "Летучий голландец" предоставляет услуги по перевозке грузов по различным маршрутам. Дaнные o маршрутах, выполненных в течение недели, по каждому водителю приведены на таблице 2.1.

Таблица 2.1. Данные о маршрутах

Справочные данные o технических характеристиках автомобилей и протяженности маршрутов представлены на  таблице 2.1.  

Таблица 2.2. Данные о технических характеристиках автомобилей и протяженности маршрутов

1. Построить таблицы по приведенным выше данным.

2.Выполнить расчет количества израсходованного топлива каждым водителем и веса перевезенного груза, данные расчета занести в таблицу.

3. Организовать межтабличные связи для автоматического формирования ведомости расхода топлива за неделю.

4. Сформировать и заполнить ведомость расхода топлива каждым водителем за неделю.

5. Результаты расчета количества израсходованного топлива за неделю представить в графическом виде. [5]

2.2 Описание алгоритма решения задачи

1.        Запустить табличный процессор МS Excel.

2.        Создать книгу с именем “Летучий голландец”.

3.        Лист 1 переименовать в лист с названием Сведения.

4.        На рабочем листе Сведения создать таблицу Сведения о выполненных маршрутах (табл. 2.3).

5.        Заполнить таблицу Сведения о выполненных маршрутах.

6.        Лист 2 переименовать в лист Характеристики.

7.        На рабочем листе Характеристики создать таблицу, в которой будут содержаться технические характеристики автомобилей (табл. 2.4).

8.        Заполнить таблицу со списком Технических характеристик автомобилей.

9.        Лист 3 переименовать в лист Протяженность.

10.   На рабочем листе Протяженность, создать таблицу протяженности рейсов (табл. 2.5).

11.   Заполнить таблицу Протяженность рейсов исходными данными.

12.   Лист 4 переименовать в Ведомость (табл. 2.6).

13.   На рабочем листе Ведомость создать таблицу Ведомость расхода топлива.

14.   Лист 5 переименовать в лист График (табл. 2.7).

15.             На рабочем листе График создать график учета расхода топлива на каждого водителя.

16.             Заполнить графу Израсходовано топливо таблицы “Сведения о выполненных маршрутах” находящейся на листе Сведения следующим образом:

Занести в ячейку H3 формулу: =СУММ(F3*G3/100).

Размножить введенную в ячейку Н3 формулу для остальных ячеек (с Н4 по Н7) данной графы, соответственно меняя строки F3, G3 на соответствующие строкам в столбце Н.

Таким образом, будет выполнен автоматический подсчет израсходованного топлива.

17.             Заполнить графу Вес перевезенного груза таблицы “Сведения о выполненных маршрутах” находящейся на листе Сведения следующим образом:

Занести в ячейку J3 формулу: =СУММ(I3*E3).

Размножить введенную в ячейку J3 формулу для остальных ячеек (с J4 по J7) данной графы, соответственно меняя строки I3, E3 на соответствующие строкам в столбце J.

Таким образом, будет выполнен автоматический подсчет суммы перевезенного груза.

18.             На листе Ведомость заполнить графу Израсходовано топлива следующим образом:

Занести в ячейку Е12 формулу: =СУММ(Сведения!H3).

Размножить введенную в ячейку Е12 формулу для остальных ячеек (с Е12 по Е18) данной графы, соответственно меняя строки формулы с Н3 по Н9.

Таким образом, будет выполнен автоматический подсчет израсходованного топлива.

19.             На листе Ведомость заполнить графу Выполнено рейсов следующим образом:

Занести в ячейку D12 формулу =СУММ(Сведения!E3).

Размножить введенную в ячейку D12 формулу для остальных ячеек (с D13 по D18) данной графы, соответственно меняя строки формулы с Е3 по Е9.

Таким образом, будет выполнен автоматический подсчет количества выполненных рейсов.

20. Пo результатам заполненных параметров в таблице «Ведомость расхода топлива» создать график расхода топлива на листе «график».

Таблица 2.3. Сведения о выполненных маршрутах

Таблица 2.4. Технические характеристики автомобилей

Таблица 2.5.  Протяженность рейсов

Таблица 2.6. Ведомость

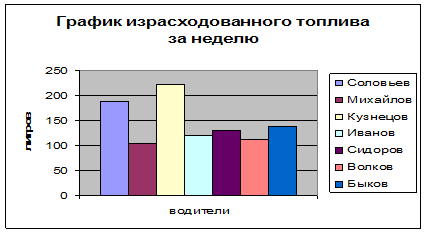
Таблица 2.7. График

 Данная задача решена в приложении Microsoft Office Excel.

Заключение

В работе были рассмотрены задачи из теории графов, которые уже стали классическими. Особенно часто в практическом программировании возникают вопросы о построении кратчайшего остова графа и нахождении максимального паросочетания. Известно также, что задача о нахождении гамильтонова цикла принадлежит к числу NP-полных, т.е. эффективный алгоритм для ее решения не найден. Таким образом, задачи теории графов актуальны, так как могут принести экономию времени и средств на производстве и в быту. Теория графов находит широкое применение в различных областях науки и техники: в частности в информатике.

Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.

Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.

Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.

Список использованной литературы

1.   История возникновения теории графов. Историческая справка. – URL: https://sites.google.com/site/teoriagrafov96/ (дата обращения: 10.11.2016)

2.   Некоторые задачи теории графов. Базовые понятия теории графов. – URL: http://www.bourabai.kz/dm/graph.htm#5 (дата обращения: 15.01.2017)

3.   Основные теоремы теории графов. – URL: http://mirznanii.com/a/312693/teoriya-grafov (дата обращения: 25.12.2016)

4.   Требования к представлению графов. – URL: http://www.studfiles.ru/preview/2619537/page:14/ (дата обращения: 12.02.2017)

5.   Разбор и решение задач. – URL: http://filling-form.ru/turizm/3077/index.html?page=22 (дата обращения: 15.01.2017)

Скачано с www.znanio.ru