
Министерство образования и науки Нижегородской области
Государственное бюджетное профессиональное образовательное учреждение
«Балахнинский технический техникум»
ФОНДЫ ОЦЕНОЧНЫХ СРЕДСТВ
учебной дисциплины общеобразовательного цикла
Математика
программы подготовки специалистов среднего звена по специальностям и профессиям УГС 08.00.00
08.01.26 Мастер по ремонту и обслуживанию инженерных систем
жилищно-коммунального хозяйства
Балахна
2023
Комплект фондов оценочных средств по общеобразовательной дисциплине Математика разработан на основе Федерального государственного образовательного стандарта среднего общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17 мая 2012 г. N 413 (зарегистрирован Министерством юстиции Российской Федерации 7 июня 2012 г., регистрационный N 24480) в последней редакции от 12.08.2022, с учетом примерного фонда оценочных средств по дисциплине Математика авторского коллектива под руководством Лавреновой Екатерины Владимировны, канд. педагогических наук.
Структура и содержание заданий – задания разработаны в соответствии с рабочей программой учебного предмета «Математика».
Результатом освоения учебного предмета являются предусмотренные ФГОС СОО и ФГОС СПО по специальности личностные, метапредметные, предметные результаты, общие компетенции.
Организация-разработчик: Государственное бюджетное профессиональное образовательное учреждение «Балахнинский технический техникум» (ГБПОУ БТТ).
Разработчики:
Грищенкова Ю.С. – преподаватель математики ГБПОУ "Балахнинский технический техникум";
Гаро Н.Ф.- преподаватель математики ГБПОУ "Балахнинский технический техникум";
Рецензенты:
Алексеева Г.А. – методист ГБПОУ «Балахнинский технический техникум»;
Одобрена цикловой методической комиссией УГС
Протокол №__ от «___» ____20__г.
Председатель _______
СОДЕРЖАНИЕ
1. Результаты обучения, регламентированные ФГОС СОО с учетом ФГОС СПО
2. Фонд оценочных средств для входного контроля21
3. Фонд оценочных средств для текущего контроля
4. Фонд оценочных средств для рубежного контроля (по итогам 3.1 – 3.3)
5. Фонд оценочных средств для промежуточной аттестации (экзамен)
1.Результаты обучения, регламентированные ФГОС СОО с учетом ФГОС СПО
Предметные результаты на базовом уровне отражают:
ДРб 01. Владение методами доказательств, алгоритмами решения задач; умение формулировать определения, аксиомы и теоремы, применять их, проводить доказательные рассуждения в ходе решения задач;
ДРб 02. Умение оперировать понятиями: степень числа, логарифм числа; умение выполнять вычисление значений и преобразования выражений со степенями и логарифмами, преобразования дробно-рациональных выражений;
ДРб 03. Умение оперировать понятиями: рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и неравенства, их системы;
ДРб 04. Умение оперировать понятиями: функция, непрерывная функция, производная, первообразная, определенный интеграл; умение находить производные элементарных функций, используя справочные материалы; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций; строить графики многочленов с использованием аппарата математического анализа; применять производную при решении задач на движение; решать практико-ориентированные задачи на наибольшие и наименьшие значения, на нахождение пути, скорости и ускорения;
ДРб 05. Умение оперировать понятиями: рациональная функция, показательная функция, степенная функция, логарифмическая функция, тригонометрические функции, обратные функции; умение строить графики изученных функций, использовать графики при изучении процессов и зависимостей, при решении задач из других учебных предметов и задач из реальной жизни; выражать формулами зависимости между величинами;
ДРб 06. Умение решать текстовые задачи разных типов (в том числе на проценты, доли и части, на движение, работу, стоимость товаров и услуг, налоги, задачи из области управления личными и семейными финансами); составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать полученное решение и оценивать правдоподобность результатов;
ДРб 07. Умение оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение числового набора; умение извлекать, интерпретировать информацию, представленную в таблицах, на диаграммах, графиках, отражающую свойства реальных процессов и явлений; представлять информацию с помощью таблиц и диаграмм; исследовать статистические данные, в том числе с применением графических методов и электронных средств;
ДРб 08. Умение оперировать понятиями: случайный опыт и случайное событие, вероятность случайного события; умение вычислять вероятность с использованием графических методов; применять формулы сложения и умножения вероятностей, комбинаторные факты и формулы при решении задач; оценивать вероятности реальных событий; знакомство со случайными величинами; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях;
ДРб 09. Умение оперировать понятиями: точка, прямая, плоскость, пространство, двугранный угол, скрещивающиеся прямые, параллельность и перпендикулярность прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями; умение использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов окружающего мира;
ДРб 10. Умение оперировать понятиями: многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы, цилиндра, конуса, площадь поверхности пирамиды, призмы, конуса, цилиндра, площадь сферы, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение изображать многогранники и поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств; умение распознавать симметрию в пространстве; умение распознавать правильные многогранники;
ДРб 11. Умение оперировать понятиями: движение в пространстве, подобные фигуры в пространстве; использовать отношение площадей поверхностей и объемов подобных фигур при решении задач;
ДРб 12. Умение вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы;
ДРб 13. Умение оперировать понятиями: прямоугольная система координат, координаты точки, вектор, координаты вектора, скалярное произведение, угол между векторами, сумма векторов, произведение вектора на число; находить с помощью изученных формул координаты середины отрезка, расстояние между двумя точками;
ДРб 14. Умение выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, в искусстве; умение приводить примеры математических открытий российской и мировой математической науки.
ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам
ОК 02. Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности
ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по финансовой грамотности в различных жизненных ситуациях
ОК 04. Эффективно взаимодействовать и работать в коллективе и команде
ОК 05. Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста
ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей, в том числе с учетом гармонизации межнациональных и межрелигиозных отношений, применять стандарты антикоррупционного поведения
ОК 07. Содействовать сохранению окружающей среды, ресурсосбережению, применять знания об изменении климата, принципы бережливого производства, эффективно действовать в чрезвычайных ситуациях.
Профессиональные компетенции 08.01.26 Мастер по ремонту и обслуживанию инженерных систем жилищно-коммунального хозяйства:
ВПД 1 Поддержание рабочего состояния оборудования систем водоснабжения, водоотведения, отопления объектов жилищно-коммунального хозяйства.
ПК 1.1 Осуществлять техническое обслуживание в соответствии с заданием (нарядом) системы
водоснабжения, водоотведения, отопления объектов жилищно-коммунального хозяйства.
ПК 1.2 Проводить ремонт и монтаж отдельных узлов системы водоснабжения, водоотведения.
ПК 1.3 Проводить ремонт и монтаж отдельных узлов системы отопления.
ВПД 2 Поддержание в рабочем состоянии силовых и слаботочных систем зданий и сооружений, системы освещения и осветительных сетей объектов жилищно-коммунального хозяйства.
ПК 2.1 Осуществлять техническое обслуживание силовых и слаботочных систем зданий и сооружений, системы освещения и осветительных сетей объектов жилищно-коммунального хозяйства в соответствии с требованиями нормативно-технической документации.
ПК 2.2 Осуществлять ремонт и монтаж отдельных узлов освещения и осветительных сетей объектов жилищно-коммунального хозяйства в соответствии с требованиями нормативно технической документации.
ПК 2.3 Осуществлять ремонт и монтаж отдельных узлов силовых и слаботочных систем зданий и сооружений в соответствии с требованиями нормативно-технической документации
|
№п/п |
Код
|
Планируемые образовательные результаты обучения |
Наименование оценочного средства |
|
1 |
ОК 01. |
Общие: В части трудового воспитания: 1. готовность к труду, осознание ценности мастерства, трудолюбие; 2. готовность к активной деятельности технологической и социальной направленности, способность инициировать, планировать и самостоятельно выполнять такую деятельность; 3. интерес к различным сферам профессиональной деятельности. Овладение универсальными учебными познавательными действиями: а) базовые логические действия: 1) самостоятельно формулировать и актуализировать проблему, рассматривать ее всесторонне; 2) устанавливать существенный признак или основания для сравнения, классификации и обобщения; 3) определять цели деятельности, задавать параметры и критерии их достижения; 4) выявлять закономерности и противоречия в рассматриваемых явлениях; 5) вносить коррективы в деятельность, оценивать соответствие результатов целям, оценивать риски последствий деятельности; Предметные: - владеть методами доказательств, алгоритмами решения задач; умение формулировать определения, аксиомы и теоремы, применять их, проводить доказательные рассуждения в ходе решения задач; - уметь оперировать понятиями: степень числа, логарифм числа; умение выполнять вычисление значений и преобразования выражений со степенями и логарифмами, преобразования дробно-рациональных выражений; (1) уметь оперировать понятиями: рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и неравенства, их системы, (2)
уметь
оперировать понятиями: функция, непрерывная функция, производная, (3)
уметь
оперировать понятиями: рациональная функция, показательная функция, степенная
функция, логарифмическая функция, тригонометрические функции, обратные
функции; умение строить графики изученных функций, использовать (4) уметь решать текстовые задачи разных типов (в том числе на проценты, доли и части, на движение, работу, стоимость товаров и услуг, налоги, задачи из области управления личными и семейными финансами); составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать полученное решение и оценивать правдоподобность результатов; (5)
уметь
оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее
значения, размах, дисперсия, стандартное отклонение числового набора; (6)
уметь
оперировать понятиями: случайный опыт и случайное событие, вероятность
случайного события; умение вычислять вероятность с использованием графических (7)
уметь
оперировать понятиями: точка, прямая, плоскость, пространство, двугранный
угол, скрещивающиеся прямые, параллельность и перпендикулярность прямых (8) уметь оперировать понятиями: многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, касающаяся сферы, цилиндра, конуса, площадь поверхности пирамиды, призмы, конуса, цилиндра, площадь сферы, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение изображать многогранники и поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств; умение распознавать симметрию в пространстве; умение распознавать правильные многогранники; (9)
уметь
оперировать понятиями: движение в пространстве, подобные фигуры в
пространстве; использовать отношение площадей поверхностей и объемов подобных (10) уметь вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы -уметь
оперировать понятиями: прямоугольная система координат, координаты точки, -
уметь выбирать подходящий изученный метод для решения задачи, распознавать
математические факты и математические модели в природных и общественных
явлениях, в искусстве; умение приводить примеры математических открытий -
уметь оперировать понятиями: определение, аксиома, теорема, следствие, свойство, (11) уметь оперировать понятиями: множество, подмножество, операции надмножествами; умение использовать теоретико- множественный аппарат для описания реальных процессов и явлений при решении задач, в том числе из других учебных предметов; (12) уметь оперировать понятиями: граф, связный граф, дерево, цикл, граф на плоскости; умение задавать и описывать графы различными способами; использовать графы при решении задач; (13) уметь свободно оперировать понятиями: сочетание, перестановка, число сочетаний, число перестановок, бином Ньютона; умение применять комбинаторные факты и рассуждения для решения задач; (14)
уметь
оперировать понятиями: натуральное число, целое число, остаток по модулю,
рациональное число, иррациональное число, множества натуральных, целых,
рациональных, действительных чисел; умение использовать признаки делимости, наименьший
общий делитель и наименьшее общее кратное, алгоритм Евклида (15)
уметь
свободно оперировать понятиями: степень с целым показателем, корень
натуральной степени, степень с рациональным показателем, степень с (16) уметь оперировать понятиями: тождество, тождественное преобразование, уравнение, неравенство, система уравнений и неравенств, равносильность уравнений, неравенств и систем, рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения, неравенства и системы; умение решать уравнения, неравенства и системы с помощью различных приемов; решать уравнения, неравенства и системы с параметром; применять уравнения, неравенства, их системы для решения математических задач и задач из различных областей науки и реальной жизни; (17) уметь свободно оперировать понятиями: график функции, обратная функция, композиция функций, линейная функция, квадратичная функция, степенная функция с целым показателем, тригонометрические функции, обратные тригонометрические функции, показательная и логарифмическая функции; умение строить графики функций, выполнять преобразования графиков функций; умение использовать графики функций для изучения процессов и зависимостей при решении задач из других учебных предметов и из реальной жизни; выражать формулами зависимости между величинами; умение свободно оперировать понятиями: четность функции, периодичность функции, ограниченность функции, монотонность функции, экстремум функции, наибольшее и наименьшее значения функции на промежутке; умение проводить исследование функции; умение использовать свойства и графики функций для решения уравнений, и задач с параметрами; изображать на координатной плоскости множества решений уравнений, неравенств и их систем; (18) уметь свободно оперировать понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия, бесконечно убывающая геометрическая прогрессия; умение задавать последовательности, в том числе с помощью рекуррентных формул; (19)
уметь
оперировать понятиями: непрерывность функции, асимптоты графика функции,
первая и вторая производная функции, геометрический и физический смысл
производной, первообразная, определенный интеграл; умение находить асимптоты
графика функции; умение вычислять производные суммы, произведения, частного и (20) уметь оперировать понятиями: комплексное число, сопряженные комплексные числа, модуль и аргумент комплексного числа, форма записи комплексных чисел (геометрическая, тригонометрическая и алгебраическая); (21) уметь производить арифметические действия с комплексными числами; приводить примеры использования комплексных чисел; (22) уметь свободно оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение для описания числовых данных; умение исследовать статистические данные, в том числе с применением графических методов и электронных средств; графически исследовать совместные наблюдения с помощью диаграмм рассеивания и линейной регрессии; (23) уметь находить вероятности событий с использованием графических методов; применять для решения задач формулы сложения и умножения вероятностей, формулу полной вероятности, формулу Бернулли, комбинаторные факты и формулы; оценивать вероятности реальных событий; умение оперировать понятиями: случайная величина, распределение вероятностей, математическое ожидание, дисперсия и стандартное отклонение случайной величины, функции распределения и плотности равномерного, показательного и нормального распределений; умение использовать свойства изученных распределений для решения задач; знакомство с понятиями: закон больших чисел, методы выборочных исследований; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях; -
уметь свободно оперировать понятиями: точка, прямая, плоскость, пространство,
отрезок, луч, плоский угол, двугранный угол, трехгранный угол,
пересекающиеся, параллельные и скрещивающиеся прямые, перпендикулярность
прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол
между плоскостями; умение использовать при решении задач изученные факты и
теоремы планиметрии; умение оценивать размеры объектов в окружающем мире;
умение оперировать (24)
уметь
свободно оперировать понятиями: движение, параллельный перенос, симметрия на
плоскости и в пространстве, поворот, преобразование подобия, подобные фигуры;
умение распознавать равные и подобные фигуры, в том числе в природе,
искусстве, архитектуре; умение использовать геометрические отношения, (25) уметь моделировать реальные ситуации на языке математики; составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат; строить математические модели с помощью геометрических понятий и величин, решать связанные с ними практические задачи; составлять вероятностную модель и интерпретировать полученный результат; решать прикладные задачи экономического и физического характера; умение выбирать подходящий метод для решения задачи; понимание значимости математики в изучении природных и общественных процессов и явлений; умение распознавать проявление законов математики в искусстве, умение приводить примеры математических открытий российской и мировой математической науки |
экзаменационных |
|
2 |
OK 02 |
Общие: В
области ценности научного познания: - совершенствование языковой и читательской культуры как средства взаимодействия между людьми и познания мира; - осознание ценности научной деятельности, готовность осуществлять проектную и исследовательскую деятельность индивидуально и в группе; Овладение универсальными учебными познавательными действиями: в) работа с информацией: 1. владеть навыками получения информации из источников разных типов, самостоятельно осуществлять поиск, анализ, систематизацию и интерпретацию информации различных видов и форм представления; - создавать тексты в различных форматах с учетом назначения информации и целевой аудитории, выбирая оптимальную форму представления и визуализации; 2. оценивать
достоверность, легитимность информации, ее соответствие правовым и 3. использовать средства информационных и коммуникационных технологий в решении когнитивных, коммуникативных и организационных задач с соблюдением требований эргономики, техники безопасности, гигиены, ресурсосбережения Предметные: - уметь оперировать понятиями: рациональная функция, показательная функция, степенная функция, логарифмическая функция, тригонометрические функции, обратные функции; умение строить графики изученных функций, использовать графики при изучении процессов и зависимостей, при решении задач из других учебных предметов и задач из реальной жизни; выражать формулами зависимости между величинами; - уметь оперировать понятиями: тождество, тождественное преобразование, уравнение, неравенство, система уравнений и неравенств, равносильность уравнений, неравенств и систем, рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и системы; уметь решать уравнения, неравенства и системы с помощью различных приемов; решать уравнения, неравенства и системы с параметром; применять уравнения, неравенства, их системы для решения математических задач и задач из различных областей науки и реальной жизни; - уметь свободно оперировать понятиями: движение, параллельный перенос, симметрия на плоскости и в пространстве, поворот, преобразование подобия, подобные фигуры; уметь распознавать равные и подобные фигуры, в том числе в природе, искусстве, архитектуре; - уметь использовать геометрические отношения, находить геометрические отношения, находить геометрические величины (длина, угол, площадь, объем) при решении задач из других учебных предметов и из реальной жизни |
|
|
3 |
ОК 03 |
Общие: В области духовно-нравственного
воспитания: - способность оценивать ситуацию и принимать осознанные решения, ориентируясь на морально-нравственные нормы и ценности; - осознание личного вклада в построение устойчивого будущего; - ответственное отношение к своим родителям и(или) другим членам семьи, созданию семьи на основе осознанного принятия ценностей семейной жизни в соответствии с традициями народов России; Овладение универсальными регулятивными действиями: а) самоорганизация: - самостоятельно осуществлять познавательную деятельность, выявлять проблемы, ставить и формулировать собственные задачи в образовательной деятельности и жизненных ситуациях; - самостоятельно составлять план решения самоконтроль: - использовать приемы рефлексии для оценки ситуации, выбора верного решения; - уметь оценивать риски и своевременно принимать решения по их снижению; 1) эмоциональный интеллект, предполагающий сформированность: внутренней мотивации, включающей стремление к достижению цели и успеху, оптимизм, инициативность, умение действовать, исходя из своих возможностей; - эмпатии, включающей способность понимать эмоциональное состояние других, учитывать его при осуществлении коммуникации, способность к сочувствию и сопереживанию; -
социальных навыков, включающих способность выстраивать отношения с другими Предметные: - уметь оперировать понятиями: рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и неравенства, их системы; -
уметь оперировать понятиями: многогранник, сечение многогранника, куб,
параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр,
конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы,
цилиндра, конуса, площадь поверхности призмы, конуса, цилиндра, площадь
сферы, объем куба, - уметь оперировать понятиями: прямоугольная система координат, координаты точки, вектор, координаты вектора, скалярное произведение, угол между векторами, сумма векторов, произведение вектора на число; находить с помощью изученных формул координаты середины отрезка |
работ |
|
4 |
ОК04 |
Общие: готовность к саморазвитию, самостоятельности и самоопределению; - овладение навыками учебно - исследовательской, проектной и социальной деятельности; Овладение универсальными коммуникативными действиями: 3. совместная деятельность: - понимать и использовать преимущества командной и индивидуальной работы; - принимать цели совместной деятельности, организовывать и координировать действия по ее достижению: составлять план действий, распределять
роли с учетом мнений участников - координировать и выполнять работу в условиях реального, виртуального и комбинированного взаимодействия; -
осуществлять позитивное стратегическое поведение в различных ситуациях,
проявлять творчество и воображение, быть инициативным. г) принятие себя и других людей: 1) принимать мотивы и аргументы других людей при анализе результатов деятельности; 2) признавать свое право и право других людей на ошибки; 3) развивать способность понимать мир с позиции другого человека Предметные: - уметь оперировать понятиями: случайный опыт и случайное событие, вероятность случайного события; уметь вычислять вероятность с использованием графических методов; - применять формулы сложения и умножения вероятностей, комбинаторные факты и формулы при решении задач; оценивать вероятности реальных событий; знакомство со случайными величинами; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях; - уметь свободно оперировать понятиями: степень с целым показателем, корень натуральной степени, степень с рациональным показателем, степень с действительным (вещественным) показателем, логарифм числа, синус, косинус и тангенс произвольного числа; - уметь свободно оперировать понятиями: график функции, обратная функция, композиция функций, линейная функция, квадратичная функция, степенная функция с целым показателем, тригонометрические функции, обратные тригонометрические функции, показательная и логарифмическая функции; уметь строить графики функций, выполнять преобразования графиков функций; - уметь использовать графики функций для изучения процессов и зависимостей при решении задач из других учебных предметов и из реальной жизни; выражать формулами зависимости между величинами; свободно оперировать понятиями: четность функции, периодичность функции, ограниченность функции, монотонность функции, экстремум функции, наибольшее и наименьшее значения функции на промежутке; уметь проводить исследование функции; - уметь использовать свойства и графики функций для решения уравнений, неравенств и задач с параметрами; изображать на координатной плоскости множества решений уравнений, неравенств и их систем
|
работ |
|
5 |
ОК05 |
Общие: В области эстетического воспитания: 1) эстетическое отношение к миру, включая эстетику быта, научного и технического творчества, спорта, труда и общественных отношений; 2) способность воспринимать различные виды искусства, традиции и творчество своего и других народов, ощущать эмоциональное воздействие искусства 3) убежденность в
значимости для личности и общества отечественного и мирового искусства, -
готовность к самовыражению в разных видах искусства, стремление проявлять
качества - Овладение универсальными коммуникативными действиями: а) общение: - осуществлять коммуникации во всех сферах жизни; -
распознавать невербальные средства общения, понимать значение социальных
знаков, - развернуто и логично излагать свою точку зрения с использованием языковых средств Предметные: -
уметь
оперировать понятиями: среднее арифметическое, медиана, наибольшее и
наименьшее значения, размах, дисперсия, стандартное отклонение числового
набора; умение извлекать, интерпретировать информацию, представленную в
таблицах, на диаграммах, графиках, 4) уметь оперировать понятиями: точка, прямая, плоскость, пространство, двугранный угол, скрещивающиеся прямые, параллельность и перпендикулярность прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями; - уметь использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов окружающего мира |
работ |
|
6 |
ОК06 |
Общие: знание обучающимися российской гражданской идентичности; - целенаправленное развитие внутренней позиции личности на основе духовно-нравственных ценностей народов Российской Федерации, исторических и национально-культурных традиций, формирование системы значимых ценностно -смысловых установок антикоррупционного мировоззрения, правосознания, экологической культуры, способности ставить цели и строить жизненные планы в части гражданского воспитания: - осознание своих конституционных прав и обязанностей, уважение закона и правопорядка; - принятие традиционных национальных, общечеловеческих гуманистических и демократических ценностей; - готовность противостоять идеологии экстремизма, национализма, ксенофобии, дискриминации по социальным, религиозным, расовым, национальным признакам; - готовность вести совместную деятельность в интересах гражданского общества, участвовать в самоуправлении в общеобразовательной организации и детско-юношеских организациях; -
умение взаимодействовать с социальными институтами в соответствии с их
функциями и - готовность к гуманитарной и волонтерской деятельности; патриотического воспитания: ценностное отношение к государственным символам, историческому и природному наследию, памятникам, традициям народов России, достижениям России в науке, искусстве, спорте, технологиях и труде; -
идейная убежденность, готовность к служению и защите Отечества,
ответственность за его - способность их использования в познавательной и социальной практике, готовность к самостоятельному планированию и осуществлению учебной деятельности, организации учебного сотрудничества с работниками и сверстниками, к участию в построении индивидуальной образовательной траектории; - овладение навыками учебно-исследовательской, проектной и социальной деятельности Предметные: - уметь оперировать понятиями: прямоугольная система координат, координаты точки, вектор, координаты вектора, скалярное произведение, угол между векторами, сумма векторов, произведение вектора на число; находить с помощью изученных формул координаты середины отрезка, расстояние между двумя точками; -уметь выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, умение приводить примеры математических открытий российской и мировой математической науки. -
уметь оперировать понятиями: случайный опыт и случайное событие, вероятность
случайного события; уметь вычислять вероятность с использованием графических
методов; применять формулы сложения и умножения вероятностей, комбинаторные
факты и формулы при решении задач; оценивать вероятности реальных событий;
знакомство со случайными величинами; |
работ |
|
7 |
ОК07 |
Общие: не принимать действия, приносящие вред окружающей среде; -
уметь прогнозировать неблагоприятные экологические последствия
предпринимаемых - расширить опыт деятельности экологической направленности; - разрабатывать план решения проблемы с учетом анализа имеющихся материальных и нематериальных ресурсов; 1.
осуществлять
целенаправленный поиск переноса средств и способов действия в 2. уметь переносить знания в познавательную и практическую области жизнедеятельности; 3. предлагать новые проекты, оценивать идеи с позиции новизны, оригинальности, практической значимости; -
давать оценку новым ситуациям, вносить коррективы в деятельность, оценивать Предметные: -
уметь оперировать понятиями: функция, непрерывная функция, производная,
первообразная, определенный интеграл; 1. уметь оперировать понятиями: движение в пространстве, подобные фигуры в пространстве; использовать отношение площадей поверхностей и объемов подобных фигур при решении задач; 2. уметь вычислять
геометрические величины (длина, угол, площадь, объем, площадь поверхности),
используя изученные формулы и методы |
работ |
2.Фонд оценочных средств для входного контроля
Входная контрольная работа по математике составлена на основе Федерального государственного образовательного стандарта среднего общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17 мая 2012 г. N 413 (зарегистрирован Министерством юстиции Российской Федерации 7 июня 2012 г., регистрационный N 24480) в последней редакции от 12.08.2022, в соответствии с действующей Рабочей программой по математике, рассмотренной и одобренной на заседании цикловой методической комиссии общеобразовательных дисциплин протокол №11 от 14.06.2023 г. и утверждена приказом ГБПОУ БТТ от 15.06.2023 г. №369 и предназначена для проведения входного контроля по математике для студентов 1 курса по профессиям и специальностям для УГПС 08.00.00:
08.01.26 Мастер по ремонту и обслуживанию инженерных систем
жилищно-коммунального хозяйства
Цель: установление фактического уровня теоретических знаний обучающихся по математике обязательного компонента учебного плана, их практических умений и навыков; установление соответствия уровня ЗУН обучающихся требованиям государственного образовательного стандарта общего образования.
Контрольная работа по математике состоит из 2 вариантов. Каждый вариант включает 14 тестовых заданий по разделам: алгебра, геометрия, реальная математика. Материалы для составления контрольной работы взяты из банка заданий для подготовки учащихся к сдаче ОГЭ.
Ответом на каждое задание служит целое число или десятичная дробь.
На выполнение контрольной работы отводится 1 час 30 минут.
По результатам работы каждому учащемуся выставляется оценка по математике.
Каждое верно выполненное задание оценивается 1 баллом.
13-14 баллов выставляется оценка «5»
8 – 12 баллов выставляется оценка «4»
6-7 баллов выставляется оценка «3»
Менее 6 баллов выставляется оценка «2»
ВАРИАНТ I
Задание 1:
Найдите
значение выражения ![]()
Задание 2:
Известно,
что a и b — положительные числа
и ![]() Сравните
Сравните ![]() и
и ![]()
В ответе укажите номер правильного варианта.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) сравнить невозможно
4) сравнить невозможно
Задание 3:
Найдите значение выражения
![]()
при ![]()
Задание 4:
Решите систему уравнений
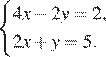
В ответ запишите х + у.
Задание 5:
Из каждых 1000 электрических лампочек 5 бракованных. Какова вероятность купить исправную лампочку?
Задание 6:
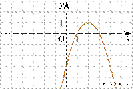
На рисунке изображён график функции
![]()
Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
|
1) [0; 3] 2) [− 1; 1] 3) [2; 4] 4) [1; 4] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
|
|
|
Задание 7:
Площадь
параллелограмма ![]() можно вычислить
по формуле
можно вычислить
по формуле ![]() где
где ![]() — стороны параллелограмма (в метрах). Пользуясь этой
формулой, найдите площадь параллелограмма, если его стороны 10 м и
12 м и
— стороны параллелограмма (в метрах). Пользуясь этой
формулой, найдите площадь параллелограмма, если его стороны 10 м и
12 м и ![]()
Задание 8:
Решите систему неравенств
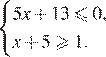
Задание 9:
На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
Задание 10:

Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
Задание 11:
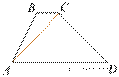
В трапеции ABCD известно, что AD = 4, BC = 1, а её площадь равна 35. Найдите площадь треугольника ABC.
Задание 12:

На
рисунке с размером клетки 1×1 изображен параллелограмм ABCD.
Используя рисунок, найдите ![]()
Задание 13:
Решите
неравенство ![]()
Задание 14:
Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Задание 15:
Постройте
график функции ![]() и
найдите все значения k, при которых прямая
и
найдите все значения k, при которых прямая ![]() имеет с графиком данной функции ровно одну общую точку.
имеет с графиком данной функции ровно одну общую точку.
ВАРИАНТ II
Задание 1:
Найдите значение выражения ![]()
Задание 2:
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
Задание 3:
Упростите выражение
![]()
и найдите его значение при ![]()
В ответе запишите найденное значение.
Задание 4:
Решите уравнение ![]()
Задание 5:
Найдите значение k по графику
функции ![]() изображенному
на рисунке.
изображенному
на рисунке.
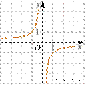
Задание 6:
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.
Задание 7:
На каком рисунке изображено множество решений
неравенства ![]()
В ответе укажите номер правильного варианта.
|
1)
|
2)
|
|
3)
|
4)
|
Задание 8:

Сторона равностороннего треугольника равна ![]() Найдите
медиану этого треугольника.
Найдите
медиану этого треугольника.
Задание 9:
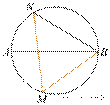
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 38°. Найдите угол NMB. Ответ дайте в градусах.
Задание 10:

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Задание 11:
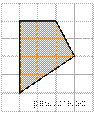
Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.
Задание 12:
Решите уравнение ![]()
Задание 13:
Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Задание 14:
Постройте график функции ![]() и
определите, при каких значениях k построенный график не будет
иметь общих точек с прямой
и
определите, при каких значениях k построенный график не будет
иметь общих точек с прямой ![]()
Ключ: Вариант I
Задание 1:
Найдите
значение выражения ![]()
Решение. Умножим числитель и знаменатель на 100:
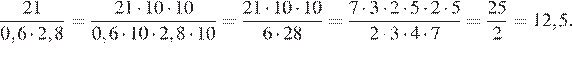
Ответ: 12,5.
Задание 2:
Известно,
что a и b — положительные числа
и ![]() Сравните
Сравните ![]() и
и ![]()
В ответе укажите номер правильного варианта.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4) сравнить невозможно
4) сравнить невозможно
Решение. Числа a и b положительные, ![]() поэтому
поэтому ![]()
Задание 3:
Найдите
значение выражения ![]() при
при ![]()
Решение. Упростим выражением
![]()
Подставим
значения ![]() :
:
![]()
Ответ: -28,8
Задание 4:
Решите
систему уравнений 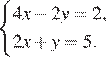 В
ответ запишите х + у.
В
ответ запишите х + у.
Решение. Разделим обе части первого уравнения на 2 и решим систему методом подстановки:
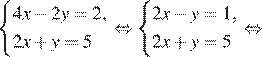
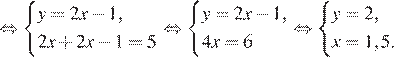
Искомая сумма равна 3,5.
Ответ: 3,5.
Примечание.
Систему можно было бы решить методом алгебраического сложения:
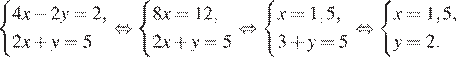
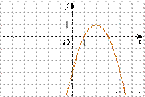
Задание 5:
На
рисунке изображён график функции ![]() Установите соответствие
между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
Установите соответствие
между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
|
УТВЕРЖДЕНИЯ |
|
ПРОМЕЖУТКИ |
|
А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
|
1) [0; 3] 2) [− 1; 1] 3) [2; 4] 4) [1; 4] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
|
|
|
Решение. Заметим, что функция возрастает на промежутке (−∞; 2] и убывает на промежутке [2; +∞). Таким образом, она возрастает на промежутке [− 1; 1] и убывает на промежутке [2; 4].
Ответ: 23.
Примечание.
Заметим, что если функция непрерывна на промежутке [a; b] и возрастает (убывает) на промежутке (a; b), то она возрастает (убывает) на промежутке [a; b]. Таким образом, утверждение, что данная функция убывает на промежутке [2; 4], является верным, хотя точка 2 является точкой максимума функции.
Задание 6:
Площадь
параллелограмма ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где ![]() — стороны параллелограмма (в метрах). Пользуясь этой
формулой, найдите площадь параллелограмма, если его стороны 10 м и
12 м и
— стороны параллелограмма (в метрах). Пользуясь этой
формулой, найдите площадь параллелограмма, если его стороны 10 м и
12 м и ![]()
Решение. Подставим
в формулу известные значения величин: ![]()
Ответ: 60.
Задание 7:
Решите систему неравенств
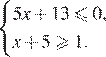
На каком рисунке изображено множество её решений?
В ответе укажите номер правильного варианта.
|
1)
|
2)
|
|
3)
|
4)
|
Решение. Решим систему:
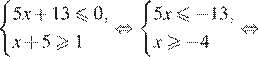
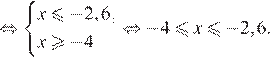
Решением системы является отрезок, изображённый под номером 2.
Правильный ответ указан под номером 2.
Задание 8:
На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.

Решение.
Треугольник CDE —
равнобедренный, следовательно, ![]()
Тогда угол CDE равен
![]()
![]()
Угол ADE — развёрнутый, он состоит из двух углов: ADC и CDE. Значит, больший угол ADC параллелограмма ABCD будет равен
![]()
Ответ: ![]()
Задание 9:

Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
Решение. Дуги
окружности относятся как 9:11, что в сумме дает 20 частей. Поэтому длина
меньшей дуги составляет ![]() от всей
окружности, тем самым, она равна
от всей
окружности, тем самым, она равна ![]() Так
как угол AOB — центральный, то он равен той дуге на
которую он опирается. Таким образом,
Так
как угол AOB — центральный, то он равен той дуге на
которую он опирается. Таким образом, ![]()
Ответ: 162.
Задание 10:
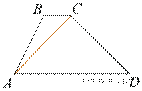
В трапеции ABCD известно, что AD = 4, BC = 1, а её площадь равна 35. Найдите площадь треугольника ABC.
Решение. Пусть
длина высоты трапеции равна ![]() Площадь
трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь
трапеции можно найти как произведение полусуммы оснований на высоту:
![]()
Высота
трапеции также является высотой треугольника ![]() Найдём
площадь треугольника ABC как полупроизведение основания на
высоту:
Найдём
площадь треугольника ABC как полупроизведение основания на
высоту:
![]() ,
,
Ответ 7 кв.ед.
Задание 11:

На
рисунке с размером клетки 1×1 изображен параллелограмм ABCD.
Используя рисунок, найдите ![]()
Решение. Синус
угла в прямоугольном треугольнике — отношение противолежащего
катета к гипотенузе. Треугольник BDC — прямоугольный,
поэтому ![]()
Вычислим по теореме Пифагора длину гипотенузы CD:
![]()
Тогда
![]()
Ответ: 0,6.
Задание 12:
Решите
неравенство ![]()
Решение. Перенесём
две части неравенства в одну часть и раскроем скобки: ![]() приравняем левую часть к
нулю и найдём корни. Отсюда
приравняем левую часть к
нулю и найдём корни. Отсюда ![]() и
и ![]() Расставив корни на
координатной прямой, определим знаки неравенства, отсюда:
Расставив корни на
координатной прямой, определим знаки неравенства, отсюда: ![]()
Ответ: ![]()
Задание 13:
Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Решение. Пусть x км/ч —
собственная скорость баржи, тогда ![]() км/ч —
скорость баржи против течения, а
км/ч —
скорость баржи против течения, а ![]() —
скорость баржи по течению. По течению баржа двигалась
—
скорость баржи по течению. По течению баржа двигалась ![]() часов, а
против течения
часов, а
против течения ![]() часов.
Баржа затратила на весь путь 5 часов, составим уравнение:
часов.
Баржа затратила на весь путь 5 часов, составим уравнение:
![]()
![]()
![]()
Корень −1 не подходит по условию задачи, следовательно, скорость баржи равна 15 км/ч.
Ответ: 15
Задание 14:
Постройте
график функции ![]() и
найдите все значения k, при которых прямая
и
найдите все значения k, при которых прямая ![]() имеет с графиком данной функции ровно одну общую точку.
имеет с графиком данной функции ровно одну общую точку.
Решение. Раскроем модули:
![]()
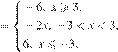
График изображён на рисунке.

Прямая ![]() имеет с графиком данной
функции ровно одну общую точку при
имеет с графиком данной
функции ровно одну общую точку при ![]()
Ответ: ![]()
Примечание.
Заметим, что точки, в которых подмодульное выражение равно 0, могут быть отнесены как к промежутку, на которым модуль раскрывается со знаком «плюс», так и к промежутку, на котором модуль раскрывается со знаком «минус». В частности, после преобразований функцию можно было задать следующим образом:
![]()
КЛЮЧ: ВАРИАНТ II:
Задание1:
Найдите
значение выражения ![]()
Ответ: 8
Задание 2:
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.
![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ: 4
Задание 3:
Упростите
выражение ![]() и
найдите его значение при
и
найдите его значение при ![]() В ответе запишите
найденное значение.
В ответе запишите
найденное значение.
Ответ: 4
Задание 4:
Решите
уравнение ![]()
Ответ: 4
Задание 5:
Найдите
значение k по графику функции ![]() изображенному
на рисунке.
изображенному
на рисунке.
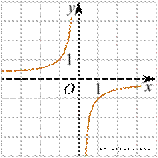
Ответ: -1
Задание 6:
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.
Ответ: 6
Задание 7:
На
каком рисунке изображено множество решений неравенства ![]()
В ответе укажите номер правильного варианта.
|
1)
|
2)
|
|
|
|
3)
|
4)
|
||
Ответ: 1
Задание 8:
В первый день больной заражает четырёх человек, каждый из которых на следующий день заражает новых четырех и так далее. На второй день больной изолируется и больше уже никого не заражает. Болезнь длится 14 дней. В первый день месяца в город N приехал заболевший гражданин К, и в этот же день он заразил четырех человек. В какой день станет 1365 заболевших? (В ответе укажите только число.)
Ответ: 5
Задание 9:

Сторона
равностороннего треугольника равна ![]() Найдите
медиану этого треугольника.
Найдите
медиану этого треугольника.
Ответ: 24
Задание 10:
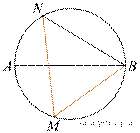 На окружности по разные стороны от
диаметра AB взяты точки M и N.
Известно, что ∠NBA = 38°.
Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от
диаметра AB взяты точки M и N.
Известно, что ∠NBA = 38°.
Найдите угол NMB. Ответ дайте в градусах.
Ответ: 52
Задание 11:

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Ответ: 18
Задание 12:
 Площадь одной клетки равна 1. Найдите
площадь закрашенной фигуры.
Площадь одной клетки равна 1. Найдите
площадь закрашенной фигуры.
Ответ: 8
Решите
уравнение ![]()
Ответ: ![]()
Задание 13:
Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Ответ: 10.
Задание 14:
Постройте
график функции ![]() и
определите, при каких значениях k построенный график не будет
иметь общих точек с прямой
и
определите, при каких значениях k построенный график не будет
иметь общих точек с прямой ![]()
Ответ: ![]()
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 5, ДРб 6, ДРб 9, ДРб 12, ДРб 14.
ОК 01, ОК 02, ОК 05, ОК 06.
ПК 1.1. ПК 1.2
Формы контроля и оценивания элементов учебного предмета
В результате текущей аттестации по предмету осуществляется комплексная проверка личностных, метапредметных, предметных результатов освоения, а также динамика формирования общих компетенций:
|
Раздел / тема учебного предмета |
Проверяемые результаты освоения, ОК |
Форма текущего контроля и оценивания |
|
Раздел 1.
Повторение основной школы Раздел 4. Основы
Раздел 6.
Производная Раздел 7. Раздел 8. Раздел 14.
Уравнения и
|
ОК 01. Выбирать способы решения задач
профессиональной деятельности применительно ОК 02. Использовать современные средства
поиска, анализа и интерпретации информации, и информационные технологии для
выполнения OK 03. Планировать и
реализовывать собственное ОК 04. Эффективно взаимодействовать и OK 05. Осуществлять
устную и письменную ОК Об. Проявлять гражданско-
патриотическую позицию, демонстрировать осознанное поведение на ОК 07. Содействовать сохранению
окружающей |
Письменный опрос Устный опрос Самостоятельная работа Представление результатов практических работ Защита
творческих работ Выполнение
|
|
Раздел 2 Прямые
и пространстве |
ОК 01. Выбирать способы решения задач
профессиональной деятельности применительно OK 03. Планировать и
реализовывать собственное ОК 04. Эффективно взаимодействовать и ОК 07. Содействовать сохранению
окружающей |
|
|
Раздел 3.
Координаты и |
ОК 02. Использовать современные средства
поиска, анализа и интерпретации информации, и информационные технологии для
выполнения OK 03. Планировать и
реализовывать собственное ОК 04. Эффективно взаимодействовать и ОК 07. Содействовать сохранению
окружающей |
Выполнение
|
|
Раздел 5. Комплексные числа Раздел 9. Степени и корни. Степенная функция Раздел10. Показательная функция Раздел 11. Логарифмы. Логарифмическая функция Раздел 12. Раздел 13.
Элементы |
ОК 01. Выбирать способы решения задач
профессиональной деятельности применительно ОК 02. Использовать современные средства
поиска, анализа и интерпретации информации, и информационные технологии для
выполнения OK 03. Планировать и
реализовывать собственное ОК 04. Эффективно взаимодействовать и OK 05. Осуществлять
устную и письменную ОК 07. Содействовать сохранению
окружающей |
Устный опрос Устный опрос Письменный опрос Самостоятельная Выполнение |
Оценка освоения учебного предмета
Предметом оценки служат результаты освоения, направленные на формирование ОК, предусмотренные ФГОС СОО и с ФГОС СПО по специальности.
Перечень контрольных заданий и иных материалов текущего контроля, необходимых для оценки результатов освоения, ОК1, ОК2, ОК3, ОК4, ОК5, ОК6, ОК7:
Типовые задания для оценки результатов освоения, ОК:
Письменный опрос ОК01, ОК02, ОК03, ОК04, ОК05, ОК06, ОК07
ü Формулы сокращенного умножения
ü Основные тригонометрические тождества
ü Показательная функция, ее график и свойствах
ü Логарифмическая функция ее график и свойства
ü Формулы и правила дифференцирования
ü Формулы интегрирования
ü Свойства неопределенного и определенного интегралов
Реферат ОК01, ОК02, ОК03,ОК04, ОК05, ОК06, ОК07
ü Значение математики в моей будущей профессии
ü Симметрия в природе, архитектуре, технике, быту
ü Логарифмическая спираль в природе
Практические работы ОК01, ОК02, ОК03,ОК04, ОК05, ОК06, ОК07
Устный опрос ОК01, ОК02, ОК03,ОК04, ОК05, ОК06, ОК07
Самостоятельные работы ОК01, ОК02, ОК03,ОК04, ОК05, ОК06, ОК07
Контрольные работы ОК01, ОК02, ОК03,ОК04, ОК05, ОК06, ОК07:
Текущий контроль проводятся во время аудиторных занятий по математике в соответствии с учебным планом и рабочей программы ОД «Математика» по всем разделам программы. Текущий контроль состоит из двух частей: теоретической и практической. При этом обучающиеся получают две отметки.
Теоретическая часть проходит в форме устных ответов: обучающиеся вытягивают пять карточек с вопросами, дают полный ответ (со списком вопросов обучающиеся знакомятся в начале изучения раздела).
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Количество верных ответов на теоретические вопросы
|
|
«3» (удов.) |
3 |
|
«4» (хорошо) |
4 |
|
«5» (отлично) |
5 |
Задания практической части (контрольные работы) частично взяты из открытого банка ЕГЭ и ВПР по математике.
На выполнение контрольной работы по математике дается 1 академический час (45 минут).
Контрольная работа состоит их 2-х частей. В первой части предлагается выполнить 4 задания – выбрать правильный ответ из четырех предложенных. Во второй части предлагается выполнить 6 заданий – оформить ход решения и записать полученный ответ.
За правильное выполнение любого задания первой части обучающийся получает один балла. Правильное выполнение заданий второй части оценивается 2 баллами или 1 баллом за частичное решение.
Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«3» (удов.) |
8-10 |
|
«4» (хорошо) |
11-13 |
|
«5» (отлично) |
14-16 |
Прямые и плоскости, координаты и векторы в пространстве
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 9, ДРб 11, ДРб 12, ДРб 13, ДРб 14.
ОК 01, ОК 03, ОК 05, ОК 07.
ПК 1.2.
Теоретические вопросы:
1. Сформулируйте теорему Пифагора.
2. Перечислите основные фигуры в пространстве.
3. Перечислите способы задания плоскости.
4. Продолжите теорему: «Если одна из двух параллельных прямых перпендикулярна плоскости, то…».
5. Продолжите теорему: «Если две параллельные плоскости пересекаются третьей, то…».
6. Сформулируйте определение двугранного угла.
7. Раскройте понятие «угол между прямыми».
8. Перечислите взаимное расположение двух прямых в пространстве
9. Какие прямые называются параллельными в пространстве?
10. Какие прямые называются скрещивающимися в пространстве?
11. Какие прямые называются перпендикулярными в пространстве?
12. Перечислите взаимное расположение прямой и плоскости в пространстве.
13. Раскройте понятие «угол между прямой и плоскостью».
14. Раскройте понятие «параллельность прямой и плоскости».
15. Раскройте понятие «перпендикулярность прямой и плоскости».
16. Перечислите взаимное расположение двух плоскостей в пространстве.
17. Раскройте понятие «угол между плоскостями».
18. Раскройте понятие «параллельность плоскостей».
19. Раскройте понятие «перпендикулярность плоскостей».
20. Как найти расстояние от точки до прямой?
21. Как найти расстояние между прямыми?
22. Как найти расстояние между плоскостями?
23. Продолжите определение: «Перпендикуляр – это…».
24. Продолжите определение: «Наклонная – это…».
25. Продолжите определение: «Проекция наклонной – это…».
26. Перечислите свойства параллельного проектирования.
27. Из чего состоит прямоугольная система координат в пространстве?
28. Если точка лежит в плоскости ху, какая координата у нее нулевая?
29. Приведите пример координат точки А, которая лежит на оси z.
30. Раскройте понятие «вектор».
31. Какие векторы называются коллинеарными?
32. Какие векторы называются перпендикулярными?
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1.
(1
балл) Расшифруйте
краткую запись: a∈![]() .
.
А)
точка a принадлежит
плоскости![]() ; Б) точка a принадлежит
прямой
; Б) точка a принадлежит
прямой![]() ; В) прямая a принадлежит
плоскости
; В) прямая a принадлежит
плоскости![]() Г) прямая a пересекает
плоскост
Г) прямая a пересекает
плоскост![]() .
.
2. (1 балл) Прямые АВ и СД скрещиваются. Какое расположение имеют прямые АС и ВД?
А) параллельные; Б) перпендикулярные; В) скрещиваются; Г) пересекаются.
3. (1 балл) Какие из векторов а(1,2,-3), с(3,6,-6), в(2,4,-6) коллинеарные?
А) а, в; Б) с, в; В) а, с; Г) коллинеарных векторов нет.
4. (1 балл) Даны точки А(2,0,5), В(2,4,-2) С(-2,6,3). Серединой какого отрезка является точка М(0,3,4)?
А) АВ; Б) ВС; В) АС; Г) СВ.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5. (2 балла) Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если АА1=6,8см, ВВ1=7,4см.
6. (2 балла) Прямые АС, АВ и АД попарно перпендикулярны. Найдите отрезок СД, если АВ=5 см, ВС=13 см, АД=9 см.
7. (2 балла) (2 балла) Даны векторы а(-6,0,8) , в(-3,2,-6). Найдите скалярное произведение векторов.
8.
(2 балла) Начертить куб АВСДА1В1С1Д1.
Построить точку К![]() АВ, точку М
АВ, точку М![]() ДД1С, отрезок РЕ
ДД1С, отрезок РЕ![]() А1В1С1.
А1В1С1.
9.
(2 балла) При каких значениях п векторы![]() (4,п,2),
(4,п,2), ![]() (1,2,п) перпендикулярны?
(1,2,п) перпендикулярны?
10. (2 балла) Оформите лист бумаги А4 вертикальными, горизонтальными, наклонными линиями, используя разные цветовые оттенки.
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
В |
В |
А |
В |
7,1 |
15 |
-30 |
- |
-1 |
- |
Основы тригонометрии. Тригонометрические функции
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 3, ДРб 5, ДРб 14.
ОК 01, ОК 02, ОК 03.
Теоретические вопросы:
1. Чему равен угол в один радиан?
2. В каких четвертях тригонометрического круга функция у=sinх принимает положительные значения?
3. В каких четвертях тригонометрического круга функция у= cosx принимает отрицательные значения?
4. Продолжите определение: «Синус острого угла – это…».
5. Продолжите определение: «Косинус острого угла – это…».
6. Продолжите определение: «Тангенс острого угла – это…».
7. Сформулируйте основное тригонометрическое тождество.
8. Чему равно произведение tgx*ctgx?
9. Чему равен sin(2x)? Сформулируйте правило вычисления.
10. Чему равен cos(2x)? Сформулируйте правило вычисления.
11. Перечислите тригонометрические функции, укажите их периоды.
12. Чему равен период функции y=cos(4x)?
13. ему равен период функции y=cos(x/4)?
14. Определите область значения функции y=3cos(5x)?
15. Перечислите способы решения тригонометрических уравнений.
16. Раскройте алгоритм решения однородных тригонометрических уравнений первого порядка.
17. Раскройте алгоритм решения однородных тригонометрических уравнений второго порядка.
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1
балл) В
![]() АВС cosС=
АВС cosС=![]() . Какая из сторон является гипотенузой
. Какая из сторон является гипотенузой ![]() АВС?
АВС?
А)
АВ; Б) АС; В) ВС![]() Г) СВ.
Г) СВ.
2. (1 балл) Углом какой четверти является угол α=410°?
А) I; Б) II; В) III; Г) IV.
3. (1 балл) Какие из функций являются чётными?
А) у=sin х; Б) у=cos х; В) у=tg х; Г) у=сtg х.
4. (1 балл) Период функции у=sinх?
А) π/2; Б) 2π; В) 4π; Г) π.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5. (2 балла) Вычислите: sin![]() + cos
+ cos![]() .
.
6. (2 балла) Найдите значение
выражения 4аrсcos![]() - 4аrсsin
- 4аrсsin![]()
7.
(2 балла) Найдите значение выражения ![]()
8. (2 балла) Решите уравнение
cos х =![]() . Запишите
наименьший положительный корень уравнения.
. Запишите
наименьший положительный корень уравнения.
9. Решите уравнение sin2 х - 4 sin х + 3 =0.
10. Постройте график тригонометрической функции y=2 sinx
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Б |
А |
В |
Б |
1 |
2π |
7 |
π/3 |
π/2+2πn, n∈ Z |
|
Производная и первообразная функции
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 4, ДРб 6, ДРб 14.
ОК 01, ОК 03, ОК 06.
ПК 1.4.
Теоретические вопросы:
1. Продолжите определение: «Производная – это…».
2. Раскройте геометрический смысл производной.
3. Раскройте физический смысл производной.
4. Перечислите правила вычисления производных.
5. Чему равна производная степенной функции?
6. Чему равна производная произведения?
7. Чему равна производная частного?
8. Чему равна производная сложной функции?
9. Сформулируйте признак возрастания функции.
10. Сформулируйте признак убывания функции.
11. Сформулируйте признак точки максимума функции.
12. Сформулируйте признак точки минимума функции.
13. Составьте алгоритм решения задач на нахождения наибольшего и наименьшего значения функции на отрезке?
14. Составьте алгоритм исследования и построения графика функции с помощью производной.
15. Продолжите определение: «Функция F(x) называется …».
16. Раскройте геометрический смысл определенного интеграла.
17. Продолжите определение: «Криволинейная трапеция – это…».
18. Сформулируйте формулу Ньютона-Лейбница.
19. В чем заключается общий вид всех первообразных?
20. Перечислите правила вычисления интегралов.
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) Чему равна производная функции у=2х3?
А) у´= 5х; Б) у´= 6х; В) у´= 6; Г) у´=6х2.
2. (1 балл) По какой из формул вычисляется производная частного?
А)
(u+v)´=u´+v´; Б) (uv)´=u´v+uv´; В)![]() ;
Г)(f(g(х))´=f´(g(х))*g´(х).
;
Г)(f(g(х))´=f´(g(х))*g´(х).
3. (1 балл) Решите уравнение f´(х)=0, если f(х)=3х2 – 6х +4. Выберите ответ.
А) 1; Б) -1; В) 4; Г) -4.
4. (1 балл) Общий вид всех первоообразных для f(х)=sinx?
А) F(х)=cosx+C; Б) F(х)=-cosx+C; В) F(х)=tgx+C; Г) F(х)=-tgx+C.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5.
(2 балла) Материальная точка движется прямолинейно по
закону ![]() (где x — расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала движения). В какой момент времени (в
секундах) ее скорость была равна 5 м/с?
(где x — расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала движения). В какой момент времени (в
секундах) ее скорость была равна 5 м/с?
6. (2 балла) На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
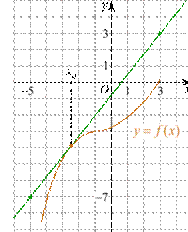
7. (2 балла) Решите неравенство: х2-16 < 0
8. (2 балла) На рисунке изображен график функции y=f(x), определённой на интервале (−3; 11). Найдите наименьшее значение функции f(x)на отрезке [2; 9,5].
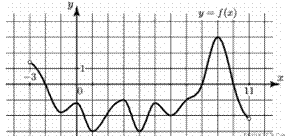
9. (2
балла) На рисунке изображён график некоторой функции ![]() (два луча с общей начальной точкой). Пользуясь
рисунком, вычислите
(два луча с общей начальной точкой). Пользуясь
рисунком, вычислите ![]() где
где ![]() —
одна из первообразных функции
—
одна из первообразных функции ![]()
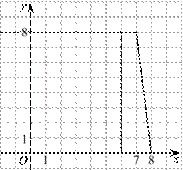
10. (2 балла) Фирме «Дизайн+» выделяют участок земли площадью 100 м2. Предлагают четыре участка разных размеров: 25х4; 20х5; 12,5х8; 10х10. Какой участок одобрит директор фирмы «Дизайн+»», учитывая, что необходимо будет поставить забор по периметру?
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Г |
В |
А |
Б |
8 |
1,25 |
(-4; 4) |
-3 |
12 |
10х10 |
Многогранники и тела вращения
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 6, ДРб 9, ДРб 10, ДРб 11, ДРб 12, ДРб 14.
ОК 01, ОК 03, ОК 05, ОК 06, ОК 7.
ПК 1.1, ПК 1.2.
Теоретические вопросы:
1. Продолжите определение: «Многогранник – это…».
2. Продолжите определение: «Призма – это…».
3. Продолжите определение: «Прямоугольный параллелепипед – это…».
4. Продолжите определение: «Куб – это…».
5. Продолжите определение: «Пирамида – это…».
6. Сформулируйте свойство о противолежащих гранях параллелепипеда.
7. Сформулируйте свойство о диагоналях параллелепипеда.
8. Сформулируйте свойство о диагонали и линейных размерах прямоугольного параллелепипеда.
9. Какая призма называется прямой?
10. Какая призма называется правильной?
11. Раскройте понятие «правильная пирамида».
12. Что такое апофема правильной пирамиды?
13. В чем отличие полной поверхности призмы от полной поверхности пирамиды?
14. Сформулируйте теорему о вычислении боковой поверхности прямой призмы.
15. Сформулируйте теорему о вычислении боковой поверхности правильной пирамиды.
16. Назовите предметы из вашей профессиональной деятельности, которые имеют формы многогранников.
17. Продолжите определение: «Цилиндр – это…».
18. Продолжите определение: «Конус – это…».
19. Продолжите определение: «Усеченный конус – это…».
20. Продолжите определение: «Шар – это…».
21. Что является высотой усеченного конуса?
22. Что является осевым сечением цилиндра, конуса, усеченного конуса, шара?
23. Перечислите единицы измерения площади, объема.
24. Чему равно отношение площадей поверхностей подобных фигур в пространстве?
25. Чему равно отношение объемов подобных фигур в пространстве?
26. Назовите предметы из вашей профессиональной деятельности, которые имеют формы тел вращения.
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) В каких единицах измеряется объем многогранника?
А) в метрах; Б) в кубических метрах; В) в квадратных метрах; Г) в двугранных градусах.
2. (1 балл) Площадь полной поверхности призмы вычисляется по формуле:
А) S = Sбок + 2 Sосн.; Б) Sбок =Росн*H; В) S = Ббок + S Sосн; Г) Sбок =2Росн*H.
3. (1 балл) Что является осевым сечением конуса?
А) равнобедренный треугольник; Б) равнобедренная трапеция; В) прямоугольник; Г) прямоугольная трапеция.
4. (1 балл) Какая фигура получается при вращении прямоугольного треугольника вокруг одного из своих катетов?
А) конус; Б) усеченный конус; В) пирамида; Г) усеченная пирамида.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5. (2 балла) Ребро основания правильной треугольной пирамиды 3 м, апофема 6м. Найдите площадь боковой поверхности пирамиды.
6. (2 балла) Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.

7. (2 балла) Прямоугольник со сторонами 8 см и 3 см вращается вокруг большей стороны. Найдите объем, площади боковой и полной поверхностей полученного тела.
8. (2 балла) Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
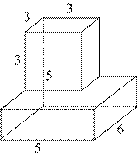
9. (2 балла) Клиенту необходимо, чтобы в комнате обязательно присутствовали объемные элементы декора цилиндрической формы. Построить из бумаги модель цилиндра. Размеры для построения выбрать самостоятельно, с учетом того, что соотношение радиуса к высоте должно быть 1:2.
10. (2 балла) Рассчитать количество 2-х килограммовых банок краски нужно купить для окрашивания цилиндрического свода подвала. Расход краски 100 г на 1 м2. Считать π=3.
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Б |
А |
А |
А |
27 |
17 |
72 π; 48 π; 64 π |
87 |
- |
3 |
Степенная, показательная и логарифмическая функции
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 2, ДРб 3, ДРб 4, ДРб 6, ДРб 14.
ОК 01, ОК 02, ОК 03, ОК 06.
Теоретические вопросы:
1. Сформулируйте определение степенной функции.
2. Перечислите свойства степенной функции
3. Сформулируйте определение показательной функции.
4. Перечислите свойства показательной функции
5. Сформулируйте определение логарифмической функции.
6. Перечислите свойства логарифмической функции.
7. Продолжите определение: «Логарифм – это…».
8. Чему равен логарифм произведения?
9. Чему равен логарифм частного?
10. Приведите примеры логарифмической спирали в природе и в окружающем мире.
11. На что необходимо обратить внимание при решении иррационального уравнения четной степени?
12. Чему равен корень четной степени из отрицательного числа? Приведите пример.
13. Чему равен корень нечетной степени из отрицательного числа? Приведите пример.
14. На что стоит обратить внимание при решении логарифмических и иррациональных, дробно-рациональных уравнений и неравенств?
15. В чем заключается графический способ решения уравнений.
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1.
(1 балл) Между
какими двумя натуральными числами находится число ![]() ?
?
А) 19 и 20; Б) 2 и 3; В) 18 и 19; Г) 3 и 4.
2. (1 балл) На рисунке изображён график функции вида f(x)=ax. Найдите значение f(2).
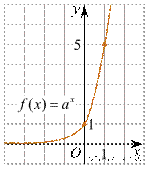
А) 25.; Б) 5; В) 32; Г) нет верного ответа.
3. (1 балл) Какая из функций возрастают на всей области определения?
А)
f(х)=![]() ; Б) f(х)=
; Б) f(х)=![]() В) f(х)=х2; Г) f(х)=
В) f(х)=х2; Г) f(х)=![]() .
.
4.
(1
балл) Укажите
область определения функции ![]()
А) (-7; 1,5); Б) (-∞; -1,5), (7; +∞).; В) (-1,5; 7); Г) (-∞; -7), (1,5; +∞).
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5.
(2 балла) Найдите значение выражения ![]()
6. (2 балла) Сколько целых решений имеет неравенство1<7х-1≤49?
7.
(2 балла) Найдите корень уравнения ![]()
8.
(2 балла)) Расстояние от
наблюдателя, находящегося на небольшой высоте h километров над землёй, до наблюдаемой им линии
горизонта вычисляется по формуле ![]() , где R=6400 км — радиус Земли. С какой высоты горизонт виден
на расстоянии 48 километров? Ответ выразите в километрах.
, где R=6400 км — радиус Земли. С какой высоты горизонт виден
на расстоянии 48 километров? Ответ выразите в километрах.
9. (2 балла) В ходе распада радиоактивного
изотопа его масса уменьшается по закону ![]() где m0 — начальная масса изотопа, t —
время, прошедшее от начального момента, T — период полураспада. В
начальный момент времени масса изотопа 184 мг. Период его полураспада составляет
7 мин. Найдите, через сколько минут масса изотопа будет равна 23 мг.
где m0 — начальная масса изотопа, t —
время, прошедшее от начального момента, T — период полураспада. В
начальный момент времени масса изотопа 184 мг. Период его полураспада составляет
7 мин. Найдите, через сколько минут масса изотопа будет равна 23 мг.
10. (2 балла)![]()
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Б |
А |
А |
Г |
121 |
2 |
21 |
0,18 |
21 |
3 |
Элементы теории вероятностей и математической статистики
Образовательные результаты, подлежащие проверке (элементы):
ДРб 7, ДРб 8, ДРб 14.
ОК 01, ОК 03, ОК 04, ОК 05.
ПК 1.4.
Теоретические вопросы:
1. Продолжите определение: «Случайное событие – это…». Приведите пример.
2. Приведите пример достоверного события.
3. Приведите пример невозможного события.
4. Продолжите определение: «Вероятность случайного события – это…».
5. Сформулируйте правило нахождения сложения вероятностей.
6. Сформулируйте правило умножения вероятностей.
7. Как найти среднее арифметическое числового ряда?
8. Как найти медиану числового ряда?
9. Как вычисляется размах числового ряда?
10. Для чего нужны диаграммы, графики? Перечислите виды диаграмм.
11. Приведите примеры проявления закона больших чисел в природных явлениях.
12. Приведите примеры проявления закона больших чисел в общественных явлениях.
13. Что изучает статистика?
14. Продолжите определение: «Сочетание – это…».
15. Продолжите определение: «Размещение – это…».
16. Продолжите определение: «Перестановки – это…».
Контрольная работа
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных
1. (1 балл) Каких событий не бывает в теории вероятностей?
А) случайные; Б) неслучайные; В) достоверные; Г) невозможные.
2. (1 балл) Событие, которое при выполнении определенной совокупности условий, обязательно произойдет - это:
А) случайное; Б) неслучайное; В) достоверное; Г) невозможное.
3. (1 балл) Вероятность случайного события есть неотрицательное число, заключенное между числами:
А) 0 и 1; Б) 0 и 100; В) -1 и 1; Г) -100 и 100.
4. (1 балл) Группировка – это…
А) упорядочение единиц совокупности по признаку; Б) разбиение единиц совокупности на группы по признаку; В) обобщение единичных фактов; Г) обобщение единичных признаков.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5. (2 балла) В офисе дизайнерского агентства находятся 8 посетителей женского пола и 2 мужского. Определить вероятность того, что первым к консультанту обратится мужчина.
6. (2 балла) На конференцию приехали 2 ученых из Германии, 3 из Сербии и 7 из Швейцарии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что пятым окажется доклад ученого из Сербии.
7. (2 балла) Маша, Тимур, Диана, Костя и Антон бросили жребий — кому достанется проект по оформлению свадебного зала. Найдите вероятность того, что проект точно не будет выполнять Антон.
8. (2 балла) В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
9. (2 балла) Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169. Найдите моду ряда и среднее арифметическое ряда.
10. (2 балла) При анализе ценовых предпочтений клиентов дизайнерского агентства получены данные, представленные в таблице: доля клиентов, приобретающих дизайнерские услуги одинакового назначения, но различной цены. Найти моду случайной величины. Х – цены продаваемых услуг.
|
xi |
3500 |
4500 |
5500 |
6500 |
7500 |
8500 |
|
pi |
1/20 |
3/20 |
3/20 |
8/20 |
4/20 |
1/20 |
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Б |
В |
А |
А |
0,2 |
0,25 |
0,8 |
0,15 |
172; 172,75 |
6500 |
4.Фонд оценочных средств для рубежного контроля
(по итогам 3.1 – 3.3, I семестр)
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 3, ДРб 4, ДРб 5, ДРб 6, ДРб 9, ДРб 11, ДРб 12, ДРб 13, ДРб 14.
ОК 01, ОК 02, ОК 03, ОК 05, ОК 06.
ПК 1.2, ПК 1.4.
Первая часть
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. Даны точки А(2,0,5), В(-2,6,3). Какие координаты имеет середина отрезка АВ – точка М?
А) М(0, 3, 4); Б) М(2, 3, 4); В) М(0,- 3, 4); Г) М(0, 3,- 4).
2. (1 балл) Прямые АВ и СД параллельные. Какое расположение имеют прямые АС и ВД?
А) параллельные; Б) перпендикулярные; В) скрещиваются; Г) пересекаются.
3. (1 балл) Какие из функций являются чётными?
А) у=sin х; Б) у=cos х; В) у=tg х; Г) у= сtg х.
4. (1 балл) На рисунке изображен график производной функции y=f(x). При каком значении x функция принимает свое наибольшее значение на отрезке [-4; -2] ?
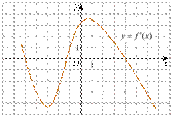
А) 0,5; Б) -4; В) -5; Г) 1.
Вторая часть
При выполнении заданий 5-10 запишите ход решения и полученный ответ.
5. (2 балла) Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если АА1=6 см, ВВ1=4 см.
6. (2 балла) Даны точки А(6,7,8) , В(8,2,6). Найдите длину вектора АВ.
7.
(2 балла) Найдите ![]() если
если ![]()
8. (2 балла) Материальная точка движется прямолинейно по закону x(t)=t2-13t+23 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
9. (2 балла) Дана функция f(х)= 3х2+1. Чему равна F(1)?
10. (2 балла) Решите уравнение cosx=1. В ответ запишите наименьший неотрицательный корень.
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
А |
Г |
Б |
Б |
5 |
|
-2 |
8 |
2 |
0 |
5. Фонд оценочных средств для промежуточной аттестации (экзамен)
Оценка освоения предмета предусматривает проведение экзамена.
5.1 Письменная экзаменационная работа:
На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240 минут).
Экзаменационная работа состоит их 2-х частей: обязательной и дополнительной.
Обязательная часть содержит задания минимального обязательного уровня, дополнительная часть – более сложные задания.
При выполнении заданий обязательной части требуется представить ход решения и указать полученный ответ. За правильное выполнение любого задания из обязательной части обучающийся получаете один балл. При выполнении задания из дополнительной части необходимо подробно описать ход решения и дать ответ. Правильное выполнение заданий дополнительной части оценивается 3 баллами или 1-2 баллами за частичное решение.
Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«3» (удов.) |
6-9 |
|
«4» (хорошо) |
10-14 (не менее одного задания из дополнительной части) |
|
«5» (отлично) |
более 14 (не менее двух заданий из дополнительной части) |
Образовательные результаты, подлежащие проверке (элементы):
ДРб 1, ДРб 2, ДРб 3, ДРб 4, ДРб 5, ДРб 6, ДРб 7, ДРб 8, ДРб 9, ДРб 10, ДРб 11, ДРб 12, ДРб 13, ДРб 14.
ОК 01, ОК 02, ОК 03, ОК 04, ОК 05, ОК 06, ОК 07.
ПК 1.2, ПК 1.4.
Экзаменационные задания по математике
Обязательная часть
При выполнении заданий 1-12 запишите ход решения и полученный ответ.
1. (1 балл) Вычислите: 2sin(π/6)+2cos(π/3)
2. (1 балл) На рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков?
![]()
3. (1 балл) Стоимость услуг частного дизайнера возросла на 10%. Определить, сколько стоили услуги дизайнера до подорожания, если после клиент заплатил 55000руб?
4. (1 балл) На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
5. (1 балл) Найдите значение выражения log22 + log2 32
6.
(1
балл) Найдите
корень уравнения ![]()
7. (1 балл) Решите неравенство 2х+5 > 64. В ответ запишите наименьшее положительное число.
8.
(1
балл) Найдите
корень уравнения ![]()
9.
(1
балл) Найдите
производную функции в точке х=0:![]()
10.
(1
балл) Кастрюля,
оформленная по индивидуальному заказу, имеет форму цилиндра. Высота кастрюли 35
см, диаметр основания 20 см. Рассчитайте вместимость данной посуды, деленную на ![]()
11. (1 балл) Найдите площадь фигуры, изображенной на рисунке
![]()
12. (1 балл) Тело движется по закону S(t)=3t2+5t (м) Найти скорость тела через 1с после начала движения.
Дополнительная часть
При выполнении заданий 13-16 запишите ход решения и полученный ответ
13. (3 балла) Вычислите площадь участка стола, отведенного для презентации работ дизайнера Василия, периметр которого ограничивают линии у=x2-2x-2 и
у=-x2+2. Выполните чертеж. Ответ дайте в квадратных метрах.
14. (3 балла) Решите уравнение
sin2x - 2sinx=0. В ответ запишите количество решений, принадлежащих
промежутку [0; 4![]() ]
]
15. (3 балла) Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
![]()
16. (3 балла) Заказ на 126 открыток первый дизайнер выполняет на 5 часов быстрее, чем второй. Сколько открыток за час изготавливает первый дизайнер, если известно, что он за час может приготовить на 5 открыток больше второго?
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Ответ |
2 |
3 |
50 тыс |
0,25 |
6 |
-7 |
1 |
-10 |
7 |
3500 |
15 |
11 |
9 |
5 |
6 |
13 |
5.2 Письменная экзаменационная работа:
Вариант проведения экзаменационной работы по билетам.
Каждый билет состоит из двух вопросов и практической части.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
Вопрос №1
Определение комплексного числа в алгебраической форме, действия над комплексными числами в алгебраической форме.
Вопрос №2
Первый и второй замечательные пределы.
Вычислить: ![]() .
.
Практическое задание
Найти
производную функции ![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2
Вопрос №1
Определение производной функции, её физический и геометрический смысл.
Вопрос №2
Действия над комплексными числами, заданными в алгебраической форме.
Вычислить:
![]() .
.
Практическое задание
Найти
скалярное произведение векторов![]() , если
, если ![]() ,
, ![]()
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3
Вопрос №1
Дифференцирование сложных функций.
Вопрос №2
Решение квадратных уравнений с отрицательным дискриминантом.
Решить уравнение: ![]() .
.
Практическое задание
Составить уравнение окружности с центром в точке (5;-7) и проходящей через точку (2;-3).
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4
Вопрос №1
Определение производной функции, её физический и геометрический смысл.
Вопрос №2
Определение матрицы. Действия над матрицами, их свойства. Найти произведение матриц
![]() .
.
Практическое задание
Вычислить:
![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5
Вопрос №1
Определение комплексного числа в алгебраической форме, действия над комплексными числами в алгебраической форме.
Вопрос №2
Определители 2-го и 3-го порядков. Определители n-го порядка. Свойства определителей.
Вычисление
определителей. Вычислить определитель 2-го порядка: ![]() .
.
Практическое задание
Найти:
![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6
Вопрос №1
Определение комплексного числа в алгебраической форме, действия над комплексными числами в алгебраической форме.
Вопрос №2
Первый и второй замечательные пределы.
Вычислить: ![]() .
.
Практическое задание
Найти
матрицу ![]() , если
, если 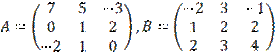 .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7
Вопрос №1
Формулы Крамера для решения систем линейных уравнений.
Вопрос №2
Определение
вектора. Операции над векторами, их свойства. Найти сумму векторов, заданных
своими координатами: ![]() .
.
Практическое задание
Вычислить
предел: ![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8
Вопрос №1
Определение производной функции, её физический и геометрический смысл.
Вопрос №2
Координаты
вектора. Модуль вектора. Скалярное произведение векторов. Найти модуль вектора ![]() .
.
Практическое задание
Найти
значение выражения: ![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9
Вопрос №1
Приближенные числа. Абсолютная и относительная погрешность. Приближенные вычисления.
Вопрос №2
Правила
и формулы дифференцирования. Дифференцируемость функции. Дифференциал функции.
Найти производную произведения: ![]() .
.
Практическое задание
Найти
скалярное произведение векторов ![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10
Вопрос №1
Приближенные числа. Абсолютная и относительная погрешность. Приближенные вычисления.
Вопрос №2
Правила
и формулы дифференцирования. Дифференцируемость функции. Дифференциал функции.
Найти производную произведения: ![]() .
.
Практическое задание
Найти
все алгебраические дополнения матрицы ![]() .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11
Вопрос №1
Решение системы n линейных уравнений с n неизвестными методом Гаусса.
Вопрос №2
Исследование
функций с помощью производной: интервалы монотонности и экстремумы функций.
Исследовать функцию на монотонность: ![]() .
.
Практическое задание
Вычислить
определитель 3-го порядка 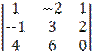 .
.
5.3 Контрольно-оценочные материалы для промежуточной аттестации по учебному предмету
Вопросы (задания) к экзамену по учебному предмету
I вариант
1. Вычислить предел:
![]()
2.
Найти производную сложной функции: ![]()
3.
Исследовать функцию на монотонность и экстремумы с помощью первой производной:
![]()
4.
Найти неопределенный интеграл методом подстановки: ![]()
5. Найти площадь фигуры, ограниченной линиями:
y = x2 + 1, y = 0, x = -1, x = 2. Выполнить рисунок.
6. Найти скалярное произведение векторов и угол между ними:
![]() ,
, ![]()
7. По стороне основания а и боковому ребру l вычислить объём правильной четырехугольной призмы
8. Диагональ осевого сечения цилиндра равна d и наклонена к плоскости основания под углом α. Найти площадь полной поверхности и объем цилиндра.
9.
Найти разложение степени бинома: ![]()
10. В закрытой корзине 30 шаров, из них 12 красных, 8 синих, 10 белых. Какова вероятность достать из корзины наугад 2 цветных шара?
II вариант
1.
Вычислить предел: ![]()
2.
Найти производную сложной функции: ![]()
3. Исследовать функцию на монотонность и экстремумы с помощью первой
производной:
![]()
4.
Найти неопределенный интеграл методом подстановки: ![]()
5. Найти площадь фигуры, ограниченной линиями:
y = x2, y = 0, x = 0, x = 3 . Выполнить рисунок.
6. Найти скалярное произведение векторов и угол между ними:
![]() ,
, ![]()
7. В правильной четырехугольной призме диагональ длиной l составляет с боковой
гранью угол α. Найти площадь боковой поверхности призмы.
8. Угол при вершине осевого сечения конуса равен α, высота конуса равна h.
Найти площадь боковой поверхности и объём конуса.
9.
Найти четвертый член разложения бинома: ![]()
10. В закрытой коробке 20 карандашей, из них 5 синих, 4 красных, остальные черные. Какова вероятность достать из коробки наугад 3 цветных карандаша?
Направленность освоенных результатов на формирование ОК:
|
Код компетенций |
Проверяемые результаты обучения, ОК |
Вид задания (вопрос) |
|
ОК 01. |
Выбирать способы решения задач профессиональной деятельности
применительно
|
Вариант 1, задания 1, 2, 3, 4 Вариант 2, задания 1, 2, 3, 4 |
|
ОК 02 |
Использовать современные средства поиска, анализа и
интерпретации информации, и информационные технологии для выполнения |
Вариант 1, задания 4, 5, 6 Вариант 2, задания 4, 5, 6 |
|
ОК 03 |
Планировать
и реализовывать собственное |
Вариант 1, задания 1, 7, 8 Вариант 2, задания 1, 7, 8 |
|
ОК 04 |
Эффективно взаимодействовать и работать в коллективе и команде |
Вариант 1, задания 1, 2, 3, 9, 10 Вариант 2, задания 1, 2, 3, 9, 10 |
|
ОК 05 |
Осуществлять
устную и письменную |
Вариант 1, задания 1, 2, 3, 4, 5, 9, 10 Вариант 2, задания 1, 2, 3, 4, 5, 9, 10 |
|
ОК 06 |
Проявлять
гражданско- патриотическую позицию, демонстрировать осознанное поведение на |
Вариант 1, задания 6, 7, 8 Вариант 2, задания 6, 7, 8
|
|
ОК 07 |
Содействовать
сохранению окружающей |
Вариант 1, задания 3, 5 Вариант 2, задания 3, 5 |
Критерии и шкалы для интегрированной оценки уровня сформированности компетенций:
|
Индикаторы компетенции |
неудовлетворительно |
удовлетворительно |
хорошо |
отлично |
|
Полнота знаний |
Уровень знаний ниже минимальных требований. Имели место грубые ошибки. |
Минимально допустимый уровень знаний. Допущено много не грубых ошибки. |
Уровень знаний в объеме, соответствующем программе подготовки. Допущено несколько не грубых ошибок |
Уровень знаний в объеме, соответствующем программе подготовки, без ошибок. |
|
Наличие умений |
При решении стандартных задач не продемонстрированы основные умения. Имели место грубые ошибки. |
Продемонстрированы основные умения. Решены типовые задачи с не грубыми ошибками. Выполнены все задания но не в полном объеме. |
Продемонстрированы все основные умения. Решены все основные задачи с не грубыми ошибками. Выполнены все задания, в полном объеме, но некоторые с недочетами. |
Продемонстрированы все основные умения, решены все основные задачи с отдельными несущественным недочетами, выполнены все задания в полном объеме. |
|
Характеристика сформированности компетенции |
Компетенция в полной мере не сформирована. Имеющихся знаний, умений, навыков недостаточно для решения практических (профессиональных) задач. Требуется повторное обучение |
Сформированность компетенции соответствует минимальным требованиям. Имеющихся знаний, умений, навыков в целом достаточно для решения практических (профессиональных) задач, но требуется дополнительная практика по большинству практических задач. |
Сформированность компетенции в целом соответствует требованиям, но есть недочеты. Имеющихся знаний, умений, навыков и мотивации в целом достаточно для решения практических (профессиональных) задач, но требуется дополнительная практика по некоторым профессиональным задачам. |
Сформированность компетенции полностью соответствует требованиям. Имеющихся знаний, умений, навыков и мотивации в полной мере достаточно для решения сложных практических (профессиональных) задач. |
|
Уровень сформированности компетенций |
Низкий |
Ниже среднего |
Средний |
Высокий |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.