Тема урока: «Преобразование произведений тригонометрических функций в суммы».

 

Тема урока: «Преобразование произведений тригонометрических функций в суммы». (Слайд 1)

 

Тип урока: урок изучения нового материала и систематизации знаний.

Цели:

Образовательные: ознакомить учащихся с формулами преобразования произведения тригонометрических функций в сумму или разность, закрепить умения и навыки по применению формул тригонометрии при решении задач.

 Развивающие: развивать и совершенствовать умения применять теоретические знания к решению упражнений; мыслительные способности учащихся; их речевую культуру; математический кругозор.

Воспитательные: воспитывать уверенность в своих знаниях; умение слушать других; содействовать воспитанию интереса к математике; воспитывать объективность и честность при контроле знаний; культуру поведения.

 

Задачи урока:

●        Создать условия для формирования у обучающихся представлений о формулах для преобразования произведения тригонометрических функций в сумму или разность;

●        Создать условия для мотивации обучающихся в изучении формул преобразования произведения тригонометрических функций в сумму или разность;

●        способствовать формированию умений в применении нового и ранее изученного материала, при выполнении различных преобразований тригонометрических выражений;

●        способствовать формированию таких качеств личности как ясность и точность мысли, самоконтроль;

●        продолжить формировать представления о математике как части общечеловеческой культуры и ее связи с другими науками.

 

Планируемые результаты: Сформировать навыки и умения применять формулы, преобразующие произведение тригонометрических функций в сумму или разность при выполнении различных заданий по тригонометрии.

Техническое обеспечение урока: компьютер, проектор, экран, доска, мел.

 

Содержание урока:

                                                   Ход урока

1.     Организационный момент.

 

2.     Проверка домашнего задания. Устная разминка: (Слайд 2)

1.     Какому выражению соответствует значение   ?

а) sin 30; б) cos ;    в) tg

2.     Выбрать возможный вариант.

а) siná =;    б) cos á  = -2;   в) sin á   = -3,7.

3.     Какой из углов является углом II четверти?

а) ;    б) –145^° ;    в)

4.     В каких четвертях siná    и  cos á  имеют разные знаки?

а) II и IV;   б) I и  III;   в) I и IV.

 

5.     Каким выражением можно заменить ?

                    а) cos á ;     б) siná ;    в) - siná.

 

1	2	3	4	5
б	б	в	а	в

 

3.     Изучение нового материала

На прошлом уроке мы рассмотрели преобразование суммы и разности тригонометрических функций в произведение. Сегодня мы рассмотрим обратное преобразование, т. е. представить произведение в виде суммы и разности.

Для вывода этих формул воспользуемся формулами сложения.

 

На уроке доказываются формулы преобразования произведений трех видов: синуса на синус, косинуса на косинус и синуса на косинус, решается несколько примеров на использование этих формул.

 

1). Формулы преобразования произведений тригонометрических функций в сумму (Слайд 3)

Доказать:

 

Доказательство:(вызвать 1 ученика)

 

1) Формулы синуса разности и суммы:

Складывая, получаем:

отсюда,

 

 

2) Формулы косинуса разности и суммы (вызвать 2 ученика)

 

 

Складывая, получаем:

Что можно записать:

 

3) Вычитая косинус суммы из косинуса разности, получим:

,

что преобразуется в формулу:

 

 

2). Закрепление изученного материала. Использование формул при решении задач

Вычислить, преобразовывая произведения в сумму.

1) (Слайд 4)

Решение:

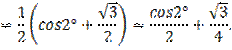
Ответ:

 

 

2)  (Слайд 5)

Решение:

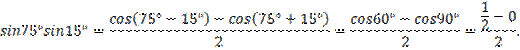
Ответ:

 

 

 

3)

(Слайд 6)

Решение: воспользуемся формулами:

Получим:

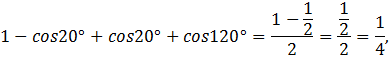
где

Ответ:

4) (Слайд 7)

Решение: воспользуемся формулами:

Получим:

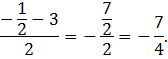
Ответ: 

 

 

3). Решение уравнения

1)   (Слайд 8)

Решение: воспользуемся формулой

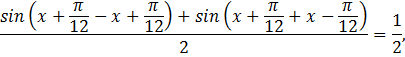
Ответ:

 

2)

  (Слайд 9)

Решение

 

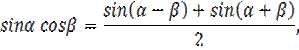
получим:

Ответ: 

 

4) Доказать тождество: (Слайд 10)

Доказательство:

 

 

5). Итог урока    На уроке рассматривались формулы, по которым произведения тригонометрических функций можно преобразовать в суммы. (Слайд 11)

 Продолжи фразу

«Сегодня на уроке я повторил…»

«Сегодня на уроке я закрепил…»

«Сегодня на уроке я узнал…»

 

Домашнее задание: п.23, №  23.1-23.5(в, г); № 23.10(а) (Слайд 12)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru