Тема урока: Свободные и вынужденные колебания

Тема урока: Свободные и вынужденные колебания

Задачи

Обучающая: определение понятий свободные и вынужденные колебание

Развивающая:  расширить естественнонаучную  систему взглядов на процессы, происходящие в природе, развитие зрительной памяти, внимания, смысловой памяти, умений анализировать, сравнивать, обобщать,.    

Воспитательная: развитие речи учащихся, наблюдательности, зрительного восприятия,  самостоятельности  в выдвижении гипотезы и формулирования выводов, воспитание коммуникативной культуры, умения оценивать себя и своих товарищей

Демонстрация: презентации

Цель урока: сформировать у учащихся представление о гармонических колебаниях, как о гармонических изменениях координаты и других физических величин; ввести понятие амплитуды, периода, частоты, циклической частоты; получить формулу для вычисления периода свободных колебаний.

Личностных:

Способствовать саморазвитию и самообразованию учащихся на основе мотивации к обучению и познанию.

Формировать целостную картину мира.

Формировать осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению.

Метапредметных:

Организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Создавать, применять и преобразовывать знаково-символические средства для решения задач.

Самостоятельно планировать пути достижения целей, осознано выбирать эффективные способы решения задач.

 Предметных:

Понимать смысл понятия  свободные и вынужденные колебание

Уметь описывать и объяснять свободные и вынужденные колебание

Делать выводы на основе теоретических данных.

Решать задачи на применение свободные и вынужденные колебание

Использовать приобретенные знания в повседневной деятельности

Планируемые результаты обучения:

-понимать смысл свободные и вынужденные колебание

-уметь объяснять свободные и вынужденные колебание

  -объяснять физические явления на основе знаний о основных параметрах гармонических колебаний

- использовать приобретенные знания и умения  в практической деятельности  и повседневной жизни

Личностные УУД: внутренняя позиция, мотивация.

Познавательные УУД: физическая модель поясняющая гармонические  колебания

Коммуникативные УУД: сотрудничество, вербальные  и невербальные способы коммуникации

Регулятивные УУД: постановка учебной цели, задачи.

Общеучебные умения, навыки и способы деятельности

                  Познавательная деятельность:

      •   использование для познания окружающего мира различных естественнонаучных методов:

      •    формирование умений различать факты, гипотезы, причины, следствия, доказательства, законы, теории;

      •  овладение адекватными способами решения теоретических и экспериментальных задач;

              Информационно-коммуникативная деятельность:

      •  владение монологической и диалогической речью, развитие способности понимать точку зрения собеседника и признавать право на иное мнение;

      •  использование для решения познавательных и коммуникативных задач различных источников информации.

         Рефлексивная деятельность:

      •  владение навыками контроля и оценки своей деятельности,

      • организация учебной деятельности: постановка цели, планирование, определение оптимального соотношения цели и средств.

Тип урока: урок изучения нового материала и формирования знаний, умений, навыков, возможности их применения на практике.

Формы работы учащихся:  индивидуальная,  фронтальная, работа в паре.

Выполнила: Керимова Ирина С.

План урока

I.Организационный момент

II.Работа над ошибками

III. Подготовка к активной учебной деятельности                                       Великий итальянский ученый Галилео Галилей всю жизнь посвятил физике и астрономии, сделав ряд важнейших открытий. Уже в студенческие годы Галилей увлекся изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса. Сохранилось придание о том, как молодой студент медицинского факультета Галилео Галилей в одно из воскресений 1583 года с интересом следил за качанием лампад в церкви. По ударам пульса он определил время, необходимое для полного размаха лампад. С этого времени ему пришлось медицину оставить и сосредоточиться на физике.

Голландский физик и математик, механик и астроном Христиан Гюйгенс, опираясь на исследования Галилео Галилея, решил ряд задач механики и в 1656 году в возрасте 27 лет сконструировал первые маятниковые часы со спусковым механизмом.

IV.Сообщение нового материала-

              Мы будем изу­чать так на­зы­ва­е­мые сво­бод­ные ко­ле­ба­ния – ко­ле­ба­ния, ко­то­рые си­сте­ма про­из­во­дит под дей­стви­ем пер­во­на­чаль­но за­па­сен­ной энер­гии. Но в ре­аль­но­сти такие ко­ле­ба­ния встре­ча­ют­ся неча­сто. Итак, нач­нем с пер­во­го раз­де­ла – гар­мо­ни­че­ских ко­ле­ба­ний.

Гар­мо­ни­че­ские ко­ле­ба­ния мы изучали ещё в 9 классе , когда сле­ди­ли за по­ве­де­ни­ем пру­жин­но­го и ма­те­ма­ти­че­ско­го ма­ят­ни­ков. Что же это за вид ко­ле­ба­ний? Мы пом­ним, что для воз­ник­но­ве­ния ко­ле­ба­тель­но­го дви­же­ния необ­хо­ди­мо, чтобы в си­сте­ме было по­ло­же­ние устой­чи­во­го рав­но­ве­сия, при вы­во­де из ко­то­ро­го воз­ни­ка­ет сила, стре­мя­ща­я­ся вер­нуть тело в это по­ло­же­ние. Если эта сила (воз­вра­ща­ю­щая сила) про­пор­ци­о­наль­на ве­ли­чине от­кло­не­ния тела от по­ло­же­ния рав­но­ве­сия, то го­во­рят, что си­сте­ма со­вер­ша­ет гар­мо­ни­че­ские ко­ле­ба­ния.                                                                                                                             Ха­рак­тер­ной чер­той гар­мо­ни­че­ских ко­ле­ба­ний яв­ля­ет­ся неза­ви­си­мость пе­ри­о­да таких ко­ле­ба­ний от ам­пли­ту­ды. Имен­но гар­мо­ни­че­ские ко­ле­ба­ния яв­ля­ют­ся са­мы­ми про­сты­ми с точки зре­ния ма­те­ма­ти­че­ско­го опи­са­ния та­ко­го дви­же­ния. От­лич­ны­ми мо­де­ля­ми для гар­мо­ни­че­ских ко­ле­ба­ний яв­ля­ют­ся пру­жин­ный и ма­те­ма­ти­че­ский ма­ят­ни­ки. Да­вай­те вспомним гар­мо­ни­че­ские ко­ле­ба­ния на при­ме­ре пру­жин­но­го ма­ят­ни­ка.

Пру­жин­ный ма­ят­ник                                                                                     Пусть воз­вра­ща­ю­щая сила (в дан­ном слу­чае сила упру­го­сти) опре­де­ля­ет­ся фор­му­лой: ,.За­пи­шем вто­рой закон Нью­то­на для дан­ной си­сте­мы: . Мы до­го­во­ри­лись, что в дан­ном слу­чае дей­ству­ет толь­ко сила упру­го­сти. Итак, мы по­лу­ча­ем: . Раз­де­лим это вы­ра­же­ние на массу m и по­лу­чим вы­ра­же­ние для уско­ре­ния ко­леб­лю­ще­го­ся тела: .  Ре­шить такое урав­не­ние стро­го ма­те­ма­ти­че­ски, такие урав­не­ния на­зы­ва­ют­ся диф­фе­рен­ци­аль­ны­ми. Ре­ше­ние будет вы­ра­жать­ся пе­ри­о­ди­че­ским за­ко­ном – за­ко­ном си­ну­са или ко­си­ну­са.

мы ав­то­ма­ти­че­ски узна­ем уг­ло­вую ча­сто­ту ко­ле­ба­ний, а, зная уг­ло­вую ча­сто­ту, мы можем вы­чис­лить ли­ней­ную ча­сто­ту или пе­ри­од ко­ле­ба­ний: .      

Толь­ко что мы по­лу­чи­ли вы­ра­же­ние для уг­ло­вой ча­сто­ты пру­жин­но­го ма­ят­ни­ка, ана­ло­гич­ным об­ра­зом можно по­лу­чить вы­ра­же­ние для уг­ло­вой ча­сто­ты ма­те­ма­ти­че­ско­го ма­ят­ни­ка, есте­ствен­но, там роль этого ко­эф­фи­ци­ен­та будут вы­пол­нять дру­гие ве­ли­чи­ны.

За­ви­си­мость E(t) при сво­бод­ных ко­ле­ба­ни­ях

Вы уже зна­е­те, что энер­гия во время ко­ле­ба­ний непре­рыв­но ме­ня­ет­ся: ки­не­ти­че­ская пе­ре­хо­дит в по­тен­ци­аль­ную и на­о­бо­рот. Ло­гич­но, что так же, как и ко­ор­ди­на­та, ско­рость, и уско­ре­ние, энер­гия будет ме­нять­ся по гар­мо­ни­че­ско­му за­ко­ну. Итак, как же про­ис­хо­дит пре­вра­ще­ние энер­гии при ко­ле­ба­ни­ях ма­ят­ни­ка? В верх­ней точке мак­си­маль­на по­тен­ци­аль­ная энер­гия, а ки­не­ти­че­ская равна 0

        Когда от­пу­стим ма­ят­ник, он нач­нет ко­ле­бать­ся. Рас­смот­рим ма­ят­ник, когда он про­хо­дит по­ло­же­ние рав­но­ве­сия: здесь ки­не­ти­че­ская мак­си­маль­ная, а по­тен­ци­аль­ная 0. По­тен­ци­аль­ная энер­гия равна 0, по­то­му что мы вы­бе­рем имен­но этот уро­вень (см. рис. 3), а не уро­вень земли.

Даль­ше про­ис­хо­дит об­рат­ное пре­вра­ще­ние энер­гии: ки­не­ти­че­ская на­чи­на­ет па­дать, а по­тен­ци­аль­ная уве­ли­чи­вать­ся (и так про­ис­хо­дит по­сто­ян­но). Те­перь по­пы­та­ем­ся вы­ве­сти закон, по ко­то­ро­му ме­ня­ют­ся по­тен­ци­аль­ная и ки­не­ти­че­ская энер­гии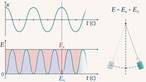

По­тен­ци­аль­ная энер­гия пру­жин­но­го ма­ят­ни­ка имеет вид: , Ки­не­ти­че­ская энер­гия: .

Ко­ор­ди­на­та ме­ня­ет­ся по та­ко­му за­ко­ну: .

Ско­рость тоже из­ме­ня­ет­ся по гар­мо­ни­че­ско­му за­ко­ну: .

Под­ста­вим вы­ра­же­ние для ко­ор­ди­на­ты и для ско­ро­сти в фор­му­лы для энер­гий и по­лу­чим закон, по ко­то­ро­му из­ме­ня­ет­ся со вре­ме­нем энер­гия по­тен­ци­аль­ная и ки­не­ти­че­ская для пру­жин­но­го ма­ят­ни­ка:   .

В каж­дый мо­мент вре­ме­ни сумма ки­не­ти­че­ской и по­тен­ци­аль­ной энер­гии оди­на­ко­ва – вы­пол­ня­ет­ся закон со­хра­не­ния энер­гии.    

В ре­аль­но­сти энер­гия, ко­неч­но же, не со­хра­ня­ет­ся. Любая ко­ле­ба­тель­ная си­сте­ма тра­тит часть своей энер­гии на пре­одо­ле­ние силы со­про­тив­ле­ния, силы тре­ния. Энер­гия умень­ша­ет­ся, ко­ле­ба­ния на самом деле яв­ля­ют­ся за­ту­ха­ю­щи­ми. 

Учтём, что си­сте­ма ма­ят­ни­ков неза­мкну­тая, то есть в си­сте­ме при­сут­ству­ет сила тре­ния. В ре­аль­ных усло­ви­ях мы можем взять тя­же­лый груз, под­ве­сить его на очень длин­ную и лег­кую нить или про­во­ло­ку, за­кре­пить один конец на опоре и по­лу­чить си­сте­му, близ­кую по своим свой­ствам к ма­те­ма­ти­че­ско­му ма­ят­ни­ку. Од­на­ко нель­зя ска­зать, что ме­ха­ни­че­ская энер­гия та­ко­го ма­ят­ни­ка будет со­хра­нять­ся – мы пре­крас­но знаем, что рано или позд­но он оста­но­вит­ся. В чем же наша недо­ра­бот­ка? Ответ прост: в дан­ной си­сте­ме при­сут­ству­ют раз­лич­ные виды тре­ния, дей­ствие ко­то­рых при­во­дит к по­те­ре на каж­дом пе­ри­о­де ко­ле­ба­ний ма­ят­ни­ка ка­кой-то части его энер­гии

Силы тре­ния могут быть внут­рен­ни­ми (на­при­мер, в под­ве­се ма­ят­ни­ка), а могут быть и внеш­ни­ми (на­при­мер, со сто­ро­ны окру­жа­ю­ще­го воз­ду­ха или дру­гой среды, в ко­то­рой может на­хо­дить­ся ма­ят­ник). Есте­ствен­но, что силы тре­ния за­ви­сят от свойств среды: в воде ко­ле­ба­ния будут за­ту­хать быст­рее, чем в воз­ду­хе . Боль­шин­ство ко­ле­ба­ний в мире – за­ту­ха­ю­щие, так как в окру­жа­ю­щем нас мире, по­сто­ян­но су­ще­ству­ют силы тре­ния.

 Вынужденные колебания                                                                        Итак, мы вы­яс­ни­ли: в ре­аль­но­сти ко­ле­ба­ния ма­ят­ни­ков ме­ха­ни­че­ских си­стем за­ту­ха­ю­щие, то есть их ам­пли­ту­да по­сте­пен­но умень­ша­ет­ся, стре­мясь к нулю. Что же нам сде­лать, чтоб ко­ле­ба­ния не были та­ки­ми, чтоб ам­пли­ту­да по­сто­ян­но под­дер­жи­ва­ла свое зна­че­ние? Для этого нам необ­хо­ди­мо разо­мкнуть си­сте­му и под­ка­чи­вать энер­гию извне. Таким об­ра­зом, мы до­бьем­ся неза­ту­ха­ю­щих ко­ле­ба­ний. Как же разо­мкнуть си­сте­му?                                                      Вспом­ним про­стой при­мер из жизни: ка­та­ние на ка­че­лях. Для того чтобы ка­че­ли ко­ле­ба­лись без оста­нов­ки, че­ло­век пе­ри­о­ди­че­ски тол­ка­ет их, а если пе­ре­ве­сти это на язык фи­зи­ки, то че­ло­век дей­ству­ет на ка­че­ли с силой, ве­ли­чи­на ко­то­рой за­ви­сит от вре­ме­ни пе­ри­о­ди­че­ским об­ра­зом.

Мы пре­крас­но по­ни­ма­ем, что если мы будем воз­дей­ство­вать на ка­че­ли по­сто­ян­но, то они не будут ко­ле­бать­ся.

Ко­ле­ба­ния си­сте­мы, со­вер­ша­ю­щие ею под дей­стви­ем внеш­ней пе­ри­о­ди­че­ской силы, на­зы­ва­ют­ся вы­нуж­ден­ны­ми. Силу, яв­ля­ю­щей­ся мерой этого внеш­не­го воз­дей­ствия, на­зы­ва­ют вы­нуж­да­ю­щей. . При­ме­ра­ми си­стем, в ко­то­рых со­вер­ша­ют­ся вы­нуж­ден­ные ко­ле­ба­ния, могут быть также в пол­нее при­выч­ные вам часы – это могут быть на­стен­ные ма­ят­ни­ко­вые часы, а могут быть и обыч­ные пру­жин­ные ме­ха­ни­че­ские часы. В каж­дом таком слу­чае ко­ле­ба­ния со­вер­ша­ют­ся за счет под­во­да энер­гии извне.

. Какой же ха­рак­те­ри­сти­кой долж­на об­ла­дать эта внеш­няя сила? Эта сила обя­за­тель­но долж­на ме­нять­ся во вре­ме­ни, долж­на быть пе­ри­о­ди­че­ской. И тут нужно по­го­во­рить о двух ча­сто­тах: соб­ствен­ная ча­сто­та ко­ле­ба­ний  – та ча­сто­та, с ко­то­рой бы ко­ле­ба­лась си­сте­ма, если бы она была вы­ве­де­на из рав­но­ве­сия и боль­ше её никто не со­об­щал её энер­гию (то есть никто бы боль­ше не рас­ка­чи­вал её), и ча­сто­та внеш­ней силы  – это та ча­сто­та, с ко­то­рой будут рас­ка­чи­вать ка­че­ли. За­пом­ни­те, чтобы ко­ле­ба­ния были вы­нуж­ден­ны­ми, внеш­няя сила долж­на пе­ри­о­ди­че­ски ме­нять­ся.                                                                                                   Резонанс                                                                                                 При­ве­дем ис­то­ри­че­ский факт: в Пе­тер­бур­ге силь­но рас­ка­чал­ся и в ре­зуль­та­те об­ва­лил­ся Еги­пет­ский мост (см. рис. 11).

Рис. 11. Обвал Еги­пет­ско­го моста

В это время по мосту мар­ше­вым шагом, то есть в ногу, про­хо­дил ка­ва­ле­рий­ский эс­кад­рон. По­че­му же в дан­ном слу­чае вы­нуж­ден­ные ко­ле­ба­ния (а имен­но: воз­дей­ствие эс­кад­ро­на и вы­зва­ло вы­нуж­ден­ные ко­ле­ба­ния) при­ве­ли к раз­ру­ше­нию моста?                                                                                                               . По­нят­но, что мост рас­ка­чал­ся до боль­шой ам­пли­ту­ды вслед­ствие того, что ча­сто­та его соб­ствен­ных ко­ле­ба­ний сов­па­ла с ча­сто­той внеш­не­го воз­дей­ствия, то есть ча­сто­той шагов эс­кад­ро­на. Без­услов­но, это слу­чай­ное сов­па­де­ние, од­на­ко ава­рию можно было предот­вра­тить, если перед вхо­дом на мост была бы от­да­на ко­ман­да «идти не в ногу», то есть идти враз­но­бой.

Об­ра­ти­те вни­ма­ние, когда ча­сто­та внеш­ней силы сов­па­ла с соб­ствен­ной ча­сто­той ко­ле­ба­ний, зна­че­ние ам­пли­ту­ды мак­си­маль­но – ам­пли­ту­да резко воз­рос­ла. Вывод: ам­пли­ту­да уста­но­вив­ших­ся вы­нуж­ден­ных ко­ле­ба­ний до­сти­га­ет сво­е­го наи­боль­ше­го зна­че­ния при усло­вии, что ча­сто­та вы­нуж­да­ю­щей силы равна соб­ствен­ной ча­сто­те ко­ле­ба­тель­ной си­сте­мы. Это яв­ле­ние на­зы­ва­ет­ся ре­зо­нан­сом.

По­че­му же на­сту­па­ет ре­зо­нанс? По­че­му ам­пли­ту­да резко воз­рас­та­ет при сов­па­де­нии ча­сто­ты внеш­ней силы и соб­ствен­ной ча­сто­ты ко­ле­ба­ний си­сте­мы?

В слу­чае ре­зо­нан­са на­прав­ле­ние вы­нуж­да­ю­щей силы в любой мо­мент вре­ме­ни сов­па­да­ет с на­прав­ле­ни­ем дви­же­ния ко­леб­лю­ще­го­ся тела, таким об­ра­зом, со­зда­ют­ся наи­бо­лее бла­го­при­ят­ные усло­вия для по­пол­не­ния энер­гии ко­ле­ба­тель­ной си­сте­мы за счет ра­бо­ты вы­нуж­да­ю­щей силы. На­при­мер, чтобы силь­ней рас­ка­чать ка­че­ли, мы под­тал­ки­ва­ем их таким об­ра­зом, чтобы на­прав­ле­ние дей­ству­ю­щей силы сов­па­да­ло с на­прав­ле­ни­ем дви­же­ния ка­че­ли. Важно пом­нить, что яв­ле­ние ре­зо­нан­са имеет от­но­ше­ние толь­ко к вы­нуж­ден­ным ко­ле­ба­ни­ям, то есть когда есть внеш­няя пе­ри­о­ди­че­ская вы­нуж­да­ю­щая сила.

Нель­зя го­во­рить, что ре­зо­нанс толь­ко пло­хое яв­ле­ние: на­при­мер, если стоит за­да­ча ми­ни­маль­ны­ми уси­ли­я­ми до­бить­ся мак­си­маль­но­го раз­ма­ха ко­ле­ба­ний (рас­ка­чи­ва­ние языка ко­ло­ко­ла (см. рис. 20)), то необ­хо­ди­мо до­бить­ся ча­сто­ты вы­нуж­да­ю­щей силы и соб­ствен­ной ча­сто­ты, то есть ис­поль­зо­вать ре­зо­нанс.

Закрепление материала

Механическое колебание – это движение, которое точно или приблизительно точно повторяется через равные промежутки времени, при котором тело смещается относительно положения равновесия, отклоняясь от него, то в одну, то в другую сторону.

Особенность механических колебаний – периодичность.

Свободными колебаниями называют колебания, которые совершает система под действием внутренних сил.

Систему тел, которая способна совершать свободные колебания, называют колебательной системой.

Свободные колебания затухающие или нет? Свободные колебания рано или поздно затухают и прекращаются, т.к. энергия уменьшается с течением времени. Обычно затухание происходит под действием сил сопротивления среды.

Условия существования свободных колебаний:

- наличие состояния устойчивого равновесия;

- наличие внутренней силы, возвращающей систему в состояние равновесия;

- наличие инертности, благодаря которой она не остается в состоянии равновесия;

- малое трение.

Величины, характеризующие колебательные движения:

Амплитуда (х_m)- максимальное расстояние, на которое тело отклоняется от положения равновесия .

Период (Т, ед. изм. с) - время одного полного колебания.

Т=t/n; Т=1/υ ;

Частота (υ, ед. изм. с^-1 или Гц) - число колебаний за единицу времени.

υ=n/t; υ=1/Т;

Пружинный маятник – модель колебательной системы; груз, прикрепленный к пружине.

Период свободных колебаний пружинного маятника: Т=2π√m/k

Математический маятник – модель колебательной системы; представляет собой небольшой груз, подвешенный на длинной нити.

Период свободных колебаний математического маятника: Т=2π√l/g

Гармоническими колебаниями называются такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону sin. или cos.

Колебания играют большую роль в жизни человека, в природе, технике.

V.Закрепление изученного материала

Задача. Груз колеблющийся на пружине, за 8 с совершил 32 колебания. Найти частоту и период колебаний.

Решение. Т=t/n; γ = 1/T; T= 8/32 = 0,25 c; γ= 1/0,25 = 4 Гц

VII. Домашнее задание: § 22,23

VIII. Подведение итогов. Рефлексия.  

Скачано с www.znanio.ru