
 Слайд
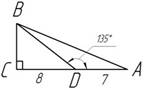
5. 3. Найдите площадь треугольника ABC.
Слайд
5. 3. Найдите площадь треугольника ABC.
Рис. 4. Чертеж к задаче 3
Ответ: 60 см2.
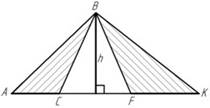
Рис. 8. Свойство площадей треугольников, имеющих общую высоту
Слайд 8. Если высоты треугольников равны, то площади относятся как основания.
SACB : SBFK = AC : FK
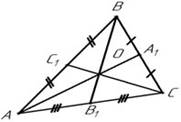
Рис. 9. Свойство медиан треугольника
Слайд 9. Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на 6 равновеликих треугольников.
Слайд 10. 1. Решите задачу:
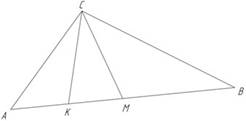
Рис. 10. Чертеж к условию задачи 1
Дано: CM – медиана ∆ABC, CK – медиана ∆ACM. SABC = 40 см2.
Найти: ![]()
Какую часть площадь одного треугольника составляет от площади другого?
Или. Во сколько раз площадь одного треугольника больше (меньше) площади другого?
Слайд 11. 2. Решите задачу:
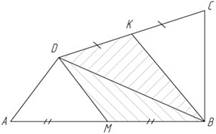
Рис. 11. Чертеж к условию задачи 2
Дано: ABCD – выпуклый четырёхугольник.
Доказать: SMBKD = SABCD : 2
Вопрос: Как относятся площади треугольников, имеющих по равному углу?
IV. Изучение новой темы
Слайд 12. Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы.
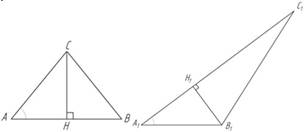
Рис. 12. Теорема о соотношении площадей треугольников, имеющих равный угол
Дано: ∆ABC, ∆A1B1C1, ∠A = ∠A1
Доказать:
![]()
V. Первичное закрепление
Учитель на экране показывает задачи, учащиеся предлагают свои решения задач
Слайд 14. Запишите отношение площадей
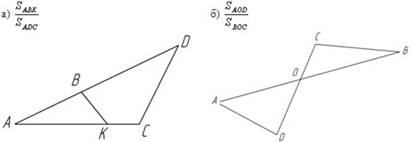
Рис. 14. Чертеж к пункту а) Рис. 15. Чертеж к пункту б)
![]()
Слайд 15
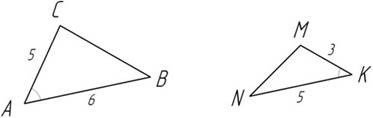
Рис. 16. Чертеж к условию задачи
Дано: ∠A = ∠K
Найти: SABC : SKMN = ?
Ответ: 30/15 или 2.
Слайд 16
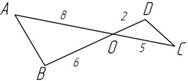
Рис. 17. Чертеж к условию задачи
Дано: SAOB = 20 см2.
Найти: SCOD = ?
Ответ: 4(1/6) см2.
VI. Самостоятельная работа
Учитель раздаёт карточки с заданиями двух уровней сложности.
Карточка. Уровень А
1) Две стороны треугольника равны 12 см и 9 см, угол между ними 30°. Найдите площадь треугольника. (Ответ: 27 см2)
2) AO = 4, BO = 9, CO = 5, DO = 8, SAOC = 15, SDOB = ?
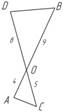
Рис. 18. Чертеж к условию задачи
(Ответ: 54 см2)
Уровень Б (для более подготовленных учащихся)
1) В треугольнике ABC ∠A = 45°, BC = 10 см, высота BD делит сторону AC на отрезки: AD = 6 см, DC = 8 см. Найдите площадь треугольника ABC и высоту, проведённую к стороне BC.
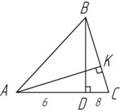
Рис. 19. Чертеж к условию задачи
Ответ: 42 см2; 8,4 см.
2)
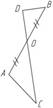
Рис. 20. Чертеж к условию задачи
OB = OA, OC = 2 • OD, SAOC = 12 см2, SBOD = ?
Ответ: 6 см2.
VII. Подведение итогов
Учитель оценивает работу учащихся.
VIII. Домашнее задание
1)
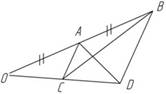
Рис. 21. Чертеж к условию задачи
Дано: AO = AB, прямая AC параллельна прямой BD.
Доказать: SAOD = SCOB
2)
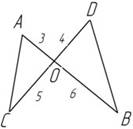
Рис. 22. Чертеж к условию задачи
Дано: AO = 3 см, BO = 6 см, CO = 5 см, DO = 4 см.
SAOC + SBOD = 39 см2.
Найти: SAOC = ?
Ответ 15 см2.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.