Теоретические дополнения к программе по физике для ЦТО по теме «Термодинамика»

 

 

 

 

Теоретические

дополнения

к программе

по физике

для ЦТО по теме «Термодинамика»

 

 

 

 

 

 

МКТ И ТЕРМОДИНАМИКА

§7. Теплоемкости газов

Для школьного курса физики (как впрочем и для ЕГЭ), возможно, данная тема и не нужна, но при решении олимпиадных заданий часто встречаются понятия теплоемкостей. Рассмотрим некоторые понятия (давайте применительно к газам):

Теплоемкость газа – физическая величина, равная энергии, которую нужно сообщить газу (или отвести от газа), чтобы изменить его температуру на 1К.

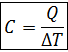
Единицы измерения - 1

Теплоемкость характеризует газ (или тело) в целом, т.е. это величина характеризующая данную массу газа.

Удельная теплоемкость газа – физическая величина, равная энергии, которую нужно сообщить газу (или отвести от газа) массой 1кг , чтобы изменить его температуру на 1К.

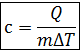
Единицы измерения - 1

Молярная теплоемкость газа – физическая величина, равная энергии, которую нужно сообщить газу (или отвести от газа) в количестве 1моль , чтобы изменить его температуру на 1К.

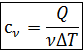
Единицы измерения - 1

Исходя из определений молярной и удельной теплоемкостей имеем:

Приравнивая правые части получим после сокращений:

ν

Так как    получаем

Последняя формула и выражает связь между удельной и молярной теплоемкостями.

В отличии от твердых тел и жидкостей, у газов следует различать, например, удельную теплоемкость при постоянном объёме  и при постоянном давлении . Получим выражения для каждой из этих величин. Для этого воспользуемся следующими формулами

  – первый закон термодинамики,

  – внутренняя энергия газа (i– число степеней свободы молекулы),

 – работа газа.

Рассмотрим каждый процесс подробнее.

1. Изохорический процесс. В данном процессе ∆V=0, следовательно, А=0, значит

С другой стороны . Приравнивая последние уравнения, после сокращения, получим выражение для удельной теплоемкости газа при постоянном объёме:

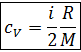
2. Изобарический процесс. В данном процессе ∆p=0, следовательно

С другой стороны

.

Приравнивая последние уравнения, после сокращения, получим выражение для удельной теплоемкости газа при постоянном давлении:

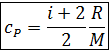
Получив выражения для удельных теплоемкостей, запишем и формулу Майера для показателя адиабаты в уравнении Пуассона:

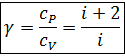
§ 8. Термодинамические циклы

Среди возможных термодинамических процессов, изучаемых в школьном курсе физики, особое место занимают процессы, соответствующие замкнутым кривым (рис.1). В этих процессах система проходит через ряд термодинамических состояний и возвращается в исходное. Такие процессы называют циклами.

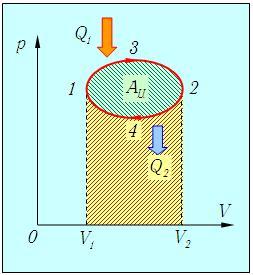
Рис. 1. Пример условного замкнутого цикла (направление процесса показано стрелками).

 

 

 

 

 

 

 Следует отметить некоторую особенность работы. Площадь под верхней кривой равна работе, совершаемой системой, а площадь под нижней кривой — работе внешних сил над системой (показана коричневой штриховкой). Разность площадей (показана зеленой штриховкой) равна полной работе, совершенной системой за цикл. В этом и состоит геометрический смысл работы, но следует помнить, что это верно только в осях pV.

Рассмотрим подробнее процесс на рис. 1. При расширении газа по «пути» 1-3-2 от минимального (V₁) до максимального (V₂) объема система совершает положительную работу А₁₃₂, численно равную площади под верхней кривой. При возвращении системы в исходное состояние по другому пути 2-4-1 paбота А₂₄₁ совершается над системой. Работа системы отрицательна и по абсолютной величине равна площади под нижней кривой. Алгебраическая сумма этих работ

есть полная работа, совершенная системой за цикл. Ее численная величина равна разности упомянутых площадей, то есть площади, заключенной между верхней и нижней кривыми. Иными словами, полная работа за цикл равна площади, ограниченной данным циклом на диаграмме (р, V), если процесс совершается по часовой стрелке; в противном случае полная работа отрицательна, но ее модуль также равен этой площади.

 В ходе осуществления цикла система взаимодействовала с внешней средой, получала и отдавала теплоту. Если обозначить через Q₁ количество теплоты, полученное системой, то коэффициент полезного действия 𝛈 естественно определить, как отношение

где А_Ц — работа за цикл.

КПД часто выражают также в процентах, для чего величину η надо умножить на 100 %. Если обозначить через Q₂ > 0 количество теплоты, возвращенное системой во внешнюю среду, то разность Q₁ – Q₂ равна совершенной работе А_Ц. Это следует из первого начала термодинамики и из того факта, что при возвращении системы в исходное состояние ее внутренняя энергия также принимает исходное значение, то есть

Тогда КПД тепловой машины записывается в виде

Отсюда видно, что КПД тепловой машины не может быть больше единицы. Это утверждение можно сформулировать как невозможность вечного двигателя первого рода:

Существование такого двигателя противоречило бы закону сохранения энергии. Поскольку ни количество теплоты, ни совершенная системой работа не являются функциями состояния, КПД зависит от данного конкретного цикла, по которому работает тепловая машина.

Мы рассмотрели процесс, соответствующий работе именно тепловой машины. Если повернуть процесс вспять (пустить его против часовой стрелки на рис. 1), то мы получим модель холодильной установки. Все стрелки на этом рисунке меняют направления на обратные, система получает от холодильника количество теплоты Q₂, и за счет работы внешней силы (электромотора) передает нагревателю большее количество теплоты Q₁. Закон сохранения энергии (первое начало термодинамики) требует выполнения равенства

Эффективность холодильной установки можно определить аналогично КПД тепловой машины. Надо только учесть, что полезным теперь является количество отнимаемого тепла Q₂, для чего мы совершаем работу А_Ц. Поэтому в литературе часто определяют холодильный коэффициент ’ как отношение отнимаемой теплоты к совершаемой при этом работе:

Заметим, что холодильный коэффициент может быть больше единицы. Если мы хотим пользоваться привычным коэффициентом полезного действия, то для холодильной установки естественно определить его как отношение отнятого тепла к переданному во внешнюю среду:

                          (4)

Такое определение соответствует традиционным взглядам на КПД установок. Действительно, в холодильнике со 100 %-й эффективностью (если бы он был возможен) все количество отнятой теплоты передавалось бы без совершения работы во внешнюю среду. Тогда мы имели бы Q₂ = Q₁ и _хол = 1. Наоборот, когда мы совершаем какую-то работу, но не отнимаем никакой теплоты, то Q₂ = 0 и _хол = 0.

 Цикл Карно

Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Т_mах, и холодильник, находящийся при температуре T_min (T_min < Т_mах). Предполагается, что при контакте с нашей системой температуры нагревателя и холодильника не меняются. При контакте с нагревателем система получает тепло, при контакте с холодильником - отдает его.

В термодинамике существует теорема Карно:

Рассмотрим круговой процесс, состоящий из двух изотерм и двух адиабат. Он и называется циклом Карно (рис. 1.).

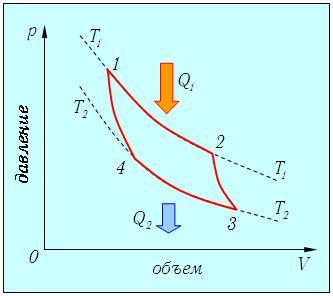
Изотерма 1-2. На этом участке газ находится в контакте с нагревателем и происходит изотермическое расширение от объема V₁ до объема V₂. Температура Т₁ не меняется, следовательно, не изменяется внутренняя энергия, а вся полученная теплота расходуется на совершение газом работы:

Q₁=Q₁₂=A₁₂

Величину работы газа при изотермическом процессе можно вычислить по  формуле

Тогда

Адиабата 2-3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q₂₃ = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т₂. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:

Изотерма 3-4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А₃₄ < 0), а выделяющееся тепло

передается холодильнику. Имеем аналогично (5.6)

Адиабата 4-1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т₁. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):

Из уравнений (2) и (4) находим отношения объемов

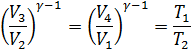
откуда следует, что

               (5)

Поэтому отдаваемую холодильнику теплоту Q₂ (см. уравнение (5.8)) можно записать как

Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу

 

Из проведенного анализа следует также, что максимальная температура в цикле равна Т_mах = Т₁, а минимальная — Т_min = Т₂. Если разделить (5) на (6), то немедленно получим выражение для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.

Задача. Идеальная тепловая машина с КПД η работает по обратному циклу (рис. 13.15). Какое максимальное количество теплоты можно забрать от холодильника, совершив механическую работу А?

Сразу отметим что в условии дан КПД тепловой машины, поэтому не стоит обращать внимание на слово холодильник.

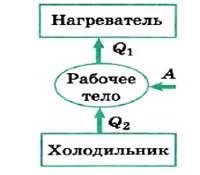Р е ш е н и е. Поскольку холодильная машина работает по обратному циклу, то для перехода тепла от менее нагретого тела к более нагретому необходимо, чтобы внешние силы совершили положительную работу. Принципиальная схема холодильной машины: от холодильника отбирается количество теплоты Q₂, внешними силами совершается работа и нагревателю передаётся количество теплоты Q₁. Следовательно,

 Cледовательно

₂₁,

 

Окончательно

Задача.  Идеальная холодильная машина, работающая по обратному циклу Карно, передает тепло от холодильника с водой при температуре t₂ = 0°С кипятильнику с водой при температуре t₁ = 100 °C. Какую массу m₂ воды нужно заморозить в холодильнике, чтобы превратить в пар массу m₁ = 1 кг воды в кипятильнике?

Решение: Коэффициент холодильной машины:

Энергия, отданная холодильнику: Q₂=λm₂

Энергия, переданная кипятильнику: Q₁=Lm₁

Иначе

Или    ηQ₁-𝜂Q₂=Q₂, следовательно,

Значит

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§ 9. Влажность

Задача №1 (ДВИ МГУ 2018)

Определить массу воды m, которую теряет человек за τ=1 ч в процессе дыхания, исходя из следующих данных. Относительная влажность вдыхаемого воздуха φ₁ = 60%, относительная влажность выдыхаемого воздуха φ₂ =100%. Человек делает в среднем n=15 вдохов в минуту, вдыхая каждый раз V =2,5 л воздуха. Температуру вдыхаемого и выдыхаемого воздуха принять t = 36^◦C; давление насыщенного водяного пара при этой температуре p_H = 59 кПа. Молярная масса воды M =18 г/моль, универсальная газовая постоянная R=8,3 Дж(моль·К).

Дано:                                                     Решение:

τ=3600с       

n=15

t=60c.

V =2,5_*10^-3м³

 φ₁ = 0,6

φ₂ =1

Т=309К.

p_H = 59_*10³Па                            

M =18_*10^-3 кг/моль                     

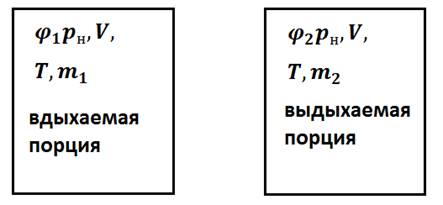
m - ?                                            Изобразим на рисунке обе порции воздуха (вдыхаемую и выдыхаемую), указав основные термодинамические параметры. Из уравнения Менделеева-Клапейрона следует:

Тогда за один вдох потеряется масса:

Число вдохов:

Значит искомая масса:

Ответ: 37г.

Задача №2. (Сборник задач "Отличник ЕГЭ")

В вертикальном цилиндре, наполовину заполненном водой, под подвижным поршнем заключен воздух. Поршень находится в равновесии, когда давление внутри цилиндра равно утроенному атмосферному давлению. При температуре t₁ = 6^◦C расстояние между поршнем и поверхностью воды h = 10 см. На каком расстоянии H от поверхности воды окажется поршень, если цилиндр нагреть до температуры t₂ = 100^◦C? Атмосферное давление считать нормальным. Давлением водяных паров при температуре (t₁ = 6^◦C и изменением объема воды за счет се испарения и теплового расширения пренебречь.

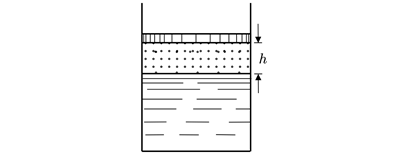
Решение: Расставим силы, действующие на поршень в процессе движения

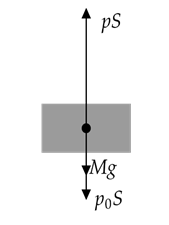Здесь p – давление влажного воздуха, M – масса поршня.

Запишем второй закон Ньютона:

где F = pS – сила, с которой газ давит на поршень давления газа, F₀ = p₀S – сила давления атмосферы, a – ускорение поршня.

В состоянии покоя a = 0. Спроецируем второй закон Ньютона в вертикальную ось:

Отсюда

Так как по условию , получим

По условию давлением насыщенных паров при температуре t₁ = 6^◦C пренебрежимо мало, поэтому давление сухого воздуха p₁ = 3p₀. При температуре t₂ = 100^◦C давление насыщенных паров становится равным атмосферному . Следовательно, давление сухого воздуха при этой температуре

Таким образом для сухого воздуха имеем:

Состояние 1:

Состояние 2:

Применяя уравнение Клапейрона получаем

Отсюда

Ответ: 20 см.

Задача 3. («Покори Воробьёвы горы!», 2014, 10–11).

В гладкой горизонтальной трубе, закрытой с одного конца, находятся два вертикальных поршня (см. рисунок). Поршень 1 можно передвигать по трубе, фиксируя в разных положениях. Поршень 2 свободно скользит в трубе. Объём между поршнями вакуумирован, и между ними вставлена невесомая пружина. Между поршнем 2 и закрытым торцом трубы находится воздух с относительной влажностью φ = 40%. Первоначально поршень 1 находится от торца трубы на расстоянии, равном длине недеформированной пружины, а поршень 2 – на расстоянии x₀ = 5 см. Температура системы поддерживается постоянной. Известно, что при заполнении объёма между поршнем 2 и торцом трубы только насыщенным водяным паром при этой же температуре поршень 2 (при том же положении поршня 1) располагался на расстоянии x₀/2 от торца. На какое расстояние надо сдвинуть поршень 1, чтобы расстояние между поршнем 2 и торцом трубы уменьшилось в n = 4 раза? Ответ приведите в см, округлив до десятых

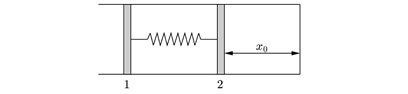
Решение:

Пусть L₀ – длина недеформированной пружины, p₀ – давление насыщенных паров, p_в – давление воздуха.

Для первого состояния kx₀ = (φp₀+ p_в)S, для второго состояния, откуда p_в = 1,6p₀.

В конце давление водяных паров будет равно давлению насыщенных паров p₀, а давление воздуха 4p_в, откуда

Тогда  см

Задача №7. ( ДВИ МГУ 2018)

В цилиндре под поршнем при температуре 20^◦C находятся воздух, водяные пары и вода. Число молей воздуха равно числу молей пара, а масса воды в три раза больше массы пара. Объём смеси медленно увеличивают при постоянной температуре до тех пор, пока относительная влажность воздуха не уменьшится до 50%. Определите конечное давление влажного воздуха p, если давление насыщенного пара при 20^◦C равен p_нас = 2,33 кПа

Решение:

Поскольку в начальном состоянии пар в цилиндре является насыщенным, и число молей воздуха равно числу молей пара, то парциальное давление сухого воздуха в этом состоянии равно  . Пусть масса пара равна m, тогда масса вода 3m. Пар массой m занимает объём V. В сосуде общее количество воды (в любом состоянии) 4m, следовательно, при медленном расширении смеси в 4 раза вся вода испарится, а пар останется насыщенным, т.е. относительная влажность воздуха сохранится равной 100%. Для того чтобы относительная влажность воздуха уменьшилась до 50%, нужно увеличить объем смеси еще в два раза. Таким образом, конечный объем смеси равен восьми начальным объемам. Следовательно, конечное давление сухого воздуха уменьшится в 8 раз, а давление пара уменьшится в 2 раза по сравнению с начальными значениями.

Искомое конечное давление влажного воздуха

Ответ: 1,46 кПа

Задача №10. (Ломоносов 2013)

 В сосуде находился влажный воздух. При изотермическом сжатии его объем уменьшился в 5 раз, а давление увеличилось в 3 раза. При дальнейшем изотермическом сжатии в 3 раза давление в итоге стало в 7 раз больше первоначального. Какую относительную влажность φ имел воздух до начала сжатия?

Решение: в начальном состоянии давление в сосуде (по закону Дальтона):

При первом сжатии в 5 раз давление смеси сухого воздуха и водяного пара в сосуде возросло в 3 раза, поэтому пар стал насыщенным и частично сконденсировался. Значит давление сухого воздуха возросло в 5 раз, а давление пара стало равно давлению насыщенного пара:

С другой стороны (т.к. давление возросло в 3 раза)

Приравнивая выражения (1) и (2) и приводя подобные, получим:

 При дальнейшем сжатии давление пара p_н уже не менялось. Пренебрежем объемом сконденсировавшейся воды. Парциальное давление сухого воздуха при первом сжатии возросло в 5 раз, а при втором – еще в 3 раза. В итоге возросло в 15 раз. Значит:

А с другой стороны в 7 раз больше первоначального:

Аналогично из (4) и (5), следует:

Умножим уравнение (3) на 4 и приравняем правые части:

Ответ: 60%