
4.1. Опорный план и его свойства
Рассмотрим каноническую задачу линейного программирования, записанную в векторно-матричной форме
![]() (4.1)
(4.1)
![]() ,
, ![]() ,
(4.2)
,
(4.2)
![]() .
(4.3)
.
(4.3)
Будем в дальнейшем считать, что ранг матрицы А системы
уравнений ![]() равен m (r(A) = m). m < n.
равен m (r(A) = m). m < n.
Рассмотрим ограничение (4.2). Пусть m < n (при m = n задача (4.1) - (4.3) имеет единственное решение и с точки зрения выбора оптимального решения из нескольких альтернативных вариантов интереса не представляет).
В случае m < n ЗЛП имеет множество решений. Кроме того, из линейной алгебры известно, что в этом случае любые m переменных могут быть выражены через остальные (n - m) переменные путем эквивалентных преобразований, т.е. переменные могут представлены как линейные функции остальных переменных.
Определение 4.1. Форма записи ЗЛП при наличии системы m линейно независимых ограничений задачи с n переменными, в которой m переменных выражены через остальные (n - m) переменные, называется ее базисным видом.
Определение 4.2. Переменные, представленные в базисном виде ЗЛП в качестве функций, называются базисными. Остальные переменные, представляющие собой аргументы базисных переменных, называются свободными переменными.
Определение 4.3. Решение задачи ЛП, в котором все свободные переменные равны нулю и, следовательно, базисные переменные равны свободным членам, называется базисным.
Определение 4.4. Базисное решение, в котором все базисные переменные неотрицательны, является допустимым (так как по условию задачи ее переменные являются неотрицательными).
Для задачи ЛП, содержащей ограничения, представляющие систему m
линейно независимых уравнений с n переменными, можно получить ![]() базисных решений, среди которых
могут быть допустимые и недопустимые решения.
базисных решений, среди которых
могут быть допустимые и недопустимые решения.
Запишем КЗЛП в векторной форме:
![]() (4.4)
(4.4)
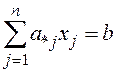 ,
(4.5)
,
(4.5)
![]() ,
,![]() ,
(4.6)
,
(4.6)
где ![]() -
j-й столбец матрицы А.
-
j-й столбец матрицы А.
Определение 4.4. Опорным планом (ОП) задачи линейного программирования
будем называть такой ее план, который является базисным решением системы
линейных уравнений ![]() . Согласно определению и предположению о том, что r(A) = m, всякому опорному
плану задачи линейного программирования (как и всякому базисному решению
системы линейных уравнений
. Согласно определению и предположению о том, что r(A) = m, всякому опорному
плану задачи линейного программирования (как и всякому базисному решению
системы линейных уравнений ![]() ) соответствует
базисная подматрица В порядка m
матрицы А и определенный набор m
базисных переменных системы линейных уравнений
) соответствует
базисная подматрица В порядка m
матрицы А и определенный набор m
базисных переменных системы линейных уравнений ![]() .
.
Определение 4.5. m компонент
базисного решения системы линейных уравнений ![]() ,
являющихся значениями соответствующих ему базисных переменных, будем называть
базисными компонентами этого опорного плана. Отметим, что базисные компоненты
опорного плана неотрицательны, а остальные (n-m) его компонент равны нулю. Очевидно, что число опорных
планов задачи линейного программирования конечно и не превышает
,
являющихся значениями соответствующих ему базисных переменных, будем называть
базисными компонентами этого опорного плана. Отметим, что базисные компоненты
опорного плана неотрицательны, а остальные (n-m) его компонент равны нулю. Очевидно, что число опорных
планов задачи линейного программирования конечно и не превышает ![]() . Число строго положительных
компонент опорного плана не превышает m.
. Число строго положительных
компонент опорного плана не превышает m.
Определение 4.6. К-матрицей КЗЛП будем называть расширенную
матрицу системы линейных уравнений, равносильной системе 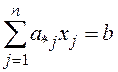 , содержащую единичную
подматрицу на месте первых n своих столбцов и все элементы ( n+1 )-го
столбца которой неотрицательны.
, содержащую единичную
подматрицу на месте первых n своих столбцов и все элементы ( n+1 )-го
столбца которой неотрицательны.
Число
К-матриц конечно и не превышает ![]() . Каждая
К-матрица определяет ОП КЗЛП и наоборот.
. Каждая
К-матрица определяет ОП КЗЛП и наоборот.
4.2. Геометричесая интерпретация опорных планов. Существование оптимальных опорных планов
Остановимся сначала на рассмотрении вопроса о связи допустимых базисных решений (опорных планов) ЗЛП и вершин допустимого многогранника. Покажем, что допустимые базисные решения и вершины допустимого многогранника - суть одно и тоже. Этот факт устанавливает следующая теорема.
Теорема 4.1. Для того, чтобы точка ![]() была
вершиной множества допустимых решений (вершиной допустимого многогранника)
задачи (4.4) - (4.6), необходимо и достаточно, чтобы векторы условий
была
вершиной множества допустимых решений (вершиной допустимого многогранника)
задачи (4.4) - (4.6), необходимо и достаточно, чтобы векторы условий ![]() , отвечающие ее положительным
координатам, были линейно независимы. Доказательство теоремы приведено,
например, в [7].
, отвечающие ее положительным
координатам, были линейно независимы. Доказательство теоремы приведено,
например, в [7].
Существование базисных оптимальных решений устанавливает следующая теорема.
Теорема 4.2. Среди оптимальных решений любой задачи (4.4) - (4.6) всегда найдется хотя бы одна вершина допустимого многогранника. Доказательство теоремы также приведено, например, в [7].
Оптимальность допустимых базисных решений можно установить на основе принципа оптимальности, который для задачи (4.4) - (4.6) заключается в том, что в выражении целевой функции, записанном через свободные переменные, все коэффициенты при таких переменных либо меньше, либо равны нулю.
Действительно, при максимизации целевой функции в случае, если коэффициенты при свободных переменных в ее выражении меньше либо равны нулю, то базисное решение (свободные переменные равны нулю) доставляет максимум целевой функции по всему возможному набору свободных переменных (которые не могут быть отрицательными).
Таким образом, утверждение теоремы 4.2 позволяет организовать поиск
оптимального решения ЗЛП. Поскольку вершин допустимого многогранника может быть
не более чем ![]() и среди них есть оптимальное
решение задачи, то поиск этих вершин и определение среди них оптимального
решения требует конечного числа арифметических операций и может быть названо
конечным алгоритмом решения ЗЛП.
и среди них есть оптимальное
решение задачи, то поиск этих вершин и определение среди них оптимального
решения требует конечного числа арифметических операций и может быть названо
конечным алгоритмом решения ЗЛП.
Однако говорить о таком алгоритме всерьез не приходиться, поскольку
величина ![]() становится астрономически большой
даже при небольших значениях n и m. Здесь нужен упорядоченный перебор допустимых базисных
решений.
становится астрономически большой
даже при небольших значениях n и m. Здесь нужен упорядоченный перебор допустимых базисных
решений.
Покажем это на примерах решения ЗЛП.
4.3. Решение задач линейного программирования на основе
сформулированных свойств
В качестве примера рассмотрим ЗЛП из второй главы (2.28) - (2.30):
![]() ,
,
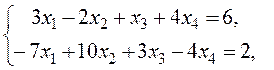
![]() ,
, ![]() .
.
Сначала приведём условия задачи к базисному виду, выполнив преобразования с использованием метода Жордана-Гаусса как и во второй главе. Результаты представлены в табл. 2.1.
Используя данные из табл. 2.1 запишем базисный вид ЗЛП:
![]()
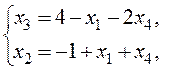
Базисными переменными являются переменные ![]() ,
а свободными
,
а свободными ![]() . Приравнивая свободные переменые к
«0», получим следующее базисное решение:
. Приравнивая свободные переменые к
«0», получим следующее базисное решение: ![]() .
Т.к. в полученном базисном решении переменная
.
Т.к. в полученном базисном решении переменная ![]() ,
то данное базисное решение не является допустимым и не соответствует вершине
допустимого многогранника ЗЛП.
,
то данное базисное решение не является допустимым и не соответствует вершине
допустимого многогранника ЗЛП.
Выберем теперь для преобразований в качестве базисных переменные ![]() . Результаты представлены в табл.
4.1.
. Результаты представлены в табл.
4.1.
Используя данные из табл. 4.1 запишем базисный вид ЗЛП:
![]()
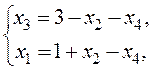
Приравнивая свободные переменые к «0», получим следующее базисное
решение: ![]() . Т.к. в полученном базисном
решении все переменные не отрицательны, то данное базисное решение является допустимым
и соответствует вершине допустимого многогранника ЗЛП.
. Т.к. в полученном базисном
решении все переменные не отрицательны, то данное базисное решение является допустимым
и соответствует вершине допустимого многогранника ЗЛП.
Рассмотрим полученное уравнение для целевой функции. Коэффициенты при свободных переменных отрицательны (-2 и –3), т.е. полученное базисное решение является оптимальным. Оптимальное значение целевой функции равно 7.
Таблица 4.1
|
|
|
|
|
|
|
Действия |
|
ограничение |
3 |
-2 |
1 |
4 |
6 |
|
|
ограничение |
-7 |
10 |
3 |
-4 |
2 |
´(-3) и сложить со 2-й строкой |
|
|
4 |
-5 |
1 |
2 |
0 |
´(-1) и сложить с 3-й строкой |
|
Результаты первого шага |
||||||
|
Первое ограничение |
3 |
-2 |
1 |
4 |
6 |
|
|
Второе ограничение |
-16 |
16 |
0 |
-16 |
-16 |
´(-1/16) |
|
Целевая функция |
1 |
-3 |
0 |
-2 |
-6 |
|
|
Результаты второго шага |
||||||
|
ограничение |
3 |
-2 |
1 |
4 |
6 |
´(-3) и сложить с 1-й строкой |
|
ограничение |
1 |
-1 |
0 |
1 |
1 |
|
|
Целевая функция |
1 |
-3 |
0 |
-2 |
-6 |
´(-1) и сложить с 3-й строкой |
|
Результаты третьего шага |
||||||
|
Первое ограничение |
0 |
1 |
1 |
1 |
3 |
|
|
Второе ограничение |
1 |
-1 |
0 |
1 |
1 |
|
|
Целевая функция |
0 |
-2 |
0 |
-3 |
-7 |
|
4.4. Требования к алгоритму численного метода решения задач линейного программирования
Пусть требуется решить задачу (4.4) - (4.6). Так как по доказанному выше
решением этой задачи является неотрицательное базисное решение системы линейных
уравнений ![]() , то метод её решения должен
содержать четыре момента:
, то метод её решения должен
содержать четыре момента:
1) обоснование способа перехода от одного опорного плана (К-матрицы) к другому;
2) указание признака оптимальности, позволяющего проверить, является ли данный опорный план оптимальным;
3) указание способа построения нового опорного плана, более близкого к оптимальному;
4) указание признака отсутствия конечного решения.
4.5. Задачи и упражнения
4.5.1. Для КЗЛП, полученной в п. 2.5.2, определить два базисных решения. Сделать выводы о их допустимости и оптимальности.
4.5.2. Задачу из п. 2.5.3 записать в базисном виде, определить для него базисное решение и сделать выводы о его допустимости и оптимальности.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.