
Теория
Үшбұрышқа іштей сызылған шеңбер – Вписанная в треугольник окружность – Inscribed circle of a triangle
Биссектриса – Биссектриса – Bisector
Үшбұрышқа сырттай сызылған шеңбер – Описанная окружность треугольника – Circumscribed circle of a triangle
Орта перпендикуляр – Серединный перпендикуляр – Middle perpendicular
|
Үшбұрышқа іштей сызылған шеңбер Үшбұрыштың барлық қабырғаларын жанайтын шеңбер үшбұрышқа іштей сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың биссекрисаларының қиылысу нүктесіне, ал радиусы осы центрден үшбұрыш қабырғасына түсірілген перпендикулярдың ұзындығына тең. Теорема. Үшбұрышқа іштей сызылған шеңберлер центрі үшбұрыштың биссектрисаларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына іштей сызылған шеңбер центрі О, ал қабырғаларымен жанасу нүктелері F, Nжәне M болсын (суретте). ОF = OM (шеңбер радиустары) және АО гипотенузасы ортақ болғандықтан, ∆AOM = ∆AOF. Онда ∠ОАМ= ∠ОАE, яғни үшбұрышқа іштей сызылған шеңбер центрі О нүктесі Оа биссектрисасында жатыр. Осы сияқты О нүктесін үшбұрыштың өзге биссектрисаларында жататынын көрсетуге болады. Теорема дәлелденді |
|
|
Үшбұрышқа сырттай сызылған шеңбер Үшбұрыштың барлық төбелері арқылы өтетін шеңбер сол үшбұрышқа сырттай сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың орта перпендикулярларының қиылысу нүктесі. Теорема. Үшбұрышқа сырттай сызылған шеңбердің центрі ұшбұрыштың орта перпендикулярларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына центрі О болатын сырттай шеңбер сызылған. Онда АВС үшбұрышының қабырғалары осы шеңбердің хордалары болады. Хорданың ортасы арқылы өтетін диаметр хордаға перпендикулярлығы теоремасы бойынша үшбұрыш қабырғаларының орта перпендикулярлары шеңбер диаметрінде жатады, яғни шеңбердің центрі арқылы өтеді. Теорема дәлелденді. |
|
________________________________________________________________________________________
Теория
Үшбұрышқа іштей сызылған шеңбер – Вписанная в треугольник окружность – Inscribed circle of a triangle
Биссектриса – Биссектриса – Bisector
Үшбұрышқа сырттай сызылған шеңбер – Описанная окружность треугольника – Circumscribed circle of a triangle
Орта перпендикуляр – Серединный перпендикуляр – Middle perpendicular
|
Үшбұрышқа іштей сызылған шеңбер Үшбұрыштың барлық қабырғаларын жанайтын шеңбер үшбұрышқа іштей сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың биссекрисаларының қиылысу нүктесіне, ал радиусы осы центрден үшбұрыш қабырғасына түсірілген перпендикулярдың ұзындығына тең. Теорема. Үшбұрышқа іштей сызылған шеңберлер центрі үшбұрыштың биссектрисаларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына іштей сызылған шеңбер центрі О, ал қабырғаларымен жанасу нүктелері F, Nжәне M болсын (суретте). ОF = OM (шеңбер радиустары) және АО гипотенузасы ортақ болғандықтан, ∆AOM = ∆AOF. Онда ∠ОАМ= ∠ОАE, яғни үшбұрышқа іштей сызылған шеңбер центрі О нүктесі Оа биссектрисасында жатыр. Осы сияқты О нүктесін үшбұрыштың өзге биссектрисаларында жататынын көрсетуге болады. Теорема дәлелденді |
|
|
Үшбұрышқа сырттай сызылған шеңбер Үшбұрыштың барлық төбелері арқылы өтетін шеңбер сол үшбұрышқа сырттай сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың орта перпендикулярларының қиылысу нүктесі. Теорема. Үшбұрышқа сырттай сызылған шеңбердің центрі ұшбұрыштың орта перпендикулярларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына центрі О болатын сырттай шеңбер сызылған. Онда АВС үшбұрышының қабырғалары осы шеңбердің хордалары болады. Хорданың ортасы арқылы өтетін диаметр хордаға перпендикулярлығы теоремасы бойынша үшбұрыш қабырғаларының орта перпендикулярлары шеңбер диаметрінде жатады, яғни шеңбердің центрі арқылы өтеді. Теорема дәлелденді. |
|
Теория
Үшбұрышқа іштей сызылған шеңбер – Вписанная в треугольник окружность – Inscribed circle of a triangle
Биссектриса – Биссектриса – Bisector
Үшбұрышқа сырттай сызылған шеңбер – Описанная окружность треугольника – Circumscribed circle of a triangle
Орта перпендикуляр – Серединный перпендикуляр – Middle perpendicular
|
Үшбұрышқа іштей сызылған шеңбер Үшбұрыштың барлық қабырғаларын жанайтын шеңбер үшбұрышқа іштей сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың биссекрисаларының қиылысу нүктесіне, ал радиусы осы центрден үшбұрыш қабырғасына түсірілген перпендикулярдың ұзындығына тең. Теорема. Үшбұрышқа іштей сызылған шеңберлер центрі үшбұрыштың биссектрисаларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына іштей сызылған шеңбер центрі О, ал қабырғаларымен жанасу нүктелері F, Nжәне M болсын (суретте). ОF = OM (шеңбер радиустары) және АО гипотенузасы ортақ болғандықтан, ∆AOM = ∆AOF. Онда ∠ОАМ= ∠ОАE, яғни үшбұрышқа іштей сызылған шеңбер центрі О нүктесі Оа биссектрисасында жатыр. Осы сияқты О нүктесін үшбұрыштың өзге биссектрисаларында жататынын көрсетуге болады. Теорема дәлелденді |
|
|
Үшбұрышқа сырттай сызылған шеңбер Үшбұрыштың барлық төбелері арқылы өтетін шеңбер сол үшбұрышқа сырттай сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың орта перпендикулярларының қиылысу нүктесі. Теорема. Үшбұрышқа сырттай сызылған шеңбердің центрі ұшбұрыштың орта перпендикулярларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына центрі О болатын сырттай шеңбер сызылған. Онда АВС үшбұрышының қабырғалары осы шеңбердің хордалары болады. Хорданың ортасы арқылы өтетін диаметр хордаға перпендикулярлығы теоремасы бойынша үшбұрыш қабырғаларының орта перпендикулярлары шеңбер диаметрінде жатады, яғни шеңбердің центрі арқылы өтеді. Теорема дәлелденді. |
|
________________________________________________________________________________________
Теория
Үшбұрышқа іштей сызылған шеңбер – Вписанная в треугольник окружность – Inscribed circle of a triangle
Биссектриса – Биссектриса – Bisector
Үшбұрышқа сырттай сызылған шеңбер – Описанная окружность треугольника – Circumscribed circle of a triangle
Орта перпендикуляр – Серединный перпендикуляр – Middle perpendicular
|
Үшбұрышқа іштей сызылған шеңбер Үшбұрыштың барлық қабырғаларын жанайтын шеңбер үшбұрышқа іштей сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың биссекрисаларының қиылысу нүктесіне, ал радиусы осы центрден үшбұрыш қабырғасына түсірілген перпендикулярдың ұзындығына тең. Теорема. Үшбұрышқа іштей сызылған шеңберлер центрі үшбұрыштың биссектрисаларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына іштей сызылған шеңбер центрі О, ал қабырғаларымен жанасу нүктелері F, Nжәне M болсын (суретте). ОF = OM (шеңбер радиустары) және АО гипотенузасы ортақ болғандықтан, ∆AOM = ∆AOF. Онда ∠ОАМ= ∠ОАE, яғни үшбұрышқа іштей сызылған шеңбер центрі О нүктесі Оа биссектрисасында жатыр. Осы сияқты О нүктесін үшбұрыштың өзге биссектрисаларында жататынын көрсетуге болады. Теорема дәлелденді |
|
|
Үшбұрышқа сырттай сызылған шеңбер Үшбұрыштың барлық төбелері арқылы өтетін шеңбер сол үшбұрышқа сырттай сызылған шеңбер деп аталады. Бұл шеңбердің центрі – үшбұрыштың орта перпендикулярларының қиылысу нүктесі. Теорема. Үшбұрышқа сырттай сызылған шеңбердің центрі ұшбұрыштың орта перпендикулярларының қиылысу нүктесі болады. Дәлелдеуі. АВС үшбұрышына центрі О болатын сырттай шеңбер сызылған. Онда АВС үшбұрышының қабырғалары осы шеңбердің хордалары болады. Хорданың ортасы арқылы өтетін диаметр хордаға перпендикулярлығы теоремасы бойынша үшбұрыш қабырғаларының орта перпендикулярлары шеңбер диаметрінде жатады, яғни шеңбердің центрі арқылы өтеді. Теорема дәлелденді. |
|
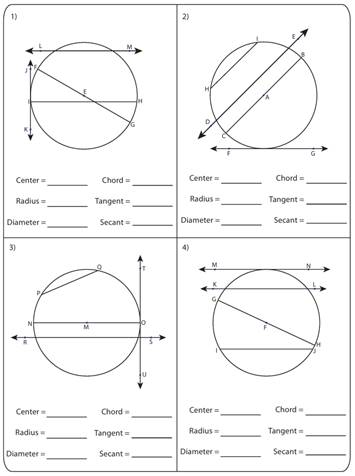

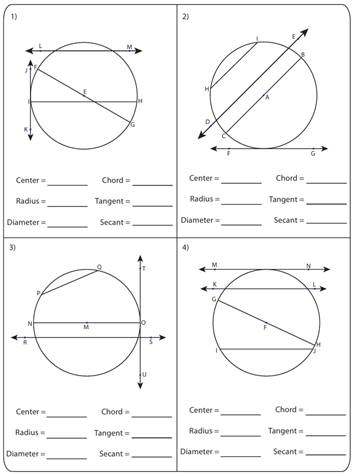
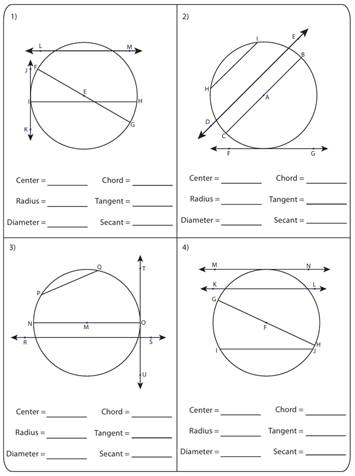
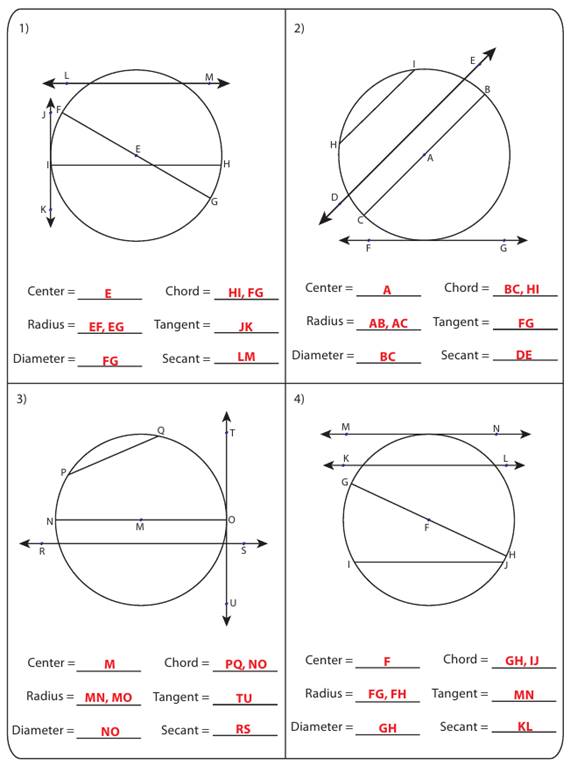
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.