ТЕОРИЯ И МЕТОДЫ РЕШЕНИЯ ЗАДАНИЯ 11 ЕГЭ

         Теоретический материал, необходимый для решения задания 11, довольно обширен.

1. Прежде всего необходимо повторить понятие и способы задания функции.

Если каждому элементу х из множества X, по определённому правилу ставится в соответствие определённое и единственное значение у из множества У, то такое соответствие называется функцией.

При этом  х называется независимой переменной или аргументом функции, а у -  зависимой переменной или значением функции.

Множество Х называют областью определения функции D(f), множество Y — областью значений функции E(f).

Основные способы задания функции:

- аналитический — с помощью формулы y = f(x);

- графический - множеством всех точек координатной плоскости с координатами (x;f(x));

также существуют табличный, словесный (описательный) и другие способы, которые в данном задании менее важны.

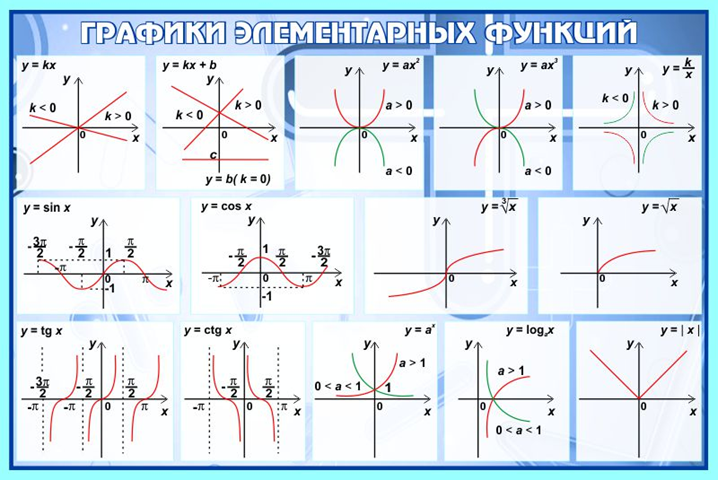
2. Для общего повторения изученных в школьном курсе математики видов функций, их свойств и графиков можно использовать стенды графиков элементарных функций:

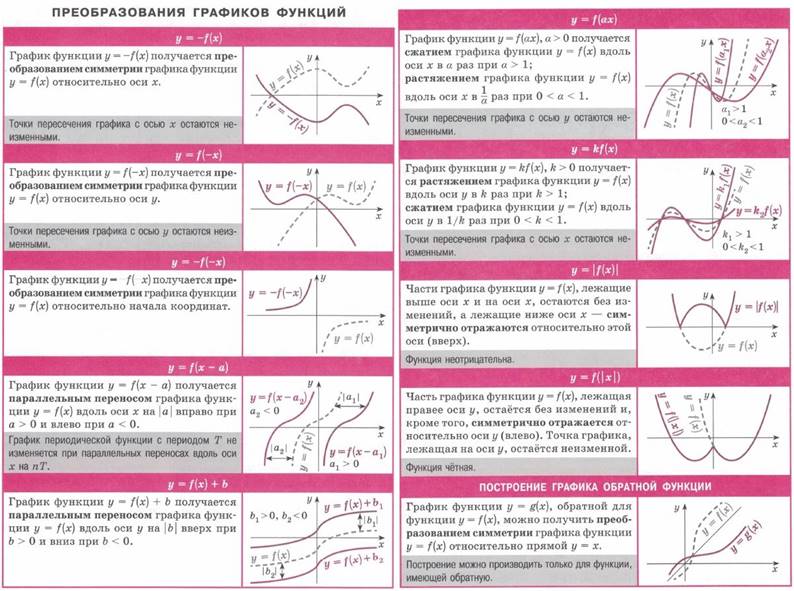
3. Основная часть заданий № 9 сводится к определению неизвестных коэффициентов формул, задающих функции, по частям изображенных графиков. Можно свести эти задачи к подстановке в формулы координат точек графика (определяются по рисунку) и решению систем уравнений. Это универсальный способ. Однако, часто задача значительно упрощается, если помнить правила преобразований графиков функций:

4. Необходимо также повторить связь между графиками функций и коэффициентами формул, которые их задают.

         Прежде всего, это относится к квадратичной функции. Полезно повторить оба вида её формул:

1) у=ах² + bх + с, где (0,с) — точка пересечения параболы с осью у,  а абсцисса вершины параболы вычисляется по формуле ,

2) у= а(х-хо)² + уо, где ( хо ; уо ) - координаты вершины параболы,

и в зависимости от ситуации задачи, применять ту формулу, которая «удобнее».

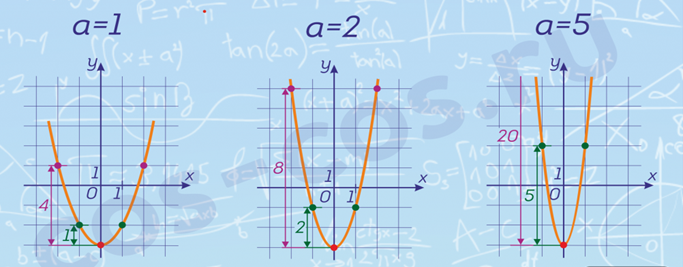
         Так же полезно вспомнить, как «по клеточкам» можно определить коэффициент а при  х². Например:

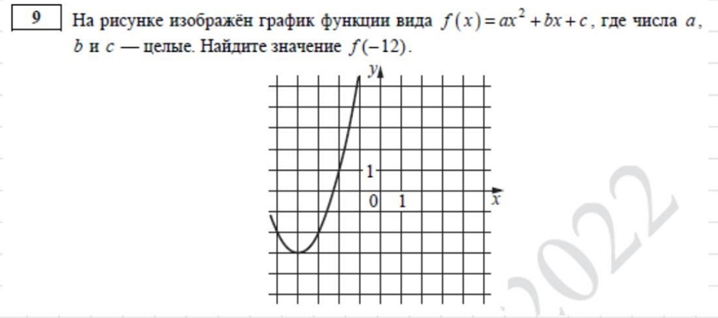
Рассмотрим для примера задание из демоверсии 2022 года:

Способ 1.

Выделяем на графике три точки с целочисленными координатами. Например:

 (-4;-3), (-3;-2), (-2;1).

Подставляя координаты точек в заданное уравнение, получаем систему из трех уравнений с тремя неизвестными:

   16a - 4b + c = -3

   9a - 3b + c = -2

   4a - 2b + c = 1

Далее, вычитая, например, из первого уравнения второе, и из второго третье, получим:

   7а - b = -1

   5a - b = -3 

Из новой системы, также методом вычитания получим 2а = 2 => а = 1.

После этого подстановкой значения а в любое уравнение второй системы получаем b = 8, и подстановкой значений а и b в любое уравнение первой системы с = 13.

Получили уравнение: f(x) = x² + 8х + 13.

Значит, f(-12) = (-12)² + 8(-12) + 13 = 61.

Способ 2.

Можно было начать решение с применения формулы абсциссы вершины параболы.   Получили бы:  -4 = , откуда  b = 8a => f(x) = ax² + 8aх +c

Далее, выбираем две точки на графике, например, опять  (-4;-3), (-3;-2).

Подставляя координаты точек в полученное уравнение, получаем систему из двух уравнений с двумя неизвестными:

   -16a + c = -3

   -15a + c = -2 , откуда а = 1 => в = 8, с = 13.

Получили уравнение: f(x) = x² + 8х + 13.

Значит, f(-12) = (-12)² + 8(-12) + 13 = 61.

Способ 3.

Определим по графику значение коэффициента а при x² . Для этого можно «перенести» вершину параболы в начало координат. Тогда очевидно, что одна из точек параболы будет иметь координаты (1;1), а уравнение заданной функции примет вид 

f(x) = ax². Подставляя координаты точки (1;1) в это уравнение, получим а = 1.

Далее воспользуемся формулой

f(x) = а(х-хо)² + уо, где ( хо ; уо ) - координаты вершины параболы.  Так как координаты вершины (-4;-3), получаем уравнение: f(x) = (х + 3)² - 4.     

Значит,  f(-12) = (-12 + 3)² - 4 =  61.

Ответ: 61

 Можно также комбинировать разные способы, и это относится к любым видам заданных в номере 9 функций. 

5.  Методы нахождения по графику коэффициентов уравнения линейной функции.

Общий вид линейной функции: у = kx + b, где k — угловой коэффициент, равный тангенсу угла наклона прямой к положительному направлению оси Х, а коэффициент b равен ординате точки пересечения графика с осью Y.

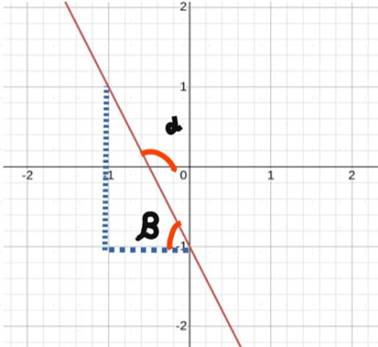
Рассмотрим график линейной функции y = kx + b:

Для составления уравнения этой функции можно:

Способ 1.

Подставить координаты точек (0;-1) и (-1;1) в уравнение  у = kx + b. Получим систему:

 -1 = b

 1 = -k + b, откуда  получаем : y = -2x - 1.

Способ 2.

Подставить  координаты выбранных точек (х1;у1) и ( х2;у2) в  каноническое уравнение прямой:

                                                       .

Получим:      , откуда -2(х+1) = у - 1  =>  y = -2x - 1.

Способ 3.

Определить угловой коэффициент k, как тангенс угла наклона прямой к положительному направлению оси Х: k = tg α = - tg β = -= - 2 , а коэффициент b как ординату точки пересечения графика с осью Y: b = -1. То есть  y = -2x - 1.

Можно также один из коэффициентов k или b найти по способу 3, а второй подстановкой координат выбранной точки.

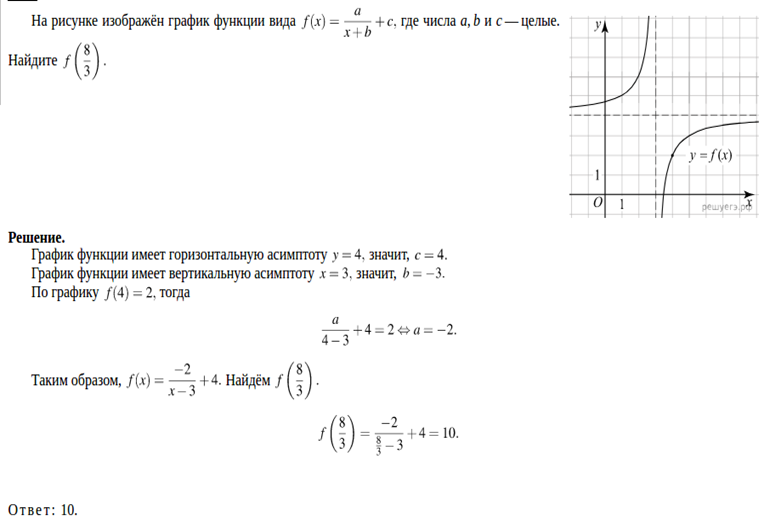
6.  В задачах с гиперболами наиболее удобен способ нахождения коэффициентов по правилам преобразования графиков функций. При этом перенос графика в направлении координатных осей мы можем увидеть по расположению его асимптот. Например:

7. Особую сложность вызывает у обучающихся поиск неизвестных коэффициентов тригонометрических функций. Здесь, кроме общих правил преобразований, помогут следующие:

если функция задана формулой у= а cos (kx) + b  (или  у= а sin (kx) + b), то:

1) ;   2);   3) , где Т — наименьший положительный период функции.

Например:

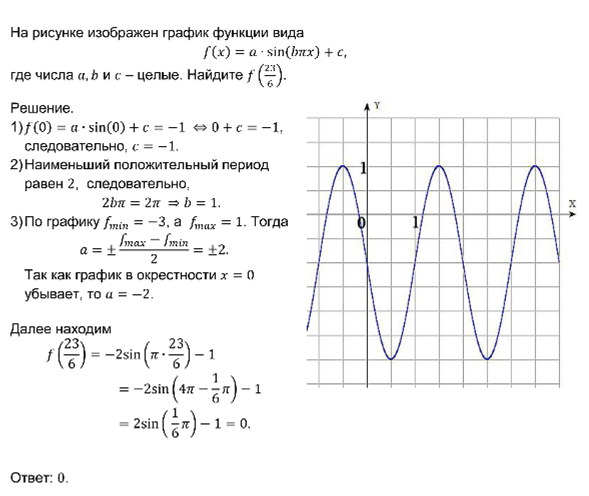
8. Для выполнения заданий на нахождение координат точки пересечения графиков двух функций у = f(x) и у = g(x), целесообразно напомнить, что абсциссы общих точек являются решениями уравнения f(x) = g(x).

Пример такого задания:

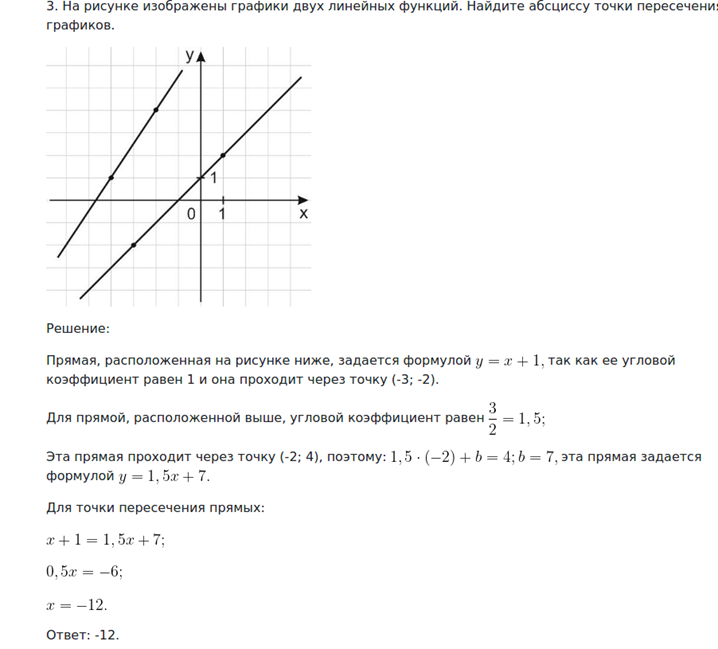
Для теоретической части использованы материалы:

https://dpva.ru/Guide/GuideMathematics/MathsForTheYoungest/MathShpargalka/  

http://cos-cos.ru/ege/zadacha203/378/  

https://www.mathm.ru/zad/ege/zad9eget.html#tema4

https://math-ege.sdamgia.ru/test?filter=all&category_id=125

Скачано с www.znanio.ru