
3.3. Теплопровідність.
3.3.1. Температурне поле.
Перенос
тепла теплопровідністю відбувається тільки
при наявності
різниці температур у різних
точках тіла. Процес супроводжується зміною температури,
що є функцією координат точки тіла й
часу![]()
t = (x, y, z, τ) (3.5)
Функція
визначає значення температури
для всіх точок
простору в
даний момент
часу й
описується вираженням тривимірного температурного поля. Якщо температура тіла є
функцією координат і часу (тобто
змінюється в часі
й ![]() ), то
температурне поле називається несталим
(нестаціонарним) і відповідає несталому режиму теплопровідності.
), то
температурне поле називається несталим
(нестаціонарним) і відповідає несталому режиму теплопровідності.
Якщо
температура тіла не
змінюється в часі
і є функцією тільки координат
(тобто![]() ), то таке температурне
поле називається сталим (стаціонарним) і відповідає
сталому режиму теплопровідності.
), то таке температурне
поле називається сталим (стаціонарним) і відповідає
сталому режиму теплопровідності.
Температурне поле може бути двомірним, коли t = f(х,у) (для стаціонарного поля) або t = f(x,y,τ) (для нестаціонарного поля), і одномірним – відповідно t = f(х), або t = f(х, τ).
Геометричне місце точок з однаковою температурою називається ізотермічною поверхнею.
3.3.2. Температурний градієнт.
Температура в тілі незмінна уздовж ізотермічної поверхні й зростає або убуває тільки в напрямках, непаралельних ізотермічним поверхням.
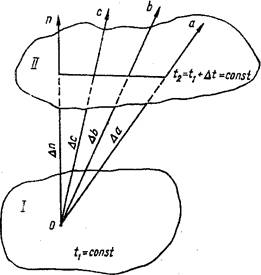 Розглянемо зміну температури
між двома ізотермічними поверхнями I й II (рис.
3.1).
Розглянемо зміну температури
між двома ізотермічними поверхнями I й II (рис.
3.1).
Рис.3.1. До визначення ізотермічних поверхонь і
температурного градієнта.
Температура в тілі буде змінюватися відносно точки О в будь - якому напрямку убік поверхні II. При цьому перепад температури на одиницю довжини буде зростати в міру наближення напрямку до нормалі, де й досягне свого максимуму.
Зміна температури в напрямку нормалі до ізотермічної поверхні характеризується температурним градієнтом:
![]() =
=![]() (3.6)
(3.6)
Температурний градієнт є вектором, спрямованим убік збільшення температури й визначає найбільшу швидкість зміни температури в даній точці.
3.3.3. Закон теплопровідності Фур'є.
Кількісну залежність теплового потоку від параметрів, що його характеризують, називають законом Фур'є, або основним законом теплопровідності.
Відповідно до закону Фур'є, кількість тепла dQ, що проходить через елементарну площадку dF за час dτ, прямо пропорційна градієнту температури ∂t/∂n, тобто
![]() (3.7)
(3.7)
![]() .
(3.7a)
.
(3.7a)
Знак мінус у цих рівняннях указує на те, що в напрямку теплового потоку температура тіла зменшується й grad t є величиною від’ємною. Коефіцієнт пропорційності λ (Вт/м К) у рівнянні (3.7) показує, яка кількість тепла проходить внаслідок теплопровідності через 1 м2 поверхні протягом 1 с на відстань 1 м при різниці температур на цій відстані в 10, і називається коефіцієнтом теплопровідності.
Значення коефіцієнта теплопровідності є фізичною характеристикою речовини й залежить від його природи, агрегатного стану й температури. При незмінності цих властивостей коефіцієнт теплопровідності речовини (матеріалу) може змінюватися залежно від особливостей його кристалічної структури, пористості, змісту домішок і вологості.
Коефіцієнт теплопровідності газів з підвищенням температури зростає й практично не залежить від тиску. Для рідин (крім води й гліцерину) і металів зі збільшенням температури λ зменшується.
Коефіцієнт теплопровідності багатьох твердих тіл зі збільшенням температури збільшується. Для більшості речовин коефіцієнти теплопровідності визначаються дослідним шляхом та наводяться в довідковій літературі.
3.3.4. Диференціальне рівняння теплопровідності.
Процес поширення тепла теплопровідністю може бути описаний математично диференціальним рівнянням.
При виводі диференціального рівняння теплопровідності прибігають до методів математичної фізики, що розглядає протікання процесів не у всій системі (тілі), а у виділеному в ній елементарному об’ємі dV за нескінченно малий відрізок часу дτ. При цьому для спрощення задачі приймаються деякі допущення: тіло ізотропне, його фізичні параметри є сталими.
Розглянемо такий елементарний об’єм з ребрами dх, dу, dz у прямокутній системі координат (рис. 3.2). Виведення диференціального рівняння теплопровідності ґрунтується на законі збереження енергії, відповідно до якого кількість введеного в об’єм тепла ззовні за відрізок часу dτ внаслідок теплопровідності дорівнює зміні внутрішньої енергії речовини.
Розкладемо загальний потік тепла, що надходить в об’єм, на складові, що паралельні осям координат. Нехай у напрямку осей через грань dуdz входить тепло Qx, через грань dхdz - Qу, через грань dхdу - Qz, а через протилежні грані виходить відповідно Qx+dx, Qу+dy, Qz+dz.
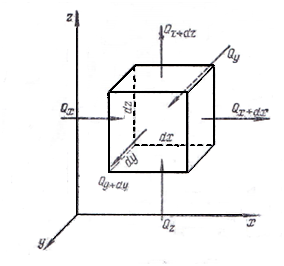 Рис. 3.2. До виводу
диференціального
Рис. 3.2. До виводу
диференціального
рівняння теплопровідності
Кількість теплоти, яка введена в паралелепіпед через всі три грані, чисельно дорівнює сумі різниць уведеного й виведеного тепла відповідними гранями, тобто
![]() .
.
У відповідність із законом Фур'є, кількість тепла, що сприймається гранню dуdz, може бути виражена як
![]() .
.
Кількість виведеного тепла в напрямку осі х
![]() .
.
Отже, кількість тепла, яка витрачена на нагрівання паралелепіпеда потоком уздовж осі х за час dτ
![]() .
.
Аналогічно для двох інших осей
![]() ,
,
![]() .
.
Загальна кількість тепла, отримана паралелепіпедом, дорівнює сумі трьох складових, тобто
![]() (3.8)
(3.8)
За законом збереження енергії кількість тепла, що введена в об’єм dV=dхdуdz, дорівнює зміні його ентальпії й може бути виражена співвідношенням
![]() ,
(3.9)
,
(3.9)
де с - теплоємність матеріалу паралелепіпеда; ρ - густина; (∂t/∂τ) - зміна температури в часі. Прирівнюючи праві частини рівнянь 3.8 й 3.9, одержимо диференціальне рівняння теплопровідності Фур'є
![]() (3.10)
(3.10)
Комплекс параметрів λ/(сρ)=a (м2/с) називається коефіцієнтом температуропровідності, він характеризує здатність матеріалу змінювати температуру в часі. Зважаючи, що
![]() ,
,
рівняння (3.10) можна записати в загальному виді
![]()
![]() . (3.10a)
. (3.10a)
Зміна кількості тепла в тілі може відбутися й за рахунок внутрішніх джерел (наприклад, хімічних реакцій). Якщо потужність такого джерела тепла для одиниці об'єму позначити qr (Вт/м3), то на весь об’єм кількість тепла внутрішніх джерел буде становити qrdV. Із урахуванням внутрішнього джерела тепла рівняння (3.10a) прийме вид
![]() .
(3.11)
.
(3.11)
3.3.5. Рівняння теплопровідності плоскої стінки.
Розглянемо передачу тепла теплопровідністю через плоску стінку (рис. 3.3а), довжина й ширина якої незрівнянно більше її товщини; вісь х розташована по нормалі до поверхні стінки.
Температури зовнішніх поверхонь стінки рівні tcт1 й tcт2, причому tcт1>tcт2.
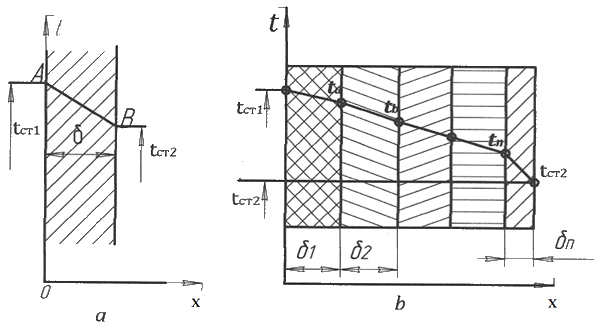 Рис. 3.3 До виводу рівняння теплопровідності плоскої
стінки:
Рис. 3.3 До виводу рівняння теплопровідності плоскої
стінки:
а-одношарова стінка; б- багатошарова стінк
При сталому процесі кількість тепла, підведеного до стінки й відведеного від неї, повинні бути рівні між собою й не повинні змінюватися в часі.
Приймемо, що температура змінюється тільки в
напрямку осі х, тобто температурне поле одномірне
![]() Тоді
на
підставі рівняння теплопровідності (3.10) маємо:
Тоді
на
підставі рівняння теплопровідності (3.10) маємо:
![]() (3.12)
(3.12)
Інтегрування цього рівняння приводить до функції
t=C1x+C2 , (3.13)
де C1 й C2 - константи інтегрування.
Рівняння (3.13) показує, що по товщині плоскої стінки температура змінюється прямолінійно. Константи інтегрування визначають виходячи з наступних граничних умов:
при х=0 величина t=tст1 , тоді з рівняння (3.13) С2= tст1.
при х=δ величина t= tст2 і рівняння (3.13) приймає вид
tст2=С1δ+С2 або tст2=С1δ+ tст1 , звідки
![]()
Підставивши значення констант С1 і С2 у рівняння (3.13), знаходимо
![]()
Тоді
![]()
Підставивши отримане вираження температурного градієнта в рівняння теплопровідності (3.7) визначимо кількість переданого тепла:
![]()
або
![]() (3.14)
(3.14)
де λ - коефіцієнт теплопровідності матеріалу стінки; δ - товщина стінки; tст1 - tст2 - різниця температур поверхонь стінки; F- поверхня стінки; τ- час.
Для безперервного процесу передачі тепла теплопровідністю при τ=1 рівняння (3.7) приймає вид
![]() (3.14a)
(3.14a)
Рівняння (3.14a) і (3.14) є рівняннями теплопровідності плоскої стінки при сталому процесі теплообміну.
Якщо плоска стінка складається з п шарів, що відрізняються один від одного теплопровідністю й товщиною (рис. 3.3б), то при сталому процесі через кожен шар стінки пройде однакова кількість тепла, яка може бути виражена для різних шарів рівняннями:
![]()
![]()
![]()
![]()
Складаючи ліві й праві частини другого стовпця цих рівнянь, одержимо
![]()
Звідки
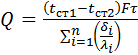 (3.15)
(3.15)
де i - порядковий номер шару стінки; п - число шарів.
Величину ![]() називають сумарним термічним опором багато-шарової стінки.
Густина теплового потоку при цьому буде дорівнювати
називають сумарним термічним опором багато-шарової стінки.
Густина теплового потоку при цьому буде дорівнювати
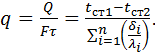 (3.15a)
(3.15a)
3.3.6. Рівняння теплопровідності циліндричної стінки. Розглянемо передачу тепла теплопровідністю через циліндричну стінку довжиною L, внутрішнім радіусом rв і зовнішнім радіусом rз (рис. 3.4а).
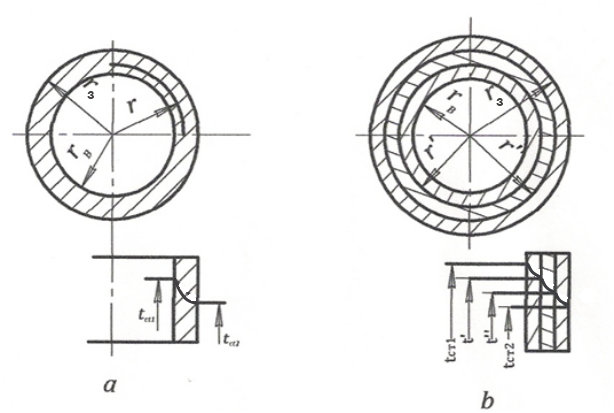 Рис. 3.4 До виводу рівняння теплопровідності
циліндричної стінки:
Рис. 3.4 До виводу рівняння теплопровідності
циліндричної стінки:
а-одношарова стінка; б- багатошарова стінка
Температури на внутрішній і зовнішній поверхнях стінки сталі і дорівнюють tcт1 й tcт2 відповідно, тобто процес теплообміну є сталим. Нехай tcт1>tcт2 і температура змінюється тільки в радіальному напрямку, тобто температурне поле одномірне. Оскільки ці поверхні не однакові, рівняння (3.14) у цьому випадку не може бути застосовано.
Для
циліндричної стінки поверхня її в деякому перерізі, що відповідає поточному
радіусу r, становить ![]() Підставивши значення F у рівняння Фур’є (3.7), знаходимо для
одномірного поля:
Підставивши значення F у рівняння Фур’є (3.7), знаходимо для
одномірного поля:
![]()
Розділивши змінні, інтегруємо це рівняння в межах від rв до rз і відповідно від tcт1 до tст2:
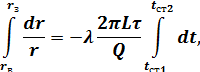
звідки
![]()
або, з огляду на те, що rз/rв = dз/dв, одержимо
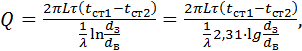 (3.16)
(3.16)
де dз/dв – відношення зовнішнього діаметра циліндричної стінки до її внутрішнього діаметра.
Рівняння (3.16) показує, що по товщині циліндричної стінки температура змінюється по криволінійному (логарифмічному) закону. Це рівняння являє собою рівняння теплопровідності циліндричної стінки при сталому процесі теплообміну.
По аналогії з виводом, наведеним для багатошарової плоскої стінки, для циліндричної стінки, що складається з п шарів, кількість тепла, що передана шляхом теплопровідності, буде становити
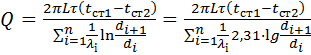 , (3.16a)
, (3.16a)
де i - порядковий номер шару стінки.
Питомий тепловий потік може бути віднесений або до одиниці довжини труби, або до одиниці внутрішньої або зовнішньої поверхні:
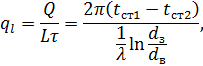
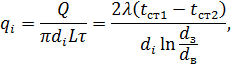
![]()
Тепловий потік, віднесений до одиниці довжини
труби (![]() називають лінійною
густиною теплового потоку або лінійним тепловим потоком.
називають лінійною
густиною теплового потоку або лінійним тепловим потоком.
Рівняння (3.15) - (3.16a) для плоскої й циліндричної стінок були отримані для стаціонарного (сталого) процесу поширення тепла теплопровідністю. Для тонких циліндричних стінок (тонкостінних труб) розрахунок може бути спрощений і виконуватися за рівнянням (3.15), як для плоскої поверхні.
3.3.7. Теплопровідність сферичної стінки. У цьому випадку для поверхні довільного радіуса r (рис. 3.5а) при одномірному температурному полі рівняння (3.7) буде мати такий вигляд:
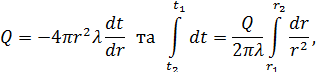
звідки одержимо (у Дж/с=Вт):
![]() (3.17)
(3.17)
З отриманого рівняння видно, що температура в сферичній стінці (у радіальному напрямку) змінюється по гіперболічній кривій.
Стосовно до окремих шарів тришарової сферичної стінки (рис. 3.5б) запишемо:
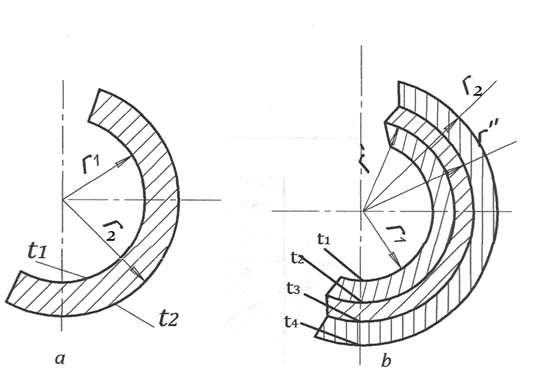
Рис 3.5 До виводу рівняння теплопровідності сферичної стінки:
a - одношарова стінка; b - багатошарова стінка
![]()
Розв’язуючи останні рівняння, як і у попередніх випадках, відносно різниць температур (t1-t2, t2-t3, t3-t4) і підсумовуючи їх, одержимо
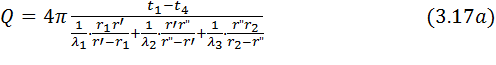
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.