
ТЕПЛОВА РАДІАЦІЯ.
1.4.1. Розрахункові формули і приклад розрахунку.
Випромінювальна здатність тіла:
![]() , (1.27)
, (1.27)
де ![]() = 0…1 – ступінь чорноти тіла;
= 0…1 – ступінь чорноти тіла;![]() = 5.67 Вт/м2К4–
коефіцієнт випромінювання абсолютно чорного тіла; Т – абсолютна температура тіла, К.
= 5.67 Вт/м2К4–
коефіцієнт випромінювання абсолютно чорного тіла; Т – абсолютна температура тіла, К.
Питома потужність теплового потоку, яка передається з поверхні одного тіла з температурою Т1 до поверхні іншого з температурою Т2 випромінюванням, для двох паралельних стінок, Вт/м2:
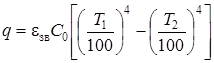 , (1.28)
, (1.28)
де зведений ступінь чорноти системи тіл:
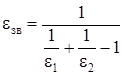 , (1.29)
, (1.29)
де ![]() ,
, ![]() –
ступені чорноти тіл.
–
ступені чорноти тіл.
Для тіл будь якої форми, з яких менше з тіл опукле:
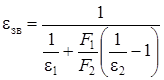 , (1.30)
, (1.30)
де F1, F2 – площі поверхонь меншого і більшого тіл відповідно, м2.
Потужність теплового потоку:
Q = q·F1 . (1.31)
Приклад. Визначити витрати теплоти випромінюванням сталевою трубкою діаметром d=70 мм, довжиною l =3 м з температурою t1 = 227ºC, якщо труба знаходиться :
а) у великому цегляному приміщенні, температура стінок якого t1 = 27ºC ;
б) у цегляному каналі, переріз якого (0,3x0,3) м2, якщо температура стінок t2 = 27ºC.
a) Згідно з умовою задачі
поверхня труби значно менша від площі поверхні стінок приміщення (F1 < < F2). Тому ![]() (див. рівняння
1.30). Для окисненої сталі (див. додаток)
(див. рівняння
1.30). Для окисненої сталі (див. додаток) ![]() =0.79. Питома потужність
згідно з (1.28):
=0.79. Питома потужність
згідно з (1.28):
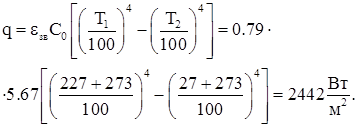
Потужність теплового потоку від поверхні труби за (1.31):
![]() ,
,
де ![]() м2.
м2.
б) Площа поверхні цегляного каналу:
![]() м2.
м2.
Згідно з додатком для цегли ступінь
чорноти ![]() .
.
Зведений ступінь чорноти:
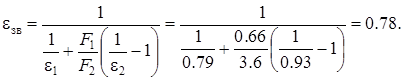
Витрати тепла з поверхні труби:
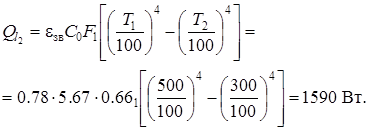
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.