
Тест по темам «Прогрессии», «Числовая последовательность», «Способы задания последовательностей»
Вариант 1
Задание 1.
В соревновании по стрельбе за каждый
промах в серии из ![]() выстрелов стрелок получал
выстрелов стрелок получал
штрафные очки: за первый промах ![]() за
каждый последующий – больше,
за
каждый последующий – больше,
 чем за предыдущий.
Сколько раз попал в цель стрелок, если он получил штрафных очков?
чем за предыдущий.
Сколько раз попал в цель стрелок, если он получил штрафных очков?
Ответ: __ раз.
Задание 2.
Запишите первые пять членов возрастающей последовательности квадратов простых чисел:
Ответ: _, _, __, __, ___.
Задание 3.
Запишите первые пять членов
возрастающей последовательности чётных натуральных чисел, не делящихся ![]()
Ответ: _, _, __, __, __.
Задание 4.
Выберите последовательности, заданные формулой, которые
являются ![]()
А) ![]()
Б) ![]()
В) 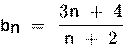
Г) 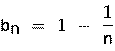
Задание 5.
Выберите верное утверждение для числовой последовательности, заданной формулой:
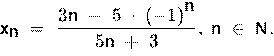
А) ограниченная
Б) неограниченная
В) ограниченная только снизу
Г) ограниченная только сверху
Задание 1. Правильный ответ: 21
Задание 2.
Правильный ответ: 4, 9, 25, 49, 121
Задание 3.
Правильный ответ: 2, 6, 10, 14, 18
Задание 4. Правильный ответ: А
Задание 5.
Правильный ответ: А
Тест по темам «Прогрессии», «Числовая последовательность», «Способы задания последовательностей»
Вариант 2
Задание 1.
В соревновании по стрельбе за каждый
промах в серии из ![]() выстрелов стрелок получал
выстрелов стрелок получал
штрафные очки: за первый промах ![]() за
каждый последующий – больше,
за
каждый последующий – больше,
 чем за
предыдущий. Сколько раз попал в цель стрелок, если он получил штрафных
очков?
чем за
предыдущий. Сколько раз попал в цель стрелок, если он получил штрафных
очков?
Ответ: __ раз.
Задание 2.
Укажите аналитическое задание последовательности всех
натуральных чисел, которые при делении ![]() дают в остатке
дают в остатке ![]()
А) ![]()
Б) ![]()
В) ![]()
Г) ![]()
Задание 3.
Выберите соответствия, задающие последовательность.
А) Каждому натуральному числу ставится в соответствие его противоположное.
Б) Каждому натуральному числу ставится в соответствие его обратное.
В) Каждому натуральному числу ставится в соответствие число 17.
Г) Каждому натуральному числу ставится в соответствие
число ![]() .
.
Задание 4.
Для каждой последовательности, заданной формулой, выберите вариант монотонности.
А) возрастающая Б) убывающая В) невозрастающая и неубывающая Варианты ответов:
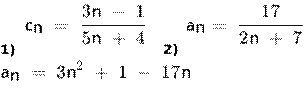 3)
3) 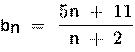 4)
4)
|
Ответ |
А |
Б |
В |
|
|
|
|
Задание 5.
Выберите верное утверждение для числовой последовательности, заданной формулой
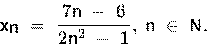
А) ограничена сверху
числом ![]()
Б) не ограничена сверху
В) ограничена снизу числом 0,005
Г) не ограничена снизу
Задание 1. Правильный ответ: 30
Задание 2. Правильный ответ: А
Задание 3.
Правильный ответ: А, Б, В Задание 4.
|
Правильный ответ: |
А |
Б |
В |
|
1 |
2, 3 |
4 |
Задание 5.
Правильный ответ: А
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.