
Вариант 1
Даны матрицы: 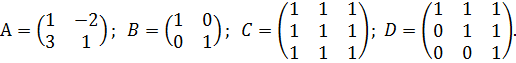
1. Среди данных матриц укажите единичную матрицу:
а) А; б) В; в) С; г) D.
2.
Вычислите ![]()
а) -7; б) -1; в) -5; г) 8.
3.
Вычислите определитель
матрицы ![]()
а) -7; б) 1; в) -5; г) 7.
4. Система линейных алгебраических уравнений называется совместной, если:
а) она имеет хотя бы одно решение; б) она имеет единственное решение;
в) все ее свободные члены равны 0; в) она не имеет решений.
5.
Для данной системы уравнений
составьте расширенную матрицу: 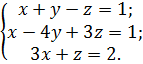
a)
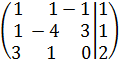 ; б)
; б) 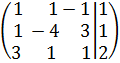 ; в)
; в) 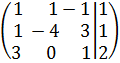 ;
;
г)
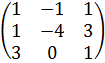 .
.
6. Даны комплексные числа z1=2+3i и z2= -4+i. Найдите z1 - z2.
а) 2+4i; б) -2+4i; в) -2+2i; г) 6+2i.
7. Найдите модуль комплексного числа z = -2 + 3i
а) ![]() ; б)
; б) ![]() ; в) 1; г
; в) 1; г![]() .
.
8.
Дано комплексное число,
записанное в тригонометрической форме ![]() . Представьте его в алгебраической форме.
. Представьте его в алгебраической форме.
а) ![]() ; б) -2+2i; в) 2+2i; г) 1+i.
; б) -2+2i; в) 2+2i; г) 1+i.
9.
Даны функции: ![]() Составьте
сложную функцию
Составьте
сложную функцию ![]()
а) ![]() б)
б)![]() в)
в)
![]() г)
г) ![]()
10. Найдите производную функции ![]()
а)![]() б)
б)![]() в)
в) ![]() г)
г)
![]()
11. Найти точки экстремума функции ![]() .
.
а) -1;1; б) 0;1; в) -1;0;1; г) -1;0.
12. Среди следующих событий укажите невозможные:
A- «Из колоды 36 карт вынули пять карт и не оказалось туза»
B- «Из колоды 36 карт вынули пять карт и все разной масти»
C- «Из колоды 36 карт вынули пять карт и все тузы»
D- «Из колоды 36 карт вынули пять карт и все пиковой масти»
а) А и В; б) А и В; в) В и С; г) В, С, D.
13. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
а) 0,8836; б) 0,12; в) 0,0036; г) 0,94.
14. В урне находится 15 шаров, из них 8 красных и 7 синих. Какова вероятность того, что среди вынутых наугад трех шаров ровно два окажутся красными? Ответ округлите до сотых.
а) 0,06; б) 0,43; в) 0,07; г) 0,20.
15. Находясь на больничном, пациент в течении 4 дней измерял температуру своего тела три раза в сутки и фиксировал результаты измерений в блокнот:
37,6; 37,8; 37,5; 37,7; 37,6; 37,2; 37,6; 37,5; 37,2; 37,5;37,2; 36,7. Какова была средняя температура больного? Ответ округлите до десятых.
а) 37,5; б) 37,6; в) 37,4; г) 37,3.
16. Вычислите предел ![]()
а) ![]() ; б) 0; в) 4; г)
1.
; б) 0; в) 4; г)
1.
17. Вычислите интеграл![]() .
.
18. Вычислите определитель матрицы 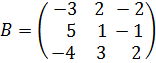 .
.
19. Решите систему уравнений методом Крамера
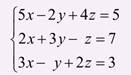
20. Найдите область определения функции ![]()
Вариант 2
Даны матрицы: 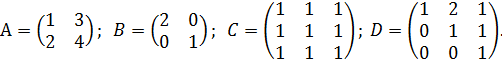
1. Среди данных матриц укажите треугольную матрицу:
а) А; б) В; в) С; г) D.
2.
Вычислите ![]()
а) -7; б) -9; в) -4; г) 8.
3.
Вычислите определитель
матрицы ![]()
а) -2; б) 10; в) 2; г) -3.
4. Система линейных алгебраических уравнений называется определенной, если:
а) она имеет хотя бы одно решение; б) она имеет единственное решение;
в) все ее свободные члены равны 0; в) она не имеет решений.
5.
Для данной системы уравнений
составьте расширенную матрицу: 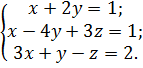
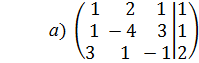 ; б)
; б)
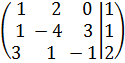 ; в)
; в)
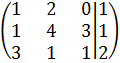 ;
;
г)
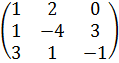 .
.
6. Даны комплексные числа z1= 2 - 3i и z2= 4 - i. Найдите z1 + z2.
а) 6 - 2i; б) 2i; в) 6 - 4i; г) 6 + 2i.
7. Найдите модуль комплексного числа z = 4- 3i
а) ![]() ; б)
; б) ![]() ; в) 1; г
; в) 1; г![]() .
.
8.
Дано комплексное число,
записанное в тригонометрической форме ![]() . Представьте его в алгебраической
форме.
. Представьте его в алгебраической
форме.
а) ![]() ; б) 2+i; в)
2+2i; г)
2.
; б) 2+i; в)
2+2i; г)
2.
9.
Даны функции: ![]() Составьте
сложную функцию
Составьте
сложную функцию ![]()
а) ![]() б)
б)![]() в)
в) ![]() г)
г)
![]()
10. Найдите производную функции ![]()
а) ![]() б)
б)![]() в)
в) ![]() г)
г)
![]()
11. Найти точки перегиба функции ![]()
а) 4;2; б) 0;1; в) -1;0;1; г) 3.
12. Среди следующих событий укажите достоверные:
A- «При подбрасывании двух игральных костей в сумме выпало четное число очков»
B- «При подбрасывании двух игральных костей в сумме выпало 7 очков»
C- «При подбрасывании двух игральных костей в сумме выпало 1 очко»
D- «При подбрасывании двух игральных костей в сумме выпало число очков меньше 13»
а) A, В, С; б) А и D; в) В и D; г) D.
13. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
а) 0,027; б) 0,27; в) 0,009; г) 0,9.
14. В урне находится 10 шаров, из них 6 красных и 4 синих. Какова вероятность того, что среди вынутых наугад четырех шаров ровно два окажутся синими? Ответ округлите до десятых.
а) 0,5; б) 0,1; в) 0,4; г) 0,6.
15. Таня вела дневник наблюдений и отмечала в нем погоду в течение двух недель в июле. Данные она занесла в таблицу: в верхней строке записаны числа, в нижней температура воздуха в градусах Цельсия.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
22 |
24 |
27 |
27 |
28 |
25 |
24 |
23 |
24 |
28 |
29 |
31 |
30 |
31 |
Определите медиану данной выборки.
а) 10; б) 23; в) 24; г) 27.
16. Вычислите предел ![]()
а) ![]() ; б) 6; в) 1; г)
0.
; б) 6; в) 1; г)
0.
17. Вычислите интеграл![]() .
.
18. Вычислите определитель матрицы 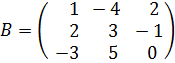 .
.
19. Решите систему уравнений методом Крамера
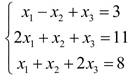
Вариант 3
Даны матрицы: 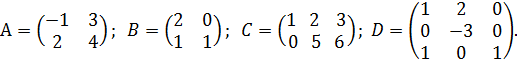
1. Среди данных матриц укажите ступенчатую матрицу:
а) А; б) В; в) С; г) D.
2.
Для матрицы D
вычислите минор ![]() :
:
а) -4; б) -1; в) 0; г) -2.
3.
Вычислите определитель
матрицы ![]()
а) 10; б) 2; в)- 10; г) 5.
4. Система линейных алгебраических уравнений называется неопределенной, если:
а) она имеет более одного решения; б) она имеет единственное решение;
в) все ее свободные члены равны 0; в) она не имеет решений.
5.
Для данной системы уравнений 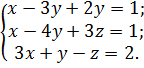 выпишите
определитель третьего порядка
выпишите
определитель третьего порядка ![]() для
нахождения переменной у по формулам Крамера:
для
нахождения переменной у по формулам Крамера:
a)
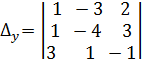 ; б)
; б)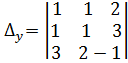 ;
;
в)
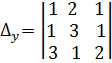 ; г)
; г)
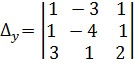 .
.
6. Даны комплексные числа z1= -5 + 4i и z2= 1 - 2i. Найдите z1 + z2.
а) -4 - 2i; б) -6 + 2i; в) 6 - 2i; г) -4 + 2i.
7. Найдите модуль комплексного числа z = -5- 3i.
а) ![]() ; б)4 в)
; б)4 в) ![]() ; г
; г![]() .
.
8.
Дано комплексное число,
записанное в тригонометрической форме ![]() . Представьте его в алгебраической
форме.
. Представьте его в алгебраической
форме.
а) ![]() б) -3; в)
-3+3i; г)
3-3i.
б) -3; в)
-3+3i; г)
3-3i.
9. Какая из следующих функций не является сложной?
а) ![]() б)
б)![]()
в) ![]() г)
г)
![]()
10. Найдите производную функции ![]()
а) ![]() б)
б)![]()
в) ![]() г)
г) ![]()
11. Найти критические точки II рода
функции ![]()
а) 0; б) -1;1; в) -1;0;1; г) 0;1.
12. В урне находится 5 красных, 4 синих и 3 зеленых шара. Из урны, не глядя, вынули четыре шара. Среди следующих событий укажите случайные:
A- «Все вынутые шары разных цветов»;
B- «Все вынутые шары красные»;
C- «В урне не осталось синих шаров»;
D- «В урне не осталось красных шаров».
а) В и С; б) В; в) A и D; г) A, В, С.
13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до тысячных.
а) 0,512; б) 0,020; в) 0,021; г) 0,05.
14. Из 4 букв разрезной азбуки составлено слово «ТРОС». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найдите вероятность того, что у него получится слово «СОРТ». Ответ округлите до тысячных.
а) 0,041; б) 0;042; в) 0,416; г) 0,04.
15. В таблице приведены данные о результатах экзамена по физике. В верхней строке указаны номера участников по списку в алфавитном порядке, а в нижней – соответствующая оценка, полученная на экзамене.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
4 |
3 |
5 |
3 |
3 |
2 |
4 |
3 |
5 |
5 |
4 |
3 |
3 |
3 |
4 |
Определите моду данной выборки.
а) 2; б) 3; в) 4; г) 5.
16. Вычислите предел ![]()
а) ![]() ; б) 6; в) 1; г)
0.
; б) 6; в) 1; г)
0.
17. Вычислите интеграл![]() .
.
18. Вычислите определитель матрицы 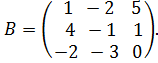
19. Решите систему уравнений методом Крамера
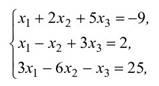
Вариант 4
Даны матрицы: 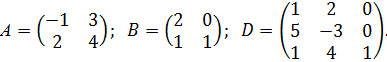
1. ![]() ранспонированная матрица
ранспонированная матрица ![]() будет
иметь вид:
будет
иметь вид:
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
2.
Вычислите матрицу ![]() :
:
а) ![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
3.
Для матрицы D
вычислите минор ![]()
а) 17; б) -23; в)- 13; г) 23.
4. Система линейных алгебраических уравнений называется однородной, если:
а) она имеет более одного решения; б) она имеет единственное решение;
в) все ее свободные члены равны 0; г) она не имеет решений.
5.
Дана расширенная матрица
системы уравнений ![]() .Тогда
сама система имеет вид:
.Тогда
сама система имеет вид:
a)
![]() б)
б)![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
6. Даны комплексные числа z1= 5 - 4i и z2= 3 - 2i. Найдите z1 - z2.
а) -2 + 2i; б) 2 - 2i; в) 2 - 6i; г) 2 + 2i.
7.
Вычислите ![]() .
.
а) ![]() ; б)
-32; в)
; б)
-32; в) ![]() ; г
; г![]() .
.
8.
Дано комплексное число,
записанное в тригонометрической форме 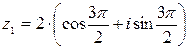 . Представьте его в алгебраической
форме.
. Представьте его в алгебраической
форме.
а) ![]() б)
-2; в)
б)
-2; в) ![]() ; г)
; г) ![]()
9. Какая из следующих функций не является сложной?
а) ![]() б)
б)![]()
в) ![]() г)
г)
![]()
10. Найдите производную функции ![]()
а) ![]() б)
б)![]()
в) ![]() г)
г)
![]()
11. Найти точки максимума функции ![]()
а) 0; б) 1; в) -1;1; г) -1.
12. В урне находится 5 красных, 4 синих и 3 зеленых шара. Из урны, не глядя, вынули четыре шара. Среди следующих событий укажите невозможные:
A- «Все вынутые шары разных цветов»;
B- «Все вынутые шары красные»;
C- «Среди вынутых не оказалось белых шаров»;
D- «В урне не осталось красных шаров».
а) А и С; б) A и D; в) С; г) A, В, С.
13. Вероятность того, что новая ручка пишет плохо (или не пишет), равна 0,04. Покупатель в магазине выбирает случайную упаковку, в которой две таких ручки. Найдите вероятность того, что обе ручки пишут хорошо.
а) 0,9216; б) 0,0016; в) 0,96; г) 0,192.
14. У Вани в кармане лежит шесть рублевых и четыре десятирублевые монеты. Он, не глядя, перекладывает три монеты в другой карман. Найдите вероятность того, что ровно две из них -рублевые.
а) 0,05; б) 0,5; в) 0,125; г) 0,2.
15. В обувном магазине продавцы ведут учет проданных размеров обуви. В один из дней распродаж были сделаны записи: 36;42;40;37;38;36;35;35;38;42;39;41;38;36;.35;38; 40.Определите размах данной выборки.
а) 42; б) 7; в) 38; г) 35.
16. Вычислите предел 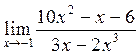
а) ![]() ; б) 0; в) 1; г)
6.
; б) 0; в) 1; г)
6.
17. Вычислите интеграл![]()
18. Вычислите определитель матрицы 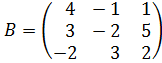 .
.
19. Решите систему уравнений
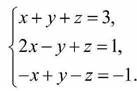
Вариант 5
Даны матрицы: 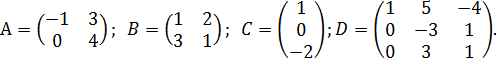
1. Среди данных матриц укажите матрицу, не являющуюся квадратной:
а) А; б) В; в) С; г) D.
2.
Вычислите ![]() .
.
а) 10; б) 31; в) -1; г) -6.
3.
Вычислите определитель
матрицы ![]()
а) 5; б) -7; в)- 4; г) -5
4. Система линейных алгебраических уравнений называется несовместной, если:
а) она имеет единственное решение; б) она не имеет решений;
в) все ее свободные члены равны 0; г) она имеет бесконечное множество решений.
5.
Дана расширенная матрица
системы уравнений ![]() .Тогда
сама система имеет вид:
.Тогда
сама система имеет вид:
a)
![]() б)
б)![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
6.
Для множеств А и В найдите ![]()
![]()
а) ![]() ; б)
; б)![]() ; в)
; в)
![]() ; г)
; г)![]()
7. В группе обучаются 24 студента. Из них 8 занимаются в секции по легкой атлетике, 12 – в футбольной секции, а 5 в обеих секциях, остальные студенты увлекаются туризмом. Сколько студентов являются туристами?
8. Среди следующих выражений выберите то, которое не является высказыванием:
а) 1 сентября- первый день осени;
б) Какой сегодня чудесный день!;
в) Январь- летний месяц;
г) 14-6=8.
9. Петя задумал число. Укажите среди следующих событий несовместные:
А- «Задуманное число - четное»
B - «Задуманное число двузначное»
C - «Задуманное число больше 10»
D - «Задуманное число оканчивается на 5»
а) А и В; б) В и С; в) A и D; г) B и D.
10. Вероятность того, что товар доставят из интернет-магазина вовремя, равна 0,8. Покупатель заказывает товар в двух интернет-магазинах. Какова вероятность того, что оба товара будут доставлены с задержкой.
а) 0,04; б) 0,4; в) 0,64; г) 0,16.
11. В коробке лежит 8 шариковых и 7 гелевых ручек. Не глядя, из коробки достают три ручки. Найдите вероятность того, что ровно две из них - шариковые. Ответ округлите до тысячных.
а) 0,062; б) 0,431; в) 0,077; г) 0,133.
12. Найдите математическое ожидание случайной величины, заданной законом распределения.
|
Х |
-4 |
-2 |
1 |
2 |
3 |
|
р |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
а) 0,6; б) 0,5; в) 0,2; г) 0,3.
13. Вика выписывала погоду в сентябре в первые 10 дней: 16;15; 18; 23; 24; 18; 16; 18; 20; 22.
Какая средняя погода была в этот период сентября?
а) 15; б) 23; в) 18; г) 19.
14. Найдите производную функции ![]()
а) ![]() б)
б)![]()
в) ![]() г)
г)
![]()
15. Найти точки перегиба функции ![]()
а) 0; б) 1; в) -1;1; г) -1.
16. Вычислите предел ![]()
а) ![]() ; б) 0; в) 1; г)
6.
; б) 0; в) 1; г)
6.
17. Вычислите интеграл![]() .
.
18. Вычислите определители матрицы 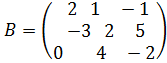 .
.
19. Решите систему уравнений методом Крамера
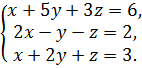
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.