
А. Г. ГЕЙН Н. А. юнОмДн
ИНФОРМАТИКА и икт
ail-
ТЕМАТИЧЕСКИЕ ТЕСТЫ
ПРОСВЕЩИ З Д А Т Е Л Ь С Т В ОЕНИЕ ЕГЭ
А. Г. ГЕЯН н. А. юнПпн
 ИНФОРМАТИКА
и ИКТ
ИНФОРМАТИКА
и ИКТ
Тематические
тесты
класс
Москва
«Просвещение»
2010
Содержание
Предисловие 4
Слово к учителю 5
Инструкция по выполнению тестовых заданий 6
|
Тест 1. Информация и формы
её |
|
|
представления (10 мин)
Тест 2. Измерение информационного |
9
|
объёма сообщения (25 мин) 15
![]()
|
Тест З. |
Формальные исполнители алгоритмов (50 мин) |
23 |
|
Тест 4. |
Алгоритмические конструкции (25 мин) |
35 |
|
Тест 5. |
Вспомогательные алгоритмы и рекурсия (60 мин) |
51 |
|
Тест 6. |
Обработка массивов (35 мин) |
63 |
|
Тест 7. |
Компьютерное моделирование (20 мин) |
83 |
|
Тест 8. |
Алгебра логики (35 мин) |
105 |
|
Тест 9. |
Базы данных (20 мин) |
117 |
|
Ключи |
к тестовым заданиям |
133 |
з
Введение тестирования становится всё более широко распространённым инструментом контроля знаний. Более того, именно тестовая процедура составляет значительную часть Единого государственного экзамена (ЕГЭ), который, с одной стороны, выступает в роли итоговой аттестации выпускников 11 класса, с другой — и это на сегодня 60лее важная составляющая — является инструментом вступительных испытаний в вузы, требующих углублённой подготовки по информатике. Основой успешного выполнения контрольных заданий, конечно, являются знания и умения, однако значительную роль играет также подготовленность к выполнению заданий в тестовой форме. С этой целью тестовые задания в данном сборнике представлены в той форме, которая близка к применяемой в ЕГЭ.
Имеется, однако, и ряд существенных отличий. Во-первых, тематика заданий несколько расширена по сравнению с классификатором ЕГЭ. Это сделано, чтобы, с одной стороны, дать более полный охват изучаемого в 11 классе материала, а с другой стороны, вовсе не исключено, что в будущем спектр тем в ЕГЭ станет шире и, в частности, будет содержать темы, пока не вошедшие в единый экзамен, но отражённые в этом сборнике. В свою очередь, задания по темам, которые уже представлены в ЕГЭ, являются некоторой модификацией тех заданий ЕГЭ, которые уже предлагались учащимся или были опубликованы в качестве демонстрационных. Тем самым предлагаемые нами задания дают достаточно полное представление об уровне и характере требований к знаниям и умениям, предъявляемых в рамках государственной аттестации выпускников основной школы.
Поскольку в 10—11 классах изучение информатики предусмотрено на базовом и профильном уровнях, в комплектах тестовых заданий по каждой теме также предусмотрено два уровня. Задания, относящиеся к профильному уровню, помечены звёздочкой (*).
Для каждой темы разработано четыре варианта тестовых заданий. Все варианты одной темы идентичны по типам заданий, уровню сложности и контролируемому в них учебному материалу.
Тестовые материалы предваряет инструкция по выполнению тестовых заданий. Она едина для всех тем. Тем не менее мы считаем полезным (по крайней мере, на первых порах) прочитывать её каждый раз перед выполнением теста.
Данный сборник может использоваться по усмотрению учителя и для организации самостоятельной (внеурочной) работы учащихся, и для проведения контрольных мероприятий на уроке. Для проверки в конце сборника приведены ключи ко всем заданиям.
Каждый тест содержит задания группы А, в которых надо выбрать один из пяти предложенных вариантов ответа, и задания группы В, в которых ответ формируется учащимся. В отличие от вариантов ЕГЭ, где обычно предлагается выбрать один из четырёх вариантов, пятый вариант заданий группы А нередко формулируется как отсутствие правильного варианта среди первых четырёк. На наш взгляд, это уменьшает соблазн для тестируемого выбрать наугад какой-нибудь из предлагаемых вариантов. Отметим, что в тестах есть задания, в которых именно пятый вариант отсутствие правильного ответа среди четырёх предыдущих является правильным.
Время выполнения тестовых заданий существенно зависит от уровня подготовленности учащихся: в сильном классе оно может быть меньше, а в более слабом классе потребуется больше времени. Короче говоря, определение времени выполнения теста остаётся за учителем. Отметим только, что для выполнения заданий группы В, как правило (но не всегда!), требуется больше времени, чем для выполнения заданий группы А. Также прерогативой учителя является начисление баллов за каждое задание.
Порядок тем в данном сборнике соответствует изложению материала в учебнике «Информатика и ИКТ» для 10 класса общеобразовательных учреждений (авторы А. Г. Гейн, А. Б. Ливчак, А. И. Сенокосов, Н. А. Юнерман). Мы считаем, однако, что предлагаемый сборник будет полезен и тем, кто работает в этой параллели по другим учебникам.
Каждый вариант теста содержит несколько заданий с выбором ответа (они отмечены буквой А в начале номера заданий) и несколько заданий, в которых ответом является последовательность символов, формируемая тестирующимся самостоятельно (эти задания отмечены буквой В).
В качестве ответа к заданиям группы А нужно указать номер того утверждения, которое вы считаете верным. Набор утверждений подобран так, что только одно из них является правильным.
В заданиях группы В ответом служит последовательность цифр или букв и цифр, разделённых между собой запятой. В ряде случаев даны образцы записи ответа. Имейте в виду, что совпадение образца с правильным ответом может оказаться случайностью. Будьте внимательны при записи ответа; к примеру, не путайте возрастание номеров и убывание.
Свои ответы записывайте в Бланк ответов, который приведён сразу после формулировок всех заданий.
Ориентировочное время, необходимое для выполнения заданий того или иного теста, вам укажет учитель. При самостоятельной работе с нашим пособием вы можете узнать наше мнение по этому вопросу, заглянув в оглавление там число, стоящее в скобках после формулировки темы, и есть время (в минутах), рекомендуемое для выполнения теста.
Задания как в части А, так и в части В не всегда располагаются в порядке возрастания сложности, и вы можете выполнять их в той последовательности, которая вам представляется наиболее удобной. В частности, можете пропустить какое-либо задание и вернуться к нему позже.
В тестовых заданиях, где используется язык программирования, текст программ приведён на языках Бейсик, Паскаль и алгоритмическом языке. В рамках одного задания все тексты программ идентичны друг другу. Естественно, что выполнять задания вы можете, используя тот язык, который вам лучше знаком. Желаем успеха!
Тест 1
Вариант 1
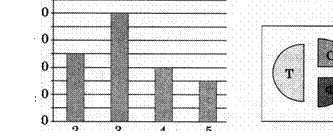
М. В цехе трудятся рабочие трёх специальностей — токари (Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший второго и не больший пятого. На первой диаграмме отражено количество рабочих, имеющих определённый разряд, а на второй — распределение рабочих по специальностям. Каждый рабочий имеет только одну специальность и один разряд.
 4 5
4 5
Имеется четыре утверждения:
А) Не могут все рабочие третьего разряда быть токарями. Б) Все рабочие третьего разряда могут быть фрезеровщиками .
В) Все слесари могут иметь пятый разряд.
Г) Кто-то из токарей имеет разряд ниже четвёртого.
Укажите, какое из этих утверждений не противоречит данным обеих диаграмм:
5) все утверждения противоречат данным на диаграммах.
В1. Ниже приведены примеры обработки информации на основании тех или иных признаков. Среди этих признаков выберите те, которые можно охарактеризовать как семантические. Номера примеров, в которых фигурируют выбранные вами признаки, запишите через запятую в порядке возрастания:
1) поиск в меню столовой овощных блюд;
2) вычёркивание из заданного списка слов всех собственных имён;
З) определение того, является ли данная часть слова приставкой;
4) выбор фильма для показа на кинофестивале;
5) определение, является ли данная денежная купюра фальшивой;
6) отбор среди десяти заданных чисел тех, которые оканчиваются цифрой З.
В2. В приведённом ниже списке указаны некоторые виды информации, воспринимаемой человеком через органы чувств. Запишите через запятую их номера в порядке возрастания доли каждого из видов информации в восприятии её человеком:
1) вкусовая; 2) визуальная;
З) обонятельная; 4) тактильная.
ВЗ. В приведённом ниже списке указано несколько процессов обработки информации. Одни из них являются формальной обработкой, а другие — эвристической. Запишите в порядке возрастания через запятую номера тех процессов, которые представляют собой формальную обработку информации:
1) вычисление площади квадрата по длине его стороны;
2) определение очередного хода в шахматной партии; З) выбор наибольшего числа в заданном наборе натуральных чисел;
4) выбор авиарейса из расписания;
5) составление
расписания уроков; ![]()
6) расположение русских слов из заданного набора в алфавитном порядке.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
вз |
|
|
|
|
|
Тест 1
Варищнт 2
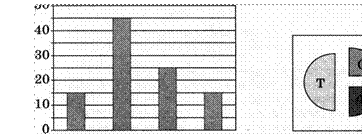
А1. В цехе трудятся рабочие трёх специальностей ![]() токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
2 з 4 5
Имеется четыре утверждения:
А) Все слесари могут иметь второй разряд.
Б) Не могут все рабочие четвёртого разряда быть фрезеровщиками.
В) Кто-то из токарей имеет разряд ниже четвёртого.
Г) Все рабочие третьего разряда могут оказаться слесарями.
Укажите, какое из этих утверждений не противоречит данным обеих диаграмм:
5) все утверждения противоречат данным на диаграммах.
В1. Ниже приведены примеры обработки информации на основании тех или иных признаков. Среди этих признаков выберите те, которые можно охарактеризовать как синтаксические. Номера примеров, в которых фигурируют выбранные вами признаки, запишите через запятую в порядке возрастания:
1) определение того, удваивать или нет букву «н» при написании данного причастия в предложении;
2) проверка в тексте наличия точки, многоточия, вопросительного или восклицательного знака в конце каждого предложения данного текста;
З) опознание преступника по фотографии;
4) определение, до сотых или до тысячных округлена данная десятичная дробь;
5) удаление из списка слов всех имён существительных;
6) розыск автомобиля на автостоянке по номеру его государственной регистрации.
В2. В приведённом ниже списке указаны некоторые виды информации, воспринимаемой человеком через органы чувств. Запишите через запятую их номера в порядке возрастания доли каждого из видов информации в восприятии её человеком:
1) визуальная; 2) обонятельная; З) звуковая; 4) тактильная.
ВЗ. В приведённом ниже списке указано несколько процессов обработки информации. Одни из них являются формальной обработкой, а другие — эвристической. Запишите в порядке возрастания через запятую номера тех процессов, которые представляют собой эвристическую обработку информации:
1) подсчёт количества делителей у заданного натурального числа;
2) выбор наиболее подходящего перевода слова с иностранного языка на русский;
З) определение победителя в закончившемся шахматном турнире;
4) вычисление площади круга по его радиусу; 5) выбор по карте маршрута для воскресного похода; 6) составление графика дежурств в классе.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
вз |
|
|
|
|
|
Тест 1
Вариант З
А1. В цехе трудятся рабочие трёх специальностей ![]() токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
40
2 з 4 5
Имеется четыре утверждения:
А) Не могут все рабочие второго разряда быть слесарями. Б) Среди рабочих третьего и четвёртого разрядов обязательно есть токари.
В) Только фрезеровщики имеют четвёртый разряд.
Г) Все рабочие третьего разряда могут оказаться фрезеровщиками.
Укажите, какое из этих утверждений не противоречит данным обеих диаграмм:
5) все утверждения противоречат данным на диаграммах.
В1. Ниже приведены примеры обработки информации на основании тех или иных признаков. Среди этих признаков выберите те, которые можно охарактеризовать как семантические. Номера примеров, в которых фигурируют выбранные вами признаки, запишите через запятую в порядке возрастания:
1) замена прописных букв, с которых начинаются слова в тексте, на заглавные;
2) определение, имеются ли в библиотеке книги данного автора;
З) определение того, какой знак — точку, многоточие, вопросительный или восклицательный знак надо поставить в конце заданного предложения;
4) поиск места в кинозале согласно купленному билету;
5) определение того, начинается ли натуральное число с той же цифры, КОТОРОЙ заканчивается;
6) определение того, являются ли два данных слова синонимами.
В2. В приведённом ниже списке указаны некоторые виды информации, воспринимаемой человеком через органы чувств. Запишите через запятую их номера в порядке возрастания доли каждого из видов информации в восприятии её человеком:
1) вкусовая; 2) визуальная;
З) звуковая; 4) обонятельная.
ВЗ. В приведённом ниже списке указано несколько процессов обработки информации. Одни из них являются формальной обработкой, а другие — эвристической. Запишите в порядке возрастания через запятую номера тех процессов, которые представляют собой формальную обработку информации:
1) вычисление значения арифметического выражения;
2) расположение фамилий участников соревнования в порядке показанных ими результатов;
З) определение очередного хода при игре в шашки;
4) выбор наибольшего числа в заданном наборе натуральных чисел;
5) выбор кинотеатра для просмотра полюбившегося фильма;
6) выбор в кафе блюда из меню.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
вз |
|
|
|
|
|
Тест 1
Вариант 4
А1. В цехе трудятся рабочие трёх специальностей ![]() токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
токари
(Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд, не меньший
второго и не больший пятого. На первой диаграмме отражено количество рабочих,
имеющих определённый разряд, а на второй — распределение рабочих по
специальностям. Каждый рабочий имеет только одну специальность и один разряд.
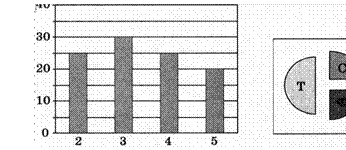
Имеется четыре утверждения:
А) Все слесари имеют пятый разряд.
Б) Не могут все рабочие четвёртого разряда быть слесарями.
В) Только токари имеют разряд не ниже четвёртого.
Г) Все рабочие третьего разряда могут оказаться фрезеровщиками.
Укажите, какое из этих утверждений не противоречит данным обеих диаграмм:
5) все утверждения противоречат данным на диаграммах.
В1. Ниже приведены примеры обработки информации на основании тех или иных признаков. Среди этих признаков выберите те, которые можно охарактеризовать как синтаксические. Номера примеров, в которых фигурируют выбранные вами признаки, запишите через запятую в порядке возрастания:
1) расположение слов в алфавитном порядке;
2) поиск афоризмов о пользе учения;
З) отбор среди десяти заданных натуральных чисел тех, которые делятся на З;
4) выбор картины, которую можно повесить на стену в классе;
5) составление списка всех произведений Л. Н. Толстого;
6) определение того, читается ли заданное слово слева направо точно так же, как справа налево.
В2. В приведённом ниже списке указаны некоторые виды информации, воспринимаемой человеком через органы чувств. Запишите через запятую их номера в порядке возрастания доли каждого из видов информации в восприятии её человеком:
1) вкусовая; 2) звуковая;
З) визуальная; 4) тактильная.
ВЗ. В приведённом ниже списке указано несколько процессов обработки информации. Одни из них являются формальной обработкой, а другие — эвристической. Запишите в порядке возрастания через запятую номера тех процессов, которые представляют собой эвристическую обработку информации:
1) вычисление длины окружности по её радиусу;
2) определение, является ли чётным заданное число;
З) определение, какая из задач в домашнем задании самая трудная;
4) выбор самого быстрого способа доехать общественным транспортом из одной точки города в другую;
5) выбор по расписанию поезда, наиболее подходящего по времени отправления;
6) выбор варианта обмена квартиры из предложенного набора вариантов.
Бланк ответов
Фамилия, имя ![]() Класс
Класс
![]()
|
|
|
|
вз |
|
|
|
|
|
Тест 2
объёма
Вариант 1
А 1. В марсианском алфавите 15 букв, в венерианском — 255 букв. Кроме того, в каждом языке есть символ «пробел», разделяющий слова. При передаче сообщений применяется двоичное кодирование, в котором каждый символ кодируется минимально возможным одинаковым числом бит.
Жители этих планет обменялись сообщениями, содержащими одинаковое количество символов. Каждый при этом писал на своём языке, поэтому информационный объём сообщений оказался разным. Укажите верное утверждение:
1) Информационный объём марсианского текста в 2 раза больше, чем венерианского.
2) Информационный объём марсианского текста в 2 раза меньше, чем венерианского.
З) Информационный объём марсианского текста в 16 раз меньше, чем венерианского.
4) Информационный объём марсианского текста в 16 раз больше, чем венерианского.
5) Нельзя определить соотношение между информационными объёмами этих сообщений, поскольку они передавались в разных алфавитах.
А2. Голубой цвет на графическом экране кодируется как 0011. Объём видеокарты 125 Кб. Определите максимально возможную разрешающую способность экрана:
1) 640х200 2) 320х400 3) 640х400
4) 640х800 5) 512х400
АЗ. В процессе преобразования растрового графического файла его объём уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 256-цветной палитре?
1) 3072 2) 384 2048
5) 4096
200
375
их
![]()
Все символы алфавита кодируются одним и тем же минимально необходимым числом бит. Сколько бит информации в этом сообщении?
ВЗ. В некоторой системе связи скорость передачи составляет 256 ООО бит в секунду. На передачу файла с несжатой монофонической музыкой потребовалась 1 минута 50 секунд. Укажите количество уровней квантования при оцифровке этой музыки, если известно, что её продолжительность составила 1 минуту 4 секунды и оцифровка производилась с частотой дискретизации 44 ООО Гц.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 2
объёма
Вариант 2
А1. В марсианском алфавите 15 букв, в венерианском — 63 буквы. Кроме того, в каждом языке есть символ «пробел», разделяющий слова. При передаче сообщений применяется двоичное кодирование, в котором каждый символ кодируется минимально возможным одинаковым числом бит.
Жители этих планет обменялись сообщениями, но марсианское послание содержало в З раза больше символов. Каждый при этом писал на своём языке, поэтому соотношение между информационными объёмами сообщений оказалось иным. Укажите верное утверждение:
1) Информационный объём марсианского текста в З раза больше, чем венерианского.
2) Информационный объём марсианского текста в 2 раза больше, чем венерианского.
З) Информационный объём марсианского текста такой же, как и венерианского.
4) Информационный объём марсианского текста в 2 раза меньше, чем венерианского.
5) Нельзя определить соотношение между информационными объёмами этих сообщений, поскольку они передавались в разных алфавитах.
А2. Красный цвет на графическом экране кодируется как 0101, Объём видеокарты — 250 Кб. Определите максимально возможную разрешающую способность экрана:
1) 1024х800 2) 1024х400 3) 640х400 4) 640х800 5) 500х400
АЗ. В процессе преобразования растрового графического файла его объём уменьшился в 2 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 64-цветной палитре?
2)
4096 128 ![]() 32
32
2—Гейн. Тесты. 10 кл.
100
375
их
eocvxJezoevxo,v
Все символы алфавита кодируются одним и тем же минимально необходимым числом бит. Сколько бит информации в этом сообщении?
ВЗ. В системе связи скорость передачи составляет 128 ООО бит в секунду. На передачу файла с несжатой монофонической музыкой потребовалось 2 минуты 45 секунд. Укажите количество уровней квантования при оцифровке этой музыки, если известно, что её продолжительность составила 1 минуту и оцифровка производилась с частотой дискретизации 22 ООО Гц.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
АЗ |
|
|
вз |
|
|
|
|
|
|
|
Тест 2
объёма
Вариант З
А 1. В марсианском алфавите 7 букв, в венерианском — на 120 букв больше. Кроме того, в каждом языке есть символ «пробел», разделяющий слова. При передаче сообщений применяется двоичное кодирование, в котором каждый символ кодируется минимально возможным одинаковым числом бит.
Жители этих планет обменялись сообщениями, содержащими одинаковое количество символов. Каждый при этом писал на своём языке, поэтому информационный объём сообщений оказался разным. Укажите верное утверждение:
1) Информационный объём марсианского текста в 16 раз меньше, чем объём венерианского.
2) Информационный объём марсианского текста такой же, как и венерианского.
З) Информационный объём марсианского текста в З раза меньше, чем венерианского.
4) Нельзя определить соотношение между информационными объёмами этих сообщений, поскольку они передавались в разных алфавитах.
5) Ни одно из утверждений не является верным.
А2. Синий цвет на графическом экране кодируется как 0111. Объём видеокарты — 0,5 Мб. Определите максимально возможную разрешающую способность экрана:
1) 1200х800 2) 1024х512 3) 1600х800
![]()
АЗ. В процессе преобразования растрового изображения с тем же разрешением, но использованием 1024-цветной палитры объём графического файла увеличился в 2 раза. Сколько цветов было в палитре первоначального изображения?
1) 2048 2) 512 32
5) 20
ЗОО
750
их
![]() ос б П
ос б П
Все символы алфавита кодируются одним и тем же минимально необходимым числом бит. Сколько бит информации в этом сообщении?
ВЗ. В системе связи скорость передачи составляет 256 ООО бит в секунду. На передачу файла с несжатой монофонической музыкой потребовалось 2 минуты 45 секунд. Укажите количество уровней квантования при оцифровке этой музыки, если известно, что её продолжительность составила 1 минуту 20 секунд и оцифровка производилась с частотой дискретизации 44 ООО Гц.
![]() Бланк ответов
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 2
объёма
Вариант 4
А1. В марсианском алфавите 15 букв, а в венерианском — на 240 букв больше. Кроме того, в каждом языке есть символ «пробел», разделяющий слова. При передаче сообщений применяется двоичное кодирование, в котором каждый символ кодируется минимально возможным одинаковым числом бит.
Жители этих планет обменялись сообщениями, но марсианское послание по количеству символов оказалось в 2 раза длиннее. Каждый при этом писал на своём языке, поэтому соотношение между информационными объёмами сообщений оказалось иным. Укажите верное утверждение:
1) Информационный объём марсианского текста в 2 раза больше, чем венерианского.
2) Информационный объём марсианского текста такой же, как и венерианского.
З) Информационный объём марсианского текста в 8,5 раза меньше, чем венерианского.
4) Нельзя определить соотношение между информационными объёмами этих сообщений, поскольку они передавались в разных алфавитах.
5) Ни одно из утверждений не является верным.
А2. Зелёный цвет на графическом экране кодируется как 1001. Объём видеокарты — 500 Кб. Определите максимально возможную разрешающую способность экрана:
1) 1200х900 2) 1024х512 3) 1600х800 4) 1600х500 5) 1024х900
АЗ. В процессе преобразования растрового изображения с тем же разрешением, но с использованием 512-цветной палитры объём графического файла увеличился в 3 раза. Сколько цветов было в палитре первоначального изображения?
2) 1536
250 З
750 Сколько символов в алфавите?
В2. Сообщение, присланное от инопланетян, оказалось записанным с помощью всех символов их алфавита. Вот это сообщение:
![]()
Все символы алфавита кодируются одним и тем же минимально необходимым числом бит. Сколько бит информации в этом сообщении?
ВЗ. В системе связи скорость передачи составляет 256 ООО бит в секунду. На передачу файла с несжатой монофонической музыкой потребовалось 4 минуты 35 секунд. Укажите количество уровней квантования при оцифровке этой музыки, если известно, что её продолжительнбсть составила 1 минуту 20 секунд и оцифровка производилась с частотой дискретизации 22 ООО Гц.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
АЗ |
|
|
вз |
|
|
|
|
|
|
|
Тест З
Формальные исполнители алгоритмов
Вариант 1
А 1. Имеется полоска клетчатой бумаги шириной в 1 клетку и длиной в 6 клеток. Робот может закрасить клетку, на которой он находится, в красный, жёлтый или зелёный цвет (неважно, каким цветом была закрашена клетка до этого), а также переместиться на 1 клетку вправо или влево. Робот умеет также проверять, какого цвета клетка, на которой он находится. Если робот стоит у края полоски и получает команду переместиться за край, то он выходит из строя. Первоначально клетки полоски (по порядку слева направо) выкрашены так: красная, жёлтая, жёлтая, красная, зелёная, красная. Робот стоит на самой левой клетке и исполняет следующий алгоритм:
Алгоритм
{ Если (находится на зелёной клетке) r.Q
{ Закрасить клетку в красный цвет;
Дедах» пока (находится не на зелёной клетке)
{ Перейти вправо;
Делать пока (находится на зелёной клетке) { Закрасить клетку в жёлтый цвет; Перейти влево;
Еели (находится на жёлтой клетке) r.Q
{ Закрасить клетку в красный цвет; Перейти вправо;
Если (находится на красной клетке) ![]()
{ Закрасить клетку в зелёный цвет;
Перейти влево;
Перейти влево;
Перейти влево;
Через некоторое время Робот прекратил работу. В этот момент:
1) он стоит на жёлтой клетке;
2) он стоит на красной клетке; З) он стоит на зелёной клетке;
4) он вышел из строя при попытке перейти правый край полоски;
5) он вышел из строя при попытке перейти левый край полоски.
А2. Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены перегородки, сквозь которые Робот пройти не может. Робот также для каждой стороны той клетки, где он находится, умеет проверять истинность условия отсутствия стены. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение программы прервётся.
Робот, находясь на поле, изображённом на рисунке, исполняет следующий алгоритм:
 Алгоритм
Алгоритм
{ Делать дока (це сверху стена)
{ Вверх;
Вправо;
Дедах» пока (не слева стена)
{ Влево;
Вверх;
При успешном исполнении алгоритма длиной пути робота считается количество переходов из клетки в соседнюю клетку. Робот начинает исполнение алгоритма в одной из перечисленных ниже клеток. Укажите, для какой из этих клеток путь Робота окажется самым длинным.
3) сз
АЗ. Автомат может находиться в одном из четырёх состояний: 81, 82, s3 и s4. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.

Укажите, какая из перечисленных ниже программ переводит автомат в одно и то же состояние независимо от того, в каком состоянии он находился перед исполнением программы.
1) baaab 2) bababa 3) аЬЬаЬ 4) ababbaa
5) ни одна из данных программ не приводит к указанной цели
В1. Исполнитель Квадр2 имеет два допустимых действия:
а) возвести число, записанное на табло исполнителя, в квадрат;
б) вычесть 2 из числа, записанного на табло исполнителя.
После исполнения каждого действия на табло записывается результат.
Команду на исполнение первого действия будем обозначать через К, второго — через В. Последовательность КВ означает, что сначала число возводится в квадрат, а из результата вычитается 2; запись ВК означает, что сначала из числа вычитается 2, а затем результат возводится в квадрат. Требуется составить последовательность команд, предписывающую исполнителю из числа 5 получить число 35 и содержащую не более 12 команд. Если таких последовательностей несколько, то запишите любую из них; если это невозможно, запишите в ответ число О.
В2. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут находиться стены. Робот может выполнять команды 1 (вверх), 2 (вниз), З (влево), 4 (вправо), переходя на соседнюю клетку в направлении, указанном в скобках. При попытке пройти сквозь стену Робот разрушается. Робот успешно выполнил программу
3314214
и остановился в некоторой клетке.
Запишите последовательность из З команд, которую должен выполнить Робот, чтобы, начав с той клетки, где он остановился, вернуться на ту клетку, где Робот был до выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле. Если таких последовательностей несколько, то в ответ запишите их через запятую.
ВЗ. При обработке строки символов ABCDEF был применён следующий алгоритм: если первая буква строки гласная, то перемещаем её на вторую с конца позицию, а если согласная, то перемещаем её в конец строки. Требуется, применив несколько раз этот алгоритм, получить последовательность FBCEAD. Какое наименьшее число раз нужно применить этот алгоритм? Если указанную строку символов получить невозможно, то в качестве ответа запишите число —1.
В4*. Автомат может находиться в одном из пяти состояний: s1, s2, 83, s4 и 85. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.

Для сокращения записи повторяющиеся фрагменты
последовательности букв будем записывать используя показатель степени.
Например, запись (aba) это сокращённая запись программы abaabaaba, а программу
aaababab можно записать как ![]() или как
или как![]()
Рассматриваются программы вида ![]() где п
где п ![]() натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния в
состояние s4?
натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния в
состояние s4?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест З
Формальные исполнители алгоритмов
Вариант 2
А1. Имеется полоска клетчатой бумаги шириной в 1 клетку и длиной в 6 клеток. Робот может закрасить клетку, на которой он находится, в красный, жёлтый или зелёный цвет (неважно, каким цветом была закрашена клетка до этого), а также переместиться на 1 клетку вправо или влево. Робот умеет также проверять, какого цвета клетка, на которой он находится. Если Робот стоит у края полоски и получает команду переместиться за край, то он выходит из строя. Первоначально клетки полоски (по порядку слева направо) выкрашены так: красная, жёлтая, зелёная, красная, зелёная, красная. Робот стоит на самой левой клетке и исполняет следующий алгоритм:
Алгоритм
{ Если
(находится на зелёной клетке) то![]()
{ Закрасить клетку в красный цвет;
Делать пока (находится не на зелёной клетке)
{ Перейти вправо;
Делать (находится на зелёной клетке) { Закрасить клетку в жёлтый цвет; Перейти влево;
Если (находится на жёлтой клетке) то
{ Закрасить клетку в красный цвет; Перейти вправо;
Если (находится на красной клетке) то
{ Закрасить клетку в зелёный цвет;
Перейти влево;
Перейти влево; Перейти влево;
Через некоторое время Робот прекратил работу. в этот момент:
1) он стоит на жёлтой клетке;
2) он стоит на красной клетке; З) он стоит на зелёной клетке;
4) он вышел из строя при попытке перейти правый край полоски;
5) он вышел из строя при попытке перейти левый край полоски.
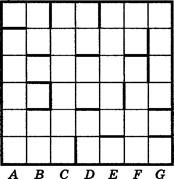
А2. Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены перегородки, сквозь которые Робот пройти не может. Робот также для каждой стороны той клетки, где он находится, умеет проверять истинность условия отсутствия стены. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение программы прервётся.
Робот, находясь на поле, изображённом на рисунке, исполняет следующий алгоритм:
 Алгоритм
6
Алгоритм
6
{ Делать пока (не справа стена)
5Вправо;
Вверх; 4
Делать пока (це снизу стена) З
{ Вниз;
Вправо; 2
1
При успешном исполнении алгоритма длиной пути
Робота считается количество переходов из клетки в соседнюю клетку. Робот начинает исполнение алгоритма в одной из перечисленных ниже клеток. Укажите, для какой из этих клеток путь Робота окажется самым длинным.
АЗ. Автомат может находиться в одном из четырёх состояний: 81 , Ч, s3 и s4. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.

Укажите, какая из перечисленных ниже программ переводит автомат в одно и то же состояние независимо от того, в каком состоянии он находился перед исполнением программы.
1) ababa 2) baabaa З) baabb 4) babaab
5) ни одна из данных программ не приводит к указанной цели.
В1. Исполнитель КвадрЗ имеет два допустимых дей-
СТВИЯ.•
а) возвести число, записанное на табло исполнителя, в квадрат;
б) вычесть З из числа, записанного на табло исполнителя.
После исполнения каждого действия на табло записывается результат.
Команду на исполнение первого действия будем обозначать через К, второго — через В. Последовательность КВ означает, что сначала число возводится в квадрат, а из результата вычитается З; запись ВК означает, что сначала из числа вычитается З, а затем результат возводится в квадрат. Требуется составить последовательность команд, предписывающую исполнителю из числа 5 получить число 31 и содержащую не более 11 команд. Если таких последовательностей несколько, то запишите любую из них; если это невозможно, запишите в ответ число О.
В2. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут находиться стены. Робот может выполнять команды 1 (вверх), 2 (вниз), З (влево), 4 (вправо), переходя на соседнюю клетку в направлении, указанном в скобках. При попытке пройти сквозь стену Робот разрушается. Робот успешно выполнил программу
4423123
и остановился в некоторой клетке.
Запишите последовательность из З команд, которую должен выполнить Робот, чтобы, начав с той клетки, где
он остановился, вернуться на ту клетку, где Робот был до выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле. Если таких последовательностей несколько, то в ответ запишите их через запятую.
ВЗ. При обработке строки символов ABCDEF был применён следующий алгоритм: если первая буква строки гласная, то перемещаем её в конец строки, а если согласная, то меняем её местами с последней буквой строки. Требуется, применив несколько раз этот алгоритм, получить последовательность EBCDAF. Какое наименьшее число раз нужно применить этот алгоритм? Если указанную строку символов получить невозможно, то в качестве ответа запишите число —1.
В4*. Автомат может находиться в одном из пяти состояний: Ч, s2, s3, и «95. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.
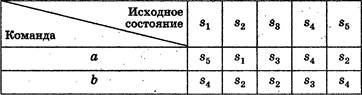
Для сокращения записи повторяющиеся фрагменты
последовательности букв будем записывать используя показатель степени.
Например, запись (aba) это сокращённая запись программы abaabaaba, а программу
aaababab можно записать как ![]() или как
или как![]()
Рассматриваются программы вида ![]() где п
где п ![]() натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния в
состояние 83?
натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния в
состояние 83?
Бланк ответов
Фамилия, имя ![]() Класс
Класс
![]()
|
М |
А2 |
АЗ |
|
ва |
вз |
|
|
|
|
|
|
|
|
|
зо
Тест З
Формальные исполнители алгоритмов
Вариант З
А 1. Имеется полоска клетчатой бумаги шириной в 1 клетку и длиной в 6 клеток. Робот может закрасить клетку, на которой он находится, в красный, жёлтый или зелёный цвет (неважно, каким цветом была закрашена клетка до этого), а также переместиться на 1 клетку вправо или влево. Робот умеет также проверять, какого цвета клетка, на которой он находится. Если Робот стоит у края полоски и получает команду переместиться за край, то он выходит из строя. Первоначально клетки полоски (по порядку слева направо) выкрашены так: красная, жёлтая, красная, зелёная, жёлтая, красная. Робот стоит на самой левой клетке и исполняет следующий алгоритм:
Алгоритм
{ Если
(находится на зелёной клетке) то![]()
{ Закрасить клетку в красный цвет;
Дедах» пока (находится не на зелёной клетке)
{ Перейти вправо;
Делать пока (находится на зелёной клетке)
{ Закрасить клетку в жёлтый цвет; Перейти влево;
Если (находится на жёлтой клетке) то![]()
{ Закрасить клетку в красный цвет;
Перейти вправо; ![]()
Если (находится на красной клетке) ![]() { Закрасить клетку в зелёный цвет;
{ Закрасить клетку в зелёный цвет;
Перейти влево;
Перейти влево;
Перейти влево;
Через некоторое время Робот прекратил работу. В этот момент:
1) он стоит на жёлтой клетке;
2) он стоит на красной клетке; З) он стоит на зелёной клетке;
4) он вышел из строя при попытке перейти правый край полоски;
5) он вышел из строя при попытке перейти левый край полоски.
А2. Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены перегородки, сквозь которые Робот пройти не может. Робот также для каждой стороны той клетки, где он находится, умеет проверять истинность условия отсутствия стены. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение программы прервётся.
Робот, находясь на поле, изображённом на рисунке, исполняет следующий алгоритм:
 Алгоритм
Алгоритм
{ Делать пока (не снизу стена)
{ Вниз;
Вправо;
Делать пока (не сверху стена)
{ Вверх;
Вправо;
При успешном исполне-
А В С D Е F G нии алгоритма длиной пути
Робота считается количество переходов из клетки в соседнюю клетку. Робот начинает исполнение алгоритма в одной из перечисленных ниже клеток. Укажите, для какой из этих клеток путь Робота окажется самым длинным.
2) АЗ 3) сз
АЗ. Автомат может находиться в одном из четырёх состояний: 81 , s2, и 84. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.

Укажите, какая из перечисленных ниже программ переводит автомат в одно и то же состояние независимо от того, в каком состоянии он находился перед исполнением программы.
1) ababa 2) bababa З) bbbaa 4) aabaab
5) ни одна из данных программ не приводит к указанной цели
В1. Исполнитель Квадр4 имеет два допустимых действия:
а) возвести число, записанное на табло исполнителя, в квадрат;
б) вычесть 4 из числа, записанного на табло исполнителя.
После исполнения каждого действия на табло записывается результат.
Команду на исполнение первого действия будем обозначать через К, второго — через В. Последовательность КВ означает, что сначала число возводится в квадрат, а из результата вычитается 4; запись ВК означает, что сначала из числа вычитается 4, а затем результат возводится в квадрат. Требуется составить последовательность команд, предписывающую исполнителю из числа 7 получить число 17 и содержащую не более 7 команд. Если таких последовательностей несколько, то запишите любую из них; если это невозможно, запишите в ответ число О.
В2. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут находиться стены. Робот может выполнять команды 1 (вверх), 2 (вниз), З (влево), 4 (вправо), переходя на соседнюю клетку в направлении, указанном в скобках. При попытке пройти сквозь стену Робот разрушается. Робот успешно выполнил программу
1132432
и остановился в некоторой клетке.
Запишите последовательность из З команд, которую должен выполнить Робот, чтобы, начав с той клетки, где
З—Гейн. Тесты. 10 кл.
он остановился, вернуться на ту клетку, где Робот был до выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле. Если таких последовательностей несколько, то в ответ запишите их через запятую.
ВЗ. При обработке строки символов ABCDEF был применён следующий алгоритм: если первая буква строки гласная, то перемещаем её в конец строки, а если согласная, то меняем её местами с последней буквой строки. Требуется, применив несколько раз этот алгоритм, получить последовательность FBDCAE. Какое наименьшее число раз нужно применить этот алгоритм? Если указанную строку символов получить невозможно, то в качестве ответа запишите число —1.
В4*. Автомат может находиться в одном из пяти состояний: s1, 82, 83, и s5. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя • записывается как соответствующая последовательность букв а и Ь. В таблице указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.
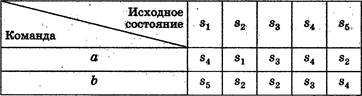
Для сокращения записи повторяющиеся фрагменты последовательности букв будем записывать используя показатель степени. Например, запись (aba) это сокращённая запись программы abaabaaba, а прогеамму aaababab можно записать как или как а (ab) .
Рассматриваются программы вида где п ![]() натуральное число,
меньшее 10. Сколько таких программ переводят автомат из состояния в состояние
83?
натуральное число,
меньшее 10. Сколько таких программ переводят автомат из состояния в состояние
83?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
|
|
вз |
|
|
|
|
|
|
|
|
|
Тест З
Формальные исполнители алгоритмов
Вариант 4
А 1. Имеется полоска клетчатой бумаги шириной в 1 клетку и длиной в 6 клеток. Робот может закрасить клетку, на которой он находится, в красный, жёлтый или зелёный цвет (неважно, каким цветом была закрашена клетка до этого), а также переместиться на 1 клетку вправо или влево. Робот умеет также проверять, какого цвета клетка, на которой он находится. Если Робот стоит у края полоски и получает команду переместиться за край, то он выходит из строя. Первоначально клетки полоски (по порядку слева направо) выкрашены так: красная, жёлтая, красная, зелёная, жёлтая, красная. Робот стоит на самой левой клетке и исполняет следующий алгоритм:
Алго итм
{ Если
(находится на зелёной клетке) то![]()
{ Закрасить клетку в красный цвет;
Делать пока (находится не на зелёной клетке)
{ Перейти вправо;
Делать пока (находится на зелёной клетке)
{ Закрасить клетку в жёлтый цвет; Перейти влево;
Если (находится на жёлтой клетке) то
{ Закрасить клетку в красный цвет; Перейти вправо;
Если (находится на красной клетке) то
{ Закрасить клетку в зелёный цвет;
Перейти влево;
Перейти влево;
Перейти влево;
Через некоторое время Робот прекратил работу. В этот момент:
1) он стоит на жёлтой клетке;
2) он стоит на красной клетке; З) он стоит на зелёной клетке;
4) он вышел из строя при попытке перейти правый край полоски;
5) он вышел из строя при попытке перейти левый край полоски.
А2. Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены перегородки, сквозь которые Робот пройти не может. Робот также для каждой стороны той клетки, где он находится, умеет проверять истинность условия отсутствия стены. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение программы прервётся.
Робот, находясь на поле, изображённом на рисунке, исполняет следующий алгоритм:
Алгоритм
 6{ Делать
пока (не справа стена)
6{ Делать
пока (не справа стена)
{ Вправо; 5
Вниз;
4 деда» пока (не сверху стена) з{ Вверх;
Вправо; 2
1
При успешном исполне-
А В С D Е F G нии алгоритма длиной пути
Робота считается количество переходов из клетки в соседнюю клетку. Робот начинает исполнение алгоритма в одной из перечисленных ниже клеток. Укажите, для какой из этих клеток путь Робота окажется самым длинным.
![]() АЗ. Автомат может находиться в одном из
четырёх состояний: 81, s2, s3 и 84. Кроме того, автомат понимает две команды,
одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого
исполнителя записывается как соответствующая последовательность букв а и Ь. В
таблице указано, как меняется исходное состояние автомата после исполнения им
соответствующей команды.
АЗ. Автомат может находиться в одном из
четырёх состояний: 81, s2, s3 и 84. Кроме того, автомат понимает две команды,
одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого
исполнителя записывается как соответствующая последовательность букв а и Ь. В
таблице указано, как меняется исходное состояние автомата после исполнения им
соответствующей команды.

Укажите, какая из перечисленных ниже программ переводит автомат в одно и то же состояние независимо от того, в каком состоянии он находился перед исполнением программы.
1) ababa 2) ababba 3) ЬаЬаЬ 4) bababb
5) ни одна из данных программ не приводит к указанной цели
В1. Исполнитель Квадр5 имеет два допустимых действия:
а) возвести число, записанное на табло исполнителя, в квадрат;
б) вычесть 5 из числа, записанного на табло исполнителя.
После исполнения каждого действия на табло записывается результат.
Команду на исполнение первого действия будем обозначать через К, второго через В. Последовательность КВ означает, что сначала число возводится в квадрат, а из результата вычитается 5; запись ВК означает, что сначала из числа вычитается 5, а затем результат возводится в квадрат. Требуется составить последовательность команд, предписывающую исполнителю из числа 7 получить число 17 и содержащую не более 20 команд. Если таких последовательностей несколько, то запишите любую из них; если это невозможно, запишите в ответ число О.
В2. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут находиться стены. Робот может выполнять команды 1 (вверх), 2 (вниз), З (влево), 4 (вправо), переходя на соседнюю клетку в направлении, указанном в скобках. При попытке пройти сквозь стену Робот разрушается. Робот успешно выполнил программу
2241341
и остановился в некоторой клетке.
Запишите последовательность из З команд, которую должен выполнить Робот, чтобы, начав с той клетки, где он остановился, вернуться на ту клетку, где Робот был до выполнения программы, и не разрушиться, вне зависимости от того, какие стены стоят на поле. Если таких последовательностей несколько, то в ответ запишите их через запятую.
ВЗ. При обработке строки символов ABCDEF был применён следующий алгоритм: если первая буква строки согласная, то перемещаем её на вторую с конца позицию, а если гласная, то перемещаем её в конец строки. Требуется, применив несколько раз этот алгоритм, получить последовательность CDAFBE. Какое наименьшее число раз нужно применить этот алгоритм? Если указанную строку символов получить невозможно, то в качестве ответа запишите число —1.
В4*. Автомат может находиться в одном из пяти состояний: «91 , Ч, Ч, и s5. Кроме того, автомат понимает две команды, одна из которых обозначена буквой а, другая — буквой Ь. Программа для этого исполнителя записывается как соответствующая последовательность букв а и Ь. В строках таблицы указано, как меняется исходное состояние автомата после исполнения им соответствующей команды.
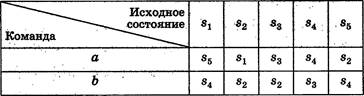
Для сокращения записи повторяющиеся фрагменты
последовательности букв будем записывать используя показатель степени.
Например, запись (aba) это сокращённая запись программы abaabaaba, а программу
aaababab можно записать как ![]() или как
или как![]()
Рассматриваются программы вида (ЬаЬ)Па, где п ![]() натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния s1
снова в состояние 81?
натуральное
число, меньшее 10. Сколько таких программ переводят автомат из состояния s1
снова в состояние 81?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
|
|
вз |
|
|
|
|
|
|
|
|
|
Тест 4
Алгоритмические конструкции
Вариант 1
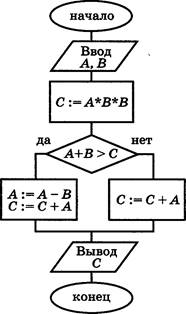
А1. На рисунке изображён фрагмент схемы алгоритма.
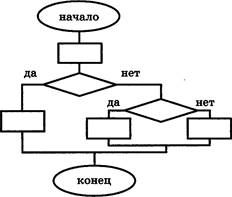
Укажите верное высказывание об этом фрагменте:
1) схема содержит команду ветвления в сокращённой форме, в которую вложена команда ветвления в полной форме;
2) схема содержит две команды ветвления в полной форме, одна из которых вложена в другую;
З) схема содержит две команды ветвления в сокращённой форме, одна из которых вложена в другую;
4) схема содержит команду ветвления в полной форме, в которую вложена команда ветвления в сокращённой форме;
5) ни одно из высказываний не является верным.
А2. Дан алгоритм, схема которого изображена на рисунке. При каких наборах начальных значений х, у и z, перечисленных ниже, тело цикла будет исполняться ровно З раза?
![]()
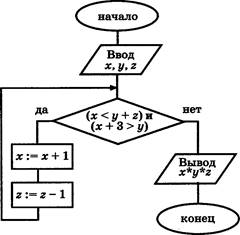
В1. На рисунке изображён алгоритм. Определите, сколько раз в этом фрагменте будет исполняться тело цикла.
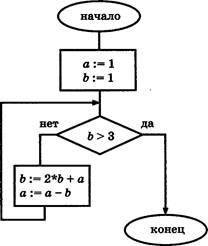
В2. Найдите значение переменной а после исполнения
алгоритма, схема которого изображена на рисунке.![]()
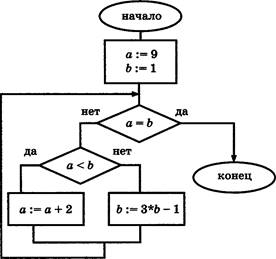
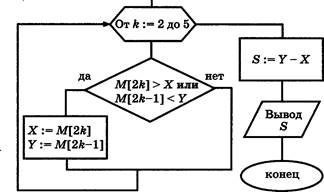
ВЗ. Дан алгоритм, схема которого изображена на рисунке.
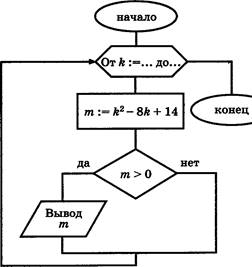
В заголовке цикла «От : . до ... » стёрты границы изменения переменной К. Однако имеются результаты работы этого алгоритма — было напечатано три числа: 7; 2; 2. В бланке ответов запишите через запятую границы изменения К.
В4. Дан алгоритм, схема которого изображена на рисунке.
Алгоритм был исполнен для трёх наборов значений переменных А
и В: А = 1, В![]()
А = —1, В = 1. Чему равна сумма полученных значений переменной С?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
|
вз |
|
|
|
|
|
|
|
|
42
|
Тест 4 |
|
|
Алгоритмические конструкции
Вариант 2
А1. На рисунке изображён фрагмент схемы алгоритма.
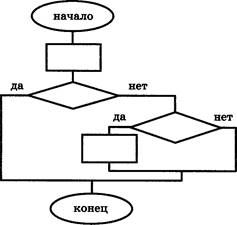
Укажите верное высказывание об этом фрагменте: 1) схема содержит команду ветвления в сокращённой форме, в которую вложена команда ветвления в полной форме;
2) схема содержит две команды ветвления в полной форме, одна из которых вложена в другую;
З) схема содержит две команды ветвления в сокращённой форме, одна из которых вложена в другую;
4) схема содержит команду ветвления в полной форме, в которую вложена команда ветвления в сокращённой форме;
5) ни одно из высказываний не является верным.
А2. Дан алгоритм, схема которого изображена на рисунке. При каких наборах начальных значений х, у и г, перечисленных ниже, тело цикла будет исполняться ровно З раза?
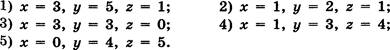
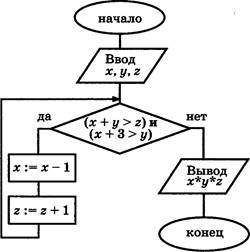
В1. На рисунке изображён алгоритм.
Определите, сколько раз в этом фрагменте будет ис полняться тело цикла.
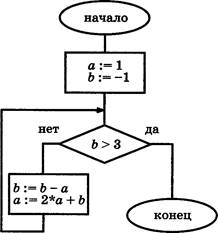
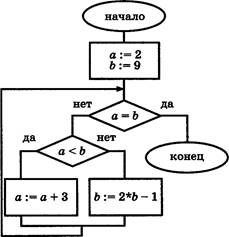
В2. Найдите значение переменной а после исполнения алгоритма, схема КОТОРОГО изображена на рисунке.
ВЗ. Дан алгоритм, схема которого изображена на рисунке.
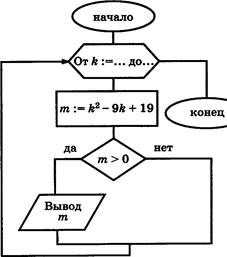
В заголовке цикла «От К . до ... » стёрты границы изменения переменной К. Однако имеются результаты работы этого алгоритма было напечатано три числа: 1; 1; 5. В бланке ответов запишите через запятую границы изменения К.
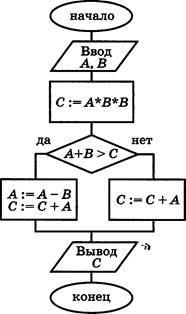
В4. Дан алгоритм, схема которого изображена на рисунке.
Алгоритм был исполнен для трёх наборов значений
переменных А и В: А — 1, В —![]()
А — —1, В = 1. Чему равна сумма полученных значений переменной С?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 4
Алгоритмические конструкции
Вариант З
А1. Дан фрагмент схемы алгоритма.
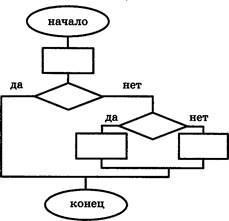
Укажите верное высказывание об этом фрагменте:
1) схема содержит команду ветвления в сокращённой форме, в которую вложена команда ветвления в пол ной форме;
2) схема содержит две команды ветвления в полной форме, одна из которых вложена в другую;
З) схема содержит две команды ветвления в сокращённой форме, одна из которых вложена в другую;
4) схема содержит команду ветвления в полной форме, в которую вложена команда ветвления в сокращённой форме;
5) ни одно из высказываний не является верным.
А2. Дан алгоритм, схема которого изображена на рисунке ниже. При каких наборах начальных значений х, у и 2, перечисленных ниже, тело цикла будет исполняться ровно З раза?
![]()
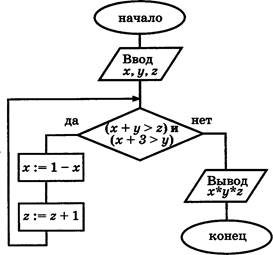
В1. На рисунке изображён алгоритм.
Определите, сколько раз в этом фрагменте будет исполняться тело цикла.
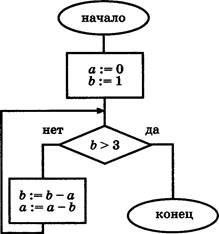
В2. Найдите значение переменной а после исполнения алгоритма, схема которого изображена на рисунке.
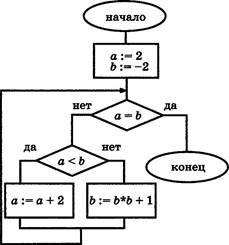
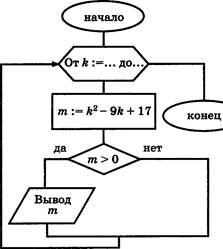
ВЗ. Дан алгоритм, схема которого изображена на рисунке.
4—Гейв. Тесты. 10 кл.
В заголовке цикла «От К : . до ... » стёрты границы изменения переменной К. Однако имеются результаты работы этого алгоритма было напечатано три числа: З; З; 9. В бланке ответов запишите через запятую границы изменения К.
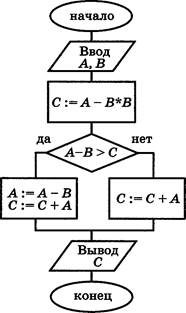
М. Дан алгоритм, схема которого изображена на рисунке.
Алгоритм был исполнен для трёх наборов значений переменных А
и В: А — 1, В —![]()
А = —1; В = 1. Чему равна сумма полученных значений переменной С?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
тест 4 |
|
|||||
|
|
|
|||||
Алгоритмические конструкции
Вариант 4
М. На рисунке изображён фрагмент схемы алгоритма.
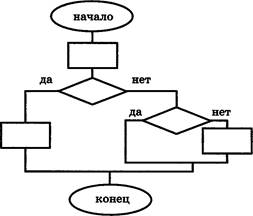
Укажите верное высказывание об этом фрагменте: 1) схема содержит команду ветвления в сокращённой форме, в которую вложена команда ветвления в полной форме;
2) схема содержит две команды ветвления в полной форме, одна из которых вложена в другую;
З) схема содержит две команды ветвления в сокращённой форме, одна из которых вложена в другую;
4) схема содержит команду ветвления в полной форме, в которую вложена команда ветвления в сокращённой форме;
5) ни одно из высказываний не является верным.
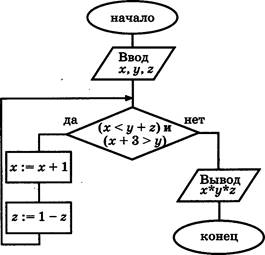
А2. Дан алгоритм, схема которого изображена на рисунке. При каких наборах начальных значений х, у и z, перечисленных ниже, тело цикла будет исполняться ровно З раза?
![]()
В1. На рисунке изображён алгоритм.
Определите, сколько раз в этом фрагменте будет ис полняться тело цикла.
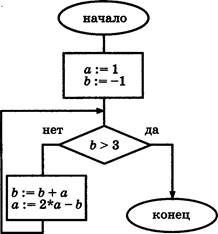
В2. Найдите значение переменной а после исполнения алгоритма, схема которого изображена на рисунке.
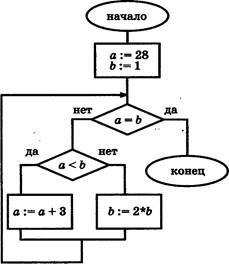
ВЗ. Дан алгоритм„ схема которого изображена на рисунке.
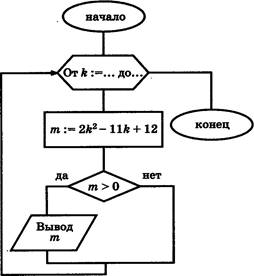
В заголовке цикла «От К : = ... до ... » стёрты границы изменения переменной К. Однако имеются результаты работы этого алгоритма было напечатано два числа: З и 7. В бланке ответов запишите через запятую границы изменения К.
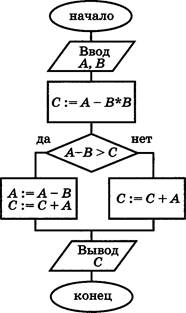
В4. Дан алгоритм, схема которого изображена на рисунке.
Алгоритм был исполнен для трёх наборов значений переменных А
и В: А = 1, В![]()
А — —1, В — 1. Чему равна сумма полученных значений переменной С?
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
|
|
вз |
|
|
|
|
|
|
|
|
Тест 5
Вспомогательные алгоритмы и рекурсия
Вариант 1
В заданиях этого теста используются вспомогательные алгоритмы в форме алгоритма-функции (процедуры). Запись этой конструкции оформлена следующим образом:
Алгоритм Имя (тип: переменная,
переменная, тип тип: переменная, .![]()
{ действие;
действие;
В скобках после имени перечислены формальные аргументы алгоритма-функции с указанием их типов, в конце указывается тип результата.
Вызов алгоритма-функции оформляется командой присваивания:
а : — Имя (выражение, выражение, ...).
А1. Ниже приведены тексты алгоритма А и алгоритма-функции В.
Алгоритм А
![]()
{ Запросить х;
Запросить у;
Делать пока ((х > 1) И (у > 1))
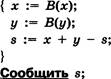
Алгоритм В (дед: х): цед
![]() дедах» Q.r :
дедах» Q.r :
{ Реди (х mod — О) то
![]()
На запросы алгоритма А для х было введено число 45, а для у — число 36. Укажите, какое число было сообщено после исполнения алгоритма А.
![]() 4)
23;
4)
23;
5) другое число, нежели указанные.
А2*. Ниже приведены тексты алгоритма М и алгоритма-функции SQ. Алгоритм М
{ Запросить п;
Сообщить п;
![]() Алгоритм х): цел { Если (х 10) иначе { SQ SQ(x
div 10) + (х mod 10)*(х mod 10); }
Алгоритм х): цел { Если (х 10) иначе { SQ SQ(x
div 10) + (х mod 10)*(х mod 10); }
Для какого из указанных ниже значений п число, которое сообщит алгоритм М после завершения работы, окажется наименьшим?
![]() 3) п - 7; 4) п - 9; 5) п - 11.
3) п - 7; 4) п - 9; 5) п - 11.
В1. Ниже приведены тексты алгоритма С и алгоритмов-функций А и В. Алгоритм С цед: К, т, п;
делать Q.r![]()
{ 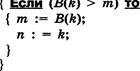 Ееди (цк) > т)
Ееди (цк) > т)
Сообщить п;
Алгоритм В (цед; х): цел
![]()
![]() дедах»
Q.r К 1 до
дедах»
Q.r К 1 до
{ Если (А(х, К) —
Алгоритм А (цед х, у): цед цед: К;
![]()
Делать К![]()
{ А := (А*у) mod (х + 1);
Какое число будет сообщено в результате исполнения алгоритма С?
В2. Ниже приведён текст алгоритма А, при исполнении которого используется алгоритм-функция В.
Алгоритм А цед: т, х, у; { Запросить т;


Алгоритм А был исполнен при т, равном З, 5, и 7. Укажите, при каком из этих трёх значений был сообщён наименьший результат.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

тест 5
Вспомогательные алгоритмы и рекурсия
Вариант 2
В заданиях этого теста используются вспомогательные алгоритмы в форме алгоритма-функции (процедуры). Запись этой конструкции оформлена следующим образом:
Алгоритм Имя (тип: переменная, переменная, ...): тип тип: переменная, ;
{ действие;
В скобках после имени перечислены формальные аргументы алгоритма-функции с указанием их типов, в конце указывается тип результата.
Вызов алгоритма-функции оформляется командой присваивания:
а е.— Имя (выражение,
выражение,![]()
А 1. Ниже приведены тексты алгоритма А и алгоритма-функции В.
Алгоритм А
![]()
{ Запросить х;
Запросить у;
Делать пока ((х > 1) и (у > 1))
![]()
Дедах» пока (х mod К > 0)
![]()
На запросы алгоритма А для х было введено число 120, а для у — число 90. Укажите, какЬе число б€ило сообщено после исполнения алгоритма А.
5) другое число, нежели указанные.
А2*. Ниже приведены тексты алгоритма М и алгоритма-функции PQ.
Алгоритм М
![]() Запросить
п;
Запросить
п;
Делать пока (PQ(n) > 13) ![]() п PQ(n);
п PQ(n);
Сообщить п;
Алгоритм Рацед; х): цед
{ Еели (х < 10) r.Q { PQ х
+ 2; } иначе PQ PQ(x div ![]() mod 10));
mod 10)); ![]()
Для какого из указанных ниже запрашиваемых значений п число, которое сообщит алгоритм М после завершения работы, окажется наименьшим?
1) 121;
4) п — 181;
2) п - 161; ![]() 5) п = 191.
5) п = 191.
В1. Ниже приведены тексты алгоритма С и алгоритмов-функций А и В.
Алгоритм С цел: к, т;
Делать К :![]()
{ Ечм (ЦК) т) r.Q { т :![]()
Сообщить т;
Алгоритм В (вед; д): цед цел: К;
![]()
дедах» Q.r К :— 1 до х шагом 2
{ Ечм (А(х,
Ь) > 1) В + К; ![]() иначе { В В — 1; }
иначе { В В — 1; }
Алгоритм А (мед; х, у): цед { дедах» пока (не
(х — у)) { Если (х > у) { х : ![]() ицау.е { У :
ицау.е { У :![]()
Какое число будет сообщено в результате исполнения алгоритма С?
В2. Ниже приведён текст алгоритма А, при исполнении которого используется алгоритм-функция В.
Алгоритм А цед: т, х, у; { Запросить т;


Алгоритм А был исполнен при т, равном З, 5, и 7. Укажите, при каком из этих трёх значений, был сообщён наименьший результат.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
вед |
|
|
|
|
|
|
|
|
Тест 5 |
|
||||
|
|
|
||||
Вспомогательные алгоритмы и рекурсия
Вариант З
В заданиях этого теста используются вспомогательные алгоритмы в форме алгоритма-функции (процедуры). Запись этой конструкции оформлена следующим образом:
Алгоритм Имя (тип: переменная,
переменная, ...): тип тип : переменная, .![]()
В скобках после имени перечислены формальные аргументы алгоритма-функции с указанием их типов, в конце указывается тип результата.
Вызов алгоритма-функции оформляется командой присваивания:
а Имя (выражение, выражение![]()
А1. Ниже приведены тексты алгоритма А и алгоритма-функции В.
Алгоритм А
![]()
{ Запросить х;
Запросить у;
Дедах» пока «х > 1) ц (у > 1))
{ х В(х);
(дед:
![]()
Делать :
![]() { Если
(х mod К
{ Если
(х mod К
На запросы алгоритма А для х было введено число 36, а для у — число 20. Укажите, какое число было сообщено после исполнения алгоритма А.
2) 25; 3) 46; 4) 47;
5) другое число, нежели указанные.
А2*. Ниже приведены тексты алгоритма М и алгоритма-функции SQ.
Алгоритм М цел: п;
{ Запросить п;
Делать пока (SQ(n) > 7) ![]() п SQ(n);
п SQ(n);
Сообщить п;
Алгоритм SQ (цед: х): цед
{ Если (х < 10)
иначе
{ SQ SQ(x div 10) + (х mod 10)*(х mod 10); }
Для какого из указанных ниже запрашиваемых значений п алгоритм М сообщит наибольшее число?
1) п = 7; 2) п - 11; 3) п - 13; 4) п - 17; 5) п - 21.
В1. Ниже приведены тексты алгоритма С и алгоритмов-функций А и В.
Алгоритм С цед: К, т, п;
![]()

Сообщить п;
Алгоритм В (цед: х): цед
![]()
Делать от К : 1 до х шагом 2
{ Если
К) — 1) то в в + 1; ![]()
Алгоритм А (цед: х,. у): цед
![]()
Делать QI К :![]()
{ А (А*у) mod (х. + 1);
Какое число будет сообщено в результате исполнения алгоритма С?
В2. Ниже приведён текст алгоритма А, при исполнении которого используется алгоритм-функция В.
Алгоритм А цел: т, х, у;
{ Запросить т;
пока (х < т)
![]()
Если (В(у) ![]() у) то
у) то
![]()
![]() х div у;
х div у;
Сообщить у*х;
5-
Гейн. Тесты. 10 кл.

Алгоритм А был исполнен при т, равном З, 5, и 7. Укажите, при каком из этих трёх значений был сообщён наибольший результат.
Бланк ответов
Фамилия, имя ![]()

Тест 5
Вспомогательные алгоритмы и рекурсия
Вариант 4
В заданиях этого теста используются вспомогательные алгоритмы в форме алгоритма-функции (процедуры). Запись этой конструкции оформлена следующим образом:
Алгоритм Имя (тип: переменная, переменная, тип тип : переменная, ;
{ действие; действие;
В скобках после имени перечислены формальные аргументы алгоритма-функции с указанием их типов, в конце указывается тип результата.
Вызов алгоритма-функции оформляется командой присваивания:
а е.— Имя (выражение, выражение, е..).
А1. Ниже приведены тексты алгоритма А и алгоритма-функции В.
Алгоритм А
![]()
{ Запросить х;
Запросить у;
Делать пока ((х > 1) щ (у >
1)) { х :![]()
у .— е у / В(у);
![]()

На запросы алгоритма А для х было введено число 90, а для у — число 420. Укажите, какое число было сообщено после исполнения алгоритма А.
2) 25; 4) 32;
5) другое число, нежели . указанные.
А2*. Ниже приведены тексты алгоритма М и алгоритма-функции PQ.
Алгоритм М
{ Запросить п;
Делать пока (PQ(n) > 13)
{ п := PQ(n);
Алгоритм Р¶цед: х): цед ![]() Если (х < 10) r.Q PQ х + З;
Если (х < 10) r.Q PQ х + З; ![]() иначе { PQ PQ(x div
иначе { PQ PQ(x div ![]() mod 10));
mod 10)); ![]()
Для какого из указанных ниже запрашиваемых значений п число, которое сообщит алгоритм М после завершения работы, окажется наименьшим?
|
1) п - 121; |
2) - 161; |
|
|
4) п - 181; |
5) п - 191. |
|
В1. Ниже приведены тексты алгоритма С и алгоритмов-функций А и В.
Алгоритм С
![]() — 9 до 12
— 9 до 12
![]() Если (ЦК) > т) то т ЦК);
Если (ЦК) > т) то т ЦК); ![]()
Сообщить т;
Алгоритм В (цед: х): цед
![]()
Делать от к :- 1 до х !Щщ.п.М 2 ![]() Ееди (АС, х) > 1) то { в в + 1;
Ееди (АС, х) > 1) то { в в + 1; ![]() иначе { В В — 1;
иначе { В В — 1; ![]()
Алгоритм А (цед: х, у): цед {
делать пока (це (х = у» { Если (х > у) { х :![]()
![]()
Какое число будет сообщено в результате исполнения алгоритма С?
В2. Ниже приведён текст алгоритма А, при исполнении которого используется алгоритм-функция В.
Алгоритм А
цед: т, х, у;
{ Запросить т;
пока (х < т)
![]()
Если (В(у) > у) то
![]()
Сообщить у + х;

Алгоритм А был исполнен при т, равном З, 5, и 10. Укажите, при каком из этих трёх значений был сообщён наибольший результат.
Бланк ответов
Фамилия, имя Класс

Тест 6
Обработка массивов
Вариант 1
А1. Дан алгоритм, схема которого изображена на рисунке.
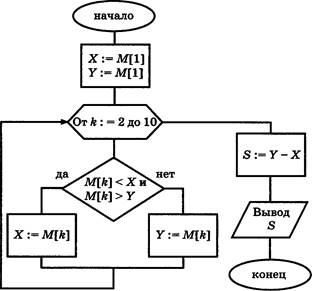
Этот алгоритм был исполнен для массива М, описанного следующей таблицей:
|
1,2 |
-0,5 |
3,6 |
|
1 |
-0,1 |
о |
з |
О |
з |
После исполнения сообщено число:
![]()
5) другое число, нежели указанные.
А2. Дан фрагмент программы, обрабатывающей двумерный массив А размером п><п.
|
Паскаль |
for i : 1 to п div 2 do for ј 1 to п do begin
end; |
|
Бейсик |
FOR i - 1 ТО FOR Ј = i ТО п с = A(i, .Ј) A(i, ј) = А(п — i + 1, З)
NEXT .i NEXT i |
|
Алгоритмический язык |
|
Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, Л величина i является номером строки, а величина ј — номером столбца, в котором расположен элемент. Тогда данный алгоритм:
1) отражает эту таблицу симметрично относительно вертикальной оси симметрии квадрата;
2) отражает эту таблицу симметрично относительно горизонтальной оси симметрии квадрата;
З) отражает эту таблицу симметрично относительно диагонали, идущей из левого верхнего угла в правый нижний;
4) отражает эту таблицу симметрично относительно диагонали, идущей из правого верхнего угла в левый нижний;
5) отражает эту таблицу иным способом, не совпадающим ни с одним из указанных.
В1. Значения элементов двумерного целочисленного массива В, оба индекса которого меняются в пределах от 1 до 11, задаются с помощью двойного цикла, представленного следующим фрагментом программы:
|
Паскаль |
вд,1] 1; for К 1 to 11 do for п :— К to 11 do begin if (п > 1) then ЧК, п] := п*К — ВЕК, п во, К] ЧК, п]; end; |
|
|
Бейсик |
ва,1) - 1 FOR К - 1 ТО 11 FOR п - К ТО 11
THEN ЩК, п) -— п*К — мк, п - 1) во, К) - мк, п) NEXT п NEXT К |
|
|
Алгоритмический язык
|
Делать QI К :
{ Если (п > 1) то
|
|
Сколько в этом массиве окажется чётных чисел?
В2*. Первоначально все элементы двумерного массива А размером 2n><2n равны О. Этот массив обрабатывается в следующем фрагменте программы:
|
Паскаль |
for i 1 to п do — i to 2*i do begin
end; for i 1 to 2*n do for • 1 to п do — О then К |
Продолжение
|
Бейсик |
FOR i - 1 ТО п FOR = i ТО АО, i) — А(ј, i) NEXT Ј NEXT i FOR i - 1 ТО FOR • = 1 то п ТНТ•.Ј К- К+1 NEXT Ј NEXT i |
— 1 |
|
|
Алгоритмический
язык
|
Делать от i :— { Делать QI .ј : { Если A[i, Л : |
i до
|
1;
|
Какое значение будет иметь переменная после окончания работы указанного фрагмента программы? Ответ запишите выражением, зависящим от п. Если при чётных и нечётных значениях К выражения получаются различными, запишите их, отделив друг от друга точкой с запятой (сначала выражение для нечётных значений К, а затем для чётных).
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

|
Тест 6 |
|
Обработка массивов
Вариант 2
А1. Дан алгоритм, схема которого изображена на ри сунке.
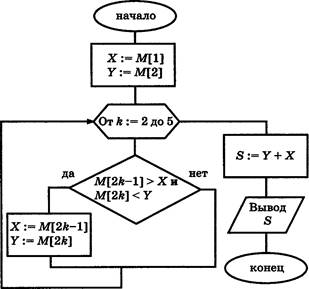
Этот алгоритм был исполнен для массива М, описанного следующей таблицей:
|
1,2 |
0,7 |
1,6 |
-0,8 |
-1 |
2,1 |
|
|
|
|
После исполнения сообщено число:
5) другое число, нежели указанные.
А2. Дан фрагмент программы, обрабатывающей двумерный массив А размером п><п, где п > 2.
|
Паскаль |
for i :— 1 to п — 1 do — i + 1 to п do begin
end; |
|
Бейсик |
FOR i - 1 ТО п - 1 FOR Ј - i + 1 ТО п с — АО, Ј) A(i, ј) = АО, i)
NEXT .i NEXT i |
|
Алћоритмический язык
|
|
Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, Л величина i является номером строки, а величина ј — номером столбца, в котором расположен элемент. Тогда данный алгоритм:
1) отражает эту таблицу симметрично относительно вертикальной оси симметрии квадрата;
2) отражает эту таблицу симметрично относительно горизонтальной оси симметрии квадрата;
З) отражает эту таблицу симметрично относительно диагонали, идущей из левого верхнего угла в правый нижний;
4) отражает эту таблицу симметрично относительно диагонали, идущей из правого верхнего угла в левый нижний;
5) отражает эту таблицу иным способом, не совпадающим ни с одним из указанных.
![]() В1. Значения элементов двумерного
целочисленного массива В, оба индекса которого меняются в пределах от 1 до 12,
задаются с помощью двойного цикла, представленного следующим фрагментом
программы:
В1. Значения элементов двумерного
целочисленного массива В, оба индекса которого меняются в пределах от 1 до 12,
задаются с помощью двойного цикла, представленного следующим фрагментом
программы:
|
Паскаль
|
for К 2 to 12 do for п : 1 to К do begin
end; |
|
|
|
ва,1) = 1 FOR К = 2 ТО 12 FOR п - 1 ТО К МК, п) - - В(К-1, п) во, К) - мк, п) NEXT п NEXT К |
|
|
АЈЁ'орит*йчесКий язык |
Делать от : { дедах.» п ВЕК, п] - ВО, ВЕК, п]; |
|
Сколько в этом массиве окажется чётных чисел?
В2*. Первоначально все элементы двумерного массива А размером 2n><2n равны О. Этот массив обрабатывается в следующем фрагменте программы:
|
Паскаль |
for i п+1 to 2*n do for .Ј • — 2*n+1 — i to i do begin
end; to 2*n do
|
Продолжение
|
|
FOR i - п+1 ТО R ј — 2*п+1 АО, ј) — Аб, АО, i) = АО NEXT Ј NEXT i FOR i - 1 ТО FOR • - 1 то THEN К- К+1 NEXT Ј NEXT i |
- i ТО i |
|
|
«Алгоритмический язык |
Делать QI • п+1 2*п
|
||
Какое значение будет иметь переменная К после окончания работы указанного фрагмента программы? Ответ запишите выражением, зависящим от п. Если при чётных и нечётных значениях К выражения получаются различными, запишите их, отделив друг от друга точкой с запятой (сначала выражение для нечётных значений К, а затем для чётных).
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 6
Обработка массивов
Вариант З
А1. Дан алгоритм, схема которого изображена на рисунке.
![]()
|
х ща |
Этот алгоритм был исполнен для массива М, описанного следующей таблицей:
|
1,2 |
-0,7 |
1,6 |
1,8 |
1 |
2,1 |
2,9 |
|
|
-0,9 |
После исполнения сообщено число:
![]()
5) другое число, нежели указанные.
А2. Дан фрагмент программы, обрабатывающей двумерный массив А размером п><п.
|
Паскаль |
for i е.— 1 to п — 1 do begin
— 1 to т do begin a[i, ј] а[К, т); end; end; |
а[К, т] : |
|
Бейсик |
FOR i - 1 ТО п - 1 FOR
АО, ј) — А(К, т) А(К, т) — NEXT Ј NEXT i |
|
|
Алгоритмический язык |
A[i, Л е.— А[К, т); |
|
Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, Л величина i является номером строки, а величина .ј номером столбца, в котором расположен элемент. Тогда данный алгоритм:
1) отражает эту таблицу симметрично относительно вертикальной оси симметрии квадрата;
2) отражает эту таблицу симметрично относительно горизонтальной оси симметрии квадрата;
З) отражает эту таблицу симметрично относительно диагонали, идущей из левого верхнего угла в правый нижний;
4) отражает эту таблицу симметрично относительно диагонали, идущей из правого верхнего угла ц левый нижний;
5) отражает эту таблицу иным способом, не совпадающим ни с одним из указанных.
В1. Значения элементов двумерного целочисленного массива В, оба индекса которого меняются в пределах от 1 до 11, задаются с помощью двойного цикла, представленного следующим фрагментом программы:
|
Паскаль |
for К 1 to 11 do for п
end; |
|
Бейсик |
ва,1) - 2 FOR К - 1 ТО 11 FOR п - К ТО 11
ТНТ..Ј мК, п) — п*К — мк, п - 1) во, К) - В(К, п) NEXT п NEXT К |
|
Алгоритмический язык
|
|
Сколько в этом массиве окажется нечётных чисел?
В2*. Первоначально все элементы двумерного массива А размером 2пХ2п равны О. Этот массив обрабатывается в следующем фрагменте программы:
|
Паскаль
|
for i :— п+1 to 2*n do = i div 2 to i do begin
end;
= 1 to 2*n do if A[i,
ј] О then К |
б—Гейн. Тесты. 10 кл.
Продолжение
|
Бейсик
|
FOR i = п+1 ТО FOR АО, i) — АО, i) - 1 NEXT .Ј NEXT i
FOR i - 1 ТО - 1 то IF Аб, Ј) - О ТНТЧ К- К+1 NEXT Ј NEXT i |
|
Алгоритмический язык
|
делать от i :— п+1 да 2*п {
{ Делать от ј 1 Если (АР, Л : |
Какое значение будет иметь переменная К после окончания работы указанного фрагмента программы? Ответ запишите выражением, зависящим от п. Если при чётных й нечётных значениях К выражения получаются различными, запишите их, отделив друг от друга точкой с запятой (сначала выражение для нечётных значений К, а затем для чётных).
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 6
Обработка массивов
Вариант 4
А 1. Дан алгоритм, схема которого изображена на рисунке.
![]()
|
У МПО] |
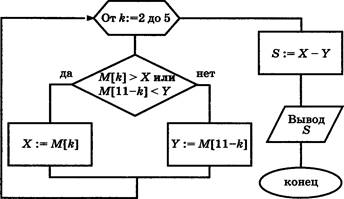
Этот алгоритм был исполнен для массива М, описанного следующей таблицей:
|
1,2 |
-0,7 |
1,6 |
1,8 |
-1 |
2,1 |
-0,9 |
о |
-0,5 |
0,9 |
После исполнения сообщено число:
![]()
5) другое число, нежели указанные.
А2. Дан фрагмент программы, обрабатывающей двумерный массив А размером п><п, где п 2.
|
Паскаль |
с : end; |
|
Бейсик |
FOR .Ј - 1 ТО пр FOR i - 1 ТО п с = A(i, Ј) A(i, Ј) —
АО, п АО, п NEXT .i NEXT i |
|
Алгорйтмический язык |
|
Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, Л величина i является номером строки, а величина .i — номером столбца, в котором расположен элемент. Тогда данный алгоритм:
1) отражает эту таблицу симметрично относительно вертикальной оси симметрии квадрата;
2) отражает эту таблицу симметрично относительно горизонтальной оси симметрии квадрата;
З) отражает эту таблицу симметрично относительно диагонали, идущей из левого верхнего угла в правый нижний;
4) отражает эту таблицу симметрично относительно диагонали, идущей из правого верхнего угла в левый нижний;
5) отражает эту таблицу иным способом, не совпадающим ни с одним из указанных.
В1. Значения элементов двумерного целочисленного массива В, оба индекса которого меняются в пределах от 1 до 12, задаются с помощью двойного цикла, представленного следующим фрагментом программы:
|
Паскаль |
for К :— 2 to 12 do for п : 1 to К do begin ЧК, п] - В[К-1, п] В[п, К] ВЕК, end; |
|
|
Бейсик |
ва,1) = 2 FOR К = 2 ТО 12 FOR п = 1 ТО К мК, п) - - В(К-1, п) во, К) - щк, п) NEXT п NEXT К |
|
|
Алгоритмический я;щк
|
ВЕК, п] ВО, |
|
Сколько в этом массиве окажется нечётных чисел?
В2*. Первоначально все элементы двумерного массива А размером 2n><2n равны О. Этот массив обрабатывается в следующем фрагменте программы:
|
Паскаль |
for i . — 2 to п do — i div 2 to 2*i do begin
end;
|
Продолжение
|
Бейсик
|
FOR i - 2 ТО п FOR Ј - ТО A(i, ј) — АО, ј) + 1 АО, i) — АО, i) - 1 NEXT Ј NEXT i
FOR i - 1 ТО п OR .Ј - 1 ТО THEN К- К+1 NEXT Ј NEXT i |
|
|
Алгоритмический язык |
Делать от i :— 1 { Делать от ј :—
1 Если (A[i, .jl : |
1;
|
Какое значение будет иметь переменная К после окончания работы указанного фрагмента программы? Ответ запишите выражением, зависящим от п. Если при чётных и нечётных значениях К выражения получаются различными, запишите их, отделив друг от друга точкой с запятой (сначала выражение для нечётных значений К, а затем для чётных).
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 7
Компьютерное моделирование
Вариант 1
В заданиях А2 и В2 для моделирования случайных процессов используется датчик случайных чисел. В алгоритмах он обозначен как ДСЧ(х) и генерирует случайную величину х, равномерно распределённую на отрезке [О; х].
А 1. При изучении процесса остывания стального бруска рассматривалась информационная модель, в которой факторы, влияющие на процесс (по мнению экспериментаторов), были описаны следующими параметрами:
То — начальная температура СС);
![]() — масса бруска (кг);
t — время, прошедшее от начала эксперимента (с); Т — температура бруска к
моменту времени t СС).
— масса бруска (кг);
t — время, прошедшее от начала эксперимента (с); Т — температура бруска к
моменту времени t СС).
По результатам эксперимента были построены следующие графики (точками на графиках обозначены экспериментальные данные):

2 4 6 8 10
Время Время
То— 50, т — 1,5
![]()
![]()
![]() в)г)
в)г)
10
Время Время
![]()
После изучения графиков была предложена следующая
математическая модель: Т = КЛ То, m)a t , где а ![]() некоторая
константа, меньшая 1, а К некоторый коэффициент пропорциональности, зависящий
от других факторов.
некоторая
константа, меньшая 1, а К некоторый коэффициент пропорциональности, зависящий
от других факторов.
Какой из перечисленных ниэке вариантов вида функции f(To, т) делает эту модель наиболее адекватной эксперименту?
1) лто,
т) - ктот•, ![]()
![]() 4) f(To, т) — КТО;
4) f(To, т) — КТО;
5) f(To, т) = Кт.
|
У |
у=тв
|
|
|
|
5 |
|
А2. Для подсчёта методом Монтех2 Карло площади фигуры, ограниченной параболой У =Д 16х: и окружностью с ра-
диусом 5 с центром в начале координат (см. рис.), был составлен следующий алгоритм:
Площадь фигуры
{ Запрорить К; (*К— количество точек, генерируемых случайным образом*)
Дедах.» 1 до к х дсч(8) - 4; У ДСЧ(5);
Ееди {
лт лт + 1; ![]()
S 40*N/k;
“Площадь фигуры приближённо равна”, S;
Однако в алгоритме оказалось стёртым условие в операторе ветвления. Укажите, какое условие может быть в этом операторе.
1) (у 6х2) и (х2 + у2 25);
2) (у 6х2) или (х2 + у2 25);
З) (у > 6х2) или (х2 + у2 25);
4) (у i6X2) или (х2 + уа < 25);
5) другое условие, нежели указанные.
В1. Перечислите номера пунктов, в которых указаны цели, достижимые при компьютерном моделировании ядерного взрыва. В ответе расположите номера в порядке возрастания без пробелов и знаков препинания (например, 124).
1) Прогноз влияния взрыва на окружающую среду.
2) Экспериментальная проверка влияния высокой температуры и излучения на природные объекты. З) Обеспечение безопасности людей.
4) Понижение стоимости исследований.
В2*. Наблюдения за неопознанным летающим объектом (НЛО) показали, что он движется по прямой, перемещаясь каждую секунду на одно и то же расстояние вправо или влево от той точки, где он находился в предыдущий момент времени. При этом оказалось, что, хотя выбор направления перемещения происходит случайно, частота смещения вправо в 2 раза меньше частоты смещения влево. Для компьютерного моделирования этого процесса был составлен алгоритм, который по введённому времени t сообщает, как далеко от точки, из которой началось движение НЛО, окажется объект. Какой из приведённых• ниже алгоритмов адекватно отражает процесс перемещения НЛО? В ответе перечислите через запятую номера правильных, по вашему мнению, алгоритмов; если правильного алгоритма нет, то в ответе запишите число О.
1) Алгоритм Движение_НЛО цел: i, t; вещ: s; { Запросить t;
Делать Q.r i :![]()
{ s :- + дсч(3) - 1; Сообщить abs(s);
2)
Алгоритм Движение_НЛО цед: i, t, У, вещ: х; { Запросить
t; ![]() О; делать i :
О; делать i : ![]()
![]() х
дсч(2) - 1;
х
дсч(2) - 1;
![]()
Сообщить abs(s);
З) Алгоритм Движение_НЛО мед: t, s•, вещ: х; { Запросить t;
Делать от i :— 1 ![]() х дсч(3) - 1; Если (х < О)
то { s .
х дсч(3) - 1; Если (х < О)
то { s . ![]() иначе { s :
иначе { s :![]()
Сообщить abs(s);
4) Алгоритм Движение НЛО цед: i, t, з; вещ:
х; { Запросить t; ![]() о;
о;
Делать от i 1![]()
{ х дсч(3) -
2; Еели (х О) { s ![]() иначе { s .
иначе { s .![]()
Сообщить abs(s);
5) Алгоритм Движение НЛО цел: i, t; вещ: 8', { Запросить е,
Делать от i .![]()
{ s : + дсч(3) - 2;
Сообщить abs(s);
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
|
|
|
|
|
|
Тест 7
Компьютерное моделирование
Вариант 2
В заданиях А2 и В2 для моделирования случайных процессов используется датчик случайных чисел. В алгоритмах он обозначен как ДСЧ(х) и генерирует случайную величину х, равномерно распределённую на отрезке [О; х].
А 1. При изучении процесса распространения слухов среди населения рассматривалась информационная модель, в которой факторы, влияющие на процесс (по мнению экспериментаторов), были описаны следующими параметрами:
![]() численность первично
проинформированных (чел.); р — достоверность сообщения, т. е. доля поверивших
первичной информации в общем числе проинформированных (96); t — время,
прошедшее от начала эксперимента (сут.);
численность первично
проинформированных (чел.); р — достоверность сообщения, т. е. доля поверивших
первичной информации в общем числе проинформированных (96); t — время,
прошедшее от начала эксперимента (сут.);
N — численность знающих информацию к моменту ![]() времени t
(чел.).
времени t
(чел.).
По результатам эксперимента были построены следующие графики (точками на графиках обозначены экспе-
риментальные данные):
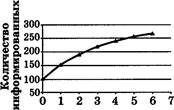
Время No 100, р 10
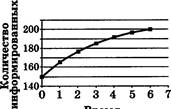
Время лто- 150, р- 50
б) 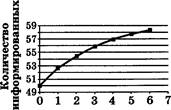
Время 50, р- 100
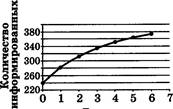
Время луо- 240, р- ЗО
После изучения графиков была предложена следующая математическая модель: лт = No + kf(No, р) (1 — at), где а — некоторая константа, меньшая 1, а К — некоторый коэффициент пропорциональности, зависящий от других факторов.
Какой из перечисленных ниже вариантов вида функции f(No, р) делает эту модель наиболее адекватной эксперименту?
|
1) f(No, р) = Тор |
2) f(No, р) = |
Р |
|
3) f(No, р)
5) f(No, р) = hNop2 |
4) f(No, р) - |
|
|
|
|
|
|
|
|
|||
|
о |
5 |
10 |
|
|
|
|||
А2. Для подсчёта методом МонтеКарло площади фигуры, ограниченной параболой у = х2 и окружностью с центром в точке с координатами (5; О) и радиусом 5 (см. рис.), был составлен следующий алгоритм:
![]() —
количество точек, генерируемых случайным образом*)
—
количество точек, генерируемых случайным образом*)
дедах»
{ х дсч(2);
У ДСЧ(4);

С.00бЩЩТ.» ”Площадь фигуры приближённо равна“, S;
Однако в алгоритме оказалось стёртым условие в операторе ветвления. Укажите, какое условие может быть в этом операторе:
1)
(у ![]() х2) и ((x — + у2 25);
х2) и ((x — + у2 25);
2)
(у ![]() х2) или ((x — + у2 25);
З) (у
х2) или ((x — + у2 25);
З) (у ![]() х2) или ((x — + у2 25);
х2) или ((x — + у2 25);
4) (у ![]() х2)
и ((x — + у2 25);
х2)
и ((x — + у2 25);
5) другое условие, нежели указанные.
![]() В1. Перечислите номера тех пунктов, в
которых указаны цели, достижимые при компьютерном моделировании влияния отлова
рыбы на её количество в море. В ответе расположите номера в порядке возрастания
без пробелов и знаков препинания (например, 124).
В1. Перечислите номера тех пунктов, в
которых указаны цели, достижимые при компьютерном моделировании влияния отлова
рыбы на её количество в море. В ответе расположите номера в порядке возрастания
без пробелов и знаков препинания (например, 124).
1) Обеспечение данными об особенностях размножения рыб данной породы.
2) Получение данных о предельно допустимых нормах отлова для того, чтобы популяция рыбы не исчезла. З) Обеспечение безопасности рыбаков при ловле рыбы. 4) Понижение стоимости исследований.
В2*. В некотором старинном замке живёт привидение. Наблюдения за ним показали, что привидение либо поёт, либо жутко смеётся, либо летает по замку. Если в некоторый момент времени привидение пребывает в некотором состоянии (т. е. поёт, смеётся или летает), то через секунду оно случайным образом переходит в одно из двух других своих состояний. При этом оказалось, что при выборе очередного состояния в состояние смеха привидение переходит в 2 раза чаще, чем в любое из двух других состояний, а в состояние пения или полёта оно переходит с одинаковой вероятностью. Для компьютерного моделирования этого процесса был составлен алгоритм, который по введённому времени t сообщает, что будет делать привидение в этот момент. Какой из приведённых ниже алгоритмов адекватно отражает процесс изменения состояний привидения, если в начальный момент оно поёт? В ответе перечислите через запятую номера правильных, по вашему мнению, алгоритмов; если правильного алгоритма нет, то в ответе запишите число О.
1) Алгоритм Привидение цед: i, t; вещ: х; сим: s; { Запросить t;
Делать от i .
{ Если (s — ”Поёт”) то х ДСЧ(3)•,
Если (х < 1) то { s : ”Летает” ; ![]() иначе { s ”Смеётся”;
иначе { s ”Смеётся”; ![]()
Если (s = ”Летает”) то
{ х ДСЧ(3)•,
Если (х < 1) то { s . ”Поёт"; ![]() иначе { s ”Смеётся”;
иначе { s ”Смеётся”; ![]()
Если (s = ”Смеётся”) r.Q
{ х ДСЧ(3)•,
Если (х < 1) то { s : = ”Поёт”; ![]() иначе { s е.— ”Летает”; }
иначе { s е.— ”Летает”; }
Сообщить з;
2) Алгоритм Привидение цед: i, t; цещ: х; сим: 8',
{ Запросить t; s :— ”Поёт”;
Делать поща (i < t)
{ Если (s — ”Поёт”) то
{ х ДСЧ(З);
Если (х < 1) то { s ”Летает”;
![]()
![]() ”Смеётся”;
”Смеётся”; ![]()
Если (s = ”Летает”) то ![]() х дсч(3);
х дсч(3);
Если (х 1) то { s :![]()
![]() ”Смеётся”;
”Смеётся”; ![]()
Если (s = ”Смеётся”) то ![]() х дсч(2)•, Если (х < 1) то
{ s •
х дсч(2)•, Если (х < 1) то
{ s • ![]() иначе { s . ”Летает”; }
иначе { s . ”Летает”; }
![]()
Сообщить .s;
З) Алгоритм
Привидение цед: i, t; вещ: х; сим: 8', { Запросить t; ![]() ”поёт”;
”поёт”;
Делать от i .![]()
{ Если (s — ”Поёт”) то
{ х дсч(3);
Если (х < 1) ![]() ”Летает”;
”Летает”; ![]() иначе { s ”Смеётся”;
иначе { s ”Смеётся”; ![]()
Если (s = ”Летает”) то ![]() х ДСЧ(З)•,
х ДСЧ(З)•,
Если (х < 1) I.Q •— ”Поёт”; ![]() иначе { s . — ”Смеётся”;
иначе { s . — ”Смеётся”; ![]()
Если (s = ”Смеётся”) то ![]() х дсч(2);
х дсч(2);
Если (х < 1) { . - ”Поёт”; ![]() иначе { s := ”Летает”;
иначе { s := ”Летает”; ![]()
Сообщить s;
4) Алгоритм Привидение цел: Г, t; вещ: х; сим: s;
{ Запросить t; s :—
”Поёт”; ![]() о;
о;
Делать пока (i t)
{ Если (s = ”Поёт”) И (i <
t) то ![]() х дсч(2);
х дсч(2);
Если (х < 1) то { s ”Летает”; ![]() иначе { s . ”Смеётся”;
иначе { s . ”Смеётся”; ![]()
![]()
Если (s = ”Летает”) и (i < t) то ![]() х дсч(2);
х дсч(2);
Ееди (х 1) то { : ”Поёт”•, ![]()
![]() иначе { s ”Смеётся”;
иначе { s ”Смеётся”; ![]()
Если (s = ”Смеётся”) и (i t) то { х ДСЧ(3)•,
Если (х < 1) r.Q { s • ”Поёт”; } иначе { s ”Летает”; }
Сообщить s;
5) Игоритм Привидение цед: i, t; вещ: х; сим: з; { Запросить t;
”Поёт”;
Делать от i 1 до t
{ Если (8 — ”Поёт”) то х дсч(3);
Если (х < 1) то { s о— ”Летает”; ![]() — ”Смеётся”;
— ”Смеётся”; ![]()
иначе
(Если (8 = ”Летает”) то
{ х ДСЧ(3)•,
Если (х < 1) то { s ”Поёт”; ![]() иначе { s . ”Смеётся” ;
иначе { s . ”Смеётся” ; ![]()
иначе
{ Если (s = ”Смеётся”) то { х дсч(2);
Если (х < 1) то { s .
![]() иначе { s . ”Летает”;
иначе { s . ”Летает”;
Сообщить з;
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
|
|
|
|
|
|
Тест 7
Компьютерное моделирование
Вариант З
В заданиях А2 и В2 для моделирования случайных процессов используется датчик случайных чисел. В алгоритмах он обозначен как ДСЧ(х) и генерирует случайную величину х, равномерно распределённую на отрезке [О; х].
М. При изучении популяции гусениц тутового шелкопряда рассматривалась информационная модель, в которой существенные факторы (по мнению экспериментаторов) были описаны следующими параметрами:
![]() — начальная масса гусениц (кг);
— начальная масса гусениц (кг);
![]() — время, прошедшее от начала
эксперимента (сут.);
— время, прошедшее от начала
эксперимента (сут.); ![]() — масса гусениц к моменту времени t (кг).
— масса гусениц к моменту времени t (кг).
По результатам эксперимента были построены следующие графики (точками на графиках обозначены экспериментальные данные):
 6)
6) 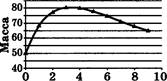
Время Время то — 100
в)  г)
г)
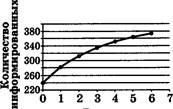
Время Время то — 150 No- ИО, р- ЗО
После изучения графиков была предложена следующая математическая модель: т то + bf(mo, t)a t , где а некоторая константа, меньшая 1, а некоторый коэффициент пропорциональности, зависящий от других факторов.
7—Гейн. Тесты. 10 кл.
Какой из перечисленных ниже вариантов вида функции f(mo, t) делает эту модель наиболее адекватной эксперименту?
1) f(mo, t) =
kmot•, ![]()
З) f(mo, t) = Кт; 4) f(mo, t) = kt;
5) f(mo, t) = .eRt.
![]() у 0,5х2
у 0,5х2
А2. Для подсчёта методом Монте-Карло площади фигуры, ограниченной параболой у = 0,5х2 и окружностью с центром в точке с координатами (4; З) и радиусом 5 (см. рис.), был составлен слех дующий алгоритм:
Алгоритм Площадь фигуры
![]() 1, К, N; вещ: х, у, S;
1, К, N; вещ: х, у, S;
К; (*К — количество точек, генерируемых слумаЙНЫМ образом*)
1 до К
{ х ДСЧ(5) - 1;
У := ДСЧ(8)•,

СОО.бЩИ.!Ь “Площадь фигуры приближённо равна", S;
Однако в нём оказалось стёртым условие в операторе ветвления. Укажите, какое условие может быть в этом операторе:
![]() 1) (у 0,5х2) и ((х — + 2)
(у > 0,5х2) и ((х — + (у - З) (у < 0,5х2) или ((x
1) (у 0,5х2) и ((х — + 2)
(у > 0,5х2) и ((х — + (у - З) (у < 0,5х2) или ((x
4) (у 0,5х2) и ((x —
5) другое условие, нежели указанные.
В1. Перечислите номера тех пунктов, в которых указаны цели, достижимые при компьютерном моделировании полёта нового самолёта. В ответе расположите номера в порядке возрастания без пробелов и знаков препинания (например, 124).
1) Экспериментальная проверка управляемости самолёта при различных режимах полёта.
2) Повышение уровня безопасности лётчика-испытателя,
З) Прогноз поведения самолёта в различных атмосферных условиях.
4)
Понижение стоимости исследований. ![]()
В2*. На школьном балу одна из девушек — большая любительница танцев — каждый танец танцевала с одним из трёх юношей: Витей, Колей или Петей. Чтобы никого не обидеть, она каждый следующий танец танцевала с новым партнёром. При этом оказалось, что, хотя выбор юнощи на следующий танец происходил, как ей казалось, случайно, с Колей она танцевала в полтора раза чаще, чем с Витей и Петей, а вот между Витей и Петей предпочтений не наблюдалось. Для компьютерного моделирования этого процесса был составлен алгоритм, который по введённому номеру танца N сообщает, с кем танцует девушка. Какой из приведённых ниже алгоритмов адекватно отражает процесс смены партнёров по танцам, если первый танец девушка танцевала с Петей? В ответе перечислите через запятую номера правильных, по вашему мнению, алгоритмов; если правильного алгоритма нет, то в ответе запишите число О.
1) Алгоритм Выбор_партнёра_по танцу
![]()
{ Запросить
N; s ”Петя”; Делать от i :— 1![]()
{ Если (s = ”Петя”) IQ { х дсч(5);
|
Если (х < З) то {
Если (8 — ”Витя”) то { х дсч(5); |
|
|
Если (х < 2) то { s |
”Коля”;
|
Если (s — ”Коля”) ![]() х дсч(4);
х дсч(4);
Если (х 2) то { ”Петя”; ![]()
![]() { s ”Витя”;
{ s ”Витя”; ![]()
Сообщить s;
2) Алгоритм Выбор партнёра_по танцу .це.Д: ![]() х ; сим:
х ; сим:![]()
{ Запросить N; s := ”Петя”;
Дедах» пока (i < t)
{ Если (s — ”Петя”) то ![]() х дсч(5);
х дсч(5);
Если (х < 3) r.Q •— ”Коля”;
![]() иначе { s ”Витя”;
иначе { s ”Витя”; ![]()
Если (s — ”Витя”) то ![]() х дсч(5);
х дсч(5);
Если (х < 3) { ”Коля”; ![]() иначе { s . ”Петя”;
иначе { s . ”Петя”; ![]()
![]()
|
Если (s — ”Коля”) r.Q |
|
|
Если (х < 1) то { s |
”Петя”; |
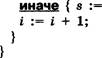 ”Витя”; }
”Витя”; }
Сообщить з;
З) Алгоритм Выбор_партнёра_по_танцу цел: i, N; цещ: х; сим: s;
{ Запросить N; s ”Петя”;
![]() Делать от i 1 до лт
Делать от i 1 до лт ![]() х дсч(10)•, Если (s — ”Петя”) то
х дсч(10)•, Если (s — ”Петя”) то
{ Если (х 6) то { s ![]() ”Коля
”Коля ![]() иначе { s .
иначе { s . ![]()
иначе
{ Если (8 = ”Витя”) IQ
{ Если (х < 6) r.Q { s ![]() ”Коля
”Коля ![]()
![]() ”Петя”;
”Петя”;
иначе
{ Если (х < 5) r.Q { s![]() ”Петя”;
”Петя”; ![]() иначе { ”Витя”;
иначе { ”Витя”; ![]()
Сообщить з;
4) Алгоритм Выбор партнёра_по танцу
![]() х ; сим: s ;
х ; сим: s ;
{ Запросить N; s :— ”Петя”;
![]() О;
О;
Делать пока (i < t) ![]() х дсч(10);
х дсч(10);
Если (s = ”Петя”) И (i < t) r.Q
{ Если (х 6) то { 8 ”Коля![]()
![]() — ”Витя”;
— ”Витя”;
Реди (8 - ”Витя”) И (i < t) r.Q
{ Если (х 6) r.Q { s ”Коля”; ![]()
![]() ”Петя";
”Петя"; ![]()
Если (8 - ”Коля”) И О < О r..Q
{ Если (х 5) r.Q { :— ”Петя”; ![]()
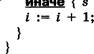 иначе { s : ”Витя”;
иначе { s : ”Витя”; ![]()
Сообщить 8',
5) Алгоритм Выбор партнёра_по танцу
цед: i, N; цещ: х; СИМ: s;
{ Запросить N; s :—
деда» пока (i < t)
{ Если (s = ”Петя”) щ (i < t) то х дсч(5);
Если (х 3) •— ”Коля ![]() иначе { s . — ”Витя”;
иначе { s . — ”Витя”; ![]()
Если (s = ”Витя”) И (i < t) то х дсч(5)•,
Если (х З) то { s ”Коля”; ![]() иначе { s ”Петя”;
иначе { s ”Петя”; ![]()
Если (s = ”Коля”) И (i t) то х дсч(2);
Если (х 1) то { s . — ”Петя”; ![]() иначе s :— ”Витя”;
иначе s :— ”Витя”;
Сообщить з;
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 7
Компьютерное моделирование
Вариант 4
В заданиях А2 и В2 для моделирования случайных процессов используется датчик случайных чисел. В алгоритмах он обозначен как ДСЧ(х) и генерирует случайную величину х, равномерно распределённую на отрезке [О; х].
А1. При изучении влияния рекламы на спрос рассматривалась информационная модель, в которой существенные факторы (по мнению экспериментаторов) были описаны следующими параметрами:
К — количество мест, в которых размещалась реклама (шт.); ![]() уровень
продаж до начала рекламной акции (тыс. руб.);
уровень
продаж до начала рекламной акции (тыс. руб.);
![]() — время, прошедшее от начала эксперимента
(сут.); s — уровень продаж к моменту времени t (тыс. руб.). По результатам
эксперимента были построены следующие графики (точками на графиках обозначены
экспериментальные данные):
— время, прошедшее от начала эксперимента
(сут.); s — уровень продаж к моменту времени t (тыс. руб.). По результатам
эксперимента были построены следующие графики (точками на графиках обозначены
экспериментальные данные):
![]()
![]()
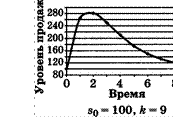 Время
Время
![]()
![]() Время
Время
„о- 240, к- 16
После изучения графиков была предложена следующая математическая модель: s = .so + f(so, К, t)at , где а — некоторая константа, меньшая 1.
Какой из перечисленных ниже вариантов вида функции f(so, К, t) делает эту модель наиболее адекватной эксперименту?
![]() А2. Для подсчёта методом МонтеКарло площади фигуры,
ограниченной параболой у = х2 и окружностью с центром в точке с
координатами (О; 5) и радиусом 5 (см. рис.), был составлен следующий алгоритм:
А2. Для подсчёта методом МонтеКарло площади фигуры,
ограниченной параболой у = х2 и окружностью с центром в точке с
координатами (О; 5) и радиусом 5 (см. рис.), был составлен следующий алгоритм:
АДЕ92И.тм Площадь фигуры цед; 1, К, N; цещ: х, у, S;
{ 3a0P.Q9M.r.» К; (*К — количество точек, генерируемых случайным образом *)
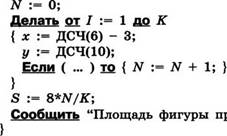 ”Площадь фигуры приближённо равна”, S;
”Площадь фигуры приближённо равна”, S;
Однако в алгоритме оказалось стёртым условие в операторе
ветвления. Укажите, какое условие может быть в ![]() этом операторе:
этом операторе:
1) (у х2) и ((у — + 25); 2) (у х2) или ((у — + х2 25);
З) (у > х2) или ((у — + х2 25);
4) (у > х2) и ((у — + х2 25);
5) другое условие, нежели указанные.
В1. Перечислите номера тех пунктов, в которых указаны цели, достижимые при компьютерном моделировании облика и поведения динозавров, а также среды их обитания. В ответе расположите номера в порядке возрастания без пробелов и знаков препинания (например, 124).
1) Проверка гипотез о причинах гибели динозавров.
2) Повышение уровня безопасности исследователей.
З) Изучение возможности клонирования динозавров в современных условиях.
4) Понижение стоимости исследований.
В2*. В город лт с дружеским визитом прибыл инопланетянин. Во время торжественной встречи выяснилось, что он постоянно меняет форму, превращаясь то в шар, то в треугольную пирамиду, то в цилиндр. Если в некоторый момент времени инопланетянин имеет некоторую форму, то ровно через секунду он случайным образом меняет её на одну из двух других своих форм. При этом оказалось, что, хотя переход в новую форму каждый раз происходит случайно, при выборе из двух форм форму шара инопланетянин принимает в два раза чаще, а между пирамидой и цилиндром предпочтений не наблюдается. Для компьютерного моделирования этого процесса был составлен алгоритм, который по введённому времени t сообщает, какую форму в этот момент примет инопланетянин. Какой из приведённых ниже алгоритмов адекватно отражает процесс превращения инопланетянина, если в начальный момент он имел форму шара? В ответе перечислите через запятую номера правильных, по вашему мнению, алгоритмов; если правильного алгоритма нет, то в ответе запишите число О.
1) Алгоритм
Форма_инопланетянина цел: i, t; вещ: х; сим: s; { Запросить
t; ![]() ”Шар”;
”Шар”;
Делать Q.r i :![]()
{ Если (s — ”Шар”) то ![]() х дсч(2)•,
х дсч(2)•,
Если (х 1) то { :— ”Пирамида”; ![]() иначе { s ”Цилиндр”; }
иначе { s ”Цилиндр”; }
Есдц (8 —
”Цилиндр”) ![]()
![]() х дсч(3);
х дсч(3);
Если (х < 1) :— ”Пирамида”; ![]() иначе { s . ”Шар”;
иначе { s . ”Шар”; ![]()
Если (s = ”Пирамида”) то ![]() х дсч(3);
х дсч(3);
Если (х < 1) то { s ”Цилиндр”; } иначе
{ s • ”Шар”•, ![]()
Сообщить з;
2) Алгоритм Форма_инопланетянина цел: i, t; вещ: х; сим: s; { Запросить t;
![]() ”Шар"•,
”Шар"•,
![]() О;
О;
Делать пока (i t)
{ Если (s — ”Шар”) то ![]() х дсч(2);
х дсч(2);
Если (х < 1) то { s ”Пирамида”; ![]() иначе { s ”Цилиндр”; }
иначе { s ”Цилиндр”; }
Еед.ц (8 = ”Цилиндр”) то ![]() х дсч(3);
х дсч(3);
Если (х 1) то { s :— ”Пирамида”; } иначе
{ s . ”Шар”; ![]()
![]()
Если (8 — ”Пирамида”) r.Q ![]() х ДСЧ(3)•,
х ДСЧ(3)•,
Если (х < 1) то { s := ”Цилиндр”; ![]() иначе { s . ”Шар”;
иначе { s . ”Шар”; ![]()
![]()
Сообщить s;
З) Алгоритм Форма_инопланетянина цел: i, t; вещ: х; сим: з; { Запросить t;
![]() ”Шар";
”Шар";
Делать (i < t)
{ Если (s — ”Шар”) И (i < t) то х дсч(2)•,
Если (х t) !..Q { s ”Пирамида”; ![]()
ИУДУ.е s ”Цилиндр”; ![]()
Если (8 — ”Цилиндр”) И (i t) то
{ х ДСЧ(3)•,
Если (х < 1) r.Q : ”Пирамида”; ![]() ица.уе { s ”Шар”;
ица.уе { s ”Шар”; ![]()
Если (s — ”Пирамида”) И (i t) то![]()
{ х дсч(3);
Если (х < 1) { s ”Цилиндр”; } иначе
{ 8 •.- ”Шар”•, ![]()
![]()
Сообщить з;
4) ![]() Форма_инопланетянина цед: i, t; вещ:
х; сим: s; { Запросить t;
Форма_инопланетянина цед: i, t; вещ:
х; сим: s; { Запросить t;
![]()
Делать от i е.— 1![]()
{ Если
(s = ”Шар”) r.Q ![]() х дсч(2);
х дсч(2);
Если (х 1) то { s :— ”Пирамида”; ![]()
ИИ..У2 { 8 ”Цилиндр”; }
иначе
{ Если
(8 — ”Цилиндр”) r.Q ![]() х ДСЧ(3)•,
х ДСЧ(3)•,
Е.ед.и (х 1) то { s ”Пирамида”; } иначе { s ”Шар”; }
ин ч
{ Е.ед.и (8 =
”Пирамида”) r.Q х ДСЧ(3)•, Если (х < 2) { :![]()
иначе { s . — ”Цилиндр”; ![]()
![]()
Сообщить з;
5) Алгоритм Форма_инопланетянина цед: i, t; вещ: х; сим: з; { Запросить t;
![]() ”Шар”•,
”Шар”•,
Делать от i 1![]()
{ Ерли (s — ”Шар”) то
{ х дсч(3);
Если (х < 1) то { s . — ”Пирамида”; ![]()
ИМ.а.У.е { s ”Цилиндр”; ![]()
ицауе
{ Если (8 = ”Цилиндр”) то
{ х дсч(2);
Если (х < 1) {s . ”Пирамида”; } иначе
{ ”Шар”; ![]()
ин ч
{ Если (8 = ”Пирамида”) то
{ х дсч(2)•,
Ерли (х 1) то { s ”Цилиндр”; } ицауе { ”Шар”•,
![]()
Сообщить s;
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
А1 |
|
|
|
|
|
|
|
|
Тест 8
Алгебра логики
Вариант 1
Ниже приняты следующие обозначения логических операций над переменными:
а) — (например, —А) отрицание (инверсия, логическое НЕ);
б) Л (например, А Л В) — конъюнкция (логическое умножение, логическое И);
в) V (например, А В) дизъюнкция (логическое сложение, логическое ИЛИ);
г) (например, А В) — следование (импликация).
![]() Приоритеты логических операций таковы: инверсия
(отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое
сложение), следование (импликация). Таким образом, —А л В С л D совпадает с
((—А) л В)
Приоритеты логических операций таковы: инверсия
(отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое
сложение), следование (импликация). Таким образом, —А л В С л D совпадает с
((—А) л В) ![]()
![]() (С л D). Возможна запись А л В л С вместо
(Ал В) л С. То же относится и к дизъюнкции: возможна запись А м В м С вместо (А
V В) С.
(С л D). Возможна запись А л В л С вместо
(Ал В) л С. То же относится и к дизъюнкции: возможна запись А м В м С вместо (А
V В) С.
А1. Какая из логических операций не будет иметь истинного значения, когда все аргументы истинны?
1) импликация; 2) дизъюнкция; З) конъюнкция; 4) исключающее ИЛИ; 5) никакая из указанных операций.
А2. Укажите, какое логическое выражение равносильно выражению — (—А v —В л С):
![]()
2) -AvBv -С;
3) А м ВМС;
4)
Ал (В М![]()
5) ни одно из приведённых выражений.
АЗ. Какая из таблиц истинности соответствует формуле
![]() у) = —(xvy) Л
у) = —(xvy) Л![]()
1)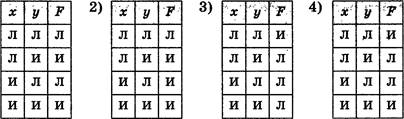
5) ни одна из приведённых таблиц
В1. Среди записанных ниже предложений выберите высказывания и запишите через запятую их номера в порядке возрастания.
1) Земля имеет форму шара.
2) Найдите остаток при делении числа 9 на 7.
З) В десятичной записи числа 1/29 встречается 7 раз подряд цифра 7.
4) Окружность вписана в треугольник.
5) Верно ли, что в любом треугольнике полупериметр больше любой из его сторон?
6) Существует чётное число, делящееся нацело на З.
В2. Известно, что высказывание
![]()
истинно. Какое наименьшее число ложных высказываний может быть среди высказываний А, В и С?
ВЗ. Следующее логическое выражение рассматривается при целых значениях переменных х и у:
— (у2 — х2 16) 'V (( х нацело делится на у) Л з З
![]()
Запишите через запятую в порядке возрастания номера тех пар значений переменных, для которых данное выражение истинно:
![]()
![]()
![]() 4) х - 2007, у - 9;
4) х - 2007, у - 9;
В4. Три друга — Алёша, Боря и Витя — учатся в одном классе. Один ездит домой из школы на автобусе, другой на метро, третий на троллейбусе. Однажды после уроков Витя пошёл проводить своего друга до станции метро. Когда мимо них проезжал троллейбус, из его окна третий друг крикнул: «Боря, ты забыл в школе тетрадку!» Определите, кто едет на автобусе, кто на метро, а кто на троллейбусе. Ответ запишите в виде последовательности, состоящей из первых букв имён мальчиков, в том порядке, в котором перечислены виды транспорта.
В5. В спортивный лагерь приехали 4 школьника: Петя, Лёня, Коля и Андрей. Каждый из них занимается ровно одним из видов спорта: баскетболом, футболом, волейболом или бадминтоном. Руководитель лагеря спросил, каким именно видом спорта занимается каждый из них. Коля сказал, что Петя увлекается волейболом, а Лёня — бадминтоном. Андрей ответил, что, насколько он знает, Лёня играет в баскетбол, а Коля в бадминтон. Позже выяснилось, что в каждом ответе только одно утверждение истинно. Можно ли на основании этой информации сделать вывод, что Андрей не играет в футбол?
Запишите в ответ букву «в», если такой вывод сделать можно, букву «ф», если можно сделать вывод, что Андрей играет в футбол, и букву «н», если информации недостаточно, чтобы сделать определённый вывод.
Вб. Цифрами обозначены непересекающиеся области, на которые разбиваются круг, треугольник и прямоугольник при указанном на рисунке взаимном расположении этих фигур.
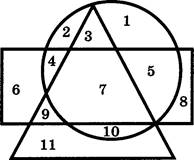
Пусть через А обозначено высказывание «Точка принадлежит кругу», через В — высказывание «Точка принадлежит треугольнику», через С высказывание «Точка принадлежит прямоугольнику». Напишите через запятую в порядке возрастания номера тех областей, для которых будет истинным выражение
в л -С У С л (А— В)
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

|
вз |
|
|
Вб |
|
|
|
|
|
Тест 8
Алгебра логики
Вариант 2
Ниже приняты следующие обозначения логических операций над переменными:
а) — (например, —А) отрицание (инверсия, логическое НЕ);
б) Л (например, А Л В) — КОНЪЮНКЦИЯ (логическое умножение, логическое И);
в) V (например, А 'V В) Дизъюнкция (логическое сложение, логическое ИЛИ);
г) (например, А В) — следование (импликация).
Приоритеты логических операций таковы: отрицание (инверсия), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), следование (импликация). Таким образом, — А л В С л D совпадает с ((—А) л В) м (С л Т. Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции: возможна запись AVBVC вместо (AVB)VC.
А1. Какая из логических операций будет давать истинное значение, когда все аргументы ложны? 1) конъюнкция; 2) дизъюнкция; З) импликация; 4) исключающее ИЛИ; 5) никакая из указанных операций.
А2. Укажите, какое логическое выражение равносильно выражению — (—А л —В С):
![]()
2) -AvBv-C;
![]()
5) ни одно из приведённых выражений.
8—Гейн. Тесты. 10 кл.
АЗ. Какая из таблиц истинности соответствует формуле
![]()
1)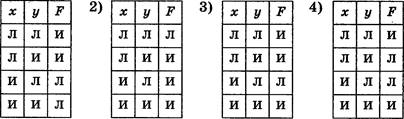
5) ни одна из приведённых таблиц
В1. Среди записанных ниже предложений выберите высказывания и запишите через запятую их номера в порядке возрастания.
1) Предложение, которое вы читаете, не является истинным высказыванием.
2) В десятичной записи числа цифра 7 встречается не более 1000 раз.
З) Трапецию можно вписать в окружность.
4) Лёд легче воды.
5) Каждое число, заканчивающееся на цифру З, простое. 6) Делится ли число 102 753 на 37 без остатка?
В2. Известно, что высказывание
(Ал В) ев л -Ал С) (-С л -А)
ложно. Какое наименьшее число истинных высказываний может быть среди высказываний А, В и С?
ВЗ. Следующее логическое выражение рассматривается при целых значениях переменных х и у:
(у2 — х2 < 16) л ((у нацело делится на х) 'V
з З
![]()
Запишите через запятую в порядке возрастания номера тех пар значений переменных, для которых данное выражение истинно:
![]()
![]()
![]() 4) х - 9, у - 123;
4) х - 9, у - 123;
1 14
В4. Витя, Коля, Павел и Сергей учатся в 5, 6, 7 и 8 классах. В воскресенье они отправились в лес за грибами. Шестикласснику не повезло, он не нашёл ни одного гриба, а Павел нашёл 10 грибов. Витя и семиклассник нашли ежа и позвали Колю посмотреть на ежа. Восьмиклассник, шестиклассник и Коля объясняли Серёже, как ориентироваться на местности. Определите, в каком классе учится каждый из мальчиков. Ответ запишите в виде последовательности, состоящей из первых букв имён мальчиков, в порядке возрастания номеров классов, в которых они учатся.
В5. Ребята решили поздравить четырёх девушек ![]() Машу, Дашу,
Олю и Галю — с праздником 8 Марта и купить каждой по цветку. Они спросили
девушек, какие цветы им нравятся, зная, что каждая из них любит такие цветы,
которые не нравятся трём другим. Две девушки ответили так. Галя сказала, что
Оля любит тюльпаны, а Даша — розы. Оля же сказала, что Даша любит хризантемы, а
Маша любит лилии. Слышавшая это Маша сказала ребятам по секрету, что обе
девушки лукавят в каждом ответе только половина истинна, хотя любимые цветы
девушек перечислены правильно. Можно ли, считая, что Маша говорит чистую
правду, сделать вывод, что ей нравятся тюльпаны?
Машу, Дашу,
Олю и Галю — с праздником 8 Марта и купить каждой по цветку. Они спросили
девушек, какие цветы им нравятся, зная, что каждая из них любит такие цветы,
которые не нравятся трём другим. Две девушки ответили так. Галя сказала, что
Оля любит тюльпаны, а Даша — розы. Оля же сказала, что Даша любит хризантемы, а
Маша любит лилии. Слышавшая это Маша сказала ребятам по секрету, что обе
девушки лукавят в каждом ответе только половина истинна, хотя любимые цветы
девушек перечислены правильно. Можно ли, считая, что Маша говорит чистую
правду, сделать вывод, что ей нравятся тюльпаны?
Запишите в ответ букву «в», если такой вывод сделать можно, букву «д», если можно сделать вывод, что Маше нравятся другие цветы, и букву «н», если информации недостаточно, чтобы определённо утверждать, любит Маша тюльпаны или нет.
Вб. Цифрами обозначены непересекающиеся области, на которые разбиваются круг, треугольник и прямоугольник при указанном на рисунке взаимном расположении этих фигур.
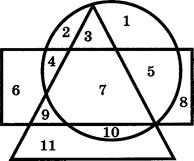
Пусть через А обозначено высказывание «Точка принадлежит кругу», через В — высказывание «Точка принадлежит треугольнику», через С высказывание «Точка принадлежит прямоугольнику». Напишите через запятую в порядке возрастания номера тех областей, для которых будет истинным выражение
![]()
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()


Тест 8
Алгебра логики
Вариант З
Ниже приняты следующие обозначения логических операций над переменными:
а) (например, —А) отрицание (инверсия, логическое НЕ);
б) Л (например, А Л В) — КОНЪЮНКЦИЯ (логическое умножение, логическое И);
в) (например, А V В) ДИЗЪЮНКЦИЯ (логическое сложение, логическое ИЛИ);
г) (например, А В) — следование (импликация).
Приоритеты логических операций таковы: отрицание (инверсия),
конъюнкция (логическое умножение), дизъюнкция (логическое сложение), следование
(импликация). Таким образом, — АЛВ v С совпадает с ((—А) л В) V ![]() (С л D).
Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции:
возможна запись А В V С вместо (А В) С.
(С л D).
Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции:
возможна запись А В V С вместо (А В) С.
![]() А1. Какая из логических операций будет
иметь истинное значение, когда первый аргумент истинен, а второй ложен?
А1. Какая из логических операций будет
иметь истинное значение, когда первый аргумент истинен, а второй ложен?
1) конъюнкция; 2) дизъюнкция; З) импликация; 4) равносильность; 5) никакая из указанных операций.
А2. Укажите, какое логическое выражение равносильно выражению — (—А л — В 'v С):
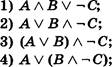
5) ни одно из приведённых выражений.
АЗ. Какая из таблиц истинности соответствует формуле
![]()
1)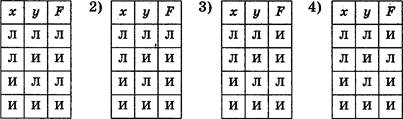
5) ни одна из приведённых таблиц
В1. Среди записанных ниже предложений выберите высказывания и запишите через запятую их номера в порядке возрастания.
1) Никогда не говори «никогда».
2) Можно ли утверждать, что любой четырёхугольник, у которого все углы равны, является прямоугольником?
З) Это предложение не является высказыванием.
4) Чётное число делится нацело на З.
5) Между любыми двумя рациональными числами найдётся хотя бы одно иррациональное число.
6) А. С. Пушкин — великий поэт XIX века.
В2. Известно, что высказывание
(-Av В) лев мА С) л (-с м -А)
истинно. Какое наименьшее число ложных высказываний может быть среди высказываний А, В и С?
ВЗ. Следующее логическое выражение рассматривается при целых значениях переменных х и у:
(—( у2 — х2 16)
л (у нацело делится на х)) х./ ![]() з з
з з
Запишите через запятую в порядке возрастания номера тех пар значений переменных, для которых данное выражение истинно:

В4. Алёша, Боря, Витя и Гриша сидят за круглым столом. Один из них — лыжник, другой — конькобежец, третий — фигурист, четвёртый — биатлонист. Алёша не катается на коньках, лыжник сидит между Борей и биатлонистом, Витя сидит между Гришей и фигуристом. Определите, кто каким видом спорта занимается. Ответ запишите в виде последовательности, состоящей из первых букв имён спортсменов, в следующем порядке перечисления видов спорта, которыми они занимаются: биатлон, конькобежный спорт, лыжи, фигурное катание.
В5. На первом туре школьной математической олимпиады было предложено 4 задачи. После проверки участникам стало известно, что лидеры — Вася, Коля, Петя и Марина — решили по З задачи, причём каждая из предлагавшикся задач хотя бы одному из них оказалась не по зубам. Вася и Коля, обсуждая ситуацию, высказали такие утверждения. Коля: «Я уверен, что правильно решил вторую, третью и четвёртую задачи, а вот Петя со второй задачей не справился». На это Вася возразил, что вторую задачу наверняка не решила Марина, а он не уверен в правильности своего решения четвёртой задачи. Проходивший мимо член жюри заметил, что в каждом из высказываний ребят одно утверждение истинно, а другое ложно. Можно ли сделать вывод, что третью задачу правильно решили и Петя, и Марина?
Запишите в ответ букву «в», если такой вывод сделать можно, букву «л», если можно сделать вывод, что высказанное утверждение неверно, и букву «н», если информации недостаточно, чтобы определённо утверждать, истинно или ложно данное утверждение.
Вб. Цифрами обозначены непересекающиеся области, на которые разбиваются круг, треугольник и прямоугольник при указанном на рисунке взаимном расположении этих фигур.
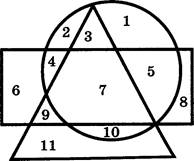
Пусть через А обозначено высказывание «Точка принадлежит кругу», через В — высказывание «Точка принадлежит треугольнику», через С — высказывание «Точка принадлежит прямоугольнику». Напишите через запятую в порядке возрастания номера тех областей, для которых будет истинным выражение
- Ал -вл С л (С— В)
Бланк
ответов ![]()
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
АЗ |
|
|
|
||||
|
|
|
|
|
|
|
||||
|
вз |
|
|
|
|||||
|
|
|
|
|
|||||
Тест 8
Алгебра логики
Вариант 4
Ниже приняты следующие обозначения логических операций над переменными:
а) — (например, — А) отрицание (инверсия, логическое НЕ);
б) Л (например, А Л В) — конъюнкция (логическое умножение, логическое И);
в) х../ (например, А V В) дизъюнкция (логическое сложение, логическое ИЛИ);
г) (например, А В) — следование (импликация).
Приоритеты логических операций таковы: отрицание (инверсия),
конъюнкция (логическое умножение), дизъюнкция (логическое сложение), следование
(импликация). Таким образом, —А л В С л D совпадает с ((—А) л В) ![]() (С л D).
Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции:
возможна запись А V В V х./ С вместо (А V В) х./ С.
(С л D).
Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции:
возможна запись А V В V х./ С вместо (А V В) х./ С.
А 1. Какая из логических операций будет всегда давать истинное значение, когда хотя бы один из двух аргументов ложен?
1) конъюнкция; 2) дизъюнкция; З) импликация; 4) исключающее ИЛИ; 5) никакая из указанных операций.
А2. Укажите, какое логическое выражение равносильно выражению — (—А л В —С):
![]()
3) Ал-ВлС;
4) -Av -Bvc•,
5) ни одно из приведённых выражений.
АЗ. Какая из таблиц истинности соответствует формуле
![]() —(хлу)лх — х ?
—(хлу)лх — х ?
1)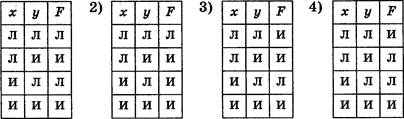
5) ни одна из приведённых таблиц
В1. Среди записанных ниже предложений выберите высказывания и запишите через запятую их номера в порядке возрастания.
1) Солнце — источник жизни на Земле.
2) Чётное число при делении на З даёт в остатке чётное число.
З) Спой, светик, не стыдись.
4) Нет в жизни счастья.
5) Неизвестно, сколько раз цифра О встречается в десятичной записи числа п.
6) Среди перечисленных предложений нет высказываний.
В2. Известно, что высказывание
![]()
ложно. Какое наименьшее число истинных высказываний может быть среди высказываний А, В и С?
ВЗ. Следующее логическое выражение рассматривается при целых значениях переменных х и у:
![]() у2 — х2
у2 — х2 ![]() 16)
V (х нацело делится на у)) Л
16)
V (х нацело делится на у)) Л
Л —(х + уз < < хз + У)•
Запишите через запятую в порядке возрастания номера тех пар значений переменных, для которых данное выражение истинно:
![]()
![]()
![]() 4) х - 1000, у - 8;
4) х - 1000, у - 8;
В4. Четыре юниора — Алёша, Боря, Витя и Гриша приехали в летний спортивный лагерь. Один из них — пловец, другой — бегун, третий — велосипедист, а четвёртый занимается прыжками в воду с трамплина. Чтобы познакомиться, они сели на скамейку и разговорились. Оказалось, что Витя сидит между бегуном и пловцом, а бегун в свою очередь сидит между Гришей и велосипедистом. Боря оказался единственным среди них, кто не умеет плавать. Определите, кто каким видом спорта занимается. Ответ запишите в виде последовательности, состоящей из первых букв имён юношей, в следующем порядке перечисления видов спорта, которыми они занимаются: бег, велосипедный спорт, плавание, прыжки с трамплина.
Вб. На занятии литературного кружка учитель его участникам
предложил прочитать четыре разных стихотворения, одно из которых было написано
в XVII веке, другое — в XVIII, третье — в XIX и четвёртое совсем недавно в ХХ
веке. Затем он спросил, могут ли участники кружка по стилю произведения
определить, в каком веке было написано каждое из стихотворений. Коля
предположил, что первое из предложенных стихотворений написано в ХИХ веке, а
третье ![]() в XVIII. Лена возразила, что третье
стихотворение написано, конечно, в ХХ веке, а вот четвёртое, вероятнее всего, в
XVII. Учитель сказал, что в каждом из высказываний ребят одно утверждение
истинно, а другое ложно. Можно ли сделать вывод, что второе из предложенных
стихотворений было написано либо в XIX, либо в ХХ веке?
в XVIII. Лена возразила, что третье
стихотворение написано, конечно, в ХХ веке, а вот четвёртое, вероятнее всего, в
XVII. Учитель сказал, что в каждом из высказываний ребят одно утверждение
истинно, а другое ложно. Можно ли сделать вывод, что второе из предложенных
стихотворений было написано либо в XIX, либо в ХХ веке?
Запишите в ответ букву «в», если такой вывод сделать можно, букву «л», если можно сделать вывод, что высказанное утверждение неверно, и букву «н», если информации недостаточно, чтобы определённо утверждать, истинно или ложно данное утверждение.
Вб. Цифрами обозначены непересекающиеся области, на которые разбиваются круг, треугольник и прямоугольник при указанном на рисунке взаимном расположении этих фигур.
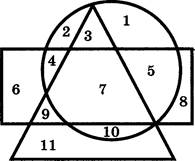
Пусть через А обозначено высказывание «Точка принадлежит кругу», через В — высказывание «Точка принадлежит треугольнику», через С высказывание «Точка принадлежит прямоугольнику». Напишите через запятую в порядке возрастания номера тех областей, для которых будет истинным выражение
![]()
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

|
вз |
|
|
Вб |
|
|
|
|
|
Тест 9
Базы данных
Вариант 1.
Ниже приведены фрагменты двух таблиц базы данных «Школьная библиотека». Первая таблица — это каталог книг (в сокращённом виде), вторая выступает в роли журнала выдачи книг из библиотеки. Выполняя задания данного теста, используйте информацию, представленную в этих таблицах.
|
Таблица |
|
|
|
|
|
1 |
Васина И. К. |
У реки |
2000 |
Повесть |
|
2 |
Венцев Т.П. |
Фонтаны |
1996 |
Фотоальбом |
|
З |
Дикин И. С. |
Былое |
1998 |
Мемуары |
|
4 |
Дикин И. С. |
Былое |
2000 |
Мемуары |
|
5 |
Дремов С. Н. |
Не зная прошлого |
1999 |
Роман |
|
6 |
Жданов О. В. |
Воспоминания |
2001 |
Мемуары |
|
7 |
Жданов О. В. |
Шаги в тишине |
1998 |
Детектив |
|
8 |
Иткин Д. Ш. |
Ничего не боясь |
1999 |
Роман |
|
9 |
Крутов И. В. |
Дорогой борьбы |
2002 |
Повесть |
|
10 |
Николаев А. М. |
Яблоневый цвет |
2001 |
Стихи |
|
11 |
Петров А. И. |
Когда позовут... |
1998 |
Детектив |
|
12 |
|
|
|
|
таблица 2![]()
|
|
|
|
|
Дата выдачи |
Дата возвра |
|
1 |
Венцев Т.П. |
Фонтаны |
Колин П. |
08.04 |
22.04 |
|
2 |
Васина И. К. |
У реки |
Силин Д. |
10.04 |
17.04 |
|
З |
Дикин И. С. |
Былое |
Басов А. |
10.04 |
16.04 |
|
4 |
Жданов О. В. |
Шаги в тишине |
Носова Т. |
10.04 |
21.04 |
|
5 |
Макаров Б. В. |
Моё оружие |
Котова С. |
14.04 |
20.04 |
|
б |
Дикин И. С. |
Былое |
Егорова А. |
15.04 |
29.04 |
|
7 |
Жданов О.В. |
Воспоминания |
Антонов Б. |
17.04 |
30.04 |
|
8 |
Иткин Д.Ш. |
Ничего не боясь |
Уколов Н. |
17.04 |
22.04 |
|
9 |
Васина ИЖ. |
У реки |
Носова Т. |
20.04 |
01.05 |
|
10 |
Дремов С.Н. |
Не зная прошлого |
Юдин Р. |
22.04 |
05.05 |
|
11 |
Николаев ХМ. |
Яблоневый цвет |
Колин П. |
22.04 |
29.04 |
|
12 |
Петров ХИ. |
Когда позовут.„ |
Сёмина А. |
24.04 |
11.05 |
|
13 |
|
|
|
|
|
М. Какие номера из видимой части таблицы 2 имеют записи, удовлетворяющие запросу
Дата возврата > 20.04 и Дата возврата < 01.О5?
![]()
2)
1, 4, 6, 7, 9, 11![]()
3)
1, 4, 6, 7, 8, 11![]()
4) с 4-й по 8-ю;
5) все, кроме 2, з, 10 и 12.
А2. В таблице 2 проведена сортировка первых двенадцати строк по полю Кому рыдано в алфавитном порядке, а затем для одинаковых значений в этом поле по убыванию поля Дата возврата. После этого номера строк расположились в следующем порядке:
1) 7, з, 6, 11, 1, 5, 9, 4, 12, 2, 8, 10;
2) 7, з, 6, 11, 1, 5, 4, 9, 8, 12, 2, 10;
3) 7, з, 6, 1, 11, 5, 4, 9, 12, 2, 8, 10;
4) 7, з, 6, 11, 1, 9, 4, 5, 8, 12, 2, 10;
5) в ином порядке, нежели это указано в пунктах 1—4.
АЗ. Запрос, позволяющий получить фамилии тех, кто брал в мае романы или повести, можно записать так:
1) Жанр = ”Роман" или Жанр = ”Повесть" ш и Дата выдачи > 01.05 ш дата выдачи < 31.05 2) Жанр = ”РоманП или Жанр = “Повесть" и и Дата выдачи > 30.04 и Дата выдачи < 01.06 З) (Жанр = Томан“ или Жанр = “Повесть“) и и (Дата выдачи > 01.О5 и дата выдачи < 31.О5) 4) (Жанр = Томан“ или Жанр = “Повесть“) и и Дата выдачи > 30.04 и Дата выдачи < 01.06
5) ни одна из указанных формул запроса не годится
М. Согласно запросу
Год издания < 2000 была сформирована таблица-результат со следующими атрибутами (полями):
|
|
Кому выдана |
В ней оказалось 8 записей, и они были отсортированы в алфавитном порядке фамилий авторов. В первой записи указанным оказался читатель по фамилии:
1) Носова; 2) Колин;
З) Егорова; 4) Антонов;
5) по представленной информации нельзя указать фамилию читателя.
В1. Сколько текстовых полей в той части таблицы 2, которая представлена в начале теста?
В2*. Между таблицами 1 и 2 было установлено соединение по полям Автор и Название. Укажите номер, • под которым указан правильный тип соединения; если соединение по этим полям установить нельзя, то запишите в ответе О.
1) один к одному; 2) один ко многим;
З) многие к одному; 4) многие ко многим.
ВЗ*. Анализ спроса литературы показал, что с 1 по
|
|
Количество |
|
дата выдачи < 15.04 и Жанр <> “Повесть” |
107 |
|
Жанр = “Повесть" или Жанр = ИРоман” |
158 |
|
дата выдачи 15.04 и Модель <> ”РоманП |
134 |
30 апреля было ровно 287 читателей, каждый из которых взял в библиотеке ровно одну книгу. В следующей таблице приведено количество записей, полученных с использованием рассматриваемой базы данных на некоторые запросы об этом контингенте читателей.
Найдите количество записей, удовлетворяющих запросу:
Дата выдачи < 05.04 и Жанр = Томан“ или иди Дата выдачи > = 15.04 и Жанр = “Повесть".
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
АЗ |
|
|
|
|
|
|
|
|
|
|
Тест 9
Базы данных Вариант 2
Ниже приведены фрагменты двух таблиц из базы данных «Телефонная компания». Первая таблица содержит информацию об абонентах (в сокращённом виде), вторая выступает в роли журнала регистрации звонков (в течение одного часа). Выполняя задания данного теста, используйте информацию, представленную в этих таблицах.
|
Таблица 1 |
|
||||
|
|
|
|
Дата подключения |
|
|
|
1 |
Васина И. К. |
9222475815 |
12.07.08 |
Бизнес |
|
|
2 |
котов АЛ. |
9062451238 |
12.01.09 |
Близкий |
|
|
з |
Крутов И. В. |
9043571245 |
30.03.08 |
Эконом |
|
|
4 |
Крутов И. В. |
9041245045 |
21.12.08 |
Близкий |
|
|
5 |
Оглоблин Ф.Р. |
9064215544 |
07.06.09 |
Бизнес |
|
|
б |
Петров А.И. |
9182546284 |
13.06.08 |
Полный |
|
|
7 |
Петров ХИ. |
9184257436 |
31.01.09 |
Эконом |
|
|
8 |
Сидорова О.С. |
9222414578 |
25.06.08 |
Эконом |
|
|
9 |
Сотов А.В. |
9222145721 |
26.11.08 |
Бизнес |
|
|
10 |
|
|
|
|
|
9—Гейн. 10 кл.
|
Таблица 2 |
|
||||
|
|
Номер телефона |
Время разговора |
Продолжительность разговора |
Стоимость усдуги, |
|
|
1 |
9043571245 |
13:02:54 |
0:54 |
1,35 |
|
|
2 |
9182546284 |
13:05:12 |
1:28 |
2,20 |
|
|
з |
9062451238 |
|
0:37 |
0,93 |
|
|
4 |
9222145721 |
13:07:28 |
3:46 |
5,65 |
|
|
5 |
9064215544 |
13:08:58 |
2:09 |
3,48 |
|
|
6 |
9182546284 |
13:10:11 |
0:57 |
1,40 |
|
|
7 |
9041245045 |
13:10:45 |
5:48 |
8,63 |
|
|
8 |
9222414578 |
13:10:50 |
1:27 |
2,18 |
|
|
9 |
9184257436 |
|
2:09 |
3,35 |
|
|
10 |
9222414578 |
|
7:13 |
10,83 |
|
|
11 |
9222475815 |
|
0:37 |
0,80 |
|
|
12 |
9182546284 |
|
0:59 |
1,48 |
|
|
13 |
|
|
|
|
|
А1. Какие номера из видимой части таблицы 1 имеют записи, удовлетворяющие запросу
Дата подключения > 30.05.08 и Дата подключения < 31.01.О9?
![]() З)
все, кроме З и 5;
З)
все, кроме З и 5; ![]()
5) таких записей нет.
А2. В таблице 2 проведена сортировка по возрастанию первых двенадцати строк по полю Продолжительность разговора, а затем для одинаковых значений в этом поле по убыванию поля Стоимость услуги. После этого номера строк расположились в следующем порядке:
1)
11, з, 1, 6, 12,
8, 2, 9, 5, 4, 7 10![]()
2)
з, 11, 1, 6, 12,
8, 2, 5, 9, 4, 7 10![]()
3)
10, 7, 4, 5, 9,
2, 8, 12, 6, 1, з 11![]()
4)
10, 7, 4, 9, 5,
2, 8, 12, 6, 1, 11 з![]()
5) в ином порядке, нежели это указано в пунктах 1—4.
АЗ. Запрос, позволяющий получить фамилии владельцев тех телефонов, которые звонили после 13:00 по тарифному плану «Бизнес» или «Эконом», можно записать так:
1) Время звонка > 13:00 и Тариф = “Бизнес" иди иди Тариф = ”Эконом"
2) Время звонка > 13:00 и Тариф = ”Бизнес” или или Тариф = Юконом“
З) Время звонка > 13:00 и Тариф = ”БизнесП или шли Тариф = «Эконом“)
4) (Время звонка > 13:00 и Тариф = “Бизнес") или или Тариф = ”ЭкономП
5) ни одна из указанных формул запроса не годится
М. Согласно запросу
Продолжительность разговора > 2:00
была сформирована таблица-результат со следующими атк рибутами (полями):
![]()
В ней оказалось б записей, и они были отсортированы в алфавитном порядке фамилий владельцев. В первой записи стоимость услуги оказалась равна:
1) 10 р. 83 к.; 2) 8 р. 63 к.;
3) З р. 35 к.; 4) 80 к.;
5) по представленной информации нельзя определить стоимость услуги указанному владельцу.
В1. Сколько текстовых полей в той части таблицы 2, которая представлена в конце теста?
В2*. Между таблицами 1 и 2 было установлено соединение по полю Номер телефона. Укажите номер, под которым указан правильный тип соединения; если соединение по этим полям установить нельзя, то запишите в ответе О.
1) один к одному; 2) один ко многим;
З) многие к одному; 4) многие ко многим.
ВЗ*. В течение 12 апреля было зарегистрировано 1278 звонков. В следующей таблице приведено количество записей, полученных с использованием рассматриваемой базы данных на некоторые запросы.
Найдите количество записей, удовлетворяющих запросу:
|
Запрос |
Количество |
|
Продолжительность разговора < 2:00 и Тариф <> “Бизнес” |
742 |
|
Тариф — или |
912 |
|
Продолжительность разговора 2:00 и Тариф <> ”Эконом” |
437 |
Продолжительность разговора с: 2:00 и Тариф = (Эконом“ или или Продолжительность разговора >= 2:00 и и Тариф = ”Бизнес“.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()

Тест 9
Базы данных
Вариант 3
Ниже приведены фрагменты двух таблиц из базы данных «Кондитерская фабрика». Первая таблица содержит сведения о выпускаемой продукции (в представленном фрагменте только о тортах), вторая выступает в роли журнала поставок в три фирменных магазина фабрики. Выполняя задания данного теста, используйте информацию, представленную в этих таблицах.
Таблица 1
|
|
Наименование |
Основа
|
|
Весе кг |
Время выпуска |
Це |
|
|
||||||
|
1 |
Праздник |
Бисквит |
Сливочный |
1,2 |
9:00 |
268 |
|
2 |
Праздник |
Бисквит |
Сливочный |
0,6 |
9:00 |
145 |
|
З |
Москвичка |
Песочная |
Белковый |
0,7 |
8:00 |
164 |
|
4 |
Нежность |
Слоёная |
Йогуртовый |
0,65 |
8:00 |
170 |
|
5 |
Фантазия |
Бисквит |
Сметанный |
0,8 |
9:00 |
195 |
|
б |
Семь чудес |
Бисквит |
Белковый |
0,9 |
11:00 |
211 |
|
7 |
Семь чудес |
Бисквит |
Белковый |
0,45 |
11:00 |
115 |
|
8 |
Бархат |
Слоёная |
Сливочный |
0,95 |
10:00 |
230 |
|
9 |
Наполеон |
Слоёная |
Йогуртовый |
0,6 |
10:00 |
166 |
|
10 |
Праздник |
Бисквит |
Сливочный |
1,2 |
13:00 |
268 |
|
11 |
Праздник |
Бисквит |
Сливочный |
0,6 |
13:00 |
145 |
|
12 |
Москвичка |
Песочная |
Белковый |
0,7 |
15:00 |
164 |
|
13 |
Нежность |
Слоёная |
Йогуртовый |
0,65 |
15:00 |
170 |
|
14 |
|
|
|
|
|
|
Таблица 2
|
Д
|
Наименование , изделия |
|
Маг. ЛЬ 1,
|
|
2, |
|
З,
|
|
1 |
Праздник |
1,2 |
7 |
15 |
|
6 |
|
|
2 |
Праздник |
|
15 |
зо |
|
10 |
|
|
З |
Москвичка |
|
6 |
20 |
|
15 |
|
|
4 |
Нежность |
0,65 |
12 |
25 |
|
8 |
|
|
5 |
Фантазия |
0,8 |
15 |
15 |
|
10 |
|
|
б |
Семь чудес |
0,9 |
8 |
10 |
|
5 |
|
|
7 |
Семь чудес |
0,45 |
20 |
25 |
|
15 |
|
|
8 |
Бархат |
0,95 |
12 |
5 |
|
10 |
|
|
9 |
Наполеон |
0,6 |
15 |
18 |
|
10 |
|
|
10 |
|
|
|
|
|
||
А1. Какие номера из видимой части таблицы 1 имеют записи, удовлетворяющие запросу
Цена = 220 и вес 0,7?
1) з, 4, 5, 6, 12, 13; 2) все, кроме 1, 2, 10 и 11; 3) з, 5, 6, 12; 4) з, 4, 5, 6, 12; 5) таких записей нет.
А2. В таблице 1 проведена сортировка по убыванию первых тринадцати строк по полю Вес, а затем для одинаковых значений в этом поле по возрастанию поля Время выпуска. После этого номера строк расположились в следующем порядке:
1) 10, 1, 8, 6, 5, 12, з, 13, 4, 11, 9, 2, 7;
![]() 7, 11, 9, 2, 13, 4, 12, з, 5, 6, 8,
10, 1;
7, 11, 9, 2, 13, 4, 12, з, 5, 6, 8,
10, 1;
3) 7, 2, 9, 11, 4, 13, з, 12, 5, 6, 8, 1, 10;
4) 1, 10, 8, 6, 5, з, 12, 4, 13, 2, 9, 11, 7;
5) в ином порядке, нежели это указано в пунктах 1—4.
АЗ. Запрос, позволяющий получить наименования тех бисквитных и песочных тортов, которые были выпечены после 11:00, можно записать так:
1) Основа = ”Бисквит” или Основа = ”Песочная" и и Время выпуска > 11:00
2) Основа = ”Бисквит" и Основа = “Песочная" и ш Время выпуска > 11:00
З) Основа = ”Бисквит” или Основа = “Песочная П ) и и Время выпуска > 11:00
4) Основа = “Бисквит” и Основа = “Песочная“) или или Время выпуска > 11:00
5) ни одна из указанных формул запроса не годится.
М. Согласно запросу
Маг№1 > 10 иди Маг№2 > 15
была сформирована таблица-результат со следующими атрибутами (полями):
![]()
Эти записи были отсортированы в алфавитном порядке наименований. В последней записи оказался торт, цена которого:
1) 115 р.; 2) 166 р.; 3) 170 р.; 4) 211 р.; 5) 195 р.
В1. Сколько числовых полей в той части таблицы 1, которая представлена в начале теста?
В2*. Между таблицами 1 и 2 было установлено соединение по полям Наименование изделия и Вес. Укажите номер, под которым указан правильный тип соединения; если соединение по этим полям установить нельзя, то запишите в ответе О.
1) один к одному; 2) один ко многим;
З) многие к одному; 4) многие ко многим.
ВЗ*. В один из дней на кондитерской фабрике было изготовлено 185 тортов. В следующей таблице приведено количество записей, полученных с использованием рассматриваемой базы данных на некоторые запросы.
|
|
Количество |
|
Время выпуска 12:00 и Основа <> <>”Бисквит“ |
87 |
|
Основа <> «Песочная“ |
113 |
|
Время выпуска > 12:00 и Основа <> <>“Слоёная” |
56 |
Найдите количество записей, удовлетворяющих за-
![]() Время
выпуска = < 12:00 и Основа = Слоёная“ шли Время выпуска > 12:00 и Основа
= “Бисквит“ .
Время
выпуска = < 12:00 и Основа = Слоёная“ шли Время выпуска > 12:00 и Основа
= “Бисквит“ .
Бланк ответов
Фамилия, имя Класс
![]()
|
|
|
АЗ |
|
|
|
|
|
|
|
|
|
|
Тест 9
Базы данных
Вариант 4
|
Таблица 1 |
|||||
|
/п |
|
|
Номер автомобиля |
Код региона |
Дата регистрации |
|
1 |
Колесников А.П. |
Волга |
в1З7ао |
71 |
25.06.06 |
|
2 |
Петров ХИ. |
Хонда |
мб52ан |
66 |
31.12.06 |
|
З |
Крутов И. В. |
форд |
кЗ72оа |
77 |
15.02.05 |
|
4 |
Васина ИЖ. |
Хонда |
сЗ56рв |
77 |
13.03.05 |
|
5 |
Оглоблин Ф.Р. |
Жигули |
0258ав |
78 |
08.08.07 |
|
б |
Крутов И.В. |
Хонда |
с987км |
78 |
03.11.06 |
|
7 |
Сидорова О.С. |
Волга |
м45Знм |
77 |
12.12.07 |
|
8 |
Петров А.И. |
Жигули |
к 145вт |
66 |
25.01.05 |
|
9 |
|
|
|
|
|
![]() Ниже приведены фрагменты двух таблиц из базы данных
«Легковые автомобили». Первая таблица содержит сведения об автомобилях и их
владельцах, вторая используется для записи даты технического осмотра. Выполняя
задания М— АЗ и В1 данного теста, используйте информацию, представленную в этих
таблицах.
Ниже приведены фрагменты двух таблиц из базы данных
«Легковые автомобили». Первая таблица содержит сведения об автомобилях и их
владельцах, вторая используется для записи даты технического осмотра. Выполняя
задания М— АЗ и В1 данного теста, используйте информацию, представленную в этих
таблицах.
|
Таблица 2 * |
|
|
|
Номер автомобиля |
“Код региона |
Дата технического
|
|
к 145вт |
66 |
10.01.08 |
|
мб52ан |
66 |
21.03.08 |
|
с987км |
66 |
19.03.08 |
|
в1З7ао |
71 |
17.03.07 |
|
м45Знм |
77 |
29.12.07 |
|
н541сс |
77 |
13.03.08 |
|
р124на |
77 |
01.03.08 |
|
сЗ5брв |
77 |
29.02.08 |
|
0258ав |
78 |
11.11.07 |
|
с987км |
78 |
07.02.08 |
|
|
|
|
А1. Какие номера имеют записи из видимой части таблицы, удовлетворяющие запросу
Дата регистрации > 13.03.05 и и Дата регистрации < 09.09.07?
![]()
![]() 4) все, кроме З и 4;
4) все, кроме З и 4;
5) таких записей нет.
А2. При сортировке в порядке возрастания по полю Номер автомобиля первых восьми строк номера этих строк расположатся в следующем порядке:

5) в ином порядке, нежели это указано в пунктах 1 ![]() АЗ.
Запрос, позволяющий получить номера тех автомобилей марки «Волга» и «Жигули»,
которые были зарегистрированы не ранее 2006 г., можно записать так:
АЗ.
Запрос, позволяющий получить номера тех автомобилей марки «Волга» и «Жигули»,
которые были зарегистрированы не ранее 2006 г., можно записать так:
1) Модель = “Волга" и Модель = “Жигули П И и дата регистрации > 01.О1 .Об
2) Модель = “Волга“ и Модель = “Жигули" и и Дата регистрации 01.01.06
З) (Модель = “Волга“ иди Модель = “Жигули“) и и дата регистрации > 01.О1.О6
4) (Модель = “Волга" или Модель = ”Жигули") и и Дата регистрации >= 01.01 .Об
5) ни одна из указанных формул запроса не годится
М. Согласно запросу
Дата технического осмотра < 01.03.08
была сформирована таблица-результат со следующими атрибутами (полями):
![]()
В ней оказалось 6 записей, и они были отсортированы в алфавитном порядке фамилий владельцев. В первой записи оказалась следующая марка автомобиля:
1) Волга; • 2) Жигули; З) Форд; 4) Хонда;
5) по представленной информации нельзя указать марку автомобиля.
В1. Сколько текстовых полей в той части таблицы 1, которая представлена в начале теста?
В2*. Между таблицами 1 и 2 было установлено соединение по полям Номер автомобиля и Код региона. Укажите номер, под которым указан правильный тип соединения; если соединение по этим полям установить нельзя, то запишите в ответе О.
1) один к одному;
З) многие к одному;
2) один ко многим;
4) многие ко многим.
ВЗ*. В регионе с кодом 66 оказалось зарегистрировано 356 номеров с буквенным сочетанием «м...ан», а марки автомобилей, имеющих эти номера, таковы: «Хонда», «Волга» и «Жигули». Все автомобили прошли техосмотр в течение 2007 г. и 2008 г. В следующей таблице приведено количество записей, полученных с использованием рассматриваемой базы данных на некоторые запросы.
|
Запрос |
Количество |
|
дата технического осмотра < 01.01.08 и и Модель <> ”Жигули” |
187 |
|
Модель <> ”Волга” |
213 |
|
дата технического осмотра > 31.12.07 и и Модель <> ”Хонда” |
134 |
Найдите количество записей, удовлетворяющих запросу:
дата технического осмотра < 01.01.08 и и Модель — ”Хонда” или иди дата технического осмотра > 31.12.07 и и Модель — ”Жигули”.
Бланк ответов
Фамилия, имя ![]() Класс
Класс ![]()
|
|
|
АЗ |
|
|
|
|
|
|
|
|
|
|
![]() Ключи к тестовым заданиям
Ключи к тестовым заданиям
Тест 1
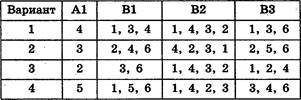
тест 2
|
Вариант |
А1 е |
М |
, АЗ |
|
|
вз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
256 |
56 |
1024 |
тест З
|
Вариант |
|
|
|
|
В2 |
вз |
м |
||||||
|
|
|
|
|
вквкввввввв |
324 |
|
|
||||||
|
|
|
|
|
ввввквввввв |
|
|
|
||||||
|
|
|
|
|
вввквв или вквквв |
142 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
Тест 4 |
|
||||||||||
|
Вариант |
А1 |
А2 |
В1 |
В2 |
ВЗ |
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
26 |
2,8 |
|
||||||
|
|
|
|
|
|
|
|
||||||
Тест 5
|
Вариант |
А1 |
А2 |
В1 |
В2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тест 6
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2п2 + 2 |
|
|
|
|
|
|
тест 7
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
234 |
|
|
|
|
|
|
|
![]()
В ответах для вариантов 1, З и 4 допустимы эквивалентные формулы, выражающие количество нулевых элементов массива в зависимости от чётности или нечётности числа п.
142
Тест 8
|
Вариант |
|
|
АЗ |
|
|
|
ВБА |
в |
|
|
|
|
|
|
|
|
квсп |
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
ГВАБ |
в |
|
|
|
|
|
|
|
|
БВАГ |
н |
тест 9
|
Вариант |
|
|
АЗ |
М |
В1 |
В2 |
ВЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учебное издание
Гейн Александр Георгиевич Юнерман Нина Ароновна
Информатика и ИКТ Тематические тесты
10 класс
Зав. редакцией Т. А. Бурмистрова Редактор О. В. Платонова
Художественный редактор О. П. Богомолова
Компьютерная графика С. А. Крутиков Техническое редактирование и компьютерная вёрстка Л. А. Ооржак, М. А. Носовой
Корректоры Л. А. Ермолина, И. Н. Панкова
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. изд. лиц. Серия ИД № 05824 от 12.09.01.
Подписано в печать 05.07.10. Формат ![]() Бумага газетная. Гарнитура
SchoolBookCSanPin. Печать офсетная. Уч.-изд. л. 5,92. Тираж 3000 экз. Заказ №
26361 (Щ-!щ).
Бумага газетная. Гарнитура
SchoolBookCSanPin. Печать офсетная. Уч.-изд. л. 5,92. Тираж 3000 экз. Заказ №
26361 (Щ-!щ).
Открытое акционерное общество «Издательство «Просвещение» . 127521, Москва, 3-й проезд Марьиной рощи, 41.
Открытое акционерное общество «Смоленский полиграфический комбинат». 214020, г. Смоленск, ул. Смольянинова, 1.
удк 373.167.1:004 ББК 32.81я72 Г29
Гейн А.Г.
Г29 Информатика и ИКТ. Тематические тесты. 10 класс / А. Г. Гейн, Н. А. Юнерман. — М. : Просвещение, 2010. 144 С. ил. ISBN 978-5-09019495-2.
Книга входит в учебно-методический комплект «Информатика и ИКТ» авторского коллектива под руководством А. Г. Гейна. Все задания даны в тестовой форме и в первую очередь предназначены для подготовки учащихся к сдаче экзаменов.
удк 373.167.1:004 ББК 32.81я72
ISBN 978-5-09-019495-2 С) Издательство «Просвещение», 2010 С) Художественное оформление.
Издательство «Просвещение», 2010
Все права защищены
ИНФОРМАТИКА и икт
ТЕМАТИЧЕСКИЕ ТЕСТЫ
Учебно-методический комплект по информатике и ИКТ включает:
А. Г. Гейн,
А. Б. Ливчак,
А. И. Сенокосов,
Н. А. Юнерман
Учебник для 10 класса
А. Г. Гейн
Книга для учителя Методические рекомендации к учебнику 10 класса
А. Г. гейн,
Н. А. Юнерман Тематические тесты для 10 класса
А. Г. гейн,
Н. А. Юнерман Задачник-практикум для 10—11 классов

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.