Поделиться
The first law of thermodynamics Statement game.pdf
PhysicsFactsheet 
April 2002 www.curriculumpress.co.uk Number 31
First Law of Thermodynamics
This Factsheet is about the first law of thermodynamics, which is concerned Specific latent heat
with how energy is transferred from and to any material. In order to If an object has a change in energy that results in a change of state, from solid understand the first law of thermodynamics we must first consider the to liquid, liquid to gas or vice versa, then the amount of mass changing from quantities used in expressing it. one state to another is governed by specific latent heat. Every material has
A Note of Caution two values of specific latent heat, one value for a change of state from a solid to a liquid, called the specific latent heat of fusion, and one value for a change
The sign convention for the terms in the first law of thermodynamics that have been used in this factsheet are consistent with AQA specification of state from a liquid into a gas, called the specific latent heat of vaporisation.
B and the Edexcel specifications. The AQA specification A unit 5 option
of applied physics defines work done on a gas as negative and the work If a substance is changing from a solid to a liquid or from a liquid to a gas then energy is being supplied to a substance and Q, is positive.
done by the gas as
positive. This means that the format of the first lawof thermodynamics takes
the form: ∆U
= Q- W. Please check that you If a substance is changing from a gas to a
liquid or a liquid to a solid then it are using the correct quantitative form
of the first law of thermodynamics with your specification. is losing energy
and the change in heat energy, Q, is negative.
|
Specific latent heat of fusion is the amount of energy required to turn 1 kg of a solid into a liquid. Specific latent heat of vaporisation is the amount of energy required to turn 1 kg of a liquid into a gas. Q l = specific latent heat are (Jkg-1) l = Q = heat energy supplied (J) m = mass of material changing state (kg) |
|
Q is a positive number when heat is supplied to an object. When an object loses heat then Q is negative. |
When two objects, at different temperatures are placed next to each other there will be a transfer of heat.
|
Exam Hint : When asked to define heat or state what you understand by heat , it should always be mentioned that heat supplied to the system are considered to be positive values. |
|
Typical Exam Question A kettle is filled with 2.0kg of water. (a) Calculate how much energy is required to increase the temperatureof the water from 20 0C to boiling point, 100 0C. [3] (b) If the kettle is left running so that it supplies another 12000J ofenergy, how much of the water will have evaporated and turned from a liquid into a vapour. [2] Specific heat capacity of water = 4200 Jkg-1 0C-1 Specific latent heat of vaporisation of water = 2.3 x 106 Jkg-1 (a) A straight substitution of figures into our equation for specific heatcapacity is all that is required. The equation has been rearranged to make the change in heat energy, Q, the subject of the equation. Care must be taken to include the change in temperature of the water. Change in temperature: ∆θ = final temperature – initial temperature = 100 – 20 = 80 oC Heat energy supplied, Q = mc∆θ = 2 × 4200 × 80 = 672,000 J
(b) Again, to answer the question, all that is required is the substitutionof values into the equation for specific latent heat. The equation has been rearranged to give mass as the subject of the equation. Mass evaporated: Q (12000)
As would be expected, this is not a large mass of water Note how, in each of these equations, the values for energy are positive as energy has been supplied to the water. |
|
Specific heat capacity is the amount of heat energy needed to increase the temperature of 1 kg of the material by 1 oC. Q Q = heat energy supplied (J) c = m∆θ c = specific heat capacity (Jkg-1 oC-1or Jkg-1K-1) m = mass of material (kg) ∆θ = change in temperature (oC) = final temperature - inital temperature |
Heat will be transferred from the hotter object to the cooler object. If we concentrate on just one of those objects, energy supplied to it by heating has two possible consequences: - a change in its temperature and/or a change of state, from liquid to gas for example.
Heat supplied to an object or removed from it can
lead to a change in temperature of the object or a change of state of the
object, or even a combination of both of these things.
If an object has heat supplied or removed such that it results in a change in temperature then the size of the change in temperature will be governed by the specific heat capacity of the object. This is the amount of heat required to increase the temperature of 1 kg of the material by 1 oC.
If the temperature of the substance is increasing then heat is being supplied to the substance and the change in heat , Q, is positive. If the substance is cooling down then it is losing energy and the change in heat energy, Q, is negative.
www.curriculumpress.co.uk
|
Typical Exam Question Air is enclosed in a container that has a moveable piston. The container has an initial volume of 7.50 x 10-4 m3. A constant force of 125N is applied to the piston so that it moves a distance of 4.50cm, compressing the gas. The pressure of the gas remains at 100,000Pa throughout the compression. (a) Calculate the work done in moving the piston. [2] (b) Calculate the final volume of the gas, stating any assumptionthat you make. [4] (a) A force and distance have been given in the question so that thesenumbers can be substituted into our general equation for work done. Care must be taken to change the units of distance into metres before substitution into the equation. The final answer has also been quoted to the same number of significant figures as given in the question. W = Fx = 125 × 0.045 = 5.625 = 5.63J (b) The question provides a pressure for the compression, and a valuefor work done has just been calculated. We can use these values to calculate the change in volume of the gas. Note how the value for work done calculated in the first part of the question has a positive value as it represents work being done on the gas. As the question suggests, an assumption has been made that all the work done in pushing the piston has been transferred to the gas. Note how all of the significant figures from the last calculation have been used when substituting into this equation. W = p∆V ∆V
= W p 100,000 Knowing the change in volume and the initial volume, the final volume can now be calculated. Final volume = initial volume - change in volume = 7.5 × 10-4 – 5.625 × 10-5 = 6.9375 × 10-4 = 6.94 × 10-4 m3 Assumption: All of the work done in pushing the piston is transferred to work done on the gas. |
|
W = Fx W = work done (J) F = force applied (N) x = distance moved (m) |
Work DoneWork is done on a material whenever a force that is being applied to the material moves through a distance. An example of work being done on a solid is when a force is being used to move one object across another object against friction. In this instance, the work done on the solid would cause the two solid objects to increase in temperature. Work can also be done on fluids such as a gas being compressed. When the piston of a sealed bike pump is pushed in, as the force moves through a distance it will increase the temperature of the gas as well as store some energy in the gas. This stored energy could be released by letting go of the piston. The piston would spring back out as the gas expands.
When work is done, energy is transformed from one form to another. Work done has the same units of energy, joules (J).
The work done on a gas is also related to the pressure and volume of a gas. Consider a gas that is enclosed in a cylinder. The pressure of the gas inside the cylinder is P. One wall of the cylinder is moveable like a piston. A side
Now, imagine a force is exerted on the moveable wall that squashes the gas a little, moving the piston a small distance. The force has moved through a distance, doing work on the gas.
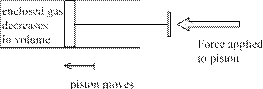
through a distance
The amount of work done on the gas is given by its pressure multiplied by its change in volume.
|
W = work done (J) W = p∆V P = pressure (pa) ∆V= distance moved (m) The pressure of the gas is assumed to stay the same when using this equation. |
• When work is being done on a gas (in other words it is being compressed), work done is given a positive sign.
• When work is being done by a gas, (in other words the gas is expanding and pushing back its boundaries), it is given a negative sign.
Note how the symbol, ∆, which is the greek letter delta, is used to represent a change in volume. This is in the same way as ∆θ represents a change in temperature.
Internal Energy is the term used to describe all of the energy contained in a material and it is given the symbol, U. Any change in the internal energy of a material is given the symbol, ∆U. There are two forms of energy that can make up the internal energy of a material:
(i) Potential energy. This is the energy stored in the stretched or compressed bonds between the molecules of a material.
(ii) Kinetic energy. This is the energy that the molecules in a material have because they are moving. In a solid, this movement is vibrational movement centred around a fixed position. In a liquid or a gas this movement is linear as the molecules travel in straight lines in between collisions with other molecules or the sides of the container. • In solids there is a roughly equal split between the potential and kinetic energy.
• In a liquid, the majority of the internal energy is made up of the kinetic energy of the molecules although there is still some potential energy.
• In an ideal gas, there are no forces of attraction between the molecules, so there is no potential energy and all of the internal energy is made up of the kinetic energy of the fast-moving gas molecules.
|
|
www.curriculumpress.co.uk
|
Exam Hint: To avoid making errors with units of values used in calculations it is best to change all units into standard units before starting any calculation. Some common standard units used in this topic are: Energy – Joules (J), time – s, volume – m3, pressure – pascals (pa) |
|
Typical Exam Question (a) The First Law of thermodynamics can be stated in the form: ∆U = Q+ W . State what you understand by the term ∆U in this law. [1] (b) The diagram below shows a freezer. The fluid inside the pipesevaporates at A, is compressed by the pump at B and cools as it passes through the pipes at C.
(i) Explain where the fluid is gaining or losing heat energy inthe diagram. [2] (ii) Explain where the fluid is doing work or is having work done on it in the diagram. [2] (c) 3.5 kg of water with a temperature of 20oC is placed in the freezer. It takes 2.0 hours to freeze the water without cooling it below 0oC. (i) How much energy is removed from the water? [5] (ii) What is the power of the freezer. [2] Specific latent heat of fusion for water = 3.4 x 105Jkg-1 (a) ∆U is the change in internal energy of the substance. A positive value for ∆U represents an increase in internal energy.
(b) (i) The fluid is gaining latent heat energy inside the freezer, at A, as itchanges from a liquid to a gas. The fluid loses heat energy at C where it cools down. (ii) The fluid is having work done on it where it is being compressedin the pump at B. The fluid is doing work at A where it is expanding.
(c) (i) This part of the question requires two initial calculations. One to calculate the energy removed because the water is cooling down and one to calculate the energy removed because the water is changing into a solid. Considering the cooling process first we can use our equation for specific heat capacity, rearranged to make energy the subject of the equation. The change in temperature is from 20 oC to 0 oC. Q = mc∆θ = 3.5 × 4200 × 20 = 294,000 J Now we can calculate the energy removed from the water to change it into a solid using our equation for latent heat. Q = ml = 3.5 × (3.4 × 105) = 1190000 J The total energy removed from the water is the sum of these. Total heat energy removed = 294,000 + 1190000 = 1484000 = 1.5 × 106 J (to 2 significant figures as given in the question). (ii) To calculate the power of the freezer, we need to use the equation Energy Power = Time remembering to change the time into seconds. E 1.5 × 106 P = = = 2.1 kW t 2083 |
|
A simple example in the use of this equation would be to consider a cleaner scrubbing the inside of a fridge. As he scrubs, he is applying a force through a distance and performing 50J of work on the interior of the fridge. At the same time the interior of the fridge is being cooled and has had 30J of heat energy removed. If we consider the change in internal energy of the interior of the fridge by using the first law of thermodynamics we must first decide the sign of the change in heat energy and work done. The heat energy supplied to the fridge interior, Q = -30J The work being done by the fridge interior, W =+50J Increase in internal energy of the fridge interior; ∆U = Q + W = -30 +50 = 20J This increase in internal energy would be seen as an increase in the temperature of the fridge interior. |
|
Exam Hint : Decide and write down the signs of work done and energy before using the values in the first law of thermodynamics. |
|
|
The three concepts that have so far been covered by this Factsheet - energy transferred by heating, work done and internal energy - are linked by the first law of thermodynamics.
A change in the internal energy of
a substance will occur if it gains or loses heat energy and also if the
substance receives or does work on its surroundings or has work done on it.
∆U = Q+ W ∆U = increase in internal energy of the substance (J)
Q = heat energy supplied to the substance (J)
W = work done on the substance (J)
Hence, supplying the substance with heat energy, making Q positive will increase the internal energy of the substance and ∆U will be positive. Also, doing work on the substance, making W positive, will also increase the internal energy of the object, again making ∆U positive.
Similarly, if energy is removed from a substance and it is
allowed to cool, making Q negative, it will experience a decrease in internal
energy and ∆U
will be negative. Also if the substance does work on the surrounding, making W
negative, it will experience a decrease in internal energy, and ∆U will be
negative.
www.curriculumpress.co.uk
|
Exam Workshop This is a typical poor student’s answer to an exam question. The comments explain what is wrong with the answer and how they can be improved. The examiner’s answer is given below. (a) The first law of thermodynamics may be written as: ∆U = Q+ W. State what you understand by each of the terms in the equation.[3] ∆U is the change in internal energy Q is heat energy W is work done✗✗ 1/3
(b) 10 g of water occupying a volume of 10 cm3 is heated in a kettle from 20 oC to 100 oC and then evaporated into steam, which occupies a volume of 0.0016 m3. (i) Calculate the heat energy required to increase thetemperature of the water to 100oC. Specific heat capacity of water = 4,200 Jkg-1oC-1 [2]
Q = mc∆θ = 10 × 4200 × 100 = 4,200,000J ✗ 1/2
(ii) Calculate the heat energy required to turn the water at 100oC into steam. Latent heat of vaporisation for water = 2.3 × 106Jkg-1 [2] Q = ml = 10 × 2.3× 106 =2.3 × 107J ✗ 1/2
(iii) What is the total heat energy supplied to the water? [1] Total energy = 4,200,000 +2.3 × 107 = 2.72 × 107J 1/1
(c) Calculate the work is done by the steam as it expands. [2] W = p∆V = 101,000 × 0.0016 = 161.6J 2/2
(d) Calculate the increase in internal energy of the water for theentire process. [3]
∆U = Q + W = 2.72 × 107 + 161.6 = 27,200,161.6 J ✗✗ 1/3
Examiner’s Answers (a) ∆U is the increase in internal energy a substance. Q is energy supplied to the substance by heating. W is work done on the substance. (b) (i) Q = mc∆θ = 0.01× 4200× (100-20) =3360J ( quote 3.4 × 103 J) (ii) Q = ml = 0.01× (2.3 × 106) = 23,000J (quote 2.3 × 104 J) (iii) Total heat energy supplied = 3360 + 23,000 = 26,360 = 26,400J (quote 2.64 × 104 J) (c) W = p∆V = 101,000 × 0.0016 = 161.6J (quote 1.6 × 102 J) (d) ∆U = Q + W = 26360 - 161.6 =26,198.4 = 26,200J |
1. What is specific heat capacity?
2. What is the difference between latent heat of vaporisation and latent heat of fusion.
3. When a substance changes from a liquid to a solid, does it receive heat energy or give out heat energy?
4. What sign, positive or negative, is given to the value for the work done by a gas that expands?
5. What two types of energy generally make up the internal energy of a substance? What type of substance only contains one of these types of energy and which is it?
6. What do the three terms represent in the first law of thermodynamics?
1. How much heat energy will be supplied to 1.5kg of water when it is heated from 20oC to 80oC? Specific heat capacity of water = 4,200Jkg-1oC-1.
2. How much heat energy will have to be supplied melt to 0.5kg of ice? Specific latent heat of fusion of ice = 3.4 × 105 J kg-1
3. (a) A gas is allowed to expand at a constant pressure of 150,000Pa from 5m3 to 15m3. What work has been done?
(b) If the gas also receives 3 × 106 J of energy by heating what is the increase in internal energy of the gas?
4. A man drags a crate across the floor of his refrigerated lorry. The crate loses 150J of internal energy and has 350J of energy removed from it by the cold surroundings.
(a) Calculate the work done on the crate.
(b) If the force exerted on the crate is 50N, calculate the distance movedby the crate.
Qualitative Test Answers
The answers can be found in the text
1. Q = mc∆θ = (1.5)(4200)(80-20) = 378,000J
2. Q = ml = (0.5)(-3.4 x 105) = -1.7 x 105J. Note how the answer is negative as the ice is giving out energy and not supplying it.
3. (a) W = p∆V = (150000)(5-15)=-1,500,000J. Again, note the minus sign showing that the gas has been doing work.
(b) ∆U = Q+ W = 3 x 106 – 1,500,000 = 1,500,000J
4. (a) W = ∆U – Q = -150 –(-350) = 200J (b) x = W/F = (200)/(50) = 4m
Acknowledgements:
This Physics Factsheet was researched and written by Jason Slack
The Curriculum Press,Unit 305B, The Big Peg,120 Vyse Street, Birmingham, B18 6NF Physics Factsheets may be copied free of charge by teaching staff or students, provided that their school is a registered subscriber.
No part of these Factsheets may be reproduced, stored in a retrieval system, or transmitted, in any other form or by any other means, without the prior permission of the publisher.
ISSN 1351-5136
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
