
|
Ta’rif. Agar to‘g‘ri chiziq tekislikdagi ikki o‘zaro kesishuvchi to‘g‘ri chiziqqa perpendikulyar bo‘lsa, bu to‘g‘ri chiziq tekislikka ham perpendikulyar bo‘ladi. |
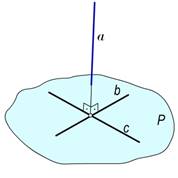
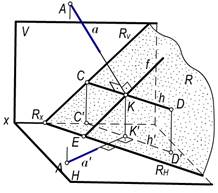
Bunda bÌP va cÌP, bÇc hamda a^b va a^c bo‘lsa, a^P bo‘ladi (113-rasm). Demak, tekislika perpendikulyar bulgan to‘g‘ri chiziq tekislikning asosiy chiziqlariga ham perpendikulyar bo‘ladi. Faraz qilaylik, a to‘g‘ri chiziq tekislikning h gorizontali va f frontaliga perpendikulyar bo‘lsin (114-a, rasm).
To‘g‘ri burchakning
proyeksiyalanish xususiyatiga muvofiq ![]() AKD=90o bo‘lib, KD∥H bo‘lgani uchun bu to‘g‘ri
burchakning gorizontal proyeksiyasi
AKD=90o bo‘lib, KD∥H bo‘lgani uchun bu to‘g‘ri
burchakning gorizontal proyeksiyasi ![]() A′K′D′=90o bo‘ladi. Demak, A′K′^C′D′
yoki a′^h′ bo‘ladi.
A′K′D′=90o bo‘ladi. Demak, A′K′^C′D′
yoki a′^h′ bo‘ladi.
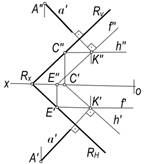
P tekislikning h gorizontalini gorizontal proyeksiyasi h′||PH bo‘lgani uchun a′^PH bo‘ladi. Shuningdek, a″^f″ yoki a″^PV bo‘lishini isbotlash qiyin emas (114,a-rasm). Demak, a^P bo‘lsa, a′^ h′ va a″^ f″ yoki a′^PH va a″^PV bo‘ladi (114,b-rasm).
Fazoda to‘g‘ri chiziq tekislikka perpendikulyar bo‘lishi uchun, uning gorizontal proyeksiyasi tekislik gorizontalining gorizontal proyeksiyasiga, frontal proyeksiyasi esa tekislik frontalining frontal proyeksiyasiga va profil proyeksiyasi tekislik profilining profil proyeksiyasiga perpendikulyar bo‘lishi kerak.
Agar tekislik chizmada izlari bilan berilgan bo‘lsa, unga perpendikulyar bo‘lgan to‘g‘ri chiziqning bir nomli proyeksiyalari tekislikning bir nomli izlariga mos ravishda perpendikulyar bo‘ladi (115-rasm).
To‘g‘ri chiziq va tekislikning o‘zaro perpendikulyarlik shartidan foydalanib ko‘pgina metrik masalalarni yechish mumkin.
a) b)
113-rasm 114-rasm
1-masala. DABC bilan berilgan tekislikning A uchidan unga perpendikulyar o‘tkazilsin (116-rasm).
Echish. Masalani quyidagi algoritm bo‘yicha yechamiz.
1. DABC (DA′B′C′, DA″B″C″) tekislikning h(h′, h″) gorizontali va f(f′, f″) frontali o‘tkaziladi.
2. Tekislikning A nuqtasining A′ va A″ proyeksiyalaridan ixtiyoriy uzunlikda A′E′^h′ va A″E″^f″ qilib perpendikulyarning proyeksiyalarini yasaladi.
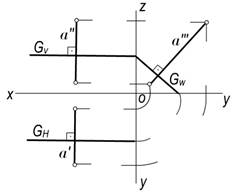
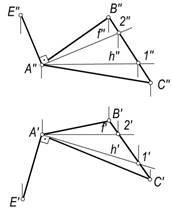
115-rasm 116-rasm
2-masala. A(A′, A″) nuqta orqali l(l′, l″) to‘g‘ri chiziqqa perpendikulyar tekislik o‘tkazilsin (117-rasm).
Echish. Buning uchun:
· A nuqtaning A′ va A″ proyeksiyalaridan h′^l′ va h″||Ox qilib izlangan tekislik gorizontalining proyeksiyalarini o‘tkaziladi;
· A nuqtaning A′ va A″ proyeksiyalaridan f ′||Ox va f ″^l″ qilib tekislik frontalining proyeksiyalarini o‘tkaziladi;
· hosil bo‘lgan hÇf(h′Çf′ L h″Çf″) kesishuvchi chiziqlar izlangan tekislikni ifoda qiladi.
Tekislikning gorizontali h ^ l va frontali f ^ l bo‘lgani uchun bu tekislik l to‘g‘ri chiziqqa perpendikulyar bo‘ladi.
3-masala. A(A′, A″) nuqta orqali o‘tuvchi va b(b′, b″) to‘g‘ri chiziqqa perpendikulyar bo‘lgan tekislikning izlari qurilsin (118–rasm).
Echish.
· A nuqtaning A′ va A″ proyeksiyalaridan h′∋A′ va h′^b′ va h″∋A″ va h″∥Ox qilib tekislikning gorizontali o‘tkaziladi (119-rasm).
· gorizontalning frontal B izining B′ va B″ proyeksiyalarini yasaladi.
· Q tekislikning QV frontal izini QV∋B″ va QV^b″ qilib o‘tkaziladi. Tekislikning QH gorizontal izini esa QX dan QH'QX va QH^b′ (yoki QH∥h′) qilib o‘tkaziladi.
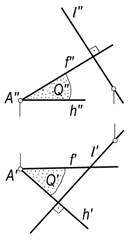
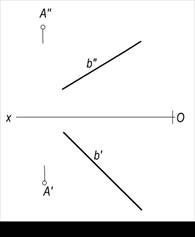
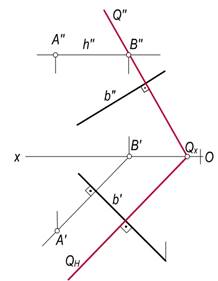
117-rasm 118-rasm 119-rasm
Natijada, QH^b′ va QV^b" bo‘lgani uchun Q^b bo‘ladi. Bu misolni tekislikning frontal chizig‘ini o‘tkazish yo‘li bilan ham yechish mumkin.[1]
 Nuqta
va tekislik orasidagi masofani aniqlash. Nuqtadan
tekislikkacha bo‘lgan masofa nuqtadan tekislikka tushirilgan perpendikulyarning
uzunligi bilan aniqlanadi. Bu perpendikulyarning uzunligini aniqlash uchun
uning tekislikdagi asosini yasash zarur.
Nuqta
va tekislik orasidagi masofani aniqlash. Nuqtadan
tekislikkacha bo‘lgan masofa nuqtadan tekislikka tushirilgan perpendikulyarning
uzunligi bilan aniqlanadi. Bu perpendikulyarning uzunligini aniqlash uchun
uning tekislikdagi asosini yasash zarur.
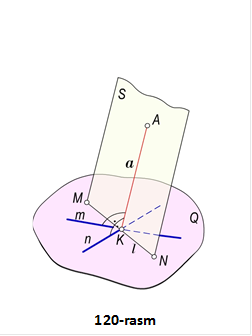
Nuqtadan tekislikkacha bo‘lgan masofani qo‘yidagi yasash algoritmi bo‘yicha aniqlanadi (120-rasm).
· A nuqtadan Q tekislikka a perpendikulyar o‘tkaziladi: a ' A va a ^ Q.
· Bu perpendikulyarning Q tekislik bilan kesishgan K nuqtasi (asosi) aniqlanadi: K=aÇQ.
Buning uchun:
· a perpendikulyardan o‘tuvchi yordamchi S É a tekislik o‘tkaziladi;
· Q va S tekisliklarning l kesishish chizig‘i yasaladi;
· a perpendikulyarning tekisliklarning kesishish chizig‘i l bilan kesishgan K nuqtasi topiladi: K=a∩l. Chizmadagi AK kesma A nuqtadan Q tekislikkacha bo‘lgan izlangan masofa bo‘ladi.
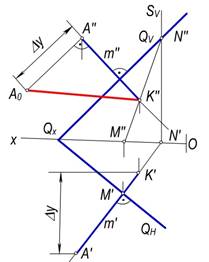
1-masala. Berilgan A (A′, A″) nuqtadan Q (QH, QV) tekislikkacha bo‘lgan masofani aniqlansin (121-rasm).
Yechish. Yuqorida keltirilgan yasash algoritmiga asosan:
· A nuqtaning A′ va A″ proyeksiyalaridan Q tekislikning QH va QV izlariga mos ravishda perpendikulyarning a′ va a″ proyeksiyalari o‘tkaziladi: a′'A′, a′^QH va a″'A″, a″^QV.
· Bu perpendikulyarning Q tekislik bilan kesishish nuqtasining proyeksiyalarini aniqlash uchun:
o a perpendikulyardan yordamchi gorizontal proyeksiyalovchi S(SH,SV) tekislik o‘tkaziladi;
o Q va S tekisliklarning kesishish chizig‘i MN(M′N′,M″N″) bilan a(a′,a″) perpendikulyarning kesishish nuqtasi K ning K′ va K″ proyeksiyalarini aniqlanadi.
· Chizmada hosil bo‘lgan A′K′ va A″K″ izlangan masofaning proyeksiyalari bo‘ladi. Bu masofaning haqiqiy o‘lchami to‘g‘ri burchakli DA0A″K″ ning A0K″ gipotenuzasi bo‘ladi.
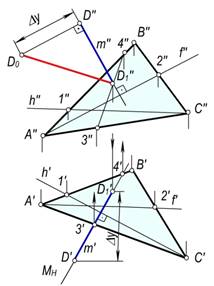
2-masala. D(D′, D″) nuqtadan DABC(DA′B′C′, DA″B″C″) tekislikkacha bo‘lgan masofa aniqlansin (122-rasm).
Yechish. Masalani quyidagi yasash algoritmi asosida yechiladi.
· DABC tekislikning gorizontal va frontal chiziqlarining proyeksiyalari o‘tkaziladi.
· D nuqtaning D′ va D″ proyeksiyalaridan perpendikulyarning m′ va m″ proyeksiyalari m′'D′, m′^h′ va m″'D″, m″^ f ″ qilib o‘tkaziladi.
· Perpendikulyarning DABC tekislik bilan kesishgan nuqtasi D1 ning D1′ va D1″ proyeksiyalarini aniqlanadi.
121-rasm 122-rasm
· m perpendikulyardan yordamchi gorizontal proyeksiyalovchi M(MH, MV) tekislik o‘tkaziladi;
· DABC va M tekisliklarning kesishish chizig‘ining 3′4′ va 3″4″ proyeksiyalarini yasaladi;
· tekisliklarning kesishish chizig‘i proyeksiyalari 3′4′ va 3″4″ bilan m′, m″ perpendikulyarning kesishish D1 nuqtasining D1′ va D1″ proyeksiyalarini aniqlanadi: D1″=m″Ç3″4″ va D″Îm″
Chizmada hosil bo‘lgan D′D1′ va D″D1″ proyeksiyalar izlangan DD1 masofaning proyeksiyalari bo‘ladi. Uning haqiqiy o‘lchami to‘g‘ri bo‘rchakli DD0D″D1″ning D0D1″ gipotenuzasidan iborat bo‘ladi.
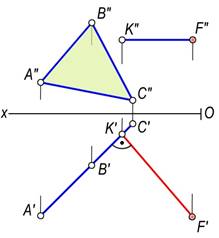
123-rasm 124-rasm
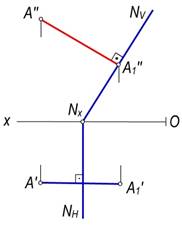
Agar tekislik xususiy vaziyatda berilsa, u holda berilgan nuqtadan tekislikkacha bo‘lgan masofani aniqlash uchun qo‘shimcha yasashlar talab qilinmaydi. Masalan, A(A′, A″) nuqtadan N(NH, NV) frontal proyeksiyalovchi tekislikkacha bo‘lgan masofaning haqiqiy o‘lchami (123-rasm) nuqtaning frontal A″ proyeksiyasidan tekislikning NV frontal iziga tushirilgan perpendikulyarning A″K″ frontal proyeksiyasiga teng bo‘ladi.
124-rasmda F(F′, F″) nuqtadan gorizontal proyeksiyalovchi DABC(DA′B′C′, DA″B″C″) tekislikkacha bo‘lgan masofani aniqlash tasvirlangan.[2]
Скачано с www.znanio.ru
[1] Sh.Murodov va boshqalar “Chizma geometriya” darslik “Iqtisod-moliya”.2006 yil, 75-77 betlar
[2] Sh.Murodov va boshqalar “Chizma geometriya” darslik “Iqtisod-moliya”.2006 yil, 78-80 betlar
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.