Поделиться
ТРАПЕЦИЯ.docx
ТРАПЕЦИЯ
Цели: ввести понятия «трапеция», «равнобокая трапеция», «прямоугольная трапеция»; рассмотреть решение задач, в которых раскрываются свойства трапеции.
Ход урока
I. Анализ ошибок, сделанных в самостоятельной работе.
Устно: определите х, у, z.
|
1)
|
110° + 70° = 180° тогда х + х + 20° = 180°, х = 80°. |
|
2)
|
у = 100°. |
|
3)
|
140° + 40° = 180° тогда 120° +
|
II. Изучение нового материала.
1. Вспомнить с учащимися определение параллелограмма.
2. Рассмотреть такой четырехугольник, у которого две противолежащие стороны параллельны, а две другие – непараллельны.
3. Определение трапеции и ее элементов (рис. 161 из учебника).
4. Виды трапеции (рис. 162 из учебника).
5. На закрепление понятия можно предложить учащимся следующие вопросы:
Какие четырехугольники на рисунке являются трапециями? Назовите их основания и боковые стороны.
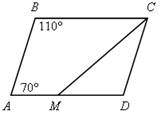
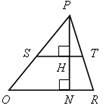
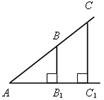
а) б) в)
III. Решение задач.
№ 385 (решена в учебнике), № 386 (по теореме Фалеса). Можно после решения этой задачи дать определение средней линии трапеции.
IV. Итоги урока.
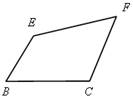
1. АВСD, ВЕFC – трапеции.
2. Частные виды трапеции:
|
Прямоугольная трапеция |
Равнобокая
трапеция |
||
|
3.
В решении задач на трапецию можно использовать свойства углов при
параллельных прямых и секущей |
|
||
|
|
|
||
|
|
|
||
4. Применение теоремы Фалеса в трапеции:
|
а) ВС || MN || KР || QS || АD и МВ = МK = KQ = QA, то CN = NP = PS = SD; б) МВ = МK = KQ = QA и CN = NP = PS = SD, то ВС || MN || KP || QS || AD. |
|
Домашнее задание: вопросы 10, 11, с. 114; № 386, 387,390.
Дана трапеция MPOK с основаниями МK и ОР.
1)
Найти углы трапеции, если 
М
= 72°, О = 105°.
2)
Найти ОРK и РОМ, если ОМK
= 38°, РKM = 48°.
3) углы 
МKN
(N – точка пересечения диагоналей трапеции), если ОРK = 72°, РОМ = 48°.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
