Треугольник( основные свойства и теоремы)

Треугольник-это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых отрезками. Три точки называются вершинами, а отрезки - сторонами. Существует три вида треугольников: остроугольный, прямоугольный и тупоугольный.

В треугольнике существуют три «замечательных» отрезка, которые обладают особыми свойствами, остановимся на них подробнее.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Перечислим свойства медианы треугольника:

1.     Медиана делит треугольник на два равновеликих треугольника.

2.     Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины. Точка пересечения медиан является центром тяжести треугольника.

3.     Медиана прямоугольного треугольника, проведенная из вершины прямого угла равна половине гипотенузы.

4.     Медиана, проведённая из вершины прямого угла к гипотенузе, разбивает треугольник на два равнобедренных треугольника.

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Перечислим свойства высоты треугольника:

1.     Высоты треугольника пересекаются в одной точке, называемой ортоцентром.

2.     Высота h треугольника, проведенная к стороне а может быть легко вычислена, если известна его площадь S : .

3.     высота прямоугольного треугольника с катетами a и b, опущенная на гипотенузу с, может быть вычислена по формуле: .

4.     Высота треугольника, опущенная из вершины прямого угла на гипотенузу, является средним геометрическим отрезков, на которые основание высоты делит гипотенузу.

Биссектрисой треугольника называется отрезок, исходящий из вершины угла и делящий его на две равные части.

Перечислим биссектрисы треугольника:

1.     Три биссектрисы треугольника пересекаются в одной точке, которая есть центр вписанной окружности.

2.     Биссектриса внутреннего угла треугольника делит противолежащую этому углу сторону на отрезки, пропорциональные прилежащим сторонам.

3.     Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

А теперь рассмотрим одну полезную теорему о треугольнике и секущей, которая называется теорема Менелая.

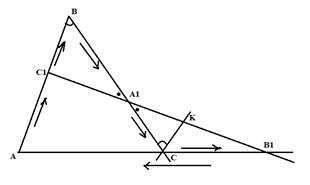Пусть точка  лежит на стороне , точка - на стороне , а точка - на продолжении стороны  за точку  .

Если точки , ,  лежат на одной прямой(см. рис.), то выполняется равенство