
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Ю.А.Каракулев, А.Н.Иванов
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ
С ПРИМЕНЕНИЕМ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
Учебное пособие

2010
УДК 681.3
Каракулев Ю.А., Иванов А.Н. Руководство к решению задач с применением электронных таблиц EXCEL: Учебное пособие.- СПб. СПб ГУ ИТМО, 2010. – 48 с.
Учебное пособие рекомендуется для использования в дисциплинах “Прикладная информатика”, “Введение в специальность”. Его основная тема – организация данных в виде таблиц, работа с формулами и встроенными функциями, задачи оптимизации, обработка результатов измерений, представление данных из таблиц в графическом виде.
Каждый раздел начинается с изложения теоретического материала и завершается практическим заданием для выполнения.
Пособие предназначено для студентов, обучающихся по направлению 200200 "Оптотехника" и специальности 200203 "Оптико-электронные приборы и системы"
Рекомендовано к печати Ученым советом ФОИСТ от 9 марта 2010 г., протокол № 7

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена Программа развития государственного образовательного учреждения высшего профессионального образования «СанктПетербургский государственный университет информационных технологий, механики и оптики» на 2009–2018 годы.
© Санкт-Петербургский государственный университет информационных технологий, механики и оптики, 2010
© Ю.А.Каракулев, А.Н.Иванов, 2010
Введение. . . . . . . . . . . . . . . . . . . . . 4
1. Работа с электронными таблицами. Общие сведения и понятия. . . 5
2. Основные приемы работы с таблицами . . . . . . . . . . 6
2. 1. Ввод данных. . . . . . . . . . . . . . . . . . 6
2. 2. Форматирование таблицы. . . . . . . . . . . . . 8
2. 3. Встроенные функции. . . . . . . . . . . . . . .11
3. Решение задач с применением формул и функций. . . . . . 14
3. 1. Численные вычисления производной и определенного
интеграла. . . . . . . . . . . . . . . . . . 14
3. 2. Решение линейных уравнений. . . . . . . . . . . . 17
4. Решение задач оптимизации. . . . . . . . . . . . . 19
5. Решение статистических задач. . . . . . . . . . . . . 24
5. 1. Обработка экспериментальных данных. . . . . . . . 24
5. 2. Оценка истинности предположений. . . . . . . . . 29
6. Создание диаграмм. . . . . . . . . . . . . . . . . 35
6. 1. Диаграммы типа график. . . . . . . . . . . . . 35
6. 2. Построение круговой диаграммы . . . . . . . . . . 37
6. 3. Трехмерные графики. . . . . . . . . . . . . . 38
6. 4. Трендовый анализ. . . . . . . . . . . . . . . 40
Список литературы. . . . . . . . . . . . . . . . . 45
Введение
“Если вычислений много, а времени мало, то доверьтесь электронным таблицам”. Этому постулату как нельзя лучше отвечают вычислительные возможности электронных таблиц Excel, которые без оговорки можно назвать безграничными.
Хотя в настоящее время появилось огромное количество литературы по Excel, практика показывает, что материал в профессиональных издания излишне теоритизирован. Практические задачи и примеры страдают уклоном в области экономики и финансов. Это не дает представления о возможности использования Excel в других отраслях деятельности.
Особенностью Excel является возможность применения формул для описания связи между значениями различных ячеек. Расчет по заданным формулам выполняется автоматически. Изменение содержимого ячейки приводит к пересчету значений всех ячеек, которые с ней связаны формульными отношениями, к обновлению всей таблицы в соответствии с изменившимися данными. Применение Excel упрощает работу с данными и позволяет получать результаты без проведения расчетов вручную или специального программирования. Excel можно эффективно использовать для:
- проведения расчетов над большими наборами данных;
- автоматизации итоговых вычислений;
- табулирования функций;
- решения задач путём подбора значений параметров;
- проведения поиска оптимальных значений параметров;
- обработки результатов экспериментов;
- построения диаграмм и графиков по имеющимся данным.
Пособие содержит расчетные задачи, которые часто приходится решать студентам в процессе обучения при выполнении лабораторных работ, домашних заданий, курсовых проектов и выпускных работ.
Каждый раздел учебного пособия начинается с изложения решения конкретной задачи соответствующей тематики. В конце раздела предлагаются задачи для самостоятельного решения. Некоторые задачи заимствованы из литературных источников, приведенных в списке литературы.
Авторы приносят извинения за недостаточно подробное разъяснение некоторых вопросов работы в среде электронных таблиц Excel из-за ограниченного объема пособия. Надеемся, что этот недостаток легко устраним в уже изданной по данной тематике литературе.
Структура экрана электронных таблиц Excel (Excel), показанная на рис.1, похожа на структуру других приложений Windows. Отличием является строка формул, которая предназначена для работы с содержимым ячеек. Строка формул состоит из трех частей. В левой части – поле имен указывают адрес активной ячейки. На рис.1 это ячейка В2. Правая часть отображает содержимое активной ячейки, которое можно редактировать либо непосредственно в строке формул, либо в самой ячейке. В центре строки расположены кнопки команд для левой и правой части строки
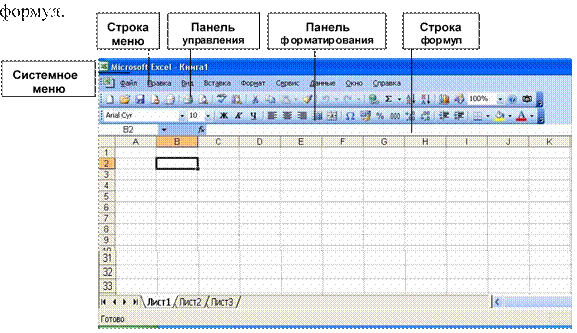
Рис.1. Вид окна электронной таблицы Excel
Excel состоят из листов, которые объединены в книгу. Всего листов 16. Листы обозначаются ярлычками в нижней части экрана: Лист 1, Лист 2 и т.д.
Рабочее поле Excel образовано столбцами и строками. Столбец определяет колонку в Excel. Столбцы нумеруются прописными латинскими буквами в следующем порядке А … Z, AA… AZ, BA… BZ, … Всего столбцов 256. Строка определяет ряд в Exsel. Всего строк 16384. Они обозначены цифрами на левой границе рабочего поля.
Ячейка – элемент Excel, который содержит данные. Каждая ячейка имеет уникальный адрес, состоящий из буквы столбца и номера строки. Например, адрес С3 определяет ячейку на пересечении столбца С и строки 3. Другой способ адресации ячейки – по имени (слово, число, их комбинация). Имя, как адрес активной ячейки, вводится в поле имен. Для присвоения имени активной ячейки необходимо выбрать команду меню Вставка, Имя, Присвоить, окно Присвоение имени. На неактивном листе Excel адрес ячейки обозначается именем листа и адресом ячейки на нем. Например, Лист 2! А7 (обязательно – восклицательный знак).
Блок в Excel – прямоугольная область рабочего поля из смежных ячеек. Адрес блока состоит из адресов противоположных ячеек: левой верхней и правой нижней, разделенных двоеточием. Например, блок В2: С3 представляет область из смежных ячеек В2, С2, В3 и С3 блок В2: В4 – В2, В3 и В4.
Существуют три типа данных, которые вводят в ячейки Excel: текст, число и формула. Для ввода данных необходимо выделить нужную ячейку, набрать данные, а затем нажать <Enter> или клавишу перемещения курсора или значок (∨) в строке формул.
Под вводом текста в Excel понимается набор любых символов:
букв, чисел, знаков. Если текст начинается с числа, то ввод следует начать с символа (′). Запишем в ячейку В3 текст “ Прикладная оптика 90 ”. Видно, что ширина текста больше ширины ячейки, текст занимает место соседней ячейки С3. Но при вводе данных в ячейку С3 предыдущий текст визуально будет обрезан, он сохраняется полностью в ячейке В3.
Числа в ячейку вводятся со знаками
+, –, = или без них. Если под число не хватает места в ячейке, Excel вместо
числа ставят символы (#). При этом число хранится в памяти, либо записывается
в форме экспоненты. Например, 105000000 =1,05Е +08. Десятичная дробь в Excel записывается
через запятую – 1,27. Простая дробь ![]() – набором: < 0 >,<
9 > и 1/3.
– набором: < 0 >,<
9 > и 1/3.
Формула в Excel представляет собой последовательность чисел или ссылок на ячейки, объединенных арифметическими операторами: сложение, вычитание, умножение, деление, возведение в степень или функциями. Формула должна начинаться со знака (=), не должна содержать пробелов. Для ввода в ячейку формулы А2 + С4 надо записать =А2+С4. Результат, как сумма содержимого указанных ячеек, будет получен в ячейке, в которой записана формула.
Ссылки на ячейки в формулах дают возможность использовать данные, находящиеся в разных ячейках, таблицах, листах. При обращении к ячейке возможна относительная и абсолютная адресация. Относительная адресация предполагает постоянство относительного, взаимного положения ячеек и при переходе к другой ячейке сохраняет это расположение на новом месте таблицы. Абсолютная адресация предполагает постоянную адресацию к ячейке, обозначенной знаком ($), независимо от места (адреса) другой ячейки. Варианты возможных обращений к ячейкам показаны в таблице 1.
Варианты адресаций к ячейкам Excel
Таблица 1.
|
Относительная |
Абсолютная |
Положение ячейки |
|
С7 |
$C$7 |
Ячейка на пересечение столбца С и строки 7 |
|
B:B |
$B :$B |
Ячейки столбца В |
|
5 : 5 |
$5:$5 |
Ячейки строки 5 |
|
B3:D5 |
$B$3 :$D$5 |
Область ячеек в столбцах В…D и строках 3…5 |
Ссылка на другие листы рабочей книги Excel осуществляется путем включения в формулу ссылки на лист : Лист3!В7 .
При введении формулы могут возникнуть ошибки, которые приводят к ошибкам в результате вычисления. Наличием ошибки в формуле является появление символа (#), за которым следует текст.
Наиболее распространенные ошибки при введении формул.
Ошибка вида ( # # # ). Причины – применяется формула, результат выполнения которой не умещается в ячейке, вводимое число не умещается в ячейке. Устранение – увеличить ширину столбца, либо изменить формат числа в ячейке. Для чего выбрать команды меню: Формат, Ячейка, Число и указать другой формат.
Ошибка (#ЗНАЧ!). Причина – вместо числового значения введен текст. Например, вычисляем =А2+С2, при этом в ячейке А2 введено число 6, а в ячейке С2 значение «два». Устранение – проверить правильность задания типов аргументов.
Ошибка (#ИМЯ?). Причина – в формуле было удалено или не было определено имя ячейки, либо имеется ошибка в написании имени функции, либо в формулу введен текст, не заключенный в кавычки, либо в ссылке на блок ячеек пропущен знак (:). Устранение - исправить указанные ошибки.
Ошибка (#ССЫЛКА!). Причина – ячейки, на которые ссылается формула, были удалены, либо в ячейках содержится информация других скопированных ячеек. Устранение – изменить формулу, либо восстановить прежнюю информацию ячейки: нажать <отменить> после удаления или копирования содержимого ячейки.
Задача 1. Вычислить по формуле f´= r1 r2 / (( n- 1)⋅ (r2- r1)) фокусное расстояние бесконечно тонкой линзы, где d= 0, толщина по оси; r1= 230, r2= - 480, радиусы кривизны; n=1.5, показатель преломления стекла.
Решение. Значения исходных данных запишем в ячейки А2, В2 и С2. В ячейку В4 запишем расчетную формулу. На рис. 2 расчетная формула Excel показана в строке формул. После нажатия <Enter> в ячейке В4 появится результат расчета 310,99.
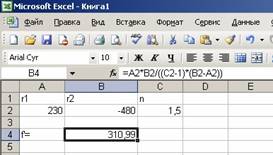
Рис. 2. Решение задачи №1
Задача 2. Вычислить фокусное расстояние системы из двух линз f, если известна формула оптической силы Ф = Ф1 + Ф2 – Ф1 Ф2 d, где f1= 120, f2= 210, для d= 1,5 ; 2,0 и 2,5
Задача 3. Вычислить величину перемещения винта L у винтового механизма при округлении числа π до 3, 4 и 5-го знака после запятой по формуле L = k t / 2 π , где k = 2 (число заходов) , t = 0,75 (шаг резьбы)
Задача 4.
4.1. Укажите формулу Excel, из приведенных
а) В3С7+13; в) =B3*C7+13; c) B1=B3C7+13; d) B3*C7+13
4.2. Какая формула будет получена при копировании ячейки А2 с формулой =D5*H7 в ячейку А5
а) =D5*H7; в) =G5*K7; c) =G8*K10; d) =D8*H10
4.3. В ячейке А2 записано 10, в ячейке В2 записано =А2/5, в ячейке С5 записано =А2+В2. Чему равно значение С5
а) 10; в) 15; c) 5; d) 12.
4.4. Какая формула будет получена при копировании ячейки А2 с формулой =$D5+H$7 в ячейку А5
а) =$D5+H$7; в) =$D8+$H7; c) =$D5+$H$10; d) =$D8+H$10
4.5. Какая формула будет получена при копировании ячейки А2 с формулой =$D5+H$7 в ячейку D5
а) =$D5+H$7; в) =$D8+K$7; c) =$G8+$H10; d) =$D5+K$7
Форматированию элементов Excel предшествует операция– выделение. Чтобы выделить строку (столбец), помещаем указатель на номер (букву) выделяемого элемента и нажимаем левую кнопку мыши. Для выделения всего листа помещаем указатель в ячейку на пересечении обозначенных строк и столбцов. Выделение снимается щелчком в любом месте экрана.
Изменение размеров элементов
Excel. Для того, чтобы изменить размер строки (столбца), при помощи мышки наводят
указатель ( ![]() )
на нижнюю (правую) границу элемента и перетаскивают ее на нужный размер. Чтобы установить
размер строки (столбца) «как раз» по размеру содержимого ячейки, надо подвести
указатель к границе элемента и дважды щелкнуть левой кнопкой мышки. Другой способ
изменения размеров элементов таблицы: выделить нужный элемент и использовать команды
меню Формат, Строка (Столбец), Высота (необходимо указать
высоту числом точно).
)
на нижнюю (правую) границу элемента и перетаскивают ее на нужный размер. Чтобы установить
размер строки (столбца) «как раз» по размеру содержимого ячейки, надо подвести
указатель к границе элемента и дважды щелкнуть левой кнопкой мышки. Другой способ
изменения размеров элементов таблицы: выделить нужный элемент и использовать команды
меню Формат, Строка (Столбец), Высота (необходимо указать
высоту числом точно).
Задача 5. Проделайте форматирование строк таблицы (табл. 2):
1. Последовательно выделяйте строки.
2. Выберите Формат, Строка и требуемые операции из первого столбца.
Форматирование строки таблицы Excel
Таблица 2.
|
Операция |
Описание |
|
Высота |
Определяет новую высоту для выбранных строк |
|
Автоподбор высоты |
Приводит высоту строк таблицы в соответствие с наибольшим шрифтом. Это установка по умолчанию |
|
Скрыть |
Скрывает строки |
|
Отобразить |
Показывает строки, которые были до этого скрыты |
Форматирование ячеек. Каждая ячейка Excel обладает рядом свойств, в том числе форматами отображения информации на экране. Все форматы ячеек отображаются в окне Формат ячеек (рис.3), которое вызывается из меню Формат.
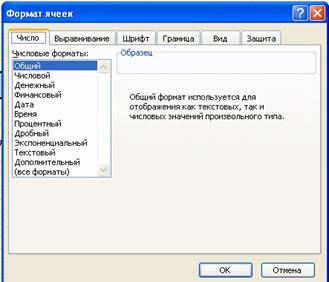
Рис.3. Вид окна Формат ячеек
Формат числа. При вводе числа в ячейку Excel ему присваивается Общий формат. Чтобы задать нужный формат, используйте закладку Число
(рис.3), выберите из списка Числовые форматы формат, который хотите применить к выделенным ячейкам. Вместе с этим в данной закладке можно указать число десятичных знаков и обозначение введенного числа. Пример числа в Денежном формате – 1,30 р. (число десятичных знаков – 2, обозначение – р.) В таблице 3 приведены основные форматы представления чисел в Excel.
Числовые форматы ячеек
Таблица 3.
|
Образец числа |
Форматы ячеек |
|
13,5 |
Общий |
|
13,50 |
Числовой, число десятичных знаков = 2 |
|
13,500 |
Числовой, число десятичных знаков = 3 |
|
13,50 р. |
Денежный, обозначение валюты- р |
|
1 январь, 2010 |
Дата |
|
12:00 |
Время |
|
1350,00 % |
Процентный, число десятичных знаков =2 |
|
13 1/2 |
Дробный, с половинными долями |
|
13 50/100 |
Дробный, с сотыми долями |
|
1,35Е+ 01 |
Экспоненциальный |
|
13,5 |
Текстовый, число воспринимается как текст и не участвует в расчетах при обращении к нему формулы |
|
|
Дополнительные форматы |
|
000014 |
Почтовый индекс |
Задача 6. Заполните таблицу 4 предложенными форматами
Форматы ячеек
Таблица 4.
|
Общий |
Числовой |
Денежный |
Процентный |
|
12.6 |
|
|
|
|
|
|
125,01 р. |
|
Следующая закладка окна Выравнивание позволяет по-разному размещать информацию, занесенную в ячейку. Можно выбрать симметричное расположение информации по горизонтали, по вертикали, расположить текст в несколько строк.
Остальные закладки окна Формата ячеек – Шрифт, Граница, Вид, Защита обеспечивают быстрый доступ к соответствующим опциям форматирования.
Кроме форматирования элементов поля ячеек, строк и столбцов часто бывает полезно использовать несколько рабочих листов Excel. Для систематизации и поиска информации в книге удобно присваивать названиям листов собственные имена, отражающие их смысловое содержание. Например, «исходные данные», «результаты расчетов», «графики» и т. п. Это удобно сделать, воспользовавшись контекстным меню. Нажать правую кнопку мышки на ярлычке листа, Переименовать лист и нажать <Enter >.
Для добавления одного или нескольких новых листов в меню Вставка выбрать команду Лист. Чтобы вставить сразу несколько листов нужно выделить ярлычки необходимого числа листов, удерживая <Shift >, затем из меню Вставка выполнить команду Лист. Обратная операция по удалению листов проводится аналогично. Через контекстное меню, где выбирается команда Удалить.
Полезная операция по перемещению листов – левой кнопкой мыши захватить ярлычок листа и переместить его в нужное место. Если при этом нажать <Ctrl>, произойдет перемещение копии листа, а к имени листа добавится число 2 .
Задача 7. Измените формат всей ячейки В2 на: шрифт – Arial 11; расположение – в центре, по нижнему краю; одно слово в строке; формат числа –“0,00”; граница ячейки – двойная линия
|
|
A |
B |
C |
D |
E |
|
1 |
|
|
|
|
|
|
2 |
|
Показатель преломления стекла К8 - 1.5183 |
|||
Программа Excel содержит более 150 встроенных функций для упрощения расчетов и обработки данных. Пример содержимого ячейки с функцией: =В2+SIN(C7), где В2 и С7- адреса ячеек, содержащих числа, а SIN( ) – имя функции. Наиболее используемые функции Excel:
SQRT(25) = 5 – вычисляет квадратный корень из числа (25) РАДИАНЫ(30) = 0,5 - преобразует 30 градусов в радианы
ЦЕЛОЕ(8,7) = 8 – округляет до ближайшего меньшего целого
ОСТАТ(-3;2) = 1 – оставляет остаток от деления числа(-3) на делитель(2). Результат имеет знак делителя.
ЕСЛИ(E4>0,2;”доп”;”ошиб”) – если число в ячейке Е4 меньше 0,2,
тогда Excel возвращают “доп” (истина), в противном случае – “ошиб”(ложь).
В формуле функции могут быть вложенными друг в друга, но не более 8 раз.
При использовании функции главным является определение самой функции и ее аргумента. В качестве аргумента, как правило, указывается адрес ячейки, в которой записана информация.
Определить функцию можно, набрав текст (значки, числа и т.п.) в нужную ячейку, либо воспользоваться Мастером функций. Здесь для удобства поиска все функции разбиты на категории: математические, статистические, логические и другие. Внутри каждой категории они отсортированы в алфавитном порядке.
Мастер функций вызывается командой меню Вставка, Функция или нажатием пиктограммы ( fx ). В первом появившемся окне Мастера функций (рис.4) определяем Категорию и название конкретной функции, нажимаем <OK>. Во втором окне (рис.5) необходимо определить Аргументы функции. Для этого щелчком кнопки справа от первого диапазона ячеек (Число 1) “прикрываем” окно. Выделяем ячейки, на основе которых будет проводиться вычисление. После этого выделенные ячейки будут занесены в окно первого диапазона . Еще раз нажимаем правую клавишу . Если аргументом является несколько диапазонов ячеек, то действие повторяем. Затем для завершения работы нажимаем <OK>. В исходной ячейке окажется результат вычисления.
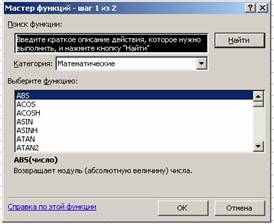
Рис. 4. Вид окна Мастер функций
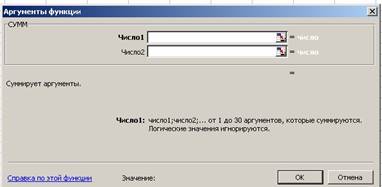
Рис. 5. Окно для задания аргументов выбранной функции
Задача 8. Найти среднее значение ряда чисел: 2,5; 2,9; 1,8; 3,4; 6,1; 1,0; 4,4.
Решение. Вводим числа в ячейки, например, С2:С8. Выделяем ячейку С9, в которую записываем функцию =СРЗНАЧ(С2:С8), нажимаем <Enter>, в С9 получаем среднее значение указанных чисел – 3,15.
Задача 9. Применяя условную логическую функцию ЕСЛИ, составить формулу переименования нечетных числе в «осень», четных - «весна».
Решение. Выбираем столбец для ввода исходных данных – четных
(нечетных) чисел, например, A. В ячейку B3 запишем формулу =ЕСЛИ(ОСТАТ(A3;2)=0;"вес";"осе"). Копируя ячейку B3 вдоль столбца В, получаем результаты анализа записанных в столбце А чисел. Результаты решения задачи представлены на рис. 6.
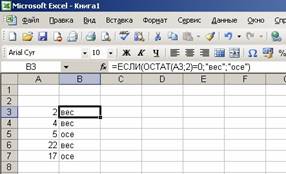
Рис. 6. Решение задачи № 9
Задача 10. Вычислить значение функции y = x3 + sinx – 4ex для x = 1,58.
Решение. Разместим данные в ячейки А2 – х, В2 –у. Решение задачи показано на рис.7 в числовом виде слева и формульном – справа. При решении данной задачи следует обратить внимание на вызов функций SIN и экспоненты для ввода аргумента (см. рис.8).
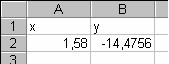
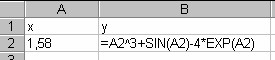
Рис.7. Решение задачи № 10
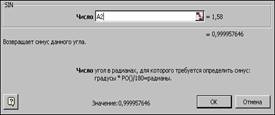
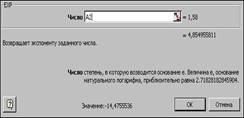
Рис.8. Окна дляввода аргумента функции SIN и EXP
Задача 11. Составьте в Excel математическую модель задачи для
расчета функции y= 1/ ((x- 3) · (x+ 4)), при значениях x= 3 и у= -4 выводить на экран "неопределена", численные значения функции – в остальных случаях.
Задача 12. Составьте в Excel математическую модель задачи:
12.1. для вычисления с корнями
а)√ x3· y2· z / √ x·z ; b) (z · √ z )2 ; c) 3√ x2 · 3√x ; d) √ 5·x5·3-1 / √ 20·x·3-1
12.2. для геометрических вычислений
а) определить углы прямоугольного треугольника, если известны х –
катет, у – гипотенуза ;
b) определить расстояние между двумя точками в декартовой системе
![]() координатах XYZ по формуле d = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2
координатах XYZ по формуле d = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2
с) определить расстояние от точки (x0,y0) до прямой a⋅x + b⋅y + c = 0 по
формуле
d = ⎜a⋅x0+b⋅y0+c⎟ / √ (a2+b2)
d) определить площадь треугольника по координатам вершин по
формуле
S=![]() [(x1 − x3)(y2 − y3)−(x2 − x3)(y1 − y3)]
[(x1 − x3)(y2 − y3)−(x2 − x3)(y1 − y3)]
Задач, которые можно успешно решать с использованием формул и функций Excel, на самом деле много. Рассмотрим задачи, которые в практике наиболее часто решаются с применением электронных таблиц: линейные уравнения и их системы, вычисление численных значений производных и определенных интегралов.
3.1.Численное вычисление производной и определенного
Производной функции y = f(x) называется отношения ее приращения ∆y к соответствующему приращению ∆x аргумента, когда
∆x→ 0 Δy f(x +Δx)− f(x)
![]() =
(1).
=
(1).
Δx Δx
Задача.13. Найти производную функции y = 2x3 + x2 в точке x=3.
Решение. Производная, вычисленная аналитическим методом, равна 60. Вычисление производной в Excel проведем по формуле (1). Для этого выполним последовательность действий:
· Проведем обозначения столбцов: Х – аргументы функции, У – значения функции, У ` – производная функции (рис.9).
· Табулируем функцию в окрестности точки х= 3 с малым шагом, например, 0,001 результаты заносим в столбец Х.
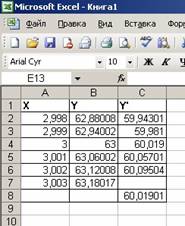
Рис. 9. Таблица вычисления производной функции
· В ячейку В2 введем формулу вычисления функции =2*A2^3+A2^2. · Скопируем формулу до строки 7, получим значения функции в точках табуляции аргумента.
· В ячейку С2 введем формулу вычисления производной =(B3-B2)/ (A3-A2). · Скопируем формулу до строки 6, получим значения производных в точках табуляции аргумента.
Для значения х= 3 производная функции равна значению 60,019, что близко к значению, вычисленному аналитически.
Задача 13. Найти производную функции в указанных точках:
1. Y = 2x2 для х = 3 2. Y= (1-√x)2 / x для х = 0,01
3. Y = Cos(x) для х = 0 4. Y= Sin(x) для х = π/ 2
5. Y = Cos(x) для х = π/ 2 6. Y= Tg(x) для х = 0
7. Y = 4/3 ⋅x3 – 4x для х = 0,2 8. Y= ex ⋅ln x для x=1
9. Y = Cos(x ) / (1- Sin(x)) для х= π /6 10. ( a+ b) /(3- 2x) + (5x4- 1) / (a- b) для х = 0 Определенный интеграл в Excel можно вычислить, используя метод трапеций. В методе трапеций область интегрирования разбивается на отрезки с некоторым шагом и площадь под графиком функции на каждом отрезке считается равной площади трапеции. Тогда расчетная формула принимает следующий вид
b h N−1
SN =![]()
![]() (2),
(2),
где h= (b- a)/ N – шаг разбиения; N – количество точек разбиения.
Для повышения точности количество точек разбиения удваивается, повторно выполняется расчет интеграла. Дробление исходного интервала прекращают, когда достигнута требуемая точность:
3
Задача 14. Вычислить определенный интеграл ∫3x2dx
2
Решение. Для численного вычисления величины определенного интеграла выполним следующие действия:
– выберем N= 5, в ячейке F2 рассчитаем h- шаг разбиения (рис. 10);
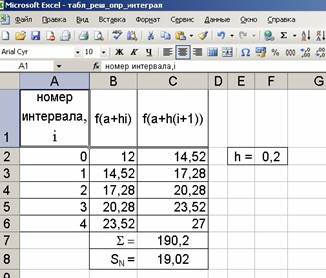
Рис. 10. Вычисление определенного интеграла
· В первом столбце А записываем номер интервала i ;
· В ячейке B2 запишем формулу =3*(2+F2*A2)^2 для расчета первого слагаемого формулы (2);
· В ячейке С2 запишем формулу =3*(2+F2*(A2+1))^2 для расчета второго слагаемого;
· “Протянем” ячейки с формулами на 4 строки вниз по столбцам;
· В ячейку С7 запишем формулу и вычислим сумму слагаемых ,
· В ячейке С8 запишем формулу и вычислим SN искомое значение определенного интеграла 19,02 (значение SN полученное аналитически
19).
Задача. 15. Вычислить определенный интеграл:
1. Y ![]() xd
x 2. Y
xd
x 2. Y ![]() dx
dx
3. Y ![]() dx
4.
Y
dx
4.
Y 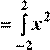 dx
dx
![]() 5
5
dx
5. Y =
∫ ![]() 6. Y
6. Y
1 3x − 2
![]() π x 3x 2
x + 3
π x 3x 2
x + 3
![]() 7. Y =
∫cos cos dx 8.
Ydx
7. Y =
∫cos cos dx 8.
Ydx
0 2 2
Линейные уравнения в Excel можно решить, используя функцию Подбор параметра. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки, не возвратит заданное значение.
Рассмотрим процедуру поиска параметра на простом примере решения линейного уравнения с одним неизвестны.
Задача 16. Решить уравнение 10· x - 10 / x = 15.
Решение. Для искомого значение параметра – x выберем ячейку A3. Введем в эту ячейку любое число, лежащее в области определения функции (в нашем примере это число не может быть равно нулю). Пусть это будет 3. Это значение будет использовано в качестве начального. В ячейку, например, B3 в соответствии с приведенным уравнением введем формулу =10*A3-10/A3. В результате серии расчетов по данной формуле будет отобрано искомое значение параметра. Теперь в меню Сервис, выбрав команду Подбор параметра, запустим функцию поиска параметра (рис.11, а). Введем параметры поиска:
· В поле Установить в ячейке введем абсолютную ссылку на ячейку $В$3, содержащую формулу.
· В поле Значение введем искомый результат 15.
· В поле Изменяя значение ячейки введем ссылку на ячейку А3, содержащую подбираемое значение, и нажмем <OK>.
По окончании работы функции Подбор параметра на экране появится окно Результат подбора параметра, в котором будут отображены результаты поиска. Найденный параметр 2,000025 появится в ячейке А3, которая была для него зарезервирована.
Обратите внимание на тот факт, что в нашем примере уравнение имеет два решения, а параметр подобран только один. Это происходит потому, что параметр изменяется только до тех пор, пока требуемое значение не будет возвращено. Первый найденный таким образом аргумент и возвращается к нам в качестве результата поиска. Если в качестве начального значения в нашем примере указать -3, тогда будет найдено второе решение уравнения: -0,5.
а) б)
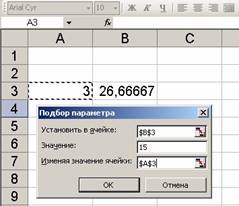
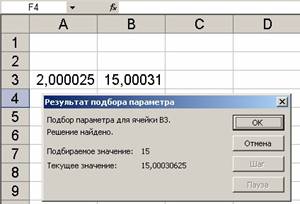
Рис.11. Решение уравнения: а- ввод данных, б- результат решения
Задача 17. Решить уравнения
1. 5х/ 9- 8= 74- 7x/ 12 2. (2x+ 2)/ 0.5= 6x
3. 0,5 (2x- 1)+x/ 3= 1/6 4. 7 (4x- 6)+ 3 (7- 8x)= 1
Систему линейных уравнений можно решать различными способами: подстановки, сложения и вычитания уравнений, с использованием матриц. Рассмотрим способ решения канонической системы линейных уравнений (3) с использованием матриц.
a1 x + a2 y + b1= 0
(3) a3 x + a4 y + b2 =0
Известно, что система линейных уравнений в матричном представлении записывается в виде:
A X = B,
где А – матрица коэффициентов, X– вектор - столбец неизвестных, В – вектор-столбец свободных членов. Решение такой системы записывается в виде
где A-1 –матрица, обратная по отношению к А. Это вытекает из того, что при решении матричных уравнений при X должна остаться единичная матрица Е. Умножая слева обе части уравнения АХ = В на А-1, получаем решение линейной системы уравнений.
Задача 18. Решить систему линейных уравнений
2x + y = 3
4x + 5y = 2
Решение. Для данной системы линейных уравнений значения соответствующих матрицы и вектора-столбца имеют вид:
⎛ 2 1⎞ ⎛ 3⎞
A = ⎜⎜⎝ 4 5⎟⎟⎠ B = ⎜⎜⎝ 2⎟⎟⎠
Для решения задачи выполним действия:
· Выделим блок ячеек, например, А2:В3 и запишем в него элементы матрицы А.
· Выделим блок ячеек, например, С2:С3 и запишем в него элементы матрицы В.
· Выделим блок ячеек, например, D2:D3 для помещения результата решения системы уравнений.
· в ячейку D2 введем формулу = МУМНОЖ(МОБР( А2:В3);С2:С3).
Библиотека Excel в разделе математических функций содержит функции для выполнения операций над матрицами. В частности, это функции:
|
Функция |
Выполняемое действие |
|
МОБР (параметр) |
обращение матрицы |
|
МОПР (параметр) |
вычисление определителя матрицы |
|
МУМНОЖ (список параметров) |
умножение матриц |
Параметрами данных функций могут быть адресные ссылки на массивы, содержащие значения матриц или имена диапазонов и выражения. Например, МОБР (А1: B2) или МОПР (матрица_1).
· Укажем Excel, что выполняется операция над массивами, для этого нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter>, в ячейках D2 и D3 будет получен результат х = 2,16667; y= - 1,33333.
Задача 19. Решите систему линейных уравнений
1. 3x + 2y = 8 2. 5x + y = 7 3. 5x + 4y = 22 4. 3x - 4y = -17
5x + y = 11 4x + 3y = -1 3x + y = 9 5x + 3y = - 9
Многие проблемы прогнозирования, проектирования и производства сводятся к широкому классу задач оптимизации. Такими задачами являются, например: максимизация выпуска товаров при ограничениях на сырье для производства этих товаров; составление штатного расписания для достижения наилучших результатов при наименьших расходах; минимизация затрат на транспортировку товаров; достижение заданного качества сплава; определение размеров некоторой емкости с учетом стоимости материала для достижения максимального объема; различные задачи, в которые входят случайные величины, и другие задачи оптимального распределения ресурсов и оптимального проектирования.
Решение задач такого вида может быть осуществлено EXCEL с помощью инструмента Поиск решения, который расположен в меню Сервис. Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи надо начинать с построения соответствующей модели. Познакомимся с этими командами на примере.
Задача 20. Предположим, что мы решили производить два вида объективов А и В. Объектив вида А состоит из 3-х линзовых компонентов, вид В – из 4-х . За неделю можно изготовить не более 1800 линз. На сборку объектива вида А требуется – 15 минут, вида В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько объективов А и В надо изготовить, чтобы получить максимальную прибыль, если объектив вида А стоит 3500 рублей, вида В – 4800 рублей.
Решение. Для решения этой задачи необходимо составить и заполнить таблицу в соответствии с рис. 12:
· Переименуем ячейку В2 в x, количество объективов вида А.
· Аналогично переименуем ячейку В3 в y.
· Целевую функцию Прибыль = 3500*x+4800*y введем в ячейку B5.
· Затраты на комплектацию равны =3*x+4*y введем в ячейку B7. · Затраты по времени равны =0,25*x+0,5*y введем в ячейку B8.
|
|
А |
|
В |
|
1 |
Наименование |
|
Формулы |
|
2 |
А |
|
“x” |
|
3 |
В |
|
“y” |
|
4 |
|
|
|
|
5 |
Прибыль |
|
= 3500x+ 4800y |
|
6 |
|
|
|
|
7 |
Затраты комплектацию |
на |
= 3x+ 4y |
|
8 |
Затраты по времени |
= 0,25x+ 0,5y |
|
|
9 |
|
|
|
Рис.12. Заполнение таблицы исходными данными
· Выделим ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним ячейки этого окна в соответствии с рис.13.
· Нажмем <Выполнить>; если все сделано правильно, то решение будет таким, как указано ниже.
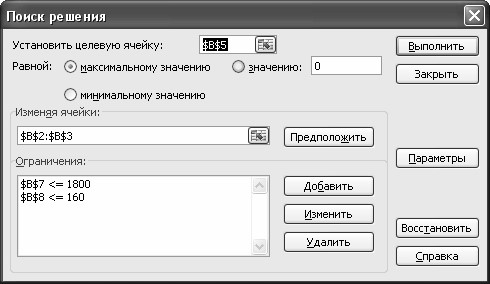
Рис.13. Пример заполнения окна Поиск решения
|
|
А |
|
В |
|
1 |
Наименование |
|
Формулы |
|
2 |
А |
|
520 |
|
3 |
В |
|
60 |
|
4 |
|
|
|
|
5 |
Прибыль |
|
210800 |
|
6 |
|
|
|
|
7 |
Затраты комплектацию |
на |
1800 |
|
8 |
Затраты по времени |
160 |
|
Рис.14. Вид таблицы результатов решения с применением команды Поиск решения
Из решения видно, что оптимальный план выпуска объективов составляет 520 штук вида А и 60 штук вида В. При этом максимальная прибыль составит 2108000 рублей.
Задача 21. Штат научно-исследовательской лаборатории (НИЛ) должен состоять из: 5…7 лаборантов, 8…10 инженеров, 11 младших научных сотрудников (м.н.с.), 3 старших научных сотрудников (с.н.с.), 2 ведущих научных сотрудников, и заведующего НИЛ. Общий месячный фонд зарплаты составляет 400 т.руб. Необходимо определить, какими должны быть оклады сотрудников НИЛ при условии, что оклад лаборанта не должен быть меньше прожиточного минимума 6 т.руб.
Решение. В качестве математической модели этой задачи возьмем линейное уравнение:
N1· A1· C+N2· (A2· C+ B2)+... +N6· (A6· C+ B6) = 400 000
В основу данной модели взят оклад лаборанта С, а остальные оклады будем вычислять, исходя из него: во сколько раз или на сколько больше оклада лаборанта: Ai· С+ Вi, где Аi и Вi - коэффициенты, которые для каждой должности определяются выбранными условиями:
· Инженер получает в 1,8 раза и на 600 руб. больше лаборанта (А2= 1,8; В2=600).
· М.н.с. - в 1,8 раза больше лаборанта и на 1100 руб. больше инженера
(А3= 1,5; В3= 1700).
· С.н.с. - в 3,5 раза больше лаборанта (А4= 3,5; B4= 0).
· Ведущий научный сотрудник - в 3,2 раза больше лаборанта, на 3200 руб. больше с.н.с. (А5= 3,2; В5= 5000).
· Заведующий НИЛ в 5 раз больше лаборанта (А6= 5; В6= 0).
В приведенной выше зависимости Ni число сотрудников одной должности. Неизвестными данного уравнения являются число лаборантов (N1),число инженеров (N2) и оклад лаборанта (С).
Введем исходные данные в рабочий лист электронной таблицы, как показано ниже (рис.15). В ячейки столбцов B и C запишем значения коэффициентов А и В. В ячейки E3:E4 запишем любые числа из указанного в условии задачи диапазона. В ячейки D3, F3 и F9 запишем расчетные формулы, соответственно: =$G$7*B3+C3; = D3*E3 и =СУММ(F3:F8). Затем в меню Сервис активизируем команду Поиск решения.
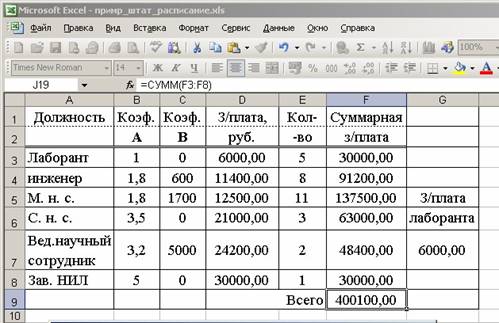
Рис.15. Вид решение задачи № 21
В поле Установить целевую ячейку: укажем ячейку F9, содержащую целевую функцию. Поскольку общий фонд зарплаты указан точно, то активизируем поле “Значению:”, в котором запишем 40000.
Используя кнопку Добавить, опишем ограничения задачи. Окончательно окно Поиска решения будет выглядеть так:
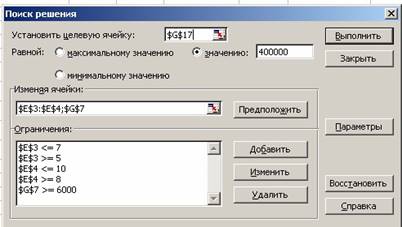
Рис.16. Вид заполненного окна Поиск решения
Щелкнем на кнопке Выполнить. Получим решение, которое приведено на рис. 15.
Задача 22. Спроектировать емкость - параллепипед с объемом V= a· b· h = 3000 (длина, ширина, высота). Емкость должна иметь минимальную площадь стенок S = ab+ab+bh+bh+ah+ah.
Задача 23. Участок имеет площадь S= а· b= 800 м2. При какой длине (а) и ширине (b) периметр будет минимальным.
Задача 24. Из квадратного листа со стороной А делается коробка (рис.17). Для этого по углам листа вырезаются квадраты со стороной х. Определить сторону вырезаемого квадрата, при условии, что коробка имела бы максимальный объем. Проведите решения для разных исходных данных: А= 60 см, А=100 см, А=110 см.
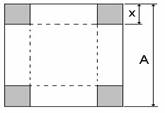
Рис.17. Схема разметки листа для изготовления коробки
Задача 25. Где должна располагаться точка С - х, для того, чтобы сумма отрезков АС и СВ была минимальной (рис.18)?
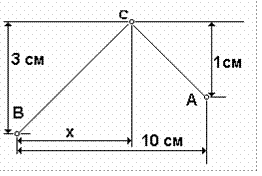
Рис.18. Схема и исходные данные для задачи № 25
Существует две основные группы статистических задач: организация и проведение статистического наблюдения; обработка и анализ статистических данных. Входящие в состав статистического наблюдения данные должны быть максимально полными, абсолютно достоверными и точными, чтобы получить массовые и надёжные материалы о различных технических явлениях. Собранные в процессе статистического наблюдения данные должны быть обработаны так, чтобы получился точный и обстоятельный ответ на все вопросы, поставленные целью исследования. Для решения указанных задач применяются методы теории вероятности и математической статистики.
Самая простая статистическая задача при анализе данных, содержащихся в некотором массиве, заключается в поиске его элементов с максимальным, минимальным и средним значениями. В Excel определены следующие быстрые функции для нахождения данных элементов массива:
· МАКС(а;b;…) — возвращает наибольший элемент;
· МИН(а;b;…) — возвращает минимальный элемент из списка; · СРЗНАЧ(а;b;…) — возвращает средний элемент из списка; · МАКС(а;b;…)- МИН(а;b;…) - размах элементов из списка.
Задача 26. Определить максимальное, минимальное и среднее значения чисел, указанных в ниже приведенной таблице
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
Решение. Сначала заполним данными из таблицы блок ячеек Excel A1:G7.
Для определения максимального значения кнопкой < fx > вызываем окно Мастер функций, в котором выбираем Категория - Статистические, Выберите функцию – МАКС. В открывшемся окне Аргументы функции в строке Число записываем блок A1:G7 и нажимаем < ОК >. В заранее выбранной ячейке получаем максимальное значение элемента – 49. Аналогично: минимальное значение элемента - 1, среднее значение элемента -25.
Задача 27. Определить максимальное, минимальное значение и размах чисел, указанных в ниже приведенной таблице
|
35 |
1 |
6 |
26 |
19 |
24 |
|
3 |
32 |
7 |
21 |
23 |
25 |
|
31 |
9 |
2 |
22 |
27 |
20 |
|
8 |
28 |
33 |
17 |
10 |
15 |
|
30 |
5 |
34 |
12 |
14 |
16 |
|
4 |
36 |
29 |
13 |
18 |
11 |
К более сложным задачам относятся задачи, где необходимо определить набор свойств полученных данных: статистические характеристики, критерии согласия и ряд др. Вместе с этим построить графическую интерпретацию полученных данных.
Задача. 28. В таблице приведены результаты измерения диаметров
|
26 |
30 |
29 |
28 |
25 |
28 |
30 |
29 |
27 |
25 |
28 |
27 |
32 |
31 |
28 |
|
29 |
24 |
28 |
28 |
31 |
29 |
24 |
29 |
30 |
25 |
31 |
30 |
23 |
29 |
27 |
валиков. Определить основные статистические характеристики выборки. Построить статистические ряды, график рассеяния значений диаметров.
Решение. Для решения этой задачи выполним последовательность действии:
· Определяем минимум, максимум, объем выборки, количество и длину интервалов.
Для этого воспользуемся встроенными в Excel статистическими функциями аналогично предыдущей задачи, занесем соответствующие формулы в ячейки B5:B7. Количество интервалов N вычисляем в ячейке
B8 по формуле Стерджесса, символьный вид которой
=ОКРУГЛ(1+3,322LOG10(B7);0). Количество интервалов, естественно, округляется до целого. Длину интервала h вычисляем в ячейке B9 по формуле =(B6- B5)/ B8. Результат показан на рис. 19.
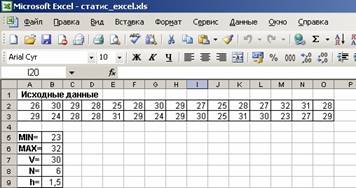
Рис.19. Определение статистических характеристик массива A2: O3
· Строим вариационный ряд.
Для этого расположим элементы выборки по возрастанию с помощью функций НАИМЕНЬШИЙ (массив; n) и СТОЛБЕЦ(). Записываем в ячейку А12 формулу = НАИМЕНЬШИЙ(2:3;СТОЛБЕЦ()) и перетаскиваем ее вправо. В результате в ячейке А12 оказывается минимальный элемент выборки – 23, В12 – 24 и т.д.
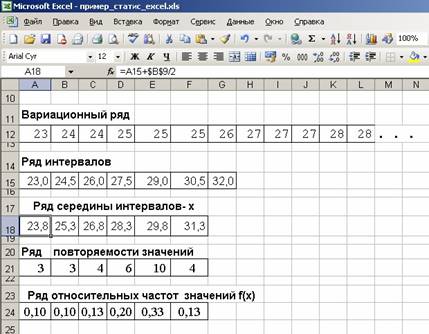
Рис. 20. Построение статистических рядов
Ряд интервалов начинается с минимального значения выборки. Поэтому помещаем в ячейку A15 формулу =А12. Остальные точки отстоят друг от друга на длину интервала (ячейка В9). Затем заносим в B15 формулу =A15+$В$9 и копируем В15 вправо.
Ряд середины интервалов. Середина первого интервала равна левому концу интервала (A12) плюс половина его длины (В9). Заносим в A18 формулу =A15+ $B$9/2 и копируем ее вправо.
Ряд повторяемости значений. Число элементов выборки, принадлежащих интервалу [a; b), равно числу элементов, меньших b минус число элементов, меньших a.
Для их подсчета воспользуемся функцией СЧЁТЕСЛИ(массив; критерий). Заносим в ячейку A21 формулу =СЧЁТЕСЛИ(А2:О3 "<"&B15) – СЧЁТЕСЛИ(А2:О3; "<"&A15) и копируем ее вправо. Знак & обозначает объединение двух значений: объединяем текст “<” и адрес конкретной ячейки “B15”.
Ряд относительных частот значений. Делим элементы ряда
повторяемости значений на объем выборки. Для этого набираем в в ячейке A24 формулу =A21/$B$7 и копируем ее вправо. Результаты построения статистических рядов показаны на рис.20.
· Строим гистограмму и полигон относительных частот выборки (рис. 22).
Для формирования исходных данных выделим блоком A24:F24 ряд относительных частот. Вызовем Мастер диаграмм. Откроем закладку Нестандартные, Тип: График | гистограмма, нажмем <Далее>. В появившемся новом окне откроем закладку Ряд, нажмем <Добавить>. Справа от Значение: введем данные из блока A24:F24. Для Подписи оси Х: введем данные из блока A18:F18. В результате получится картинка (рис.21). Нажмем <Далее>. В закладке Заголовки наберем Название диаграммы: Гистограмма и полигон рассеяния частот значений диаметров f(x).Теперь можно нажать <Готово>. После этого
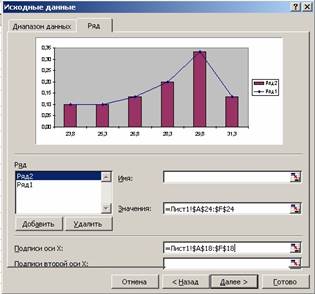
Рис.21. Вид окна при построении гистограммы и полигона можно редактировать диаграмму, в частности, убрать промежутки между
столбиками гистограммы (рис.22). (См. раздел Создание диаграмм).
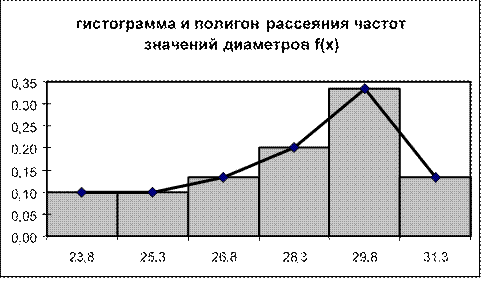
Рис. 22. Вид гистограммы и полигона рассеяния
Задача 29. Дана выборка: 13, 1, 15, 12, 11, 14, 2, 5, 6, 17, 25, 3, 4, 8, 10,15, 3, 10, 8, 9. Построить вариационный ряд, определить стандартные характеристики рассеяния, построить полигон рассеяния.
Задача 30. Для оценки надежности партии приборов были проведены натурные испытания. Результаты испытания оценивались в дихотомической шкале: за безотказную работу начисляется один балл, за отказ в процессе испытаний – нуль баллов (см. таб.). Провести статистическую обработку
|
|
|
№ (вид) Отказа |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
4 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
5 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
6 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
7 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
8 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
10 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
данных, как по номерам приборов, так и по видам отказов. Рассчитать стандартные статистические характеристики, построить гистограмму рассеивания данных испытаний.
Здесь решается вопрос: отражают ли наблюдаемые данные объективно существующую реальность. Указанный вопрос решается статистической оценкой параметров распределения и проверкой соответствующих статистических гипотез.
Параметр распределения - среднее значение, получаемое по выборочным данным, обычно не совпадает с генеральным средним (математическим ожиданием). В связи с этим возникает вопрос: можно ли по результатам выборочной оценки судить о свойствах всей генеральной совокупности? Ответить на этот вопрос позволяют интервальные оценки, которые позволяют установить точность и надежность полученных оценок.
Пусть найденная по данным выборки статистическая характеристика M ′ служит оценкой неизвестного параметра M. Тогда можно записать
│M – M′│< δ,
где δ - характеризует точность оценки.
Статистические методы не позволяют категорически утверждать, что оценка M′ удовлетворяет неравенству │M – M′│< δ; можно лишь говорить о вероятности f, с которой это неравенство осуществляется. Надежностью (доверительной вероятностью) оценки M по M′ называют вероятность f = 0,95; 0,99; 0,999, с которой осуществляется неравенство │M – M′│< δ.
Доверительным интервалом называется случайный интервал (M′ - δ; M′ + δ), в пределах которого с вероятностью f находится неизвестный оцениваемый параметр. Число f называется коэффициентом доверия. Это значение задают заранее. Число p=(1- f) называется уровнем значимости и показывает, с какой вероятностью заключение о надежности оценки ошибочно.
С учетом возможных значений f, p= 0,05; 0,01; 0,001.Очевидно, что чем меньше p, тем точнее оценка.
Доверительный интервал для математического ожидания нормально распределенного признака с известным средним квадратическим отклонением находят по формуле
S S
M −
tn.p ![]() ;M + tn.p.
;M + tn.p. ![]()
где М — среднее значение, S — среднее квадратическое отклонение, t n. p. — табличное значение распределения Стьюдента с числом степеней свободы (n- 1) и доверительной вероятностью р, n — количество элементов в выборке. При необходимости коэффициент Стьюдента можно определить, воспользовавшись статистической функцией Excel
СТЬЮДРАСПОБР(надежность; число степеней свободы).
Задача 31. Найти границы 95%-ного доверительного интервала для среднего значения, если у 25 аккумуляторов среднее время разряда в режиме ожидания составило 140 часов, а стандартное отклонение — 2,5 часа.
Решение. Для определения границ доверительного интервала откроем новое окно Exce1.
· Установим табличный курсор в ячейку А2.
· Вызовем окно Мастер функций, нажмем < Вставка функции > (fx). · В появившемся окне выберем категорию Статистические и функцию ДОВЕРИТ, после чего нажмем <ОК>.
· В рабочие поля появившегося диалогового окна Аргументы функции с клавиатуры введем условия задачи: уровень значимости (Альфа) – 0,05; среднее квадратическое отклонение (Станд_откл) – 2,5; количество элементов в выборке (Размер) –25 (рис. 6.11). Нажмем <ОК>.
· В ячейке А2 появится полуширина 95%-ного доверительного интервала для среднего значения выборки – 0,98.
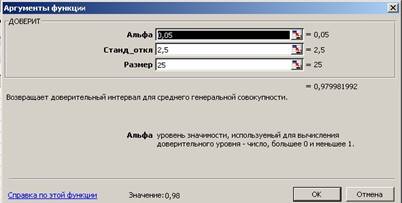
Рис.21. Вид заполненного окна функции ДОВЕРИТ
На основании проделанного решения можно с 95%-ным уровнем надежности утверждать, что средняя продолжительность разряда аккумулятора составляет 140 ± 0,98 часа или от 139,02 до 140,98 часа.
Задача 32. Имеются результаты измерения диаметров отверстий: 13, 15, 17, 19, 22, 25, 19, 20, 25. Определить среднее значение результатов и границы 99%-ного доверительного интервала для среднего значения.
Задача 33. Исследовалось время безотказной работы 50 лазерных принтеров. Из априорных наблюдений известно, что среднее квадратическое отклонение времени безотказной работы 16 час. По результатам исследований получено среднее время безотказной работы 1000 час. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.
Задача 34. Для определения средней массы деталей были взвешены 100 штук и результаты сведены в таблицу:
|
Масса, кг |
23-25 |
25-27 |
27-29 |
29-31 |
31-33 |
33-35 |
35-37 |
|
Число дет., шт |
3 |
10 |
6 |
16 |
15 |
30 |
20 |
Найти:
1. Величины, которые следует принять за среднюю массу деталей и среднее квадратическое отклонение.
2. Доверительный интервал, в котором с вероятностью 0,95 заключена средняя масса деталей.
Доверительный интервал для среднего квадратического отклонения нормального распределения. Математические формулы для вычисления соответственно левого и правого концов доверительного интервала:
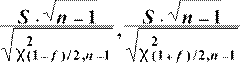
где S – среднее квадратическое отклонение, χ2– табличные значения распределения хи-квадрат при f - коэффициенте доверия и n – количестве элементов в выборке.
Чтобы найти значение статистической функцией χ2, необходимо воспользоваться электронным аналогом функции Excel –
ХИ2ОБР(аргумент1;аргумент2), где аргумент 1 – значение вероятности; аргумент 2 – число степеней свободы χ2 распределения.
Задача 35. Результат измерения ширины деталей одного типа — случайная величина, распределенная по нормальному закону. Случайным образом выбраны 20 деталей и произведены замеры. Исправленная выборочная дисперсия измерений оказалась равной 22,5. Найти доверительный интервал для неизвестного среднего квадратического отклонения измеренных значений ширины деталей с надежностью 98%.
Решение. Для определения границ доверительного интервала откроем новое окно Exce1.
· Запишем в ячейки таблицы исходные данные: дисперсия S2 в ячейку D22, число измеренных деталей n - D24, коэффициент доверия f - D23 .
· По числу степеней свободы, равному 19, и по вероятности (1 – 0,98)/2 = 0,01 находим χ22 = 36,2. Аналогичным образом при вероятности (1+ 0,98)/2 = 0,99 получаем χ12 = 7,63. Используя, выше приведенную формулу, получаем искомый доверительный интервал:
(3,44; 7,49). Соответствующие формулы Excel:
=(D22*(D24-1)/ХИ2ОБР((1-D23)/2;D24-1))^0,5
=(D22*(D24-1)/ХИ2ОБР((1+D23)/2;D24-1))^0,5
Задача 36. Найти доверительный интервал для σ при условии: 1) S = 1,3; заданная надежности f = 0,95; n= 20 и n= 42. Сравните результаты.
2) n= 25, S= 0,8; заданная надежности f = 0,90.
Задача 37. Определение коэффициента пропускания для различных образцов одной партии стекла марки ОС17 дало следующие результаты: 0,21; 0,17; 0,18; 0,13; 0,19; 0,14; 0,20 и 0,18. Считая, что полученные значения распределены по нормальному закону, требуется определить доверительный интервал для σ при значениях доверительной вероятности
0,9 и 0,95.
Статистическая проверка статистических гипотез необходима для решения вопроса, отражают ли наблюдаемые данные объективно существующую реальность. Указанный вопрос решается проверкой соответствующих статистических гипотез. Статистическая гипотеза – это предположение о виде или отдельных параметрах распределения вероятностей, которое подлежит проверке на имеющихся данных. Проверка статистических гипотез – это процесс формирования решения о возможности принять или отвергнуть утверждение (гипотезу), основанный на информации, полученной из анализа выборки. Методы проверки гипотез называются критериями. В большинстве случаев рассматривают так называемую нулевую гипотезу (Н0), состоящую в том, что все события произошли случайно.
Наиболее часто проверяется предположение о нормальном распределении вероятностей, поскольку большинство статистических
процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности. Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют критерии согласия. Критериями согласия называют статистические критерии, предназначенные для проверки согласия опытных данных и теоретической модели.
Среди критериев согласия большое распространение получил непараметрический критерий χ2 (хи-квадрат). Он основан на сравнении эмпирических частот интервалов группировки с теоретическими частотами, рассчитанными по формулам нормального распределения. Уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных можно говорить только о том, что данные не противоречат нормальному закону.
Использование критерия согласия хи-квадрат. Для применения критерия желательно, чтобы объем выборки n ≥ 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находилось не менее 5 наблюдений (частот).
Сравниваться должны именно абсолютные частоты, а не относительные
(частости).
Критерий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отвергнуть с определенной вероятностью (уровнем значимости).
В таблицах Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ вычисляет вероятность совпадения наблюдаемых значений и теоретических значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соответствия экспериментальных данных нормальному закону распределения. Функция имеет аргументы:
ХИ2ТЕСТ(фактический_интервал;ожидаемый_интервал). Здесь: фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями; ожидаемый_интервал — это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.
Задача 38. Построить эмпирическое распределение числовой последовательности: 64, 57, 63, 62, 58, 61, 63, 60, 60, 61, 65, 62, 62, 60, 64, 61, 59, 59, 63, 61, 62, 58, 58, 63, 61, 59, 62, 60, 60, 58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65. Проверить соответствие приведенных данных нормальному закону распределения.
Решение. Выполним следующую последовательность действий:
· Заполним блок А2:Е12 заданной числовой последовательностью.
· Oпределим V=65, Max =65, Min =57, используя статистические функции
Excel .
· Выберем ширину интервала 1. Тогда при крайних значениях 57 и 65 получится 9 интервалов.
· Заполним блок G2:G10 граничными значениями интервалов (57, 58, 59, 60, 61, 62, 63, 64, 65).
· Заполним столбец Н значениями абсолютных частот.
Для этого выделим блок ячеек Н2:Н10, вызовем Мастер функций нажатием <fx>. В появившемся диалоговом окне выберем статистические функцию ЧАСТОТА, после чего нажмем <ОК>. В рабочее поле Массив_ данных введем данные числовой последовательности А2:Е12. В рабочее поле Массив_интервалов введем диапазон интервалов G2:G10. Последовательно нажмем комбинацию клавиш Ctrl+Shift+ Enter. После нажатии < ОК > в блоке ячеек Н2:Н10 появится массив абсолютных частот (см. рис. 22)
· Убедимся, что полученный массив частот соответствует исходным данным.
Для этого проведем суммирование частот в ячейке Н11. Табличный курсор установим в ячейку Н11, а на панели инструментов Стандартная нажмем < Автосумма >. В ячейке Н11 должно появится 55 - количество значений в числовой последовательности.
· Найдем теоретические частоты нормального распределения. Cначала найдем среднее значение Xср. и стандартное отклонение выборки S.
Для этого используем встроенные функции Excel СРЗНАЧ и СТАНДОТКЛОН. Затем с помощью функции НОРМРАСП найдем теоретические частоты. Запишем в ячейку I2 формулу =$H$14*НОРМРАСП(G2;$H$17;$H$18). Далее протягиванием скопируем содержимое ячейки I2 в диапазон ячеек I2:I10. Результаты вычислений представлены на рис. 22.
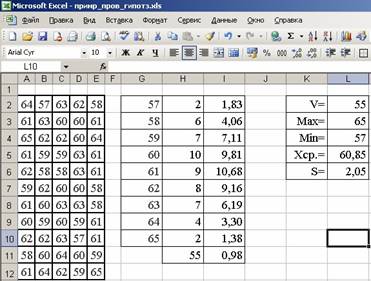
Рис.22. Результаты вычисления теоретических частот и проверки статистической гипотезы
· С помощью функции ХИ2ТЕСТ определим соответствие данных нормальному закону распределения.
Для этого установим табличный курсор в свободную ячейку I11. Вызываем окно Мастер функций, где выбираем функцию ХИ2ТЕСТ. В диалоговое окно ХИ2ТЕСТ в рабочие поля введем фактические Н2:Н10 и ожидаемые I2:I10 диапазоны частот (рис. 22). Нажмем <ОК >. В ячейке I11 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения – 0,98.
Задача 39. Проведено измерение толщины образцов стеклянной пластины:
21, 21, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26, 27, 27. Найдите соответствие экспериментальных данных нормальному закону распределения.
Задача 40. Создать последовательность, состоящую из 60 действительных случайных чисел, распределенных в диапазоне от 30 до 70. Проверить гипотезу о нормальном распределении, используя критерий согласия Пирсона, при уровне значимости p= 0,05.
Диаграмма – это способ графического представлении информации. Таблицы Excel имеют большие возможности для построения диаграмм и их модификации. Диаграммы могут создаваться как на листе таблицы (внедренные диаграммы), так и на отдельном листе диаграммы (отдельные диаграммы). В обоих случаях необходимо сначала создать таблицу значений, затем выделить данные, которые требуется представить в графическом виде, включая заголовки строк и столбцов. Затем перейти к инструменту построения – Мастер диаграмм.
Задача 41. Построить диаграммы годового выпуска подшипников по данным таблицы, показанной на рис. 24.
Решение. Решение предполагает последовательность действий:
· Выделим c помощью мышки блок ячеек B1:M4.
· Вызовем диалоговое окно Мастер диаграмм, сделать
это можно, выбрав в меню Вставка, Диаграмма, либо кнопка ![]() , откроется диалоговое окно Мастер
диаграмм (Рис.23).
, откроется диалоговое окно Мастер
диаграмм (Рис.23).
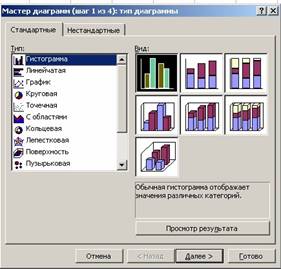
Рис.23. Вид окна Мастер диаграмм
· Выберем Тип диаграммы. Тип зависит от того, что представляем: для динамических процессов подойдут типы диаграмм Гистограмма, Линейчатая, График, для вычленения долей – Круговая, Кольцевая, Лепестковая. Наша задача изобразить процесс, поэтому выбираем тип диаграммы График с маркерами, отмечающими точки с данными.
· Нажимаем <Далее>, Еxcel показала картинку, как предварительно выглядит график.
· Откроем закладку Ряд, каждый ряд значений –I, II, сумма порождают свой график.
· Занесем в поля Имя и Значения адреса ячеек, где они записаны, при этом поля Имя и Значения подчинены выделенному Ряду.
· Удалим Ряд 3 – «сумма», как не нужный для иллюстрации процесса: выделим Ряд 3, затем < Удалить >;
· Нажимаем < Далее >, появляется набор закладок : Легенда – помогает разместить пояснения к диаграмме, Заголовки – записываются название диаграммы и осей, названия остальных закладок вполне адекватны их действиям.
· Нажимаем <Далее>, открывается окно Размещение диаграммы, поместим ее на имеющемся листе Работа завершена, см. рис. 24:
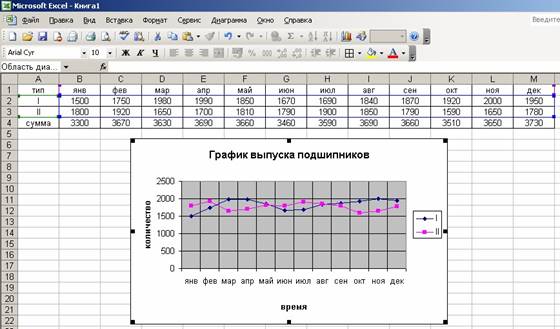
Рис. 24. Результат построения диаграммы (Задача 41)
Задача 42. Построить совмещенные графики функции y=f(x) на отрезке [a;b] с шагом h= c. Исходные данные приведены в табличной форме:
|
Вариант |
Функция 1 |
Функция 2 |
Изменения Х |
|
1 |
У1= -2/х |
У2=4х |
[0,5; 5,0], h=0,5 |
|
2 |
У1 = 2х |
У2=(1/2)х |
[0,5; 5,0] h=0,5 |
|
3 |
У1=lnх |
У2 =log10х |
[0,5; 5,0] h=0,5 |
Круговые диаграммы используются для отображения только одного ряда данных и показывают отношение величин элементов, образующих ряд, к величине суммы элементов. Этот тип диаграммы целесообразно использовать, когда необходимо показать составные части целого. Круговая диаграмма выводит данные как сегменты круга. Excel использует первую строку (столбец) выделенных данных для определения надписей для каждого сегмента, а вторая строка (столбец) определяет собственно значения данных.
Задача 43. Создать круговую диаграмму по средним показателям объема, занимаемого механическими, электронными и оптическими деталями в фотокамере.
Решение. Выполним последовательность действий:
· Выделим диапазоны данных, содержащие показатели В2:B4 (рис.25).
· Выберем в меню Вставка команду Диаграмма;
· В открывшемся окне Мастер диаграмм выберем Круговая, Объемный вариант.
· В закладке Подписи данных поставим флажки (∨) напротив команд имена категорий и значения.
· В закладке Заголовки напишем Название диаграммы и нажмем <Готово>.

Рис. 25. Построение круговой диаграммы
Задача 44.
1. Используя данные таблицы (таб.5), постройте три отдельные диаграммы:
· Круговую диаграмму, отражающую структуру продаж оптических приборов за первый квартал. Отобразите долю каждого прибора в %;
· Круговую диаграмму, отражающую структуру продаж оптических приборов за второй квартал. Отобразите долю каждого прибора в %;
· Гистограмму, отражающую сравнительный объем продаж оптических приборов.
Объем продаж
Таблица 5.
|
Наименование |
I квартал |
II квартал |
|
Бинокль |
100 |
35 |
|
Микроскоп |
70 |
100 |
|
Визирная труба |
40 |
65 |
|
Лазерный дальномер |
55 |
120 |
|
Лазерный нивелир |
25 |
150 |
2. Используя данные, приведённые в таблице (таб.6 ), вычислите прирост выпуска продукции черной металлургии за 5 лет. Постройте круговую плоскую диаграмму, отражающую структуру прироста. Производство продукции
Таблица 6.
|
Наименование |
n |
n+ 5 |
Прирост |
|
Кокс, тыс. т. |
601 |
1060 |
|
|
Сталь, тыс. т |
590 |
965 |
|
|
Чугун, тыс. т |
640 |
815 |
|
|
Прокат, тыс. т |
670 |
919 |
|
Трехмерные графики удобно использовать при иллюстрации функций двух переменных. Общее уравнение функции имеет вид z = f(x, y), где x и y — аргументы, z — значение функции.
Задача 45. Построить график функции : f (x, y) = x2 + y2, где x∈[–5, 5], y ∈[–9, 9]. Шаг изменения значений x и y, равен: t= 0,5.
Решение. Для построения трехмерного графика выполним последовательность действий:
· На рабочем листе Excel (см. рис. 26) зададим пошагово значения аргументов в виде строки B1:V1 для x и столбца A2:A38 для y (выбор величины шага t определяется исходя из требуемой “подробности” построения графика).
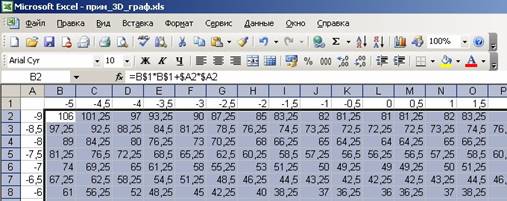
Рис. 26. Таблица формирования массива данных (часть)
· Введем в ячейку B2 формулу функции =B$1*B$1+$A2*$A2.
При заполнении интервала по горизонтали формулы во всех ячейках должны ссылаться на соответствующую ячейку верхнего ряда, следовательно, она должна иметь абсолютную адресацию по номеру строки, а по номеру столбца – относительную адресацию. В нашем случае адресация выглядит так: B$1. По вертикали, наоборот: абсолютным должен быть номер столбца, а номер строки – относительным, т.е. адрес имеет вид $A2. Чтобы не использовать дополнительных функций, в квадрат будем возводить просто умножением.
· Этой формулой заполним весь блок от B2 до V38. В результате имеем массив данных для построения графика (рис. 26)
· Вызываем Мастер диаграмм, тип диаграммы – Поверхность, вид – Поверхность, изменение по двум измерениям.
Мастер диаграмм сам выберет участок таблицы, из которого надо брать данные, и построит диаграмму (рис. 27). Далее можно усовершенствовать оформление диаграммы. Например, получить более тонкие полосы. Для этого надо выбрать вертикальную ось, по терминологии Excel –ось значений, и задать меньшую цену основных делений – 4…5.
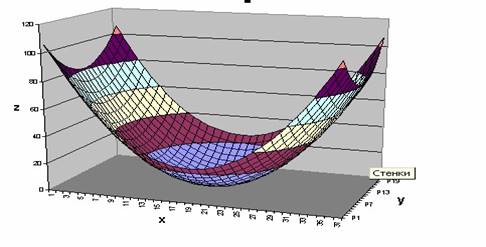
Рис. 27. Трехмерный график функции z = f(x, y),
Задача 45. Построить графики функции:
1. z= x2 – y2
2. z = sin(x + y) / (x + y)
Область значений x, y и шаг изменения значений t подберите самостоятельно.
3. x2 + y2+r2 = 16, где x (y) ∈ [–5, 5], t=0,5
4. z = ( x/ a)2 - (y/ b)2, где a=4, b=5, x (y) ∈ [–5, 5], t=0,5
5. z = ( x/ a)2 + (y/ b)2, где a=1, b=1, x (y) ∈ [–5, 5], t=0,5
Для редактирования построенной диаграммы необходимо дважды по ней щелкнуть. Если выполнить щелчок по элементу диаграммы: ось, график, название и т.п., то попадаете в режим редактирования данного элемента, при этом будет открыто соответствующее окно. Кроме того можно радикально изменить сам тип построенной диаграммы. Инструмент для этого находится в меню Диаграмма. Это меню Excel предлагает после выделения Области диаграммы. В данном меню расположен ряд команд. Тип диаграммы позволяет изменить тип построенной диаграммы, например, График с маркерами на График изменения процесса. Исходные данные, команда дает возможность откорректировать данные (численные значения, размещение в ячейках и другие). Добавить данные, команда позволяет, изменит диаграмму за счет дополнительных данных, размещенных в новых диапазонах ячеек.
Отдельно остановимся на команде Добавить линию тренда. Это один из наиболее простых технических инструментов, используемых в графическом анализе. Линия тренда – графическое представление направления изменения данных в ряде данных (тенденция зависимости). Линии тренда используются при прогнозировании, например, при регрессионном анализе. Регрессионный анализ - вид статистического анализа, используемый для прогнозирования. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения переменной из нескольких уже известных значений.
Линии тренда могут быть построены на всех двухмерных диаграммах без накопления: гистограмме, линейчатой диаграмме, графике, точечной диаграмме, а также пузырьковых диаграммах. Нельзя дополнить линиями тренда ряды данных на объемных диаграммах, нормированных диаграммах, лепестковых диаграммах, круговых и кольцевых диаграммах. При замене типа диаграммы на один из вышеперечисленных, например, изменении типа диаграммы на объемную диаграмму или изменении представления отчета сводной диаграммы или связанного отчета сводной таблицы, линии тренда, соответствующие данным, будут потеряны. При добавлении линии тренда в диаграмму важно подобрать наиболее подходящей вид линии тренда для аппроксимации и сглаживания данных. В Excel существует шесть различных видов линий тренда (рис. 28 ), которые вызываются командой
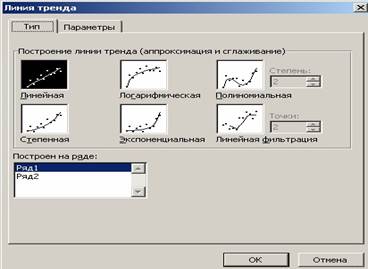
Рис. 28. Вид окна Линия тренда
Арифметическая. Линейная аппроксимация — это прямая линия, наилучшим образом описывающая набор данных. Она применяется в самых простых случаях, когда точки данных расположены близко к прямой. Вообще говоря, линейная аппроксимация хороша для величины, которая увеличивается или убывает с постоянной скоростью.
Формула y =a· x + b, где a - угол наклона и b - координата пересечения оси абсцисс.
Логарифмическая. Логарифмическая аппроксимация хорошо описывает величину, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Описывает как положительные, так и отрицательные величины
Формула y =c·ln x + b, где c и b - константы, ln - функция натурального логарифма.
Полиномиальная. Полиномиальная аппроксимация используется для описания величин, попеременно возрастающих и убывающих. Она полезна, например, для анализа большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов.
Формула y=b+c1x+c2x+c3x3+…c6x6, где b и c1…c6 - константы.
Степенная. Степенное приближение дает хорошие результаты, если зависимость, которая содержится в данных, характеризуется постоянной скоростью роста. Примером такой зависимости может служить график ускорения автомобиля. Если в данных имеются нулевые или отрицательные значения, использование степенного приближения невозможно. Формула y= c·xb, где c и b - константы.
Экспоненциальная. Экспоненциальное приближение следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим. Формула y= c·ebx, где c и b - константы, e - основание натурального логарифма.
Линейная фильтрация (скользящее среднее). Использование в качестве приближения скользящего среднего позволяет сгладить колебания данных и, таким образом, более наглядно показать характер зависимости. Такая линия тренда строится по определенному числу точек (оно задается параметром Шаг). Элементы данных усредняются, и полученный результат используется в качестве среднего значения для приближения. Так, если Шаг равен 2, первая точка сглаживающей кривой определяется как среднее значение первых двух элементов данных, вторая точка — как среднее следующих двух элементов и так далее. Для скользящего среднего значение R-квадрат не может быть отображено.
![]() Ft =
At +
At−1 +…+ At−n+1 n
Ft =
At +
At−1 +…+ At−n+1 n
Степень соответствия линии тренда определяется коэффициентом R2- это число от 0 до 1, которое отражает близость значений линии тренда к фактическим данным. Наиболее достоверна линия тренда, для которой значение R2 ≅ 1.При подборе линии тренда к данным Excel по формулам автоматически рассчитывает значение R2. Это значение можно отобразить на диаграмме.

Задача 46. Добавить и отредактировать линию тренда для графического отображения табличной зависимости y(x):
|
x |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
|
y |
2,39 |
2,81 |
3,26 |
3,75 |
4,14 |
4,52 |
4,85 |
5,25 |
5,56 |
Решение. Для решения задачи выполним последовательность действий:
· Для данной таблицы построим график, выделим область графика для перехода в меню Диаграмма.
· Выберем команду Добавить линию тренда, на экране появится диалоговое окно (рис. 28).
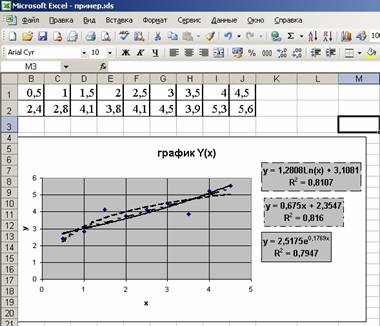
Рис. 29. Построение линии тренда
· Выберем «Логарифмическая» тип регрессионной линии тренда;
· Для вывода формулы и значения R2 откроем закладку Параметры и установим (∨)- флажок напротив соответствующих строк ( рис. 28).
· Для прогноза в закладке Параметры установим необходимые параметры: Прогноз вперед (назад) на один или несколько периодов.
· Для форматирования линии тренда щелкнем на ней правой кнопкой мыши и выберем в контекстном меню команду Форматирование линии тренда, установим пунктирный вид линии.
· Аналогичные действия выполним для других типов линии тренда.
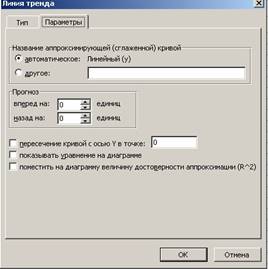
Рис. 30. Вид закладки окна Линия тренда - Параметры
Задача 46. Из приведенных данных создать в Excel таблицу зависимостей Y(x). Построить диаграмму. Создать не менее трёх линий тренда различного типа с прогнозами. Отформатировать диаграмму и линии тренда согласно примера.
|
N |
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
Y(x) |
85,22 |
3,43 |
1,19 |
40,89 |
61,31 |
26,03 |
28,89 |
76,69 |
16,98 |
25,42 |
11,47 |
|
2 |
Y(x) |
81,43 |
1,43 |
73,33 |
92,61 |
36,91 |
1,42 |
73,30 |
8,33 |
39,61 |
55,72 |
91,90 |
|
3 |
Y(x) |
95,20 |
54,71 |
14,89 |
91,78 |
71,27 |
65,45 |
73,29 |
49,64 |
31,45 |
57,10 |
5,61 |
|
4 |
Y(x) |
88,78 |
12,82 |
9,03 |
13,11 |
38,28 |
97,11 |
23,00 |
90,79 |
58,71 |
57,50 |
18,11 |
|
5 |
Y(x) |
34,22 |
41,01 |
89,76 |
83,53 |
58,50 |
14,28 |
80,03 |
20,18 |
34,58 |
95,81 |
51,00 |
|
6 |
Y(x) |
72,15 |
91,93 |
51,76 |
95,25 |
5,43 |
26,79 |
5,97 |
85,62 |
9,55 |
56,67 |
27,90 |
|
7 |
Y(x) |
76,16 |
52,37 |
74,87 |
18,21 |
71,08 |
65,96 |
68,02 |
19,74 |
15,37 |
96,59 |
39,01 |
|
8 |
Y(x) |
32,10 |
28,14 |
54,72 |
97,21 |
22,92 |
34,86 |
1,68 |
81,13 |
41,09 |
48,08 |
80,96 |
|
9 |
Y(x) |
5,83 |
63,44 |
53,94 |
55,15 |
1,22 |
5,47 |
12,28 |
88,44 |
31,06 |
47,37 |
90,57 |
|
10 |
Y(x) |
44,02 |
37,72 |
37,45 |
20,54 |
46,17 |
75,16 |
80,14 |
60,75 |
74,86 |
48,64 |
12,98 |
|
11 |
Y(x) |
11,01 |
41,83 |
96,15 |
44,78 |
97,35 |
28,94 |
37,09 |
70,51 |
16,72 |
76,76 |
95,27 |
|
12 |
Y(x) |
57,88 |
77,03 |
76,64 |
50,98 |
65,23 |
45,08 |
14,54 |
98,74 |
68,85 |
76,19 |
52,11 |
1. Златопольский Д.М. 1700 заданий по Microsoft Excel. – СПб.: БХВ- Петербург, 2003.-544 с.
2. БеляевВ.В., ВиноградоваТ.А, КосовцеваТ.Р. Информатика. Метод. указания по выполнению контрольных работ для студентов заочной формы обучения. – СПб.: СПГГИ(ТУ), 2004.-40 с.
3. РудиковаЛ.В. Microsoft Excel длястудента. – СПб.: БХВ-Петербург, 2005.-368 с.
4. Леоненков А. В. Решение задач оптимизации в среде MS Excel. / А.В. Леоненков. СПб.: БХВ – Петербург, 2005.
5. Лавренов С. М. Excel. Сборник примеров и задач / С. М. Лавренов. М.: Финансы и статистика, 2000.
6. Уэллс Э. Microsoft Excel 97: Разработка приложений / Э. Уэллс, С. Хешбаргер, пер. с англ. М.: Microsoft Press, 1998.

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена Программа развития государственного образовательного учреждения высшего профессионального образования «СанктПетербургский государственный университет информационных технологий, механики и оптики» на 2009–2018 годы.
![]()
КАФЕДРА КОМПЬЮТЕРИЗАЦИИ И ПРОЕКТИРОВАНИЯ ОПТИЧЕСКИХ ПРИБОРОВ
Кафедра Компьютеризации и проектирования оптических приборов была основана в 1939 году. Она была призвана подготавливать инженеров по проектированию военных оптических приборов.
Возглавил кафедру известный специалист в области военных оптикомеханических приборов профессор К.Е. Солодилов. На кафедру из Государственного оптического института пришли работать профессора Резунов М.А. и Цуккерман С.Т. Под их руководством на кафедре проводилась также и научно-исследовательская работа. Были разработаны, например, конструкции новых прицелов: пулеметного ПП1, авиационного АСП, ракурсного курсового.
В послевоенный период времени до 1970 года кафедру возглавлял профессор С.Т. Цуккерман, с 1971 по 1984 гг. заведовал кафедрой Сухопаров С.А., в 1985–90 гг. руководил кафедрой заслуженный деятель науки и техники профессор Зверев В.А.. С 1990 кафедрой заведует их ученик профессор Латыев С.М.
Выпускники кафедры всегда славились как хорошие конструкторы, благодаря сильной проектно-конструкторской и научно-педагогической школе, созданной Солодиловым К.Е., Цуккерманом С.Т., Резуновым М.А., Кулагиным В.В., Сухопаровым С.А.. Сотрудниками школы написано около двадцати монографий, учебных пособий и справочников по проектированию оптических приборов, ставших настольными книгами студентов и инженерно-технических работников оптической промышленности.
Основные научные направления работы кафедры связаны с разработкой теоретических основ конструирования оптических приборов, их точностного расчета и юстировки, автоматизацией функционирования приборов и их проектирования, а также с созданием автоматизированных измерительных фотоэлектрических приборов.
На кафедре были разработаны приборы различного назначения:
• Прибор для измерения скоростей и давления жидкостей;
• Кинематомер для контроля точности зубчатых колес и редукторов;
• Стенд для контроля прецизионных муфт;
• Телевизионный дальномер;
• Стенд для контроля надежности биноклей; • Фотоэлектрический автоколлиматор;
• Цифровой индикатор перемещений.
По результатам научных исследований аспирантами и сотрудниками кафедры были защищены десятки кандидатских и докторских диссертаций. В настоящее время кафедра имеет четыре специализации выпускников:
¾ «Специальные оптические приборы» – подготовка инженеров (магистров) по разработке, юстировке, контролю и обслуживанию оптической техники военного назначения, а также космическим и гражданским приборам, которые эксплуатируются в специальных условиях или имеют особые характеристики;
¾ «Сборка, юстировка, испытание и контроль оптических приборов» - подготовка инженеров (бакалавров) по производству и эксплуатации оптических приборов.
¾ «Метрология и сертификация оптико-электронных приборов» - подготовка инженеров (бакалавров) для метрологических служб и организаций осуществляющих сертификацию продукции.
Студенты, обучающиеся на кафедре, имеют усиленную подготовку по использованию средств автоматизированного конструирования, контролю, юстировке и испытанию приборов, вопросам обеспечения точности их функционирования.
На кафедре имеются учебные лаборатории: Приборов технического зрения; Военных приборов; Оптических приборов; Контроля и юстировки приборов, Метрологии и сертификации оптико-электронных приборов, а также Конструкторский класс. Ряд учебных занятий по военным и космическим приборам проводится в лабораториях базовых кафедр при ГОИ и ЛОМО.
По учебной и научной работе кафедра имеет многолетнее сотрудничество с Техническим университетом Ильменау (Германия), благодаря которому наиболее успевающие студенты, аспиранты и сотрудники кафедры стажируются в лабораториях этого университета.
Иванов Александр Николаевич Каракулев Юрий Александрович
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ С ПРИМЕНЕНИЕМ
ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL
Учебное пособие
В авторской редакции
Дизайн Ю.А. Каракулев
Верстка Ю.А. Каракулев
Редакционно-издательский отдел Санкт-Петербургского государственного университета информационных технологий, механики и оптики
Зав. РИО Н.Ф. Гусарова
Лицензия ИД № 00408 от 05.11.99
Подписано к печати
Заказ №
Тираж 50
Отпечатано на ризографе
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.