Данный учебник используется в презентации "Выполнение заданий по алгебре для 7класса,ФСУ"

(с)

ФГОС

ДЛЯ ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ

под редакцией С. А. ТЕЛЯКОВСКОГО

Рекомендовано

Министерством образования и науки Российской Федерации

Москва

« Просвещение»

2013

удк 373.167.1:512 ББК 22.14я72

А45

Авторы: Ю. Н. Макарычев, Н. Г. Миндюк,

К. И. Нешков, С. Б. Суворова

На учебник получены положительные заключения

Российской академии наук 10106-5215/579 от 14.10.11.) и Российской академии образования (N2 01-5/7д-ЗЗ6 от 17.10.11.)

Алгебра. 7 класс : учеб. для общеобразоват. учреждений /

А45 [Ю. Н. Макарычев, Н, Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — М. : Просвещение, 2013.

256 с. : ил. — ISBN 978=5-09-018967-5.

Данный учебник является первой частью трёхлетнего курса алгебры для общеобразовательных школ. Новое издание учебника дополнено и переработано. Его математическое содержание позволяет достичь планируемых результатов обучения, предусмотренных Федеральным государственным образовательным стандартом основного общего образования. В задачный материал включены новые по форме задания: задания для работы в парах и задачи-исследования. В конце учебника приводится список литературы, до-

полняющей его.

удк 373.167.1:512 ББК 22.14я72

ISBN 978-5-09-018967-5 Издательство «Просвещение», 2013 Художественное оформление.

Издательство «Просвещение», 2013

Дорогие семиклассники1

Вы начинаете изучать новый учебный предмет — алгебру, являющуюся одним из важнейших разделов математики.

Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов решения разнообразных задач. Алгебра используется в современном мире очень широко: в физике, биологии, экономике, информатике, архитектуре и др.

Изучая математику в 5 и 6 классах, вы научились выполнять различные действия с целыми числами и дробями, находить корни уравнений, решать текстовые задачи. В 7 классе вы узнаете ещё много нового. Вы научитесь выполнять различные тождественные преобразования: сложение, вычитание и умножение многочленов, разложение многочленов на множители и многое другое. Это даст вам возможность решать разнообразные задачи. Впервые вы узнаете о способах решения систем уравнений с двумя переменными. Теперь вы сможете решать текстовые задачи, используя не только уравнения с одной переменной, но и системы уравнений с двумя переменными. Вы познакомитесь со свойствами некоторых функций, научитесь строить их графики. Знания и умения, приобретённые на уроках алгебры в 7 классе, помогут вам при изучении многих школьных предметов: геометрии, информатики, физики, химии и др.

Надеемся, что, занимаясь по этому учебнику, вы полюбите новый учебный предмет — алгебру. Для этого, прежде всего, написанное в нём должно быть понятно. Поэтому в объяснительных текстах подробно разъясняется новый материал, приводятся решения различных задач. Они помогут вам разобраться в изучаемых приёмах преобразования выражений, решения уравнений, построения графиков функций и др. Материал, который

нужно запомнить, печатается на цветном фоне, чтобы вы обратили на него внимание. Если вы забыли что-то из ранее изученного, то можете обратиться к разделу «Сведения из курса математики 5—6 классов» . Контрольные вопросы и задания, помещённые в конце каждого параграфа, позволят вам задуматься о сути изученного материала.

В учебнике вам предлагаются разнообразные упражнения. Надеемся, что вы примете активное участие в выполнении упражнений под названием «задача-исследование», рассчитанных на коллективное обсуждение приёмов решения, а также заданий, предназначенных для работы в парах. Выполняя такие задания, вы научитесь прислушиваться к мнению товарищей и отстаивать свою позицию. При работе с учебником рекомендуем использовать специальный диск, где предлагаются упражнения, которые вы можете выполнить на компьютере.

Если вы интересуетесь математикой, то ваше внимание, безусловно, привлечёт материал рубрики «Для тех, кто хочет знать больше», помещённый в конце каждой главы. Специально для ребят, находящих радость в решении непростых задач, в учебнике помещены «Задачи повышенной трудности».

Конечно, многим из вас любопытно узнать, как и почему зарождался и затем развивался тот или иной раздел алгебры. Для ответа на эти вопросы в учебнике даются «Исторические сведения».

Желаем вам успехов в изучении нового интересного предмета алгебры.

В учебнике используются следующие условные обозначения:

— материал, который важно знать

— текст, который нужно запомнить

— начало решения задачи

— окончание решения задачи

• — начало обоснования утверждения или вывода формулы

— окончание обоснования или вывода

19. — задание обязательного уровня

— задание повышенной трудности

— упражнения для повторения

УРАВНЕНИЯ

В этой главе вы повторите начальные сведения из алгебры, с которыми познакомились в 5—6 классах. Вам уже приходилось находить значения выражений с переменными, сравнивать их, решать уравнения, применять их при решении несложных задач. Теперь эти знания и умения будут расширены. Вы узнаете, что называется тождеством, тождественным преобразованием, научитесь выполнять тождественные преобразования выражений с переменными и применять их при решении уравнений. Расширится круг задач, которые вы сможете решать с помощью уравнений. Вы сделаете первые шаги в изучении статистики — важной науки, помогающей разбираться в закономерностях явлений, происходящих в природе и обществе.

ВЫРАЖЕНИЯ

1 . Числовые выражения

Решим задачу:

«Туристы в течение двух часов ехали на велосипедах по шоссе со скоростью 16 км/ч, а затем шли лесом ещё 7 км. Какова длина всего маршрута?»

По шоссе туристы проехали 16 • 2 км, а лесом прошли 7 км. Поэтому длина всего маршрута равна (16 • 2 + 7) км, т. е. 39 км.

Решая задачу, мы получили числовое выражение 16 • 2 + 7.

Числовые выражения составляются из чисел с помощью знаков действий и скобок. Приведём ещё примеры числовых выражений: 43 : 5; 9,6 - 3 . 1,2; 5. (7,4 - 6,1).

Найдём, например, значение выражения 12 • 6 — 35 • 7. Для этого мы должны, соблюдая принятый порядок действий, выпол-

нить сначала умножение и деление, а затем вычитание:

1) 12 72; 2) 35 : 7 = 5; 3) 72 - 5 = 67. Число 67 — значение выражения 12 • 6 — 35 : 7.

Если в выражении встречается деление на нуль, то это выражение не имеет числового значения, так как на нуль делить нельзя. О таких выражениях говорят, что они не имеют смысла.

Например, не имеют смысла такие выражения, как

1. Найдите значение выражения:

а) 6,965 + 23,3;	г) 6,5 • 1,22;	ж) 53,4 : 15;
6) 50,4 - 6,98;	д) 0,48 • 2,5;	з) 16,94 : 2,8;
в) 88 - 9,804;	е) 0,016 • 0,25;	и) 75 : 1,25.

2. Выполните действия:

а) 481,92 : 12 - 20,16; 6) 1,08 • 30,5 - 9,72 : 2,4.

З. Найдите значение выражения:

а) 3,6 : 0,08 + • 2,5; 6) (9,885 - 0,365) : + 4,4.

з 4

в)

д)

ж) 22 : 1 2;

10 15 '

7 7

		5
5.	Выполните действие:
	г) 1,2 • (-5);	ж) 38 : (-0,19);
	б) —2,4 + 5,6; д) —8 • 4,5;	з) -16 : 0,2;
	в) -2,1 - 3,2; е) -0,9 • (-0,1);	и) —6,4 : (—8).
6.	Вычислите:

4. Выполните действие:

и) 3 ¹. -1! .

з 4

2 7

г) ж) - • (-49);

6) -2 ²+ 4з д) з) —16: 4

6			Глава
6
	7.	Найдите:
		а) 1 % числа 240;		в) 120 ⁰/0 числа 8;
		б) 40 ⁰/0 числа 15;		г) 9,5 ⁰/0 числа 280.

8. На пакете молока написано, что в молоке содержится 3,2 ⁰/0 жира, 2,596 белка и 4,7 % углеводов. Какое количество каждого из этих веществ содержится в стакане (200 г) молока?

9. В фермерском хозяйстве собирали по 36 ц пшеницы с гектара. Применение интенсивной технологии позволило увеличить производство пшеницы на той же площади на 25 ⁰/0 . Сколько центнеров пшеницы стали собирать с 1 га в этом фермерском хозяй-

стве?

10. За несколько книг уплатили 320 р. Стоимость одной из книг составила 30 ⁰/0, а другой — 45 ⁰/0 израсходованных денег. На сколько рублей первая книга дешевле второй?

11.] Используя три раза цифру 2, составьте выражение, значение которого равно:

12. Составьте какое-нибудь выражение, содержащее два знака действия, значение которого равно: а) 12; б) О.

13. Из данных выражений выберите выражение, не имеющее смысла.

1. 126 : (36 • 2 - 5 . 8) з. (1,7 . 2 - 3,4) : 11

2,6 - 13 . 0,57

2.4.

8 - 0,4 . 2

14. Составьте какое-либо выражение, не имеющее смысла.

15. Составьте числовое выражение для решения задачи: «Из двух населённых пунктов, расстояние между которыми 40 км, вышли одновременно навстречу друг другу два пешехода. Какое расстояние будет между ними через З ч, если известно, что скорость одного пешехода 4 км/ч, а скорость другого пешехода 5 км/ч?»

16. Решите задачу, составив выражение: «Один рабочий изготовляет за час 7 деталей, а другой — 9 деталей. Сколько деталей они изготовят за 4 ч?»

17. Используя термины «сумма» , «разность», «произведение» и «частное», прочитайте выражение:

д) 2 . 9,5 + 14; и) - (3,2 + 1,8);

6) е) (10 - 2,7) : 5; к) (5,74 - 1,24) • 3,6;

ж) 6,1 • (8,4 : 4); л) 8 - (1,71 + 0,19);

з) (6,4 + 7) : 2; м) 0,36 : - 1,78.

ё 1.

18. (ЗаДача-исслеДование.) Из 36 учащихся класса каждый изучает хотя бы один иностранный язык — английский или немецкий. Известно, что 25 учащихся изучают английский язык, а 18 учащихся — немецкий язык. Сколько процентов всех учащихся изучают оба языка?

1. Укажите число учащихся, изучающих хотя бы один из этих языков.

2. Вычислите число учащихся, изучающих оба языка — английский и немецкий.

З) Найдите, сколько процентов учащихся изучают оба языка.

2. Выражения с переменными

Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за З ч— 60 • З км, за 5 ч— 60 • 5 км, за 5,5 ч— 60 • 5,5 км. Вообще за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t — выраже1-шејИ с переменной.

Приведём ещё пример. Пусть длины сторон прямоугольника равны а см и Ь см. Тогда его площадь равна ab см ². Выражение ab содержит две переменные а и Ь. Оно показывает, как находить площадь прямоугольника при различных значениях а и Ь. Например: если а = 8 и Ь = 11, то ab = 8 11 = 88; если а = 25 и Ь = 4, то ab = 25 • 100.

_ wr.m Если в выражение с переменными подставить вместо каждой переменной какое-либо её значение, то получится ! числовое выражение. Его значение называют значением выражения с переменными при выбранных значениях переменных.

Так, число 88 есть значение выражения ab при а = 8 и Ь = 11, число 100 есть значение этого выражения при а = 25 и Ь = 4.

Рассмотрим выражение При любом Ь * З можно найти его значение. Например, если Ь = 13, то = 1,3.

При Ь = З значение этого выражения найти нельзя, так как в этом случае делитель Ь — З равен нулю. Говорят, что при Ь * З выражение имеет смысл, а при Ь = З оно не имеет смысла.

8	Глава

Некоторые выражения имеют смысл при всех значениях переменных. Примерами могут служить выражения

8- 10

х(х + 1), ау — 4,

Выражения с переменными используются для записи формул. Рассмотрим примеры.

Любое чётное число т можно представить в виде произведения числа 2 и целого числа п, т. е.

т = 2n.

Если в эту формулу вместо п подставлять целые числа, то значениями переменной т будут чётные числа. Формулу т = 2n называют формулой чётного числа.

Формулу т = 2n + 1, где п — целое число, называют формулой нечётного числа.

Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу.

Например, формулу числа, кратного З, можно записать так: т = Зп, где п — целое число.

19. Найдите значения выражения:

а) 4х — 12 при х = 7; О; —5;

б) 2,8 — 0,5у при у = З; О; —6.

20. Заполните таблицу, вычислив значения выражений и —3х + 1 для указанных значений х:

	-2	-1	1	2	4	5
3х — 1

Какими числами являются соответственные значения выражений 3х — 1 и —3х + 1?

И.: Найдите значения выражений 10 — 2у и 10 + 2! и запишите их в соответствующие клетки таблицы:

	—3	-1	2	З	4	6
10 - 2у
10 + 2у

22. Какие значения принимают сумма х + у и произведение ху при следующих значениях переменных:

а) х = 1,2, у = —2,5; в) х = 0,1, у = 0,2; 6) х = -0,8, З; г) х = —1 4 у —1,6?

Найдите значение выражения 5m — За, если:

б) т = 0,2, п = —1,4.

5 3 '

24. Вычислите значение выражения — х — у, если:

а) х = 2,4, у = 0,8; в) х = 4,8, у = —2,1; 4,4, у : -3.

Заполните таблицу, вычислив значения выражения а

	5	-2	4	1	6
	-3	з		-1	4
а — 2b

26, Известно, что при некоторых значениях х и у значение выражения х — у равно 0,7. Какое значение принимает при тех же х и у

выражение:

а) 5(х — у);в) г)

27. Известно, что при некоторых значениях а и Ь значение выражения а — Ь равно 4. Чему равно при тех же а и Ь выражение

12 16

? Выберите верный ответ.

28. Вычислите значение выражения:

а) ах — Зу при а = 10, х = —5, у = — 3 '

б) ах + bx + с при а = —, х 2 Ь = -3, с = 5,8.

29. Опытное поле разбили на два участка. Площадь первого участка а га, а второго — Ь га. С каждого гектара первого участка собрали 32 ц пшеницы, а с каждого гектара второго участка собрали 40 ц. Сколько пшеницы собрали с обоих участков? Вычислите при а = 120 и Ь = 80.

30. На стройке работало 5 бригад, по а человек в каждой, и З бригады, по Ь человек в каждой. Сколько человек работало на стройке? Вычислите при а = 25 и Ь = 32.

10	Глава

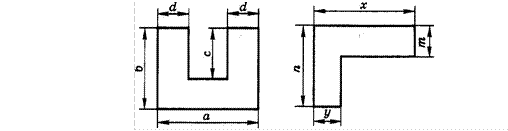
Рис. 2

31. На рисунке 1 указаны длины отрезков (в сантиметрах). Для каждой фигуры составьте выражение для вычисления её площади (в квадратных сантиметрах),

32. Ребро куба равно а м. От этого куба отрезан прямоугольный параллелепипед, высота которого равна h м (рис. 2). Найдите объём оставшейся части.

33. В 250 г водного раствора соли содержалось х г соли. Какой стала концентрация раствора после добавления в него 5 г соли? Выберите верный ответ.

1. -Е • 100 ⁰/0 2. • 100 ⁰/0 з. х • 100 ⁰/0 4. • 100 ⁰/0

250 250 255 255

34. В сплаве олова и свинца массой 20 кг содержалось х кг олова. Каким стало процентное содержание олова в сплаве после добавления в него 2 кг олова?

35. Длина прямоугольника а см, ширина Ь см. Что означает выражение: а) ab; б) 2а + 2b; в) а + Ь; г) 2а?

36. Тетрадь стоит х р., а карандаш стоит у р. Что означает выражение: а) х + у; б) 3х + у; в) 2х + Зу; г)

37. Прочитайте, пользуясь терминами «сумма», «разность», «произведение» и «частное», выражение:

а) тх; д) 2х + 1; ж) ab + bc;

б) 10 + ab; г) т — 8а; з)

38. Запишите в виде выражения:

а) сумму чисел Ь и с;

б) разность чисел а и т;

в) квадрат числа х;

г) куб числа у;

д) сумму числа х и произведения чисел а и Ь;

е) разность числа т и частного чисел х и у;

ж) произведение суммы чисел а и Ь и числа с

з) произведение числа а и суммы чисел х и У.

39. При каких значениях переменной имеет смысл выражение:

18 1

а) 5у + 2; б) в) г) д)

410 - Ь

40. Какое из данных выражений имеет смысл при любых значениях а?

12 5 14 8

1. 2. з. 4.

а2 0²+ 1

41. Составьте формулу числа:

а) кратного 5; б) кратного 10; в) кратного 101.

42. Напишите формулу числа, кратного 7. Найдите по этой формуле два трёхзначных числа, кратных 7.

43. (Для работы в парах.) Докажите, что всякое простое число, начиная с 5, увеличенное или уменьшенное на 1, делится на 6. 1) Проверьте утверждение на примерах. Одному учащемуся рекомендуем взять простые числа из третьего десятка, другому из седьмого десятка.

2) Обсудите друг с другом, из чего следует справедливость указанного свойства.

З) Проведите доказательство.

44. Найдите число, если известно, что:

а) 3 ⁰/0 этого числа равны 1,8;

б) 85 ⁰/0 этого числа равны 17;

в) 130 ⁰/0 этого числа равны 3,9;

г) 6,2 % этого числа равны 9,3.

45. После того как из бидона отлили 30 ⁰/0 молока, в нём осталось 14 л. Сколько литров молока было в бидоне первоначально?

46. Перевыполнив план на 15 ⁰/0, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?

З. Сравнение значений выражений

Решим задачу: «Пшеницей засеяли два опытных участка площадью 48 га и 60 га. С первого участка собрали 1800 ц пшеницы, а со второго 2100 ц. На каком участке урожайность выше?»

Урожайность выражается частным от деления массы пшеницы, собранной с участка, на площадь участка. Чтобы узнать, на каком участке урожайность выше, надо сравнить значения выражений 1800 : 48 и 2100 : 60. Так как 1800 : 48 37,5; 2100 : 60 = 35, то урожайность выше на первом участке.

1 2	Глава

Для любых двух числовых выражений можно установить, равны их значения или нет, и если они не равны, то какое из них больше и какое меньше.

Результат сравнения значений выражений можно записать в виде равенства или неравенства. Например, результат сравнения частных 1800 : 48 и 2100 : 60 можно записать в виде неравенства 1800 : 48 > 2100 : 60.

Если выражения содержат переменные, то для разных значений переменных результат сравнения значений этих выражений может оказаться различным.

Сравним, например, значения выражений 2а и а + 4 при а = О;

Если а = О, то 2а = О и а + 4 = 4, т. е. при а = О верно неравенство 2а 4.

Если а = 4, то 2а = 8 и а + 4 = 8, т. е. при а = 4 верно равенство

Если а = 10, то 2а = 20 и а + 4 = 14, т. е. при а = 10 верно неравенство 2а > а + 4.

Иногда требуется установить, между какими числами заключено значение выражения.

Рассмотрим пример. Пусть при взвешивании металлического шарика установили, что его масса больше 86 г, но меньше 87 г. Обозначим массу шарика (в граммах) буквой т. Тогда результат взвешивания можно записать так: т > 86 и т < 87, или иначе: 86 < т и т < 87.

Два неравенства 86 т и т 87 можно записать в виде двойного неравенства

86 87.

Неравенство 86 < т < 87 читают так: «86 меньше т и т меньше 87» — или короче: «т больше 86 и меньше 87».

Рассмотрим ещё один пример. Число дней в месяце меньше 31 или равно 31. Обозначим число дней в месяце буквой п. Тогда

п < 31 или п = 31.

Вместо этой записи обычно пишут одно неравенство

(читают: «п меньше или равно 31»).

Число дней в месяце больше или равно 28:

п > 28 или п = 28. В таких случаях также пишут короче:

28 (читают: «п больше или равно 28»).

Так как п 28, то 28 п.

Два неравенства 28 п и п 31 можно записать в виде двойного неравенства

Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков и называют нестрогими.

47. Сравните значения выражений: а) 2,06 • 3,05 и 21,28 : 3,5; 1 1 1 1

2 5

6) 97,2 : и 62 - 21,6; г) 16— 3! и 15— 2 1

48. Сравните значения выражений, не вычисляя их:

а) 56 • ²и 56 : ^Щ; , и 2 1 - 1,7;

7 2

6) 9 : и 9 . 0,6; г) 6,13 — 7,57 и -6,13 + 7,57.

49. Сравните значения выражений, не вычисляя их:

а) 6,16 — 7,44 и 7,23 + 8,11; в) 5,7 - 3,11 и 5,7 - 2,16,

5 5

6) 24,12 г) 65,4 — и 65,4

4 6

50. Сравните значения выражений:

а) • и + 0,8 - 0,9; 1 1 1

51. Сравните значения выражений:

а) 9,5 — а и 0,5а при а = 3,8; О; 5;

б) З — с и 4с — 5 при с =

52. Сравните значения выражений:

а) х и —х при х = 8; О; —3; б) х и 100х при х — 5

53. Сравните значения выражений:

а) 5m — 0,8 и 0,8m — 5 при т = —1;

б) ab и а : Ь при а = 4,6, Ь = 0,23.

Верно ли неравенство 2х + 5 < 3х при х = 4,2; 5; 6,5?

55. Прочитайте неравенство:

а) 8,1 < 8,14 < 8,6; г) -40 < -38,7 < -30; 6) 9,865 10; д)

в) -900 < -839 < -800 2,42 < 2! < 2,43.

14	Глава I

56. Запишите в виде двойного неравенства:

а) 8 меньше 13 и 13 меньше 16;

б) 4,1 меньше 4,18 и 4,18 меньше 4,2;

в) 63,5 больше 63 и меньше 64;

г) —8,1 больше —11 и меньше —7;

д) а больше 1,8 и меньше 2,8;

е) х больше а и меньше Ь.

57. Подберите какое-нибудь число, заключённое между числами: а) 8,6 и 8,7;в) —3,6 и —3,7; 8

Результат запишите в виде двойного неравенства.

58. Запишите в виде двойного неравенства:

а) 0,79 больше 0,7 и меньше 0,8;

б) 6! больше 6 и меньше 7;

в) —4,6 больше —10 и меньше О;

г) т больше —16 и меньше —15;

д) К больше 2,65 и меньше 2,66;

е) у больше т и меньше п.

59. На координатной прямой точками отмечены числа а, Ь и с (рис. З). Укажите для каждой точки соответствующее ей число, если известно, что а > Ь и с > а. Составьте из чисел а, Ь и с двойное неравенство с помощью знака <.

60. Прочитайте неравенство:

ж)

в) а э —10,4; е)

61. Верно ли неравенство:

а) х < 5,3 при х = 2,7; 5,3; 6;

б) у » 4,8 при у = 3,5; 4,8; 7,1;

в) 0,6 0,8 при х = 0,5; 0,6; 0,7; 0,8; 0,9;

г) 2,1 2,4 при 2,1; 2,2; 2,3; 2,4; 2,5?

62. Запишите с помощью знаков неравенства:

а) х меньше или равно 8;

б) у больше или равно О;

в) а больше 5 и меньше или равно 7;

г) Ь больше или равно —2 и меньше 1.

5 1 .

63. Запишите в виде неравенства:

а) х — отрицательное число;

б) т — положительное число;

в) у — неотрицательное число;

г) г — неположительное число.

64. Запишите в виде двойного неравенства:

а) х больше или равно 11 и меньше 12;

б) у больше 50 и меньше или равно 100;

в) а больше 350 и меньше 400;

г) Ь больше или равно —100 и меньше или равно —10.

65. Один автомобиль прошёл 700 км за х ч, а другой автомобиль прошёл 630 км за у ч. Сравните средние скорости автомобилей, если:

а) х = 12,5, 10,5;

66. Сколько процентов составляет:

а) число 8 от числа 200; б) число 2,1 от числа 14?

67. В результате рационализации производства удалось сократить число рабочих на комбинате. Вместо 1600 их осталось 1200. На сколько процентов сократилось число рабочих?

68. Найдите значение выражения:

а) 37,6 - 5,84 + 3,95 - 8,9; в) 17,1 • : 4,5 • 0,5;

6) 81 - 45,34 + 19,6 + 21,75; г) 81,9 : : 0,28 • 1,2.

69. Запишите в виде выражения:

а) сумму числа х и произведения чисел а Ь;

б) частное от деления числа а на разность чисел Ь и с;

в) произведение суммы чисел х и а и разности чисел х и Ь.

Контрольные вопросы и задания

Приведите пример числового выражения

НЫМИ.

Имеет ли смысл выражение:

2 . 16 - 32 '

Сравните значения выражений х + 3 и

Приведите пример двойного неравенства Как читаются знаки и Какое и какое нестрогим? Приведите пример строгого неравенства.

и выражения с перемен-

42 - 6 - 7

37 - 11

3х при х = —4; 1,5; 5.

и прочитайте его.

неравенство называется строгим строгого неравенства, не-

16	Глава

ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ

4, Свойства действий над числами

Напомним основные свойства сложения и умножения чисел.

1) Переместительное свойство: для любых чисел а и Ь верны равенства а + Ь = Ь + а, ab = ba.

2) Сочетательное свойство: для любых чисел а, Ь и с верны равенства

(а + Ь) + с = а + (Ь + с), (ab)c = a(bc).

З) Распределительное свойство: для любых чисел а, Ь и с верно равенство

а (Ь + с) = ab + ас.

Из переместительного и сочетательного свойств сложения следует:

$ в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.

Пример 1. Вычислим сумму 1,23 + 13,5 + 4,27.

Для этого удобно объединить первое слагаемое с третьим. Получим

1,23 + 13,5 + 4,27 = (1,23 + 4,27) + 13,5 = + 13,5 = 19.

Из переместительного и сочетательного свойств умножения следует:

в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.

Пример 2. Найдём значение произведения 1,8 • 0,25 • 64 • 0,5. Объединив первый множитель с четвёртым, а второй — с третьим, получим

1,8 • 0,25 • 64 • = (1,8 • 0,5) • (0,25 64) =

= • 14,4. <

Распределительное свойство справедливо и в том случае, когда число умножается на сумму трёх и более слагаемых.

Например, для любых чисел а, Ь, с и d верно равенство аф + с + d) = ab + ас + ad.

Мы знаем, что вычитание можно заменить сложением, прибавив к уменьшаемому число, противоположное вычитаемому:

Это позволяет числовое выражение вида а — Ь считать суммой чисел а и —b, числовое выражение вида а + Ь — с — d считать суммой чисел а, Ь, —с, —d и т. п. Рассмотренные свойства действий справедливы и для таких сумм.

Пример 8. Найдём значение выражения 3,27 — 6,5 — 2,5 + 1,73.

Это выражение является суммой чисел 3,27, —6,5, —2,5 и 1,73.

Применив свойства сложения, получим

3,27 - - 2,5 + 1 73 = (3 27 + 1,73) + (-6,5 - 2,5) =

1 5

Пример 4. Вычислим произведение 36 •

4 18

1 5 1

Множитель можно рассматривать как сумму чисел

4 18 4

и • Используя распределительное свойство умножения, по18 лучим

36 . = 36 1 - 36 . 5

4 18

70. Какие свойства действий позволяют, не выполняя вычислений, утверждать, что верно равенство:

а) 247 + 35 = 35 + 247; в) 14 + (16 + 97) = (14 + 16) + 97; 6) 84 • 19 = 19 • 84; г) 25 • (4 + 7) = 25 • 4 + 25 • 7?

71. Вычислите наиболее рациональным способом:

а) 3,17 + 10,2 + 0,83 + 9,8; в) 15,21 - - 4,7 + 6,79; 6) 4,11 + 15,5 + 0,89 + 4,4; г) -4,27 + - 5,73 - 3,3.

72. Найдите значение выражения:

а) 8,91 + 25,7 + 1,09; в) 7,15 - 9,42 + 12,85 - 0,58; 6) 6,64 + 7,12 + 2,88; г) 18,9 - - 5,2 - 4,1.

73. Выполните действие и объясните, какие свойства сложения были при этом использованы:

а) 5 ²+13з 6) 19 ²+ 10!. 4' з

18	Глава

74. Найдите значение выражения:

а) 5 ²—

4 4 7

75. Вычислите наиболее рациональным способом:

а) 50 • 1,34 • 0,2; в) 25 • (-16,8) • 4; 6) -75,7 • • 20; г) 0,47 • • 25.

76. Используя распределительное свойство умножения, выполните действие:

8 в) 2 ²5 • 8 5 12

77. Найдите значение выражения:

а) • 6,8 + • 3,2; 6) 12,4 • 14,3 - 12,4 • 4,3.

78. Вычислите:

а) 15,7 • 8,09 + 16,7 2,91; 6) 4,08 • 27,9 - 17,9 • 4,08.

79. Докажите, что:

а) сумма 24 • 17 + 17 • 6 делится на 5;

б) сумма 34 • 85 + 34 • 36 делится на 11.

80. Для детского сада купили 5 наборов карандашей и 10 альбомов для рисования. Набор карандашей стоит а рублей, а альбом стоит Ь рублей. Какова стоимость покупки?

t81. Автомобиль двигался t ч со скоростью 60 км/ч и р ч со скоростью 50 км/ч. Какова средняя скорость автомобиля?

82. 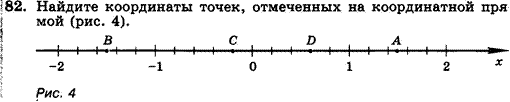Найдите координаты точек, отмеченных на координатной прямой (рис. 4).

83. Отметьте на координатной прямой точки, соответствующие числам 1,4; -1,7; 0,8; -1,2.

84. (Для работы в парах.) Расположите в порядке убывания числа:

а) 6 ²; 6,3; 6 ²; в) -1,07; -1,7; о; 7

6) 2,01; 2,001; 2 ²; г) -3,04; -3,02; -3,19.

Ответ запишите в виде двойного неравенства.

1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их.

2) Проверьте друг у друга правильность выполнения заданий. З) Исправьте ошибки, если они допущены.

5. Тождества. Тождественные преобразования выражений

Найдём значения выражений З (х + у) и 3х + Зу при х = 5,

Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений З(х + у) и 3х + Зу равны.

Рассмотрим теперь выражения 2х + у и 2ху. При х = 1, у = 2 они принимают равные значения:

Однако можно указать такие значения х и у, при которых значения этих выражений не равны. Например, если х = З, у = 4, то

О п р е д е равны при

' ЕЖА л е н и е. Два выражения, значения которых любых значениях переменных, называются тождественно равными.

Выражения З (х + у) и 3х + Зу являются тождественно равными, а выражения 2х + у и 2ху не являются тождественно равными.

20	Глава

Равенство

верно при любых значениях х и у. Такие равенства называются тожДествами.

тождеством!.

' 11 Ж

О п р е д е л е н и е. Равенство, верное при любых значениях переменных, называется

Тождествами считают и верные числовые равенства.

С примерами тождеств вы уже встречались. Так, тождествами являются равенства, выражающие основные свойства действий над числами:

ab = ba, (ab)c = a(bc), а (Ь + с) = ab + ас.

Можно привести и другие примеры тождеств:

а • 1 = а, а • (—6) = —ab, (—а) (—b) = ab.

Чтобы найти значение выражения ху — .rz при заданных значениях х, у и 2, надо выполнить три действия. Например, при х = 2,3, у = 0,8, = 0,2 получаем ху - .rz = 2,3 • - 2,3 • = 1,84 - 0,46 = 1,38.

Этот результат можно получить, выполнив лишь два действия, если воспользоваться выражением х (у — г), тождественно равным выражению ху — xz:

- г) = - 0,2) = 2,3 • = 1,38.

Мы упростили вычисления, заменив выражение ху — .rz тождественно равным выражением х (у — г).

Замену одного выражения другим, тождественно равным ему выражением, называют тожДественны.м преобразованиеж или просто преобразованием выражения.

Ъ—ъ ВЗАА_е АПьь»

Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.

Тождественные преобразования выражений широко применяются при вычислении значений выражений и решении других задач.

¹В дальнейшем понятия «тождественно равные выражения» и «тождество» будут уточнены.

Некоторые тождественные преобразования вам уже приходилось выполнять, например приведение подобных слагаемых, раскрытие скобок. Напомним правила выполнения этих преобразований:

I чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть; если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки; если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.

Пример 1, Приведём подобные слагаемые в сумме 5х + 2х — 3х.

Воспользуемся правилом приведения подобных слагаемых:

5х + - 3х = (5 + 2 - 4х.

Это преобразование основано на распределительном свойстве умножения.

Пример 2. Раскроем скобки в выражении 20 + (Ь - зс).

Применим правило раскрытия скобок, перед которыми стоит знак «плюс»:

20 + Ф - зс) = + ь - зс.

Проведённое преобразование основано на сочетательном свойстве сложения.

Пример З. Раскроем скобки в выражении а — (4b — с).

Воспользуемся правилом раскрытия скобок, перед которыми стоит знак «минус»:

а — (46 — с) = а — 46 + с.

Выполненное преобразование основано на распределительном свойстве умножения и сочетательном свойстве сложения. Покажем это. Представим в данном выражении второе слагаемое — (46 — с) в виде произведения (—1)(4b — с):

а — (4b — с) = а + (—1)(4b — с).

Применив указанные свойства действий, получим а — (4b — с) = а + (—1)(4b — с) = а + (—4b + с) = а — 4b + с.

Глава

85. Какие свойства действий позволяют утверждать, что тождественно равны выражения:

а) ab + 16с и 16с + ab; в) ху + 3 и З + ху;

г) + с) и 5b + 5с?

86. Являются ли тождественно равными выражения:

а) (2a)(7b) и 14ab;

б) —2а + 2а и О; г) (х — у)? и (у — х)²?

87. Являются ли тождественно равными выражения:

а) 2 + 8ba и 8ab + 2;

6) 2х + 7 и их + 7); г) (а + Ь) • 2 и 2а + 2b?

88, Какие свойства действий позволяют утверждать, что данное равенство является тождеством:

а) 12 (а — 4) = 12а - 48; б) (х — х)а = О?

89. Какое из данных равенств не является тождеством?

1. 6 (х — у) = 6х — бу

2. 25(а - а) = 25

90. Упростите выражение, используя переместительное и сочетательное свойства умножения:

а) —6,2а • 5; в) 0,3х • (—12у);

6) 4с • (-1,25); г) -0,1b (-2,30.

91. Упростите выражение:

а) 1,6 • (-0,20; б) —6,4а • (—5с).

92. Преобразуйте выражение в тождественно равное, используя распределительное свойство умножения:

в) -23 • (2а - ЗЬ + 1);

г) 1,5 • (—3х + 4у — 52).

93. Замените выражение тождественно равным, используя распределительное свойство умножения:

а) 1,2 • (5 - а); в) 2,5 • (4х - бу - 2);

б) (т — 4х) • (—6); г) -0,1 • (100а + 10b - с).

94. Среди выражений 2(b — а), —2 (а — Ь), —2а — 26, —2а + 2b найдите те, которые тождественно равны выражению 2b — 2а.

95. Приведите подобные слагаемые:

а) 5а + 27а — а; в) 6х- 14 - 13х + 26; 6) 12b - 17b - Ь; г) —8 — у + 17 — 10у.

96. Приведите подобные слагаемые:

а) 1За + - 2а - Ь; в) —5,1а — 4b — 4,9а + Ь;

б) 41х — 58х + бу — у; г) 7,5х + у — 8,5х — 3,5у.

97. Приведите подобные слагаемые:

а) 8х — бу + 7х — 2у; в) 3,5b - 2,4с - о,6с - 0,7b•,

б) 27р + 14q — 16р — 3q; г) 1,6а + 4х — 2,8а — 7,5х.

98. Раскройте скобки:

99. Запишите без скобок выражение:

100. Упростите выражение:

в) 64 - (14 + 7х);

6) 7 + (12 - 26); г) 38 + - 8).

101. Раскройте скобки и приведите подобные слагаемые:

а) х + (2х + 0,5); в) 4а — (а + 6);

24

б) 3х — (х — 2); г) 6b + (10 — 4,5b).

102. Упростите выражение и найдите его значение:

а) (5х — 1) — (2 — 8х) при х = 0,75;

б) (6 — 2х) + (15 — 3х) при х = —0,2;

в) 12 + 7х — (1 — 3х) при х = -1,7;

г) 37 — (х — 16) + (11х — 53) при х = —0,03.

103. Упростите выражение:

а) (х - 1) + (12 - 7,5х); 6) ер + 1,9) - (7

в) (3 - о,4а) - (10 - О,8а);

104. Докажите, что при любом а значение выражения З (а + 2) - За равно 6.

105. Раскройте скобки и приведите подобные слагаемые:

а) - 5х) + 17х - 10; г) - 1,6а) + з,2а - 9,6; 6) 8(3у + 4) - 29у + 14; д) + 1,7) + 12,5 - 8,5b;

в) 7(2z - 3) + - 12; е) -4 (3,3 - 8с) + 4,8с + 5,2.

106. Упростите выражение и найдите его значение:

а) 0,60 — З) + р + 2 при р = 0,5;

1 14q + 21 при ч = —. з

107. Составьте выражение по условию задачи и упростите его:

а) У Игоря З альбома с марками. В первом альбоме а марок, во втором — на 15 марок больше, чем в первом, а в третьем втрое больше, чем во втором. Сколько марок в трёх альбомах? б) Пётр приобрёл 8 билетов лотереи «Надежда» и 6 билетов лотереи «Удача». Билет лотереи «Удача» стоил а р., а лотереи «Надежда» был на 10 ⁰/0 дороже. Найдите стоимость по-

купки.

108. Сравните значения выражений, не вычисляя их:

1 1 1 1 1 1

б) 3,7 и 3,7 : —

з 3'

в) 5,6 : 2,5 и 5,6 • 2,5.

Ответ запишите в виде неравенства.

109. Техническое перевооружение цеха позволило выпускать в сутки 180 станков вместо 160. На сколько процентов повысился выпуск станков в сутки?

110. Отметьте на координатной прямой точки, соответствующие числам: -3,9; 2,6; -0,7; 3,2; -1,5; 1,25.

Контрольные вопросы и задания

Сформулируйте переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения. Какие выражения называются тождественно равными? Приведите пример тождественно равных выражений.

Какое равенство называется тождеством? Приведите пример тождества.

УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ

6. Уравнение и его корни

Рассмотрим задачу: «На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг на полках станет поровну. Сколько книг на верхней полке?»

5 Уравнения переменной

Обозначим буквой х число книг на верхней полке. Тогда число книг на нижней полке равно 4х. Если с нижней полки переставить на верхнюю 15 книг, то на нижней полке останется 4х — 15 книг, а на верхней будет х + 15 книг. По условию задачи после такой перестановки книг на полках окажется поровну. Значит, 4х — 15 = х + 15.

Чтобы найти неизвестное число книг, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями с одной переменной или уравнениями с одним неизвестным.

Нам надо найти число, при подстановке которого вместо х в уравнение 4х — 15 = х + 15 получается верное равенство. Такое число называют решением уравнения или корнем уравнения.

О п р е д е л е н и е. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Из уравнения

4х — 15 = х + 15

находим, что

15 + 15, 3х = 30, х = 10.

Уравнение 4х — 15 = х + 15 имеет один корень — число 10.

Можно привести примеры уравнений, которые имеют два, три и более корней или не имеют корней.

Так, уравнение (х — 4) (х — 5)(х — 6) = О имеет три корня: 4, 5 и 6. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (х — 4)(х — 5) (х — 6), а значит, и само произведение. При любом другом значении х ни один из множителей в нуль не обращается, а значит, не обращается в нуль и произведение. Уравнение х + 2 = х не имеет корней, так как при любом значении х левая часть уравнения на 2 больше его правой части.

Уравнение х ²= 4 имеет два корня — числа 2 и —2. Уравнение (х — 2) (х + 2) = О также имеет корни 2 и —2. Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными.

26	Глава

При решении уравнений используются следующие свойства:

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Например, равносильны уравнения 5х = 2х + 7 и 5х — 2х = 7, равносильны также уравнения 6х = 2х + 8 и 3х = х + 4.

Указанные свойства уравнений можно доказать, опираясь на свойства числовых равенств: если к обеим частям верного равенства прибавить одно и то же число или обе части верного равенства умножить или разделить на одно и то же отличное от нуля число, то получится верное равенство.

111. Является ли число З корнем уравнения:

а) 5(2х - 1) = 8х + 1;

112. Какие из чисел —2, — 1, О, 2, З являются корнями уравнения:

а) .x ²= 10 - зх; 6) х(х ²- 7) = 6?

Является ли корнем уравнения х (х — 5) = 6 число:

11,4, Докажите, что каждое из чисел 7, —3 и О является корнем уравнения х(х + З)(х — 7) = О.

Докажите, что каждое из чисел 1,2 и —1,2 является корнем уравнения х ²= 1,44. 116. Докажите, что:

а) корнем уравнения 1,4 (у+ является любое число;

б) уравнение у — З = у не имеет корней.

117. Имеет ли корни уравнение:

а) 2х + 3 = 2х + 8;

118. Какое из уравнений не имеет корней?

З.

2. 2у=4у

119. Составьте какое-нибудь уравнение, корнем которого является число: а) 8; б) —12.

Уравнения переменной

120. Имеет ли уравнение корни и сколько:

а) lxl = 1; 6) 1х1 = 0; г) lxl = 1,3?

121. Замените:

а) уравнение 0,3х = —4 равносильным уравнением с целыми коэффициентами;

б) уравнение 5х — 4 = 21 равносильным уравнением вида ах = Ь, где а и Ь — некоторые числа.

122. Упростите выражение:

а) (7х - 2) - 1,6 + 1,7х•, 6) (1,20 - 4) + (40 - 4,80);

в) 2,5 (4 - Зу) 2,3;

г) (14 — 3,66) — (12 + 10,46).

123. Найдите значение выражения - з,5т) - 20 + 23т при т = 2,5; 1,2; 40.

124. На координатной плоскости (рис. 5) отмечены точки А, В, С, D, Е и Р. Рис. 5 Найдите их координаты.

125. Отметьте в координатной плоскости точки А ( 4

7. Линейное уравнение с одной переменной

Каждое из уравнений 5х = —4, —0,2х = О, —х = —6,5 имеет вид ах = Ь, где х — переменная, а и Ь — числа. В первом уравнении а 5, Ь = —4, во втором а = —0,2, Ь = О, в третьем а = —1, Ь = —6,5.

Такие уравнения называют линейными уравнениями с одной переменной.

О п р е д е л е н и е. Уравнение вида ах = Ь, где х — переменная, а и Ь — некоторые числа, называется линейным

уравнением с одной переменной.

Выясним, сколько корней может иметь линейное уравнение. Рассмотрим уравнение ах = Ь, в котором коэффициент а не ра-

вен нулю. Разделив обе части уравнения на а, получим х = —. Знаа

чит, линейное уравнение ах = Ь, в котором а О, имеет единственный корень а

Рассмотрим уравнение ах = Ь, у которого коэффициент а равен нулю. Если а = О и Ь О, то уравнение ах = Ь не имеет корней, так как равенство Ох = Ь не является верным ни при каком х. Если а = О и Ь = О, то любое значение х является корнем уравнения, так как равенство Ох = О верно при любом х.

Линейное уравнение ах = Ь при а * О имеет один корень, при а = О и Ь * О не имеет корней, при а = О и Ь = О имеет бесконечно много корней (любое число является его корнем).

Решение многих уравнений сводится к решению линейных уравнений.

Пример. Решим уравнение 4(х + 7) = З — х.

Раскроем скобки:

4х + 28 = з - х.

Перенесём слагаемое —х в левую часть уравнения, а слагаемое 28 в правую часть, изменив при этом их знаки: 4х + х = з - 28. Приведём подобные слагаемые:

5х = -25.

Разделим обе части уравнения на 5:

Применяя свойства уравнений и выполняя тождественные преобразования, мы последовательно заменяли одно уравнение другим, равносильным ему. Значит, корнем уравнения 4 (х+ 7)=З—х является число —5. <

В этом примере исходное уравнение свелось к равносильному линейному уравнению, в котором коэффициент при переменной отличен от нуля.

Если при решении уравнения мы придём к равносильному ему линейному уравнению вида Ох = Ь, то в этом случае либо исходное уравнение не имеет корней, либо его корнем является любое число. Решим уравнение 2х + 5 = 2 (х + 6):

= 2х Ч- 12,

2х - 12 - 5, ох = 7.

Полученное уравнение не имеет корней. Значит, и уравнение 2х + 5 = 2(х + 6) не имеет корней.

Уравнение З(х + 2) + х = 6 + 4х сводится к уравнению Ох = О, корнем которого является любое число. Следовательно, корнем уравнения З (х + 2) + х = 6 + 4х является любое число.

126. Найдите корень уравнения:
а) 5х = —60; г) 6х = —50;	ж) 0,7х = о;
6) -10х = 8; д) —9х = —3;	з) —1,5х = 6;
е) 0,5х = 1,2; 127. Решите линейное уравнение:	и) 42х = 13.

в) —4х

З7

8' 7
128. Найдите корень уравнения:
а) 5х — 150 = О; г) 12х — 1 = 35; ж) 7 = 6 - 0,2х;
6) 48 - 3х = о; д) —х + 4 = 47; з) 0,15х	51;
в) -1,5х о; е) 1,3х = 54 + х; и) -0,7х 129. Решите уравнение: 1 а) 2х + 9 = 13 - х; ж) 15- Р = б Р- 1; 6) 14 - у = 19 - 11у; 3) з в) о,5а + 11 = 4 - за; и) 2 г) к) х — 4х = О; д) - о,зт = 2 + 1,7т; л) е) 0,8х + 14 = 2 - 1,6х; м) 5у = бу. 130. Решите уравнение:	65.

2 5 2

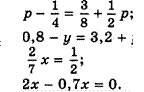а) 3х — 8 = х + 6; д)

6) 7а - 10 = 2 - 4а•,

в) 6¹у - 3 = 3- ^А2 у;

г) 2,6 - 0,2b = - 0,5b•,

131. Найдите корень уравнения:

а) (у + 4) — (у — 1) = бу; в) 6х — (7х — 12) = 101;

г) 20х = 19 - (3 + 12х).

132. Найдите корень уравнения:

а) (13х - 15) - (9 + 6х) = -3х;

6) 12 - (4х - 18) = (36 + 4х) + (18 - бх)•,

в) 1,6х - (х - 2,8) = (0,2х + 1,5) - 0,7;

г) (0,5х + 1,2) - (3,6 - 4,5х) = (4,8 - о,зх) + (10,5х + 0,6).

зо	Глава

133. Решите уравнение:

а) 5х + (3х — З) = 6х + 11; в)

6) За - (10 + ба) = 54; г) 0,6 + (0,5у - 1) = у + 0,5.

134. При каком значении значение выражения 8b — 27 равно: а) 5; б) —11; в) 1,8; г) -1?

135. При каком значении переменной:

а) значения выражений 2m — 13 и т + З равны;

б) значение выражения З — 5с на 1 меньше значения выражения 1 — с;

в) значение выражения 2х + 1 на 20 больше значения выражения 8х + 5;

г) значение х в З раза меньше значения выражения 45 — 10х;

д) значение выражения 9 — у в 2 раза больше значения у?

136. При каком значении у:

а) значения выражений 5у + З и 36 — у равны;

б) значение выражения 7у — 2 больше значения выражения 2у на 10;

в) значение выражения 1,7у + 37 меньше значения выражения 9,3у — 25 на 14?

137. Решите уравнение:

а) 2х + 5 = 2 (х + 1) 11;

6) 5(2у - 4) = 2(5у - 10);

138. Решите уравнение:

а) 15(х + 2) - ЗО = 12х;

в) Зу — (У — 19) = 2у;

г) 6х = 1 — (4 — бх).

в) Зу + (у — 2) = 2(2у - 1);

г) бу — (у —

139. Укажите все целые значения у, при которых верно двойное неравенство:

140. Подберите какое-нибудь число, заключённое между данными числами. Результат запишите в виде двойного неравенства:

а) 7,8 и 7,9;в) —0,3 и —0,4;

141. Отметьте в координатной плоскости точки А (—3; 4), В (6; 5),

142. Упростите выражение и найдите его значение:

а) 6,8с — (3,6с + 2,1) при с = 2,5;

б) 4,4 — (9,6 — 1,2m) при т = —3,5.

8. Решение задач с помощью уравнений

При решении задач с помощью уравнений поступают следующим образом:

обозначают некоторое неизвестное число буквой и, используя условие задачи, составляют уравнение; решают это уравнение; истолковывают полученный результат в соответствии с условием задачи.

Задача 1. В корзине было в 2 раза меньше яблок, чем в ящике. После того как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?

Пусть в корзине было х яблок, тогда в ящике было 2х яблок. После того как из корзины переложили в ящик 10 яблок, в корзине стало х — 10 яблок, а в ящике стало 2х + 10 яблок. По условию задачи в ящике стало в 5 раз больше яблок, чем в корзине. Значит,

- 10) = 2х + 10.

Решим составленное уравнение:

5х - 50 = 2х + 10,

5х - 2х = 10 + 50, 3х = 60, х = 20.

Следовательно, в корзине было 20 яблок.

Так как 2х = 2 • 20 = 40, то в ящике было 40 яблок. Ответ: 20 яблок и 40 яблок.

З а дача 2. Предназначенные для посадки 78 саженцев смородины решили распределить между тремя бригадами так, чтобы первой бригаде досталось саженцев в 2 раза меньше, чем второй, а третьей — на 12 саженцев больше, чем первой. Сколько саженцев надо выделить первой бригаде?

Пусть первой бригаде решили выделить х саженцев. Тогда второй следует выделить 2х саженцев, а третьей х + 12 саженцев. Общее число саженцев х + 2х + (х + 12), что по условию задачи равно 78. Значит:

х + + (х + 12) = 78.

32	Глава

Решим полученное уравнение:

х + 12 = 78,

78 - 12, 4х = 66, х = 16,5.

По смыслу задачи значение х должно быть натуральным ^скислом, а корень уравнения — дробное число. Значит, распределить саженцы указанным способом нельзя.

От в е т: Такое распределение саженцев невозможно. <

143. В одной кассе кинотеатра продали на 36 билетов больше, чем в другой. Сколько билетов продали в каждой кассе, если всего было продано 392 билета?

На Парковой и Молодёжной улицах восстановили разрушенные в половодье 19 домов. На Парковой было восстановлено на З дома меньше, чем на Молодёжной. Сколько домов было восстановлено на каждой из этих улиц?

Периметр треугольника равен 16 см. Две его стороны равны между собой, и каждая из них на 2,9 см больше третьей. Каковы стороны треугольника?

146. Протяжённость автомобильной трассы составляет 6940 м. Большую часть трассы занимают два тоннеля, длина одного из которых на 17 м больше длины другого. Найдите длину каждого тоннеля, если наземная часть трассы составляет 703 м.

147. Старинная заДача. Из четырёх жертвователей второй дал вдвое больше первого, третий — втрое больше второго, четвёртый — вчетверо больше третьего, а все вместе дали 132 рупий. Сколько дал каждый?

148. Двое рабочих изготовили 86 деталей, причём первый изготовил на 1596 деталей больше, чем второй. Сколько деталей изгото-

вил каждый рабочий?

149. Прибыль, полученная фирмой за первые два квартала текущего года, составила 126 ООО р., причём прибыль, полученная во втором квартале, была на 10 ⁰/0 выше, чем в первом. Какую прибыль получила эта фирма в первом квартале?

150. Три школы получили 70 компьютеров. Вторая школа получила на 6 компьютеров больше первой, а третья — на 10 компьютеров больше второй. Сколько компьютеров получила каждая школа?

ё с

Макарычев, 7 кл.

151. На свитер, шапку и шарф израсходовали 555 г шерсти, причём на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?

152. Можно ли расположить 158 книг на трёх полках так, чтобы на первой полке было на 8 книг меньше, чем на второй, и на 5 книг больше, чем на третьей?

153. Можно ли 59 банок консервов разложить в три ящика так, чтобы в третьем было на 9 банок больше, чем в первом, а во втором — на 4 банки меньше, чем в третьем?

154. На одном садовом участке в 5 раз больше кустов малины, чем на другом. После того как с первого участка пересадили на второй 22 куста, на обоих участках кустов малины стало поровну. Сколько кустов малины было на каждом участке?

155. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

156. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2 ч пройдёт столько же, сколько вторая за З ч. С какой скоростью идут автомашины?

157. Старинная задача. Послан человек из Москвы в Вологду и велено ему проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней второй догонит первого?

158. Для ремонта школы прибыла бригада, в которой было в 2,5 раза больше маляров, чем плотников. Вскоре прораб включил в бригаду ещё четырёх маляров, а двух плотников перевёл на другой объект. В результате маляров в бригаде оказалось в 4 раза больше, чем плотников. Сколько маляров и сколько плотников было в бригаде первоначально?

159. (Для работы в парах.) В классе учится ... учащихся. Отношение числа девочек к числу мальчиков равно 5 : 4. Сколько девочек и сколько мальчиков учится в классе?

1) Выясните, какие числа, соответствующие смыслу задачи, можно поставить вместо многоточия.

2) Предложите друг другу закончить решение для одного из найденных чисел.

З) Обсудите полученные ответы.

160. В корзине было в 2 раза меньше винограда, чем в ящике. После того как в корзину добавили 2 кг, в ней стало винограда на 0,5 кг больше, чем в ящике. Сколько винограда было в корзине?

34	Глава

161. Один арбуз на 2 кг легче, чем другой, и в 5 раз легче, чем третий. Первый и третий арбузы вместе в З раза тяжелее, чем второй. Найдите массу каждого арбуза.

162. В двух мешках было по 50 кг сахара. После того как из одного мешка взяли в З раза больше сахара, чем из другого, в нём осталось в 2 раза меньше сахара, чем в другом. Сколько сахара осталось в каждом мешке?

163. Постройте в координатной плоскости точку, у которой:

а) абсцисса равна З, а ордината противоположна абсциссе;

б) абсцисса равна —2, а ордината на единицу больше;

в) абсцисса равна 1,5, а ордината на единицу меньше;

г) абсцисса равна 6, а ордината — противоположному числу.

164. Постройте в координатной плоскости отрезок МА^Т, зная координаты его концов: М (—1; 4) и N(2; —2). Найдите координаты точек пересечения этого отрезка с осью х и с осью у.

165. Найдите значение выражения —0,5 (7b — 12а) — (8,4а — 14b) при а = -10, Ь = -6.

166. Сравните с нулём значение выражения: 17! - 175

З 6

а) -3,52 • 1,7; в) 42 53 д) з 7

6,4- 6?

5 з

6) (-2,88) : (-0,9); г)

8 1

Контрольные вопросы и задания

Сформулируйте определение корня ло 7 корнем уравнения: 6х = 42; Что значит решить уравнение? х — 2х 6=0; 5х — 4х=6 + х.

Какие уравнения называются свойства уравнений. Приведите ного уравнению: 5х — 1 = З; 0,2х = Дайте определение линейного Приведите примеры.

В каком случае уравнение ах = имеет бесконечно много корней; примеры.

уравнения. Является ли чисОх = 11; (16 — 2 • 8) х = 0?

Решите уравнение: 6х = —12;

равносильными? Сформулируйте пример уравнения, равносиль1,1; 3х — 4х + О.

уравнения с одной переменной.

имеет единственный корень; не имеет корней? Приведите

5 с

—1СПф4ЕСКИЕ ХАРАКТЕРИСТИКИ

9, Среднее арифметическое,

размах и мода

При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определённый день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:

23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и сумму разделить на 12:

23 + 18 + 25 + 20 + 25 + 25 + 32 + 37 + 34 + 26 + 34 + 25

- К = 27.

Число 27, полученное в результате, называют среДним арифметическим рассматриваемого ряда чисел.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Мы нашли, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем по 27 мин. Проводя аналогичные наблюдения за этой группой учащихся, можно проследить, какова была средняя затрата времени на выполнение домашнего задания по алгебре в течение недели, сравнить среднюю затрату времени на выполнение в какой-либо день домашних заданий по алгебре и русскому языку и т. п. Заметим, что для серьёзных выводов о загруженности учащихся домашними заданиями необходимо выделить для наблюдений значительно ббльшую группу, чем 12 человек.

Среднее арифметическое представляет собой то значение величины, которое получается, когда сумма всех наблюдаемых значений мысленно распределяется поровну между единицами наблюдения. Например, вычислив среднее арифметическое удоев молока, полученных за сутки на ферме от всех коров, мы найдём тот удой, который получили бы на ферме в эти сутки от одной коровы, если бы все коровы давали одинаковое количество молока, т. е. найдём среднесуточный удой молока на ферме от одной коровы. Аналогично находят среднюю урожайность пшеницы с 1 га в районе, среднюю выработку рабочего бригады за смену и т. п.

36	Глава

Заметим, что иногда вычисление среднего арифметического не даёт полезной информации. Например, нецелесообразно использовать в качестве обобщающего показателя среднюю урожайность зерновых и бахчевых культур в фермерском хозяйстве, средний размер обуви, которую носят учащиеся школы.

В рассмотренном примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 мин. Однако анализ приведённого ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 мин, т. е. от среднего арифметического. Наибольший расход равен 37 мин, а наименьший — 18 мин. Разность между наибольшим и наименьшим расходом времени составляет 19 мин. В этом случае говорят, что размах ряда равен 19.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда находят, когда хотят определить, как велик разброс данных в ряду. Пусть, например, в течение суток отмечали каждый час температуру воздуха в городе. Для полученного ряда данных полезно не только вычислить среднее арифметическое, показывающее, какова среднесуточная температура, но и найти размах ряда, характеризующий колебание температуры воздуха в течение этих суток.

При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, т. е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 — моДа рассматриваемого ряда.

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Например, в ряду чисел

47, 46, 50, 52, 47, 52, 49, 45, 43, 53, 53, 47, 52

две моды — это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа — менее трёх раз.

В ряду чисел

69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72

моды нет.

Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Например, если изучаются данные о размерах мужских сорочек, проданных в определённый день в универмаге, то удобно воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом. Среднее арифметическое в этом случае не даёт полезной информации. Мода является наиболее приемлемым показателем при выявлении расфасовки некоторого товара, которой отдают предпочтение покупатели, цены на товар данного вида, распространённой на рынке, и т. п.

Рассмотрим ещё пример. Пусть, проведя учёт деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:

36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.

Найдём для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упоряДоченный ряд чисел, т. е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим

35, 35, 36, 36, 36, 36, 36, 36, 36, 36,

37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.

Вычислим среднее арифметическое:

35 - 2 + 36 - 8 + 37 - 4 + 38 , 3 + 39 . 4 776

37.

21 21

Размах ряда равен 39 — 35 = 4. Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.

Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит 4 деталей; типичной является выработка, равная 36 деталям.

Среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда, а мода, если она существует, обязательно совпадает с двумя или более числами ряда. Кроме того, в отличие от среднего арифметического понятие «мода» относится не только к числовым данным. Например, проведя опрос учащихся, можно получить ряд данных, показывающих, каким видом спорта они предпочитают заниматься, какую из развлекательных телевизионных программ они считают наиболее интересной. Модой будут служить те ответы, которые встречаются чаще всего. Этим и объясняется само название «мода».

38	Глава

Такие характеристики, как среднее арифметическое, размах и мода, находят применение в статистике — науке, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и её регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т. п. Результаты статистических исследований широко используются для практических и научных выводов.

167. Найдите среднее арифметическое и размах ряда чисел:

а) 24, 22, 27, 20, 16, 31; в) 15, 17, 19, 25, 17, 15; 6) 30, 5, 23, 5, 28, 30; г) 40, 35, 30, 25, 30, 35.

168. Найдите среднее арифметическое, размах и моду ряда чисел:

а) 32, 26, 18, 26, 15, 21, 26; 6) 21, 18,5, 25,3, 18,5, 17,9;

в) 67,1, 68,2, 67,1, 70,4, 68,2;

г) 0,6, 0,8, 0,5, 0,9, 1,1.

169. Найдите среднее арифметическое, размах и моду ряда чисел:

а) 16, 22, 16, 13, 20, 17; 6) -21, -33, -35, -19, -20, -22;

в) 61, 64, 64, 83, 61, 71, 70;

г) -4, -6, о, 4, о, 6, 8, -12.

170. Как могут измениться размах и мода ряда чисел, если: а) дополнить его числом, превосходящим все остальные;

б) вычеркнуть из него число, меньшее всех остальных;

в) дополнить его числом, равным наибольшему из чисел?

171. В таблице показан расход электроэнергии некоторой семьёй в течение года:

Месяц		п	Ш	IV	V	VI		ШП		Х		ХП
Расход электроэнергии, кВт-ч	85	80	74	61	54	34	32	32	62	78	81	82

Найдите средний ежемесячный расход электроэнергии этой семьёй.

172. В таблице приведены данные о продаже в течение недели картофеля, завезённого в овощную палатку:

День недели			ср
Количество картофеля, кг	275	286	250	290	296	315	325

Сколько картофеля в среднем продавали ежедневно в эту неделю?

[ij$)] Среднее арифметическое ряда, состоящего из десяти чисел, равно 15. К этому ряду приписали число 37. Чему равно среднее арифметическое нового ряда чисел?

[(?4] Среднее арифметическое ряда, состоящего из девяти чисел, равно 13. Из этого ряда вычеркнули число З. Чему равно среднее арифметическое нового ряда чисел?

В ряду чисел 2, 7, 10, 18, 19, 27 одно число оказалось стёртым. Восстановите его, зная, что среднее арифметическое этого ряда чисел равно 14.

(Для работы в парах.) В ряду чисел З, 8, 15, 30, , 24 пропущено одно число. Найдите его, если:

а) среднее арифметическое ряда равно 18;

б) размах ряда равен 40.

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

2) Проверьте друг у друга правильность выполнения задания. З) Обсудите, почему в задании б) получаются два ответа.

177. В таблице показано число деталей, изготовленных за смену рабочими одной бригады:

п/п

Фамилия

Число деталей

2 З

Иванов

Лазарев

Ильин

Бережной

Егоров Петров

Семёнов Лукин Андреев

Попов

Сурков

Для представленного в таблице ряда чисел найдите среднее арифметическое, размах и моду. Каков смысл каждого из этих показателей?

40	Глава I

178. На соревнованиях по фигурному катанию выступление спортсмена было оценено следующими баллами:

5,2, 5,4, 5,5, 5,4, 5,1, 5,1, 5,4, 5,5, 5,3.

Для полученного ряда чисел найдите среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?

179. В аттестате о среднем образовании у четырёх друзей — выпускников школы — оказались следующие оценки:

Ильин: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;

Семёнов: З, 4, З, З, З, З, 4, З, З, З, З, 4, 4, 5, 4; Попов: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;

Романов: З, З, 4, 4, 4, 4, 4, З, 4, 4, 4, 5, З, 4, 4.

С каким средним баллом окончил школу каждый из друзей? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характеристики вы использовали при ответе?

180. В фермерском хозяйстве отведены под пшеницу три участка, площади которых равны 12 га, 8 га и 6 га. Средняя урожайность на первом участке составляет 18 ц с 1 га, на втором 19 ц с 1 га, на третьем — 23 ц с 1 га. Чему равна средняя урожайность пшеницы в этом хозяйстве? Можно ли найти среднюю урожайность пшеницы, вычислив среднее арифметическое чисел 18, 19 и 23?

181. Проведя учёт числа бракованных деталей в 10 ящиках с одинаковым числом деталей, получили следующий ряд данных:

Найдите для этого ряда среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?

182. Каждый из 24 участников соревнований по стрельбе произвёл по десять выстрелов. Отмечая всякий раз число попаданий в цель, получили следующий ряд данных:

Найдите для этого ряда размах и моду. Что характеризует каждый из этих показателей?

183. В таблице записаны результаты ежедневного измерения в полдень температуры воздуха в течение первой декады марта:

Число месяца	1	2	з	4	5	6	7	8	9	10
Температура, ^ос	-2	-1	-3	О	1	2	2	з	4	з

Найдите среднюю температуру в полдень в эту декаду. Составьте таблицу отклонений от средней температуры воздуха в полдень в каждый из дней декады.

184. (ЗаДача-исслеДование.) Средний возраст сотрудников отдела компьютерной вёрстки, в котором работали 12 человек, составлял 30,5 года. После того как из отдела уволился двадцатилетний Олег и на его место пришёл Игорь, средний возраст сотрудников отдела стал составлять 31 год. Сколько лет Игорю?

1) Выскажите предположение о возрасте Игоря.

2) Найдите первоначальную сумму возрастов сотрудников отдела.

З) Обозначив возраст Игоря через х (лет), найдите какой стала сумма возрастов сотрудников отдела.

4) Выразите через х, каким стал средний возраст сотрудников отдела.

5) Составьте уравнение и решите его.

6) Подтвердилось ли ваше предположение о возрасте Игоря?

185. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал на 2096 больше, чем в первый, а в третий на 24 страницы больше, чем во второй. Сколько страниц прочитал ученик в первый день?

1 0. Медиана как статистическая

характеристика

Рассмотрим ещё одну статистическую характеристику.

Начнём с примера. В таблице показан расход электроэнергии в январе жильцами девяти квартир:

Номер квартиры	1	2	8	4	5	6		8	9
Расход электроэнергии, кВт • ч	85	64	78	93	72	91	72	75	82

Составим из данных, приведённых в таблице, упорядоченный ряд: 64, 72, 72, 75, 82, 85, 91, 93.

В полученном упорядоченном ряду девять чисел. Нетрудно заметить, что в середине ряда расположено число 78: слева от него записано четыре числа и справа четыре числа.

Говорят, что число 78 является срединным числом, или, иначе, медианой, рассматриваемого упорядоченного ряда чисел (от латинского слова mediana, которое означает «среднее»). Это число считают также медианой исходного ряда данных.

42	Глава

Приведём теперь другой пример. Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам добавили ещё десятую. Получили такую таблицу:

Номер квартиры	1	2	з	4	5	6	7	8	9	10
Расход электро- энергии, кВт • ч	85	64	78	93	72	91	72	75	82	83

Так же как в первом случае, представим полученные данные в виде упорядоченного ряда чисел:

64, 72, 72, 75, 78, 83, 85, 91, 93.

В этом числовом ряду чётное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдём среднее арифмети-

78 + 82 ческое этих чисел: = 80. Число 80, не являясь членом ряда, 2 разбивает этот ряд на две одинаковые по численности группы — слева от него находятся пять членов ряда и справа тоже пять членов ряда:

80

64, 72, 72, 75, 78, 82, 83, 85, 91, 93.

Говорят, что медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Если в упорядоченном числовом ряду содержится 2n — 1 членов, то медианой ряда является п-й член, так как п — 1 членов стоит до п-го члена и п — 1 членов — после п-го члена. Если в упорядоченном числовом ряду содержится 2n членов, то медианой является среднее арифметическое членов, стоящих на п-м и п + 1-м местах.

В каждом из рассмотренных выше примеров, определив медиану, мы можем указать номера квартир, для которых расход электроэнергии жильцами превосходит срединное значение, т. е. медиану.

Рассмотрим ещё пример. Известно, что 34 сотрудника отдела приобрели акции некоторого акционерного общества. Данные о числе акций, приобретённых сотрудниками, представлены в виде следующего упорядоченного ряда:

4, 100.

12 раз 16 раз

Найдём медиану этого ряда. Так как всего в ряду 34 числа, то медиана равна среднему арифметическому 17-го и 18-го членов, т. е. равна

Вычисляя среднее арифметическое этого ряда, найдём, что оно приближённо равно 6,2, т. е. в среднем сотрудники отдела приобрели примерно по 6 акций.

Мы видим, что в данном случае медиана лучше отражает реальную ситуацию, так как половину всех сотрудников составляют те, которые приобрели не более З акциЙ.

Вообще среднее арифметическое зависит от значений всех членов в упорядоченном ряду данных, в том числе и от значений крайних членов, которые часто бывают наименее характерными для рассматриваемой совокупности данных. Поэтому при анализе данных сведения о среднем арифметическом часто дополняются указанием медианы.

Такие показатели, как среднее арифметическое, мода и медиана, по-разному характеризуют данные, полученные в результате наблюдений. Поэтому на практике при анализе данных в зависимости от конкретной ситуации используют какой-либо из этих показателей, либо два из них, либо даже все три.

186. Найдите медиану ряда чисел:

а) 30, 32, 37, 40, 41, 42, 45, 49, 52; 6) 102, 104, 205, 207, 327, 408, 417;

в) 16, 18, 20, 22, 24, 26;

г) 1,2, 1,4, 2,2, 2,6, 3,2, 3,8, 4,4, 5,6.

187. Найдите среднее арифметическое и медиану ряда чисел:

а) 3,8, 7,2, 6,4, 6,8, 7,2; 6) 21,6, 37,3, 16,4, 12,6.

188. Известно, что ряд данных состоит из натуральных чисел. может ли для этого ряда быть дробным числом:

а) среднее арифметическое; в) размах;

б) мода; г) медиана?

	Глава

189. В таблице показано число изделий, изготовленных за месяц членами бригады:

п/п

Фамилия

Число изделий

п/п

Фамилия

Число изделий

1 2 з

Антонов

Астафьев Баранов

Бобков

Васильев

Егоров

185

194

179

185

136

158

Квитко

Лазарев

Осокин

Рылов

Сухов

178

149

156

185

168

Найдите медиану этого ряда данных. У кого из членов бригады выработка за месяц была больше медианы?

190. В таблице показано, сколько акций одинаковой стоимости некоторого акционерного общества приобрели сотрудники отдела:

п/п

Фамилия

Число акций

п/п

Фамилия

Число акций

1 2 з 4

Астахова

Бодров

Волков

Ерин

Ильин Куликова

Лаврова

Михайлов

4 10 з 2

10 25

Муравьёв Николаева

Осипов

Павлов

Петрова

Райков Тимофеев

Фёдоров

Найдите медиану этого ряда данных. У кого из сотрудников отдела число приобретённых акций не превосходит медиану?

191. Подсчитав число сорных семян в 15 пакетиках с семенами, получили такие данные:

Для представленного ряда данных найдите среднее арифметическое и медиану. Что характеризует каждый из этих показателей?

192. Отмечая время (с точностью до минуты), которое токари бригады затратили на обработку одной детали, получили ряд данных:

30, 32, 32, 38, 36, 31, 32, 38, 35, 36, 32, 40, 42, 36, 33, 35, 32, 32, 40, 38.

Для полученного ряда данных найдите размах, моду и медиану. Объясните практический смысл этих показателей.

193. В организации вели ежедневный учёт поступивших в течение месяца писем. В результате получили такой ряд данных:

39, 43, 40, о, 56, 38, 24, 21, 35, 38, о, 58, 31, 49, 38, 25, 34, о, 52, 40, 42, 40, 39, 54, о, 64, 44, 50, 38, 37, 32.

Для полученного ряда данных найдите среднее арифметическое, размах, моду и медиану. Каков практический смысл этих показателей?

194. Сравните значения выражений 12а — 56 и 8а — 2b при а —- -3,5,

195. Решите уравнение:

а) б(у - 1) = 9,4 - 1,7у; 6) - 2,7т + 3,2.

Контрольные вопросы и задания

ряда чисел? Может ли не совпадать ни с одним из

Что называется средним арифметическим среднее арифметическое ряда чисел ряда?

Что называется размахом ряда

Что называется модой ряда чисел? моду? Может ли ряд чисел иметь мода ряда чисел не совпадать ни что называется медианой ряда чисел не совпадать ни с одним из ется медианой упорядоченного 2п чисел?

чисел?

Любой ли ряд чисел имеет более одной моды? Может ли с одним из чисел ряда?

чисел? Может ли медиана ряда чисел ряда? Какое число являряда, содержащего 2п — 1 чисел?

Для тех, кто хочет знать больше

1 1 , Формулы

В художественной литературе вам, вероятно, приходилось встречаться с непривычными единицами измерения. Так, например, в книге Жюля Верна «Дети капитана Гранта» читаем:

«Это был ябиру — гигантский журавль английских колоний. Эта птица пяти футов ростом, с чёрным широким клювом конической формы, заостряющимся к концу, в длину он имел восемнадцать дюймов»;

	Глава

«Во время пробного плавания яхта «Дункан» показала скорость в семнадцать морских миль в час»;

«Роберт узнал, что средняя годовая температура в провинции Виктория достигает +74 ⁰по Фаренгейту» .

Для того чтобы этот текст был понятен, надо знать, как упомянутые здесь единицы измерения, выражающие приближённые значения величин, соотносятся с привычными для вас единицами.

Это соотношение выражается следующими формулами:

Ь = 30,48а, где а — длина в футах, Ь — соответствующая длина в сантиметрах;

I = 2,54m, где т — длина в дюймах, I — длина в сантиметрах; р = 1,853m, где т — расстояние в морских милях, р — расстояние в километрах;

- 32)

, где — температура в градусах Фаренгейта, с

9 температура в градусах Цельсия.

Выполнив расчёты, найдём, что в приведённом тексте ь = 30,48 • 5 = 152 (см); 1,853 • 17 32 (км); 5(74- 32)

! = 2,54 • 18 46 (см); 230.

Заметим, что при выполнении вычислений удобно пользоваться калькулятором.

Значит, в книге Жюля Верна речь идёт о следующих приближённых значениях величин. Высота журавля равна 1,5 м, а длина его клюва — 0,5 м. Яхта «Дункан» шла со скоростью 32 км/ч, а среднегодовая температура в провинции Виктория была равна 23 ⁰Цельсия.

Приведём пример использования формул в задаче на проценты.

Пример 1, Найдём, на сколько процентов увеличится площадь прямоугольника, если его длину и ширину увеличить на 10 ⁰/0 .

Пусть длина прямоугольника равна а см, ширина — Ь см, а площадь — S см ².

По формуле площади прямоугольника находим, что S = ab. После увеличения длины и ширины прямоугольника на 10 ⁰/0 длина будет равна а + 0,1а = 1,1а см, а ширина Ь + 0,16 = 1,1b см. Тогда площадь будет равна 1,1а • 1,16 = 1,21ab см ², т. е. увели-

чится на

1,21ab — ab = 0,21ab см ².

0,21аЬ

Имеем 1000/о = 2196. Значит, площадь увеличится

ab на 2196.

Для тех, кто хочет знать больше











	4+3,4:

Этот ответ хорошо поясняет рисунок 6. Из рисунка видно, что к имеющимся 100 малым прямоугольникам, площадь каждого из которых составляет 1 % от площади прямоугольника, добавляется ещё 21 малый прямоугольник.

Свойства равенств позволяют из одной формулы, связывающей две или более переменные, получать новые формулы.

Пример 2. Из формулы с = , где f температура в граду9 сах Фаренгейта, с — температура в градусах Цельсия, выразим переменную ,f через с.

- 32)

Умножив обе части равенства с = на 9, получим 9

9с 5(f - 32).

Отсюда

9с = 5f - 160, 9с + 160.

9с + 160

Значит, = , т. е. + 32.

Мы получили формулу, позволяющую переходить от температуры в градусах Цельсия к температуре в градусах Фаренгейта.

196. Пользуясь формулой Ь = 1,067а, где а — расстояние в вёрстах, Ь — расстояние в километрах, выразите в километрах расстояние, равное:

а) 6 верстам; б) 12,5 версты; в) 104 верстам.

197. Выразите в килограммах массу, равную З пудам, 20,5 пуда, воспользовавшись формулой р = 16,38m, где т — масса в пудах, р — масса в килограммах.

198. Пользуясь формулой с = 0,454f, где f — масса в фунтах, с — масса в килограммах, выразите в килограммах массу, равную:

а) 8 фунтам; б) 30,5 фунта.

Как изменится площадь прямоугольника, если:

а) его длину и ширину уменьшить на 10 ⁰/0 ;

б) его длину увеличить на 30 ⁰/0 , а ширину уменьшить на 30 ⁰/0 ?

48	Глава

Как изменится объём куба, если длину его ребра увеличить на 20 ⁰/0 ?

Цену на товар сначала повысили на 1596, а затем снизили на 15 ⁰/0 , так как товар перестал пользоваться спросом. Первоначальная цена товара составляла а р., а окончательная Сравните числа а и Ь (выберите верный ответ).

4. Сравнить нельзя, так как неизвестно значение а

На распродаже цену на костюм снизили на 20 ⁰/0 . На сколько процентов надо повысить новую цену, чтобы вернуться к первоначальной?

Найдите:

а) какой температуре по Фаренгейту соответствует 4 ^ос; —15 ^ос;

б) какой температуре по Цельсию соответствует 20 ⁰F; —16 ⁰F;

Может ли температура быть:

а) положительной по Цельсию и отрицательной по Фаренгейту;

б) положительной по Фаренгейту и отрицательной по Цельсию?

Выразите из формулы:

а) s = at переменную t; • h переменную Ь.

б) = (...'o + at переменную а;

упражнения к главе

К параграфу 1

206. Найдите число, обратное:
2 а) сумме чисел — и —	1 1 в) произведению чисел
3'	15 16'
б) разности чисел 6,2 и 5,8;	г) частному чисел 4,9 и 3,5.

207. Найдите число, противоположное:

а) сумме чисел 2,86 и —4,3;

4 5

б) разности чисел — 96'

в) произведению чисел —5,75 и 1,6;

2 г) частному чисел 46 и —7 —.

Найдите сумму всех целых чисел от —102 до 104.

Найдите произведение всех целых чисел от —11 до 13.

210. Найдите значение выражения:

1 20 4- 1

а) при т = — б) при а = 3,5.

3 '

Известно, что при некоторых значениях а и Ь значение выражения 2 (а + Ь) равно —8,1. Найдите при тех же значениях а и Ь значение выражения:

в) 4а + 4b; г) —5а — 5b.

212 • При каких значениях переменных не имеет смысла выражение: 5 З

а) ' б) в) г) 2х - 4

213. Составьте выражение для решения задачи:

а) Периметр прямоугольника 16 см, одна из его сторон т см. Какова площадь прямоугольника?

б) Площадь прямоугольника 28 м ², а одна из его сторон равна а м. Чему равен периметр прямоугольника?

Из двух городов, расстояние между которыми 8 км, навстречу друг другу одновременно выехали два автомобиля. Скорость одного из них км/ч, а скорость другого км/ч. Через сколько часов они встретятся?

Через какое время мотоциклист догонит велосипедиста, если расстояние между ними 8 км, скорость велосипедиста 1.91 км/ч, а скорость мотоциклиста 1.92 км/ч?

От прямоугольного листа картона со сторонами а см и Ь см отрезали по углам квадраты со сторонами х см (рис. 7). Из оставшейся части сделали открытую коробку. Запишите формулу для вычисления объёма V коробки. Вычислите по формуле объём коробки, если а = 35, Ь = 25, х = 5. Какие значения может принимать переменная х при указанных значениях а и Ь?

50	Глава

215. Составьте формулу числа: а) кратного 11; б) кратного 21.

216. Чтобы выразить в километрах расстояние, измеренное в морских милях, пользуются формулой у = 1,853х, где х — расстояние в милях, а у — то же расстояние в километрах. Выразите в километрах следующие расстояния: 10 миль, 50 миль, 250 миль.

217. Сравните:
а) 3,48 - 4,52 и -8,93 + 0,16;	в) 4,7 - 9,65 и
1 6) 6,48 и 6,48 : ²;	З г) • 16,4 и 16,4 • З
8 8	4

218. Верно ли, что:

а) если а > О и Ь > О, то ab > О;

б) если ab > О, то а и b > О?

Верно ли, что для любых чисел а и Ь:

б) labl = а 1 •

Известно, что lxl = lyl. Верно ли, что х = у?

221.] Известно, что lal < lbl. Верно ли, что а < Ь?

[Д] Известно, что lal > lbl. Возможно ли, чтобы было а < Ь?

К параграфу 2

223. Найдите значение выражения:

а) 5,9 • + • + • 4,1; 6) 6,8 • - • + • 1,6. [ЦБ] Вычислите:

а) (1,25 • • 0,8 - 1,7) • 3,45; 6) 3,947 : (3,6 - • 4 0,25).

Ц] Объясните, почему равенство является тождеством:

[Ц Является ли тождеством равенство:

б) la ²+ 41 = а ²+ 4;

227. Докажите, что:

а) если к сумме двух чисел прибавить их разность, то получится удвоенное первое число; б) если из суммы двух чисел вычесть их разность, то получится удвоенное второе число.

228. Докажите, что выражение тождественно равно нулю:

а) (а + Ь) х + (а — Ь) х — 2ах; б) 8(х — у) + 8(у — х).

229. Докажите, что:

а) выражение х (—1) + х (—2) + х (—3) + 6х тождественно равно нулю;

б) выражение а (—5)+а• тождественно равно —2а.

230. Найдите значение выражения 8а — (4b + За) — (4а — 3b):

а) при а = 6,8, Ь = 7,3; б) при а 8,9, Ь

231. Докажите, что значение выражения не зависит от а:

а) а + (20 - (За - б) а — (ба — (5а — 8)).

232. Докажите, что если одно из чисел кратно З, а другое кратно 5, то их произведение кратно 15.

К параграфу З

233. Является ли корнем уравнения (2х — 3,8) (4,2 + 3х) = О число: а) 1,9;

234. Какие из чисел —4, —3, —1, З, 4 являются корнями уравнения:

52	Глава

а) х ²+ 4х + З = О; 6) х ²+ х = 12?

235. Имеет ли корни уравнение:

в) х ²= х;

236. Почему не имеет корней уравнение:

а) 1х1 = -1; 6) lxl + 3 = O?

[П] Решите уравнение:

Р$$З При каких значениях коэффициента т уравнение тх = 5 имеег единственный корень? Существует ли такое значение т, при котором это уравнение не имеет корней? имеет бесконечно много корней?

При каких значениях коэффициента р уравнение рх = 10 имеет корень, равный —5; 1; 20?

240. Решите уравнение:

а) 3,8х - (1,6 - 1,2х) = 9,6 + (3,7 - 5х)•, 6) (4,5у + 9) - (6,2 - езду) = 7,2у + 2,8;

в) о,бт - 1,4 (3,5т + 1,7) - (2,7т - 3,4);

г) (5,30 - 0,8) - (1,6 - 4,70) = 20 - (а - 0,3).

241. Решите уравнение:

д) х (х + З)(х + З) = О;

в) (х — 11)(х + 6) = О; е) (Х — 4) (Х + 9) (Х + 13) = О.

Может ли иметь положительный корень уравнение: 6) + 3х + 1 = 0? 243. Решите уравнение:

а) - 4) = 9,9 - - 1);

в) (0,7х - 2,1) - (0,5 - 2х) = - 1) + 0,1;

г) -3(2 - о,4у) + 5,6 = + 1).

244. При каком значении переменной:

а) сумма выражений 2х + 7 и —х + 12 равна 14;

б) разность выражений —5у + 1 и Зу + 2 равна —9;

в) сумма выражений 15х — 1 и 6х — 8 равна их разности;

г) разность выражений 25р + 1 и р — 12 равна их сумме?

245. Найдите все целые значения а, при которых корень уравнения ах = 6 является целым числом.

Не решая уравнения 7 (2х + 1) = 13, докажите, что его корень не является целым числом.

247. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько кур на ферме?

248. На первом участке было посажено на 9 кустов смородины больше, чем на втором. Если со второго участка пересадить на первый З куста, то на первом участке станет в 1,5 раза больше кустов смородины, чем на втором. Сколько кустов смородины на первом участке?

249. У Миши в 4 раза больше марок, чем у Андрея. Если Миша отдаст Андрею 8 марок, то у него станет марок вдвое больше, чем у Андрея. Сколько марок у каждого мальчика?

250. Чтобы сдать в срок книгу в библиотеку, ученик должен был читать ежедневно по 40 страниц, но он читал в день на 15 страниц меньше и сдал книгу на 6 дней позже срока. За сколько дней ученик должен был прочитать книгу?

251. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и, благодаря этому, выполнила заказ на З дня раньше срока. Каков был срок выполнения заказа?

252. Если к задуманному числу прибавить 7, полученную сумму умножить на З и из произведения вычесть 47, то получится задуманное число. Какое число задумано?

К параграфу 4

Среднее арифметическое некоторого ряда данных, состоящего из 10 чисел, равно 7. К этому ряду приписали числа 17 и 18. Чему равно среднее арифметическое нового ряда чисел?

254. Сколько чисел в ряду, если его медианой служит:

а) пятнадцатый член ряда;

б) среднее арифметическое семнадцатого и восемнадцатого членов ряда?

В ряду чисел

12,7, 15, 20

54	Глава

пропущены два числа, одно из которых вдвое больше другого. Найдите эти числа, если известно, что среднее арифметическое ряда равно 13.

В ряду чисел

8, 16, 26, , 48, , 46

два числа оказались стёртыми. Найдите эти числа, если известно, что одно из них на 20 больше другого, а среднее арифметическое этого ряда чисел равно 32.

В ряду данных, состоящем из 12 чисел, наибольшее число увеличили на 6. Изменится ли при этом и как: а) среднее арифметическое; в) мода;

б) размах; г) медиана?

В этой главе вы узнаете, что называется функцией и графиком функции. С этими понятиями вы постоянно будете встречаться не только на уроках математики, но и на уроках физики, химии, информатики. Вы узнаете, что с помощью графиков можно получить наглядные представления о свойствах функций, познакомитесь со свойствами линейной функции и её частного вида, прямой пропорциональности. Вас, безусловно, заинтересует возможность использования компьютера при решении некоторых задач, связанных с понятиями функции и графика функции. Вы узнаете, что на практике для вычерчивания графиков различных функций часто используются специальные приборы. Например, с помощью кардиографа получают графическое описание работы сердца, а с помощью сейсмографа — графическое описание колебаний земной поверхности.

ФУНКЦИИ И ИХ ГРАФИКИ

1 2. Что такое функция

На практике мы часто встречаемся с зависимостями между различными величинами. Например, площадь круга зависит от его радиуса, масса металлического бруска зависит от его объёма и плотности металла, объём прямоугольного параллелепипеда зависит от его длины, ширины и высоты.

В дальнейшем мы будем изучать зависимость между двумя величинами.

Рассмотрим примеры.

Пример 1. Площадь квадрата зависит от длины его стороны. Пусть сторона квадрата равна а см, а его площадь равна S см ². Для каждого значения переменной а можно найти соответствующее ему значение переменной S. Так, например: если а = З, то S = 3²= 9; если а = 15, то S = 15 ²= 225; если а = 0,08, то S = 0,08 ²= 0,0064.

5 5.

Зависимость переменной S от переменной а выражается формулой

(по смыслу задачи а > О).

Переменную а, значения которой выбираются произвольно, называют независимой переменной, а переменную S, значения которой определяются выбранными значениями а, называют зависимой переменной.

При мер 2. Путь, пройденный автомобилем со скоростью 50 км/ч, зависит от времени движения.

Обозначим время движения автомобиля (в часах) буквой t, а пройденный путь (в километрах) буквой s. Для каждого значения переменной t, где t О, можно найти соответствующее значение переменной s. Например: если t = 0,5, то s = 50 • 0,5 = 25; если t = 2, то s = 50 • 2 = 100; если t = 3,5, то s = 50 • 3,5 = 175. Зависимость переменной s от переменной t выражается формулой S = 50t.

В этом примере t является независимой переменной, а s — зависимой переменной.

Пр имер З. На рисунке 8 изображён график температуры воздуха в течение суток.

С помощью этого графика для каждого момента времени t (в часах), где О t 24, можно найти соответствующую температуРУ р (в градусах Цельсия). Например: если t = 7, то р = —4; если t —— 12, то р если t 17, то р = З; если t = 22, то р —- 0.

Здесь t является независимой переменной, а р — зависимой переменной.

56	Глава ll

П р имер 4. Стоимость проезда в пригородном поезде зависит от номера зоны, к которой относится станция. Эта зависимость для некоторого региона показана в таблице (буквой п обозначен номер зоны, а буквой т — соответствующая стоимость проезда в рублях):

	1	2	з	4	5	6	7	8	9
	10	10	18	24	зо	36	42	48	54

По этой таблице для каждого значения п, где п — 9, можно найти соответствующее значение т. Так, если п = 2, то т = 10; если п = 6, то т = 36; если п = 9, то т = 54.

В этом случае п является независимой переменной, а т — зависимой переменной.

В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называют функциональной зависимостью или функцией.

Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией от этого аргумента. Так, площадь квадрата является функцией от длины его стороны; путь, пройденный автомобилем с постоянной скоростью, является функцией от времени движения. Значения зависимой переменной называют значениями функции.

Все значения, которые принимает независимая переменная, образуют область определения функции.

Например, область определения функции в примере 1 состоит из всех положительных чисел, а в примере З — из всех чисел от О до 24.

258. Площадь прямоугольника со сторонами 9 см и х см равна S см ². Выразите формулой зависимость S от х. Для значения аргумента х = 4; 6,5; 15 найдите соответствующее значение

функции S.

259. Поезд, двигаясь со скоростью 70 км/ч, проходит за t ч расстояние s км. Задайте формулой зависимость s от t. Найдите значение функции, соответствующее значению аргумента, равному 2,4; 3,8.

ё 5.

260. Объём куба зависит от длины его ребра. Пусть а см — длина ребра куба, а V см ^з— его объём. Задайте формулой зависимость от а. Возьмите два каких-либо значения аргумента и вычислите соответствующие им значения функции.

261. По озеру плавала яхта. Расстояние s (в километрах), на которое удалялась яхта от базы, менялось с течением времени движения t (в минутах). Изменение s в зависимости от t показано на рисунке 9. На каком расстоянии от базы находилась яхта через 20 мин? через 1 ч 20 мин? через 2 ч 30 мин? Какова область определения рассматриваемой функции?

Рис. 9

262. На рисунке 10 показано изменение высоты сосны у (в метрах) в зависимости от её возраста х (в годах). Найдите:

а) высоту сосны в возрасте 10; 40; 90; 120 лет;

б) на сколько выросла сосна за промежуток времени от 20 до 60 лет; от 60 до 100 лет.

Глава ll

263. Каждому натуральному числу п ставится в соответствие остаток r от деления этого числа на 4. Найдите r, если п равно 13, 34, 43, 100. В рассматриваемой функциональной зависимости укажите аргумент. Какова область определения этой функции? Какие числа служат значениями функции?

264. В таблице, составленной в результате измерений, показана зависимость атмосферного давления р (в миллиметрах ртутного столба) от высоты (в километрах):

h, км			1	2	З	4	5
р, мм РТ. ст.	760,0	716,0	614,0	596,7	525,7	462,2	404,8

Каково атмосферное давление на высоте 1 км? 4 км?

На какой высоте атмосферное давление равно 596,7 мм РТ. ст.? 404,8 ММ РТ. СТ.?

265. В одном резервуаре 380 м^зводы, а в другом 1500 м^з. В первый резервуар каждый час поступает 80 м ⁵воды, а из второго каждый час выкачивают 60 м ^з. Через сколько часов воды в резервуарах станет поровну?

266. Отметьте точки А (4; —3) и В (—2; 6). Проведите прямую АВ и найдите координаты точек пересечения этой прямой с осью х и осью у.

13. Вычисление значений функции по формуле

Функции, которые мы рассматривали в предыдущем пункте, задавались различными способами. Наиболее распространённым способом является задание функции с помощью формулы, Формула позволяет для любого значения аргумента находить соответствующее значение функции путём вычислений.

Пример 1. Пусть функция задана формулой 3х-1

, где —3 х < З.

Найдём значения у, соответствующие целым значениям х:

если х = — З , то у =

если х = —2, т¹= —3,5 и т 2

5 5.

Результаты вычислений удобно записать в виде таблицы, поместив в верхней строке значения аргумента, а в нижней строке соответствующие значения функции:

	-3	-2	-1		1	2	з
	-5	-3,5	-2	-0,5	1	2,5	4

Мы выбирали каждый раз значение х на 1 больше предыдущего. Говорят, что мы составили таблицу значений функции с шагом 1.

В рассмотренном примере была указана область определения функции.

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Например, область определения функции, заданной формулой у = х(х + 5), состоит из всех чисел, а область определения функции,

заданной формулой у = , состоит из всех чисел, кроме числа 2.

С помощью формулы, задающей функцию, решают также задачу отыскания значений аргумента, которым соответствует данное значение функции.

Пример 2. Функция задана формулой у = 12х — 3,6. Найдём, при каком значении х значение функции равно 2,4.

Подставим в формулу у = 12х — 3,6 вместо у число 2,4. Получим уравнение с переменной х:

= 12х - 3,6.

Решив его, найдём, что х = 0,5. Значит, у = 2,4 при х = 0,5.

Заметим, что мы смогли решить эту задачу, так как она свелась к уравнению, способ решения которого нам известен.

ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646—1716) — не мецкий философ, математик, физик и языковед. Он и английский учёный И. Ньютон создали (независимо друг от друга) основы важного раздела математики — математического анализа. Лейбниц ввёл многие понятия и символы, употребляемые в математике и сейчас, в частности им введён термин «функция».

60	Глава lI

267. Функция задана формулой у = 2х + 7. Найдите значение функции, соответствующее значению аргумента, равному 1; —20; 43.

2$?. Функция задана формулой у = 0,1х + 5. Для значения аргумента, равного 10; 50; 120, найдите соответствующее значение функции.

269. Функция задана формулой у = В таблице указаны некото-

х рые значения аргумента. Заполните таблицу, вычислив соответствующие значения функции:

	—6	—3	2		5	6	12

270. Функция задана формулой у —				9. Заполните таблицу:
х	—5	-3			2	з	6

271. Составьте таблицу значений функции, заданной формулой у = х(х — 3,5), где х 4, с шагом 0,5.

272. Найдите область определения функции, заданной формулой:

ИТ Формула у = —5х + 6 задаёт некоторую функцию. При каком значении аргумента значение функции равно 6? 8? 100?

2 274. Функция задана формулой у = — х. Заполните пустые клетки з таблицы:

х	—0,5				9
		-2

275. Функция задана формулой у = 0,3х — 6. Найдите значение аргумента, при котором значение функции равно —6; —3; О.

276. Задайте формулой зависимость массы куска пробки от его объёма, если известно, что плотность пробки равна 0,18 г/см ^зНайдите по формуле:

а) массу куска пробки, объём которого равен 240 см^з;

б) объём куска пробки, масса которого равна 64,8 г.

ё 5.

277. Двигаясь со скоростью v км/ч в течение 6 ч, автомобиль прошёл путь s км. Задайте формулой зависимость s от v. Пользуясь этой формулой:

а) найдите s, если = 65; б) найдите v, если s = 363.

278. С турбазы на станцию, удалённую на расстояние 60 км, отправился велосипедист со скоростью 12 км/ч. Задайте формулой зависимость переменной s от переменной t, где s — расстояние велосипедиста до станции (в километрах), а t — время его движения (в часах). Найдите по формуле:

а) 8, если t= 3,5; б) t, если s = 30.

279. У мальчика было 80 р. Он купил х карандашей по 10 р. за штуку. Обозначив число рублей, оставшихся у мальчика, буквой у, задайте формулой зависимость у от х. Какова область определения этой функции?

280. Для сельской библиотеки ученики шестых и седьмых классов собрали 315 книг. Сколько книг собрали семиклассники, если известно, что они собрали на 10 ⁰/0 книг больше, чем шестиклассники?

281. Отметьте в координатной плоскости точки М (О; —4) и N(6; 2) и соедините их отрезком. Найдите координаты точки пересечения этого отрезка с осью х.

282. Отметьте в координатной плоскости точки А (—2; —3) и В (4; 5) и соедините их отрезком. Найдите координаты середины отрезка АВ.

14. График функции

Рассмотрим функцию, заданную формулой 6

где —2 З.

По этой формуле для любого значения аргумента можно найти соответствующее значение функции.

В таблице указаны некоторые значения аргумента и СООТВеТСТвующие им значения функции:

	х		-2	-1		1	2	з
			6	з	2	1,5	1,2	1
62		Глава ll
62

Рис. 11 Рис. 12

Каждую из найденных пар значений х и у изобразим точкой в координатной плоскости, считая значение х абсциссой, а соответствующее значение у ординатой (рис. 11). Выбирая другие значения х из промежутка от —2 до З и вычисляя соответствующие им 6

значения у по формуле у = , будем получать другие пары значе-

ний х и у. Каждой из этих пар также соответствует некоторая точка координатной плоскости. Все такие точки образуют график функ-

ции, заданной формулой у = , где —2 х З (рис. 12).

О п р е д е л е н и е, Графиком функции «называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Пример 1. Построим график функции, заданной формулой

у = х(б — х), где —1 х 5.

Составим таблицу соответственных значений аргумента и функции:

х	-1		1	2	з	4	5
У			5	8	9	8	5

5 5. и








		2





			-4
			-4

Отметим в координатной плоскости точки, координаты которых указаны в таблице. Соединим их плавной линией (рис. 13). Получим график функции, заданной формулой

где —1 х 5. <

Чем больше отметим точек, принадлежащих графику, и чем плотнее они будут расположены, тем точнее будет построен график функции.

С помощью графика функции по значению аргумента можно найти соответствующее значение функции. Можно также решить обратную задачу: по значению функции найти те знаРис. 13 чения аргумента, которым оно соответствует.

Пример 2. По графику функции, изображённому на рисунке 14, найдём: а) значение функции при х = З; б) значения х, при которых значение функции равно 7.

Рис. 14

а) Через точку оси х с абсциссой З проведём перпендикуляр к оси х. Точка пересечения этого перпендикуляра с графиком функции имеет координаты (З; 5). Значит, при х = З значение функции равно 5.

б) Проведём через точку оси у с ординатой 7 прямую, параллельную оси х, Эта прямая пересекает график в двух точках: с координатами (5; 7) и (9; 7). Значит, функция принимает значение, равное 7, при х = 5 и при х = 9,

График даёт наглядное представление о зависимости между величинами. Так, по графику температуры воздуха можно узнать, когда температура равнялась нулю, была выше нуля, ниже нуля, возрастала, убывала и т. д. Например, с помощью графика, изображённого на рисунке 8, можно определить, что температура была равна О ^ос в 9 ч и в 22 ч; была положительной с 9 до 22 ч; возрастала с З до 15 ч.

64	Глава П

На практике часто используются приборы для автоматической регистрации хода того или иного процесса (изменения в течение суток атмосферного давления, изменения в течение суток уровня моря, изменения давления пара в цилиндре двигателя в зависимости от положения поршня). Эти приборы вычерчивают графики соответствующих функциональных зависимостей. Так, с помощью кардиографа получают графическое описание работы сердца, сейсмограф позволяет получить графическое описание колебаний земной поверхности.

283. Функция задана формулой у = х (х — З), где —2 х 2. Заполните таблицу и постройте график этой функции.

	-2	-1,5	-1	-0,5	О	0,5	1	1,5	2
У

284. Принадлежат ли точки А (4; 2), В (1; —4) и С (1; 4) графику функции, заданной формулой у = 2х — 6? Укажите две точки, одна из которых принадлежит этому графику, а другая нет.

285. Кривая МЛ^Г— график некоторой функции (рис. 15). Найдите по графику значение функции, соответствующее значению ар-





					д

										х:

Рис. 15 Рис. 16

286. Используя график функции (рис. 16), заполните таблицу:

х	-3	-1,5	-0,5		0,5	3,2

Укажите пять значений аргумента, которым соответствуют положительные значения функции, и пять значений аргумента, которым соответствуют отрицательные значения функции.

ё 5. и

Макарычев. 7 кл.

287. (Для работы в парах.) Кривая, изображённая на рисунке 17 — график некоторой функции. Используя график, найдите:

а) значения у при х = —3; —2;

б) значения х, которым соответствуют у

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их. 2) Проверьте друг у друга правильность выполнения за-

дания. Рис. 17 З) Исправьте ошибки, если они допущены.

4) Обсудите возможность существования двух искомых значений в случае а) и в случае б).

288. Пользуясь графиком функции, изображённым на рисунке 17, укажите два каких-либо значения аргумента, при которых функция принимает:

а) положительные значения;

б) отрицательные значения.

289. Измеряя в течение десяти лет каждый год в день рождения рост ребёнка, построили график зависимости роста от возраста ребёнка (рис. 18). Пользуясь графиком, найдите:

а) каков был рост ребёнка в З года; в 6 лет; в 9 лет;

б) на сколько сантиметров вырос ребёнок за первые пять лет жизни; за последующие пять лет жизни.

l, ет

Рис. 18

66	Глава

6	у,мм








80

60

4


		х,л

Рис. 19

290. (Для работы в парах.) На рисунке 19 изображены графики зависимости высоты уровня жидкости от её объёма в двух сосудах различной формы, но одной и той же ёмкости З л. Пользуясь графиками, найдите:

а) какое количество жидкости надо налить в каждый сосуд, чтобы уровни жидкости в них были одинаковы;

б) сколько жидкости надо налить во второй сосуд, чтобы получить высоту уровня такую же, как в первом сосуде, когда в него налито 1,5 л жидкости.

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их,

2) Объясните друг другу, как вы рассуждали при выполнении задания, и изобразите схематически, какую примерную форму имеют эти сосуды.

291. Время, за которое маятник совершает полное колебание, т. е. из положения ОА переходит в положение ОС, а затем снова возвращается в положение ОА (рис. 20), называется периодом колебания маятника. Изучая зависимость периода колебания маятника Т от длины ни-

ти l, составили таблицу:

l, см	зо	50	60	80	100
			1,6		2,0

Постройте график зависимости периода колебания маятника Т от длины нити l.

5 5. и

292. Измеряя через каждую минуту температуру воды в баке, составили таблицу:

х, миц	о	1	2	з	4	5	6	7	8	9	10	11	12
у, ос	14	28	41	54	66	76	85	93	98	100	100	100	100

Постройте график зависимости у от х (масштаб: 1 см на оси х соответствует 1 мин, 1 см на оси у соответствует 10 ^ос). Используя график, ответьте на вопросы:

а) какую температуру имела вода через 4 мин, через 5,5 мин, через 9 мин, через 10,7 мин после начала нагревания;

б) через сколько минут после начала нагревания температура воды стала равной 41 ^ос; 60 ^ос; 95 ^ос?

293. (Для работы в парах.) На рисунке 21 изображены графики зависимости тормозного пути автомобиля от скорости его движения на сухом асфальте (кривая ОА), на мокром асфальте (кривая ОВ), при гололёде (кривая ОС). Для каждого случая ответьте на вопросы:

а) чему равен тормозной путь автомобиля при скорости 50 км/ч;

б) с какой скоростью должен двигаться автомобиль, чтобы его тормозной путь не превышал 60 м? 1) Выполните каждый задания а) и б).

2) Сравните полученные ответы. Исправьте ошибки, если они допущены.

З) Обсудите, насколько велико различие в тормозном пути на сухом и мокром асфальте.

Рис. 21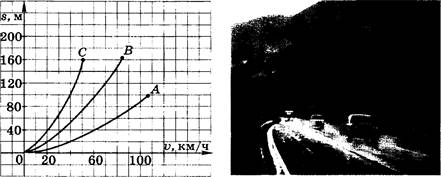

+ 3,13; в) -27х = 5 - 54х;

0,4х - 2,5.

68	Глава ll

295. В автопарке было в 1,5 раза больше грузовых машин, чем легковых. После того как автопарк получил ещё 45 легковых автомашин, а 12 грузовых машин передал фермерам, в нём стало легковых машин на 17 больше, чем грузовых. Сколько всего автомашин было в автопарке?

296. Верно ли, что:

в) 7+ 2424 : (11,8 + 0,2) + < 200;

г) (3,08 - 2,16) : 8- 0,17 0?

Контрольные вопросы и задания

Приведите пример функциональной ной от другой. Укажите независимую Объясните на примере функции,

а) как по значению аргумента функции; б) как найти значения указанное значение функции.

Что называется графиком функции? Покажите, как с помощью графика чение функции, соответствующее б) значения аргумента, которым функции. Используйте для этого на рисунке 15.

зависимости одной перемени зависимую переменные. заданной формулой у = 6х + 12: найти соответствующее значение аргумента, которым соответствует

функции можно найти: а) зназаданному значению аргумента; соответствует данное значение график функции, изображённый

ЛИНЕЙНАЯ ФУНКЦИЯ

15. Прямая пропорциональность и её график

Рассмотрим пример. Пусть — объём железного бруска в кубических сантиметрах, т — его масса в граммах. Так как плотность железа равна 7,8 г/см^з, то т = 7,8 у. Зависимость массы железного бруска от его объёма является примером функции, которая задаётся формулой вида у = Кх, где х — независимая переменная, К — число, отличное от нуля.

Такую функцию называют прямой пропорциональностью.

О п р е д е л е н и е, Прямой пропорциональностью называется функция, которую можно задать формулой вида у = Ь, где х — независимая переменная, — не равное нулю число.

Число К в формуле у = Кх называется коэффициентом прямой пропорциональности.

Из формулы у = Кх, где * О, находим, что если х1 и х2 — значения аргумента, причём * О, х2 * О, а и — соответствующие им значения функции, то = кх2. Отсюда

т. е. верна пропорция

С этим и связано название «прямая пропорциональность» в отличие от «обратной пропорциональности», с которой вы познакомитесь позже.

В повседневной жизни мы часто встречаемся с зависимостями между переменными, которые являются прямыми пропорциональностями.

Приведём примеры.

Пример 1. Путь s км, пройденный автомобилем за t ч с постоянной скоростью 70 км/ч, вычисляется по формуле s = 70t, где t > О, т. е. зависимость s от t является прямой пропорциональностью.

Пример 2. Стоимость р товара в рублях по цене 15 р. за килограмм вычисляется по формуле

Р = 15х, где х — масса товара в килограммах. Зависимость р от х является прямой пропорциональностью.

П ри мер З. Длина окружности С вычисляется по формуле С = 2nr,

где r — радиус окружности, п — число, приближённо равное З, 14. Значит, зависимость С от r является прямой пропорциональностью (коэффициент пропорциональности здесь равен 2“).

Выясним, что представляет собой график прямой пропорциональности.

В качестве примера рассмотрим функцию у = 0,5х и построим график этой функции.

70	Глава ll

Рис. 22 Рис. 23

Область определения функции у = 0,5х — множество всех чисел. Составим таблицу соответственных значений переменных х и у для некоторых значений аргумента х:

	0,5		1,5		2,5			3,5
	0,25	0,5	0,75		1,25			1,75

-0,5		-1,5		-2,5			-3,5
-0,25		-0,75		-1,25		-1,5	-1,75

Отметим в координатной плоскости точки, координаты которых помещены в таблице (рис. 22). Можно заметить, что все отмеченные точки принадлежат некоторой прямой, проходящей через начало координат. Проведём эту прямую. Получим график функции у = 0,5х (рис. 23).

Рассуждая аналогично, можно построить, например, график функции у = —1,5х (рис. 24). Этот график, так же как и график функции у = 0,5х, является прямой и проходит через начало координат.

Вообще,

график прямой пропорциональности представляет собой прямую, проходящую через начало координат.

Чтобы построить график функции у = Кх, достаточно найти координаты какой-нибудь точки графика этой функции, отличной от начала Рис. 24

			8
	-3-


-4			4



		-8		х




			—6

	-4.

рис. 25 рис. 26

координат, отметить эту точку и через неё и начало координат провести прямую.

Построим, например, график функции у = 1,5х. Пусть х = 2, тогда у = З, Построим точку А (2; З) и через неё и начало координат проведём прямую. Эта прямая является графиком функции у = 1,5х (рис. 25).

Расположение графика функции у = Кх в координатной плоскости зависит от коэффициента К. Из формулы у = Кх находим, что если х = 1, то у = К. Значит, график функции у = Кх проходит через точку (1; К). При К > О эта точка расположена в первой координатной четверти, а при К < О — в четвёртой. Отсюда следует, что при К > О график прямой пропорциональности расположен в первой и третьей координатных четвертях, а при К < О — во второй и четвёртой.

На рисунке 26 построены графики прямой пропорциональности при различных значениях К.

297. Велосипедист движется равномерно со скоростью 12 км/ч. Напишите формулу, выражающую зависимость пройденного пути s (в километрах) от времени движения t (в часах). Является ли эта зависимость прямой пропорциональностью?

298. Является ли прямой пропорциональностью функция, заданная формулой:

а) у = —5х; б) у = 5х ²;

299. Прямая пропорциональность задана формулой у

Найдите значение у, соответствующее х, равному

72	Глава ll

ЗОО. Постройте график прямой пропорциональности, заданной формулой:

а) у = 3х; д) у = 2,5х;

б) у = —1 5х е) у = —4,5х.

301. (Для работы в парах.) Задайте формулой прямую пропорциональность, график которой симметричен графику функции у = 9х:

а) относительно оси х; б) относительно оси у.

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

2) Проверьте друг у друга правильность выполнения задания.

302. Постройте график функции, заданной формулой у = —0,5х. С помощью графика найдите:

а) значение у, соответствующее х, равному —2; 4; 1;

б) при каком х значение у равно —1; О; 2,5.

Существует ли такое х, при котором у = —150? Если существует, то вычислите его.

303. Принадлежат ли графику функции у = —0,5х точки А (О; 1), щ-1; 0,5), се; -1), D(4•,

304. Известно, что график прямой пропорциональности проходит через точку А (З; 21). Проходит ли этот график через точку В (—7; —49); точку С (—5; 3,5); точку D(O,8; —5,6)?

305. (Для работы в парах.) Покажите схематически, как расположен график функции, заданной формулой:

а) у = 1,7х; в) у = 0,9х; д) у = Кх, где К > О; = -3,1х•, г) у = -2,3х; е) у = Кх, где К < О.

1) Распределите, кто выполняет задания а), б), а кто — задания в), г), и выполните их.

2) Проверьте друг у друга правильность выполнения заданий. З) Обсудите, какой вид имеет график функции у = Кх в заданиях д) и е).

306. Для каждого графика прямой пропорциональности, изображённого на рисунке 26, напишите соответствующую формулу.

307. Турист вышел из города и через х ч находился на расстоянии у км от него. Зависимость у от х показана в таблице:

х	о	0,5	1	2	2,5	З	3,5	4
	о	2,1	4,0	7,9	10,1	12,1	14	16,1

В координатной плоскости отметьте эти точки и покажите с помощью линейки, что они расположены почти на прямой. Составьте формулу, которая приближённо выражает зависимость у от х.

308. На рисунке 27 построены графики движения пешехода (отрезок ОВ) и велосипедиста (отрезок ОА). С помощью графиксов ответьте на вопросы:

а) какое время был в пути пешеход и какое время — велосипедист;

б) какой путь проделал пешеход и какой путь проехал велосипедист; в) с какой скоростью двигался 27 Рис. пешеход и с какой — велосипедист;

г) во сколько раз путь, который проехал за 2 ч велосипедист, больше пути, пройденного за то же время пешеходом?

309. На рисунке 28 изображён график зависимости удлинения у стальной проволоки от силы Е, под действием которой проволока растягивается. Укажите границы изменения силы Е, при которых зависимость удлинения проволоки от силы F является прямой пропорциональностью.

Рис. 28

310. Решите уравнение:

а) 1 1,7х + 2) = 3 4 6) 5 - о,2у = о,зу - 39.

311. Упростите выражение:

а) -21 (4 - 100) - 54а; 6) 28 - 10d + + 18).

312. Известно, что а > О. Сравните с нулём значение выражения: а 4

а) 5а; б) —10а; д) е)

74	Глава ll

1 6. Линейная функция и её график

Рассмотрим примеры функций.

П ри мер 1. На шоссе расположены пункты А и В, удалённые друг от друга на 20 км (рис. 29). Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч. За t ч мотоциклист проедет 50t км и будет находиться от А на расстоянии 50t + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой = 50t + 20, где t О.

Рис. 29

Пример 2. Ученик купил тетради по З р. за штуку и ручку за 5 р. Обозначим число купленных тетрадей буквой х, а стоимость покупки (в рублях) буквой у. Получим у = 3х + 5,

где х — натуральное число.

В обоих примерах мы встретились с функциями, заданными формулами вида у = Кх + Ь,

где х — независимая переменная, К и Ь — числа.

Такие функции называют линейными функциями.

О п р е д е л е н и е. Линейной функцией называехса функция, которую можно задать формулой вида у = кх + Ь, где х — независимая переменная, и Ь — некоторые числа.

Прямая пропорциональность является частным случаем линейной функции. Действительно, при Ь = О формула у = Кх + Ь принимает вид у = Кх, а этой формулой при К * О задаётся прямая пропорциональность.

Выясним, какой вид имеет график линейной функции.

Рассмотрим, например, функцию у = 0,5х + 2. Сравним значения функций у = 0,5х + 2 и у = 0,5х при одних и тех же значениях х.

	—4	-2	о	2	4	6
0,5х	-2	-1	о	1	2	з
0,5х + 2		1	2	з	4	5

Из приведённой таблицы и формул у = 0,5х и у = 0,5х + 2 ясно, что для любого значения аргумента х значение функции у = 0,5х + 2 на 2 единицы больше значения функции у = 0,5х. Если график функции у = 0,5х сдвинуть на 2 единицы вверх (т. е. в направлении оси у), то каждая точка (хо; уо) графика функции у = 0,5х перейдёт в точку (хо; уо + 2) графика функции у = 0,5х + 2. При этом любая точка графика функции у = 0,5х + 2 получается из соответствующей точки графика функции у = 0,5х.

Следовательно, график функции у = 0,5х + 2 есть прямая, параллельная графику функции у = 0,5х, проходящая через точку (0; 2) (рис. 30).

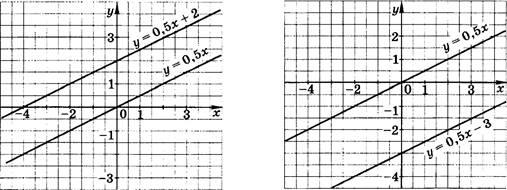
Рис. ЗО Рис. 31

Аналогично можно показать, что графиком функции у = 0,5х — З является прямая, параллельная прямой у = 0,5х и проходящая через точку (О; —3) (рис. 31). Вообще

Формула у = Кх + Ь при К = О принимает вид у = Ь. В этом случае графиком функции у = Кх + Ь является прямая, параллельная оси х при Ь О или сама ось х при Ь О.

76	Глава ll

-1

На рисунке 32 построен график функции у = З.

Таким образом,

Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки на координатной плоскости и провести через них прямую. Рис. 32

Пример З. Построим график функции у —

Функция у = 2х + З линейная, поэтому её графиком является прямая. Используя формулу у = 2х + З, найдём координаты двух точек графика:

если х = —2, то у = 2 • (—2) + З = —1; если х = 1, то у = 2 • 1 + 3 = 5.

Отметим точки А (—2; —1) и Щ 1; 5). Проведём через эти точки прямую (рис. 33). Прямая АВ есть график функции у = 2х + З.

При построении графика линейной функции часто бывает удобно в качестве одной из точек брать точку с абсциссой О.

Рис. 33 Рис. 34

Пример 4. Построим график функции у = —0,8х + 1.

Найдём координаты двух точек графика: если х = О, то у если х = 5, то у = -0,8 . 5 + 1 = -3.

Отметим точки М (О; 1) и К (5; —3) и проведём через них прямую (рис. 34). Прямая МК — график функции у = -0,8х + 1.

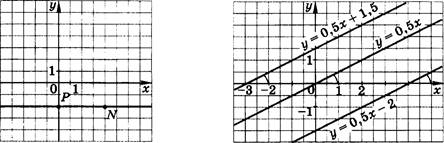
Рис. 35 Рис. 36

П ри мер 5. Построим график функции у 2.

Любому значению х соответствует одно и то же значение у, равное —2. Отметим две какие-нибудь точки с ординатой —2, например Р (О; —2) и N(4; —2), и проведём через них прямую (рис. 35). Прямая PN — график линейной функции у = —2. <

Расположение графика функции у = Кх + Ь на координатной плоскости зависит от значений коэффициентов К и Ь.

На рисунке 36 изображены прямые, которые являются графиками линейных функций, заданных формулами вида у = Кх + Ь с одинаковыми коэффициентами при х и различными значениями Ь. Все эти прямые параллельны и наклонены к оси х под одним и тем же углом. Этот угол зависит от коэффициента К.

Число К называют угловым коэффициентом прямой — графика функции у = Кх + Ь. Если К > О, то угол наклона прямой у = Кх + Ь к оси х острый; если К О, то этот угол тупой. На рисунке 37 для каждого случая этот угол показан с помощью стрелки.

Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые параллельны.

Рис. 37 Рис. 38

78	Глава ll

Из формулы у = Кх + Ь следует, что при х = О значение у равно Ь. Значит, график функции у = Кх + Ь пересекает ось у в точке с координатами (О; Ь). На рисунке 38 изображены прямые, которые являются графиками функций, заданных формулами вида у = Кх + Ь с различными К и одним и тем же значением Ь. Все эти прямые пересекаются в одной точке, лежащей на оси у.

Заметим, что если область определения линейной функции состоит не из всех чисел, то её график представляет собой соответствующую часть прямой. Например, это может быть полупрямая или отрезок.

313. Каждую секунду в бассейн поступает 0,5 м^зводы. Сколько кубометров воды станет в бассейне через х с, если сейчас в нём 120 м ^зводы? Задайте формулой зависимость объёма воды в бассейне от времени его наполнения. Является ли эта зависимость линейной функцией?

314. Длина прямоугольника х см, а ширина на З см меньше. Задайте формулами зависимость периметра прямоугольника от его длины и зависимость площади прямоугольника от длины. Какая из этих зависимостей является линейной функцией?

315. Ученик имел 85 р. На эти деньги он купил х марок по 10 р. После покупки у него осталось у р. Задайте формулой зависимость у от х. Является ли эта зависимость линейной функцией?

316. Является ли линейной функция, заданная формулой:

а) у = 2х — З;

2 5

317. Линейная функция задана формулой у = 0,5х + 6. Найдите значение у, соответствующее х = —12; О; 34. При каком х значение у равно —16; О; 8?

$18. Линейная функция задана формулой у = —3х + 1,5. Найдите:

а) значение у, если х = —1,5; 2,5; 4;

б) значение х, при котором у = -4,5, • о; 1,5.

319. Постройте график функции, заданной формулой:

г) у= х + 1,5;

в) у = —х + 4,5;

5 6.

320. (ЗаДача-исслеДование.) Дана линейная функция у = Кх + 4. При каком значении К график этой функции:

а) параллелен графику прямой пропорциональности у = —х;

б) не пересекает ось абсцисс;

в) пересекает ось абсцисс в точке с абсциссой З;

г) проходит через точку пересечения графиков функций

Обсудите ответы на поставленные вопросы,

321. Постройте график функции у = —10х + 40, выбрав масштаб: по оси х — в 1 см одна единица, по оси у — в 1 см 10 единиц. Найдите по графику:

а) значение у, соответствующее х = —2,5; 0,8; 3,5;

б) значение х, которому соответствует у = 70; —10; —30.

322. Не выполняя построения, найдите координаты точек пересечения с осями координат графика функции:

а) „-2,4х + 9,6; в) у = 1,2х + 6; 6) у - -0,7х - 28;

323. В какой точке пересекает ось х график функции, заданной формулой:

1 а) у = 0,4х — 12; з

324. Не выполняя построения графика функции у = 1,2х - 7 , выясните, проходит ли этот график через точку:

а) A(100; 113); в) щ-10•, 5);

6) щ-15; -25); г) D(300; 353).

325. В одной и той же координатной плоскости постройте графики функций у = 6, у = 3,2, у = —1, у = —5, у = О.

326. Постройте графики функций у = —2, у

327. Найдите координаты точки пересечения графиков функции:

а) у = 10х — 8 и у

б) у = 14 — 2,5х и у = 1,5х — 18;

в) у = 14х и у = х + 26;

г) у = —5х + 16 и у = —6.

328. На рисунке 39 изображён график одной из линейных функций. Укажите эту функцию.

Рис. 39

80	Глава ll

329. Один из графиков на рисунке 40 является графиком функции у = — х— 1. Укажите его.

Рис. 40

330. (Для работы в парах.) На рисунке 41 изображён график зависимости массы бидона с жидкостью от объёма жидкости, Найдите по графику:

а) массу пустого бидона;

б) массу бидона с одним литром жидкости;

в) массу одного литра жидкости;

г) объём жидкости в бидоне, если общая масса бидона с жидкостью равна З кг.

1) Выполните каждый задания а) и б).

2) Сравните полученные ответы. Исправьте ошибки, если они допущены.

З) Обсудите, как с помощью графика можно выполнить задания в) и г).

Рис. 41

5 6.

t мин,

		s, км











2
2
1
1

Рис. 42 Рис. 43

331. Из бака ёмкостью 12 л, наполненного доверху водой, равномерно вытекает вода. График зависимости V от t, где V — объём воды в баке (в литрах), а t — время вытекания воды (в минутах), построен на рисунке 42. Пользуясь графиком, найдите:

а) объём воды в баке через З мин;

б) время, через которое в баке осталось 4 л воды;

в) за какое время вытекла вся вода.

332. Дачник отправился из дома на автомобиле в посёлок. Сначала он ехал по шоссе, а затем по просёлочной дороге, сбавив при этом скорость. График движения дачника изображён на рисунке 43. Пользуясь графиком, ответьте на вопросы:

а) сколько времени ехал дачник по шоссе и сколько километров по шоссе он проехал; какая скорость автомобиля была на этом участке пути;

б) сколько времени ехал дачник по просёлочной дороге и сколько километров он проехал по этой дороге; какова была скорость автомобиля на этом участке пути;

в) за какое время дачник проехал весь путь от дома до посёлка?

333. В бак налили воду, температура которой 10 ^ос, и нагревали её до 100 ^ос, причём через каждую минуту температура повышалась на 1,5 ^ос. Задайте формулой зависимость температуры воды Т (в градусах Цельсия) от времени нагревания t (в минутах). Постройте график этой зависимости. Узнайте по графику:

а) какую температуру имела вода через 5 мин; через 10 мин после начала нагревания;

б) через какое время вода нагрелась до 85 ^ос.

82	Глава ll

334. Группа туристов отправилась со станции на турбазу. Первые 2 ч они шли со скоростью 4,5 км/ч. Затем сделали привал на 1 ч. На оставшуюся часть пути они затратили полтора часа, проходя её со скоростью 6 км/ч. Постройте график движения туристов.

8, км

—20

—12

335. (Для работы в парах.) На рисунке 44 изображены графики движения двух машин, следующих из города А в город В, расстояние между которыми 200 км. С помощью этих графиков ответьте на вопросы: а) какое время была в пути первая машина; вторая машина;

б) какая машина начала своё движение раньше;

в) с какой скоростью двигалась каждая машина;

г) какая машина прибыла в город Рис. 44 В раньше?

1) Распределите, кто отвечает на вопросы а), в), а кто — на вопросы б), г), и ответьте на них.

2) Проверьте друг у друга правильность ответов на поставленные вопросы.

З) Обсудите, что означает точка пересечения графиков,

336. Решите уравнение:

а) 30,9х - 1) - (х + 0,6) = -0,2; 6) 7 - (3,1 - оду) = -0,2у.

337. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей меньше, чем вторая, а третья — 30 ⁰/0 того числа деталей, которые изготовили первая и вторая бригады вместе. Сколько деталей изготовила каждая бригада?

338. Запишите в виде выражения сумму трёх последовательных натуральных чисел, меньшее из которых равно: а) п; б) п — 1;

в) п + 4. Упростите записанное выражение.

Контрольные вопросы и задания

пропорциональности.

Сформулируйте определение прямой Что является графиком прямой ить график прямой пропорциональности?

Как расположен в координатной при и при К < 0?

пропорциональности? Как постро-

плоскости график функции у = кх

ё 6.

Дайте определение линейной функции.

Что является графиком линейной функции? Как построить график линейной функции?

В каком случае графики двух линейных функций пересекаются и в каком случае они являются параллельными прямыми? В каких координатных четвертях расположен график функции: у = бх; у = 0,5х + 4; у = 3х — 1; у = —3?

Для тех, кто хочет знать больше

17. Задание функции несколькими формулами

Ранее вы встречались с примерами, когда функция задавалась одной формулой. Однако нередко встречаются ситуации, когда функцию задают несколькими формулами. Приведём примеры.

Пр имер 1. Турист первую часть пути от дома до станции шёл полтора часа со скоростью 6 км/ч. Затем полчаса он отдыхал, а после отдыха оставшуюся часть пути до станции он прошёл за один час со скоростью 5 км/ч.

Расстояние s (в километрах) от дома до места нахождения туриста является функцией времени t (в часах). Покажем, что эту функцию можно задать тремя формулами.

Когда время t изменяется от 0 до 1,5 ч, расстояние от туриста до дома равно 6t км, т. е.

s = 6t, если 0 1,5.

В период от 1,5 до 2 ч расстояние от туриста до дома остаётся неизменным, равным 9 км, т. е.

S = 9, если 1,5 2.

Когда время t изменяется от 2 до З ч, расстояние от туриста до дома равно 9 + 5(t — 2) км, т. е.

s = 5t — 1, если З.

Это можно записать короче:

6t, если t< 1,5,

9, если 2,

5t — 1, если З.

На рисунке 45 изображён график этой функции.

	Глава

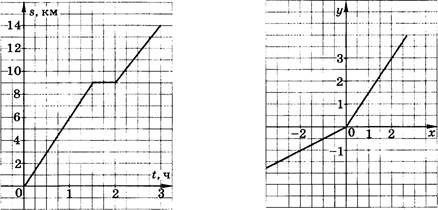
Рис. 45 Рис. 46

Пример 2. Построим график функции у = х + 0,51х1.

Освободимся от знака модуля. Если х < О, то lxl = —х. Значит, у = х — 0,5х = 0,5х при х < О.

Если х > О, то = х. Значит, у = х + 0,5х = 1,5х при х О. Итак, данную функцию можно задать двумя формулами:

0,5х, если х < О,

1,5х, если х Э О.

На рисунке 46 изображён график этой функции. Он состоит из двух лучей.

Пример З. На рисунке 47 изображён равнобедренный треугольник АВС, в котором ZC = 90 ⁰, гипотенуза АВ = 4 см. Отрезок MN, перпендикулярный А В, движется так, что точка М перемещается от точки А до точки В. При этом длина отрезка АМ, равная х см, изменяется от О до 4 см. Покажем, что площадь у (в квадратных сантиметрах) отсекаемой отрез- с ком MN фигуры (треугольника AMN или четырёхугольника AM'N'C) является функцией длины отрезка, зададим эту функцию формулами и построим её график. При этом воспользуемв ся формулой площади треугольника м D м

S = —ah, где а — основание треуголь- рис. 47

ника, h — его высота.

Если переменная х изменяется от О до 2 (точка М перемещается от точки А до точки О), то отсекаемая фигура представляет

Для тех, кто хочет знать больше

собой треугольник AMN, площадь которого равна — АМ • МА^Т,

= —х². Если же переменная х изменяется от 2 до 4 (точ2 ка М ' перемещается от точки D до точки В), то отсекаемая фигура представляет собой четырёхугольник AM'N'C, площадь которого равна разности площади треугольника АВС и площади тре-

1 угольника M'N'B, т. е. у = 4 — —(4 — х)².

Легко понять, что каждому значению х, где О < х < 4, соответствует единственное значение у, т. е. зависимость у от х является функцией. Эту функцию можно задать двумя формулами:

—х ², если О < х 2, 2

4 — (4 — ху, если 2 < х 4.

Для построения графика составим таблицу:

з!

Построив в координатной плоскости точки, координаты которых записаны в таблице, и соединив эти точки плавной линией, полу-


4
4


з
з






1
1

чим график рассматриваемой функции (рис. 48).

З а м е ч а н и е. Задавая функцию у = f(x) несколькими формулами, необходимо следить за тем, чтобы каждому значению х соответствовало единственное значение у. В противном случае такая зависимость не будет являться функцией. Например, зависимость х, если х З,

2х, если х З

не является функцией, так как в этом случае число З — общее значение переменной как для формулы у = х, так и для формулы у = 2х. Поэтому значению х = З соответствует не одно,

Рис. 48 а два значения у: ут З и .џ2 = 6.

86	Глава lI

Функция задана графиком (рис. 49). Задайте эту функцию аналитически, т. е. одной или несколькими формулами.

Из бака ёмкостью 20 л, заполненного водой (рис. 50), через открытый кран равномерно вытекает вода со скоростью 2 л в минуту. Через кран может вытечь 0,9 всего объёма воды в баке, так

как кран расположен выше дна
бака. Объём воды V (в литрах) в баке зависит от времени х (в минутах), когда кран открыт. За-	Рис. 49

дайте зависимость от х аналитически, если известно, что кран был открыт в течение 12 мин.

Постройте график функции: —х, если х < —1, х, если х > —1; 2х, если —1 х < 1,

З— х, если 1 х 4.

Постройте график функции:

а) у = 0,251xl + 1;

Рис. 50

Функция задана двумя формулами:

--х + 2, если х < О, х + 2, если х О.

Задайте эту функцию одной формулой, используя знак модуля. На рисунке 51 изображён график функции, область определения которой есть множество значений х, таких, что —2 х 6.

Задайте эту функцию аналити-
чески.	Рис. 51

для тех, кто хочет знать больше

Изменение температуры Т (в градусах Цельсия) воды в баке описано с помощью формул:

4t + 20, если О < t < 20,

100, если 20 t 30,

1 —— t+ 110, если 30 90. з

Найдите значение Т при t = 10; 20; 30; 45; 60; 90. Какой физический смысл имеет рассматриваемый процесс, когда О t < 20? когда 20 t 30? когда 30 < t 90?

Пешеход, отправившийся из дома на прогулку, оказался через t ч на расстоянии s км от дома. Зависимость s от t задана тремя формулами:

6t, если — 6'

5, если — t 1,

—5t + 10, если 1 <

Найдите расстояние s при t, равном

• 1; 1,5; 2.

На рисунке 52 изображён график движения автомобиля из пункта А в пункт В. Задайте эту функцию аналитически. С какой скоростью двигался автомобиль до остановки? С какой скоростью двигался автомобиль после остановки? Рис. 52

упражнения к главе ll

К параграфу 5

348. Масса одного кубического сантиметра ртути равна 13,6 г. Масса см^зртути равна т г. Задайте формулой зависимость:

а) т от У; б) от т.

349. При делении числа у на число х в частном получается 5, а в остатке 10. Задайте формулой функцию у от х. Какова область определения этой функции? Найдите две пары соответственных значений х и у.

350. Турист вышел с турбазы А в направлении железнодорожной станции В. На рисунке 53 дан график зависимости пути, прой-

88	Глава

Рис. 53 Рис. 54

денного туристом, от времени движения. Выясните: а) какое время затратил турист на путь из А в В; б) с какой средней скоростью двигался турист; в) сколько минут он затратил на первый привал и сколько затратил на второй привал; г) сколько километров турист прошёл за первый час движения и сколько за последний; д) какое время было затрачено туристом на первые 8 км и какое на последующие 8 км.

351. Какова область определения функции, заданной формулой:

7 8

352. Бригада по плану должна изготовить 150 деталей за смену. Однако она перевыполнила план на х % , Составьте формулу, выражающую зависимость у от х, где у — число изготовленных бригадой деталей. Найдите по формуле:

а) значение у, если х = 10;

б) значение х, при котором у = 180.









										х

353. Из квадрата со стороной 10 см вырезали прямоугольник со сторонами 8 см и х см (рис. 54). Обозначив площадь оставшейся части квадрата (в квадратных сантиметрах) буквой у, выразите зависимость у от х формулой. Найдите:

а) значение у, если х = 2,5; 4;

б) значение х, если у = 20; 36.

На рисунке 55 чёрной линией изображён график первой функции, а цветной — график второй функции. При каких значениях аргумента значение первой функции:

а) равно значению второй;

б) больше значения второй;

в) меньше значения второй? Рис. 55

дополнительные упражнения к главе П

355. Рыболов пошёл из дома на озеро, где ловил рыбу. Затем он возвратился обратно. График движения рыболова показан на рисунке 56. Узнайте по графику: а) каково расстояние от дома до озера; б) сколько часов шёл рыболов до озера и сколько часов он затратил на обратный путь; в) сколько часов был рыболов на озере; г) на каком расстоянии от дома был рыболов через 1 ч после выхода из дома;

д) через сколько часов после выхода рыболов был на расстоянии 6 км Рис. 56 от дома; е) какова средняя скорость рыболова на пути к озеру и какова на обратном пути.

Изучая зависимость объёма жидкости в сосуде от высоты h её уровня, получили таблицу:

	з	6	9	12	15	18
	1,2	3,1	5,6	9,7	14,7	21

Постройте график функции V от Ь. Узнайте по графику: а) сколько литров жидкости налили в сосуд, если высота уровня стала равной 5 см; 10 см;

б) какой будет высота уровня жидкости в сосуде, если в него налить 4 л; 10 л.

К параграфу 6

357. Постройте график функции, выбрав соответствующий масштаб: а) у = 100х; 6) 0,02х.

358. Какое расстояние у (в километрах) проедет велосипедист за х ч, если будет двигаться равномерно со скоростью 15 км/ч? Постройте график зависимости у от х (масштаб по оси х: в 1 см — 15 км; по оси у: в 1 см — 1 ч). С помощью графика ответьте на вопросы:

а) какой путь проедет велосипедист за З ч; за З ч 40 мин;

б) сколько времени затратит велосипедист на путь в 50 км?

359. Является ли линейной функция, заданная формулой:

4х - 7

в) у = х(б — х);

б)

90	Глава ll

360. Функция задана формулой у = 0,2х — 4. Найдите значение функции, соответствующее значению аргумента, равному —25; —12; 45; 60. При каком значении аргумента значение функции равно О; 1? Существует ли такое значение х, при котором:

а) значение функции равно значению аргумента;

б) значение функции противоположно значению аргумента?

Зная, что зависимость у от х является линейной функцией, заполните таблицу:

			2	4	6	6)			-10	о	10	зо
		-8	12			6)	У	-15		5	6		15

а)

В таблице указаны некоторые значения аргумента и соответствующие им значения линейной функции. Подберите формулу, которой можно задать эту функцию.

х	1	2	з	4	5	6	7
	11	21	31	41	51	61	71

363. Масса одного гвоздя равна 5 г, а масса пустого ящика равна 400 г. Какова масса т (в граммах) ящика, в котором лежит х гвоздей? Составьте формулу, выражающую зависимость т от х. Является ли функция, заданная этой формулой, линейной?

При каком значении а точка А (а; —1,4) принадлежит графику прямой пропорциональности у = 3,5х?

365. Функция задана формулой у = — х + З, где —4 х 8. Построй4 те график этой функции и укажите все целые значения, которые может принимать эта функция.

366. Скорость распространения звука в воздухе в зависимости от температуры воздуха может быть найдена приближённо по формуле = 331 + 0,6t, где — скорость (в метрах в секунду), — температура (в градусах Цельсия). Найдите, с какой скоростью распространяется звук в зимний день с температурой —35 ^ос и в летний день с температурой +30 ^ос.

367. Пересекает ли ось х график линейной функции и если пересекает, то в какой точке:

а) у : 100 - 25х•,

в) у = 200х; д) у = -15;

г) у = —75х; е) у = 15?

дополнительные упражнения к главе ll

Покажите схематически в одной координатной плоскости, как расположены графики функций у = ах и у = bx, если:

б) а < О, Ь < О и al < lbl.

369. График некоторой линейной функции вида у = Кх + 1 параллелен графику функции у = —0,4х. Найдите значение коэффициента К и выясните, принадлежит ли этому графику точка МФО; -19).

370. Задайте формулой линейную функцию, графиком которой служит прямая, проходящая через точку А (2; З) и параллельная графику функции у = 1,5х — З. Постройте её график.

371. График линейной функции — прямая, параллельная оси абсцисс и проходящая через точку М (5; 8). Задайте эту функцию формулой.

372. Не выполняя построения, найдите координаты точки пересечения графиков линейных функций:

а) у = 4х + 9 и у = 6х — 5; в) у = 10х — 7 и у = 5;

б) у = 16х — 7 и у = 21х + 8; г) у = 0,1х и у = 14.

Графики линейных функций у = 3х + 2, у = —2х + З и у = 0,5х — 2 ограничивают треугольник. Лежит ли начало координат внутри этого треугольника?

92	Глава ll

ПОКАЗАТЕЛЕМ

вы уже знакомы с понятием степени с натуральным показателем. Теперь вы изучите свойства степеней с натуральными показателями, научитесь выполнять умножение и деление степеней, возведение степени в степень. В повседневной жизни вам пригодится умение выполнять возведение в степень с помощью калькулятора. В этой главе вы впервые встретитесь с понятием одночлена, правилами умножения одночленов и возведения одночлена в степень. Вы продолжите изучение функций — познакомитесь со свойствами и графиками функций у = х ²и у = х ^з, получите первые представления о графическом способе решения уравнений.

СТЕПЕНЬ И ЕЁ СВОЙСТВА

18. Определение степени

с натуральным показателем

Произведение нескольких одинаковых множителей можно записать в виде выражения, называемого степенью. Например:

Повторяющийся множитель называют основанием степени, а число повторяющихся множителей — показателем степени.

Так, в выражении 5 ⁷число 5 — основание степени, а число 7 — показатель степени.

О п р е д е л е н и е. Степенью числа а с натуральным показателем п, большим 1, называется выражение а^п, равное произведению п множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

5 7. и

Запись а ^пчитается так: «а в степени п», «п-я степень числа а».

По определению степени а ¹= а, а ²= аа, а ^з= ааа, а⁴= аааа.

Вообще а ^п= аа...а.

п раз

Нахождение значения степени называют возведением в степень.

Приведём примеры возведения в степень:

3 ⁴= 3 . з . з . 3 = 81; 0 ²= 0.

( • • = -216; 9 ¹= 9.

I При возведении в степень положительного числа получается положительное число; при возведении в степень нуля получается нуль

При возведении в степень отрицательного числа может получиться как положительное число, так и отрицательное. На-

пример:

(-2) ¹= -2;

(-2)2 = • (-2) = 4;

(-2)3 = (-2) • (-2) • (-2) = -8;

(-2) ⁴= (-2) • (-2) • (-2) • (-2) = 16.

I Степень отрицательного числа с чётным показателем — положительное число.

Степень отрицательного числа с нечётным показателем — отрицательное число.

Действительно, произведение чётного числа отрицательных множителей положительно, а произведение нечётного числа отрицательных множителей отрицательно.

При вычислении значений числовых выражений, не содержащих скобки, принят следующий порядок действий: сначала выполняют возведение в степень, затем умножение и деление, далее сложение и вычитание.

Вычислим значения нескольких выражений, содержащих степени.

94	Глава lll

Пример 1. Найдём значение выражения 4 • 10 ³

» 1) 10 ³= 10 • 10 • 10 = 1000; 2) 4 . 1000 = 4000. Значит, 4 • 10 ³= 4000.

Пример 2. Найдём значение выражения —2 ⁶+ (—3)⁴.

1) 2 ⁶= 64; 2) -2 ⁶-64 3) (-3)⁴= 81; 4) -64 +81 = 17.

Значит, —2 ⁶+ (—3) ⁴= 17

Рассмотрим теперь, как находят значение степени с помощью калькулятора.

При мер З. Найдём с помощью калькулятора значение степени 2,7 ⁵

Так как степень 2,7 ⁵есть произведение пяти множителей, каждый из которых равен 2,7, то вычисления можно провести по схеме

Однако калькулятор позволяет вычислять значение степени проще, не набирая повторно основание степени и знак умножения. В нашем примере достаточно ввести число 2,7, нажать клавишу и 4 раза нажать клавишу Е. Получим более удобную схему вычислений:

ВЕННЕ.

В результате вычислений найдём, что 2,7 ⁵= 143,48907.

374. Запишите произведение в виде степени:

12 раз

1 1 1 1

25 раз и) (ху) (ху) (ху) (ху) (ху).

д) ссссссс;

ё 7. и

375.	Назовите основание и показатель степени:	5
	а) 3,5 ⁴; 6) в) (-100)⁴; Г) (—а)б, Д)	1 2
	Используя определение степени, представьте произведения.	степень в виде
376.	Выполните в степень:

возведение

в) 5 ³;ж) и)

з)

377. Найдите значение степени:

а) 25 ²;ж)

з)

378. Вычислите с помощью калькулятора:

а) 4,15 ³; 6) в) 1,42 ⁶; г) 2,08³: 1,56; д) 1,67⁴• 8,3.

379. Найдите с помощью калькулятора значение выражения:

а) 8,49 ⁴; в) 2,73 ⁵• 27,4; г) (1,39 + 380. Заполните таблицу:

1	2	з	4	5	6	7	8	9	10

381. Представьте:

25 24

а) в виде квадрата число: 0,81; ; 144; ; 1—• 0,0004;

169 25'

117

б) в виде куба число: 64; —216; 0,008; -

6427 '

в) в виде степени десяти число: 10; 100; 1000; 1 000 000;

г) в виде степени пяти число: 125; 625; 15 625.

382. Представьте в виде квадрата или куба число:

а) 8;

6) 81;

в) 125; г) 64; д) 0,001;

8 '

25 •

383. Сравните:

а) 71 ²и О;

б) (—25) ³и О;

384. Выполните действия:

в) (—0,4) ³;

• 552; е) _62 . (—12).

96	Глава lll

385. Найдите значение выражения, используя таблицу квадратов, помещённую на форзаце учебника:

а) 34 ²- 175; в) 42 ²• 9; д) 75 ²+ 25 ²; 6) 605 + 78 ²; г) 18 ²: 27; е) 59 ²- 36 ²386. Вычислите:

в) (-10) ⁶; д) 4 53ж) —2 ⁴• 15;

г) —10 ⁶; е)з) 2700 •

387. Выполните действия:

г) 10 ²— 32. ж) 11 — 3 ⁴;

д) (10 —— 8)5;

и) 4 ³— 22

388. Вычислите: 2

а) -1 ³+ (-2) ³; г) 10 — 5 • 2 ⁴; ж) 3⁴— ²

5 4 6) -6 ²- (-1) ⁴; з) • 3 ³- • 2 ⁴;

в) -8 ³+ (-3) ³; е) 2 . 5 ³+ 5 . 2 ³; и) 8 . 0,5 ³+ 25 • 0,2 ²

389. Окно в старинном особняке имеет прямоугольника, завершающегося полукругом (рис. 57). Составьте формулу для вычисления его площади S (в квадратных сантиметрах), если известно, что основание прямоугольника равно а см, высота прямоугольника в полтора раза больше основания. Найдите площадь окна, если а = 80. (Указание. Площадь круга равна ПР, где r — радиус круга, п 3,14.)

390. Составьте формулу для вычисления площади кольца, изображённого на рисунке 58. Найдите площадь кольца, если R = 6,4 см, r = 3,6 см.

Рис. 57 Рис. 58

5 7.

4 — Макарычев, 7 кл.

391. Найдите значение выражения:

а) 0,01у ⁴при у = —2; 2; —3; З; —10; 10

б) 2с ²+ З при с = -11; 11; о; -15; 15

392. Чему равны значения выражений:

а) х ²; —х ²; (—х) ²при х = —9; 9; —6; 6

б) х³; —х^з; (—х) ³при х = —4; 4; —3;

393. Вычислите значение выражения х ⁵+ х⁴+ х ^з+ х²+ х при х 3 -1; О; 10.

394. (ЗаДача-исслеДование.) Найдите всевозможные значения а, где а — натуральное число, при которых число 90 является наименьшим общим кратным чисел 15 и а.

1) Разложите на простые множители каждое из чисел 90 и 15. 2) Обсудите, какие множители должны входить в разложение числа а.

З) Сделайте вывод о значениях числа а.

395. Представьте произведение в виде степени с основанием а:

а) а ^за; б) а ⁴а ²; в) а ^за ^б, 20 12

396. Объясните, почему при любых значениях переменной х значения выражений 4х ²и (х — являются неотрицательными числами.

397. (Для работы в парах.) Даны выражения:

_а4, З + (5 — а)2, —а — аз,

За + 4, 04 -4- а 2 + 8 , —а ^б— 40 ⁸— 1, —08 — 9.

Какие из этих выражений принимают:

а) только положительные значения;

б) только отрицательные значения?

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

2) Проверьте друг у друга, верно ли выполнено задание. З) Исправьте ошибки, если они допущены.

398. Запишите в виде выражения:

а) квадрат суммы чисел х и 1;

б) сумму квадратов чисел а и Ь;

в) разность квадратов чисел т и п;

г) квадрат разности чисел т и п;

д) удвоенное произведение квадратов чисел х и у;

е) удвоенное произведение куба а и квадрата Ь.

399. Прочитайте выражение:

а) (х + у) ²,д) (х — у) ³; ж) 2(а — Ь)2; 2. з з. з) З(а2 + b2).

98	глава lll

400. Не выполняя построения, найдите координаты точек пересечения графика функции у = 1,2х — 30 с осью х и осью у.

401. Найдите координаты точки пересечения графиков функций:

а) у = —4х + 1,3 и у = х — 2,7;

б) у =—х + 8,1 и у = —3х + 7,9.

402. Каково взаимное расположение графиков функций:

19. Умножение и деление степеней

Выражение а ²а ³представляет собой произведение двух степеней с одинаковыми основаниями. Это произведение можно записать в виде степени с тем же основанием:

а ²а ³— (аа) • (ааа) = ааааа = а ⁵.

Значит,

02 аз — а2+3

Мы видим, что произведение а ²а ³равно степени с тем же основанием и показателем, равным сумме показателей перемножаемых степеней. Аналогичным свойством обладает произведение любых степеней с одинаковыми основаниями.

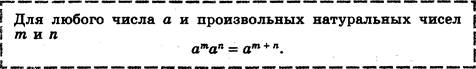
Для доказательства используем определение степени и свойства умножения. Представим выражение а ^Та ^Псначала в виде произведения множителей, каждый из которых равен а, а затем в виде степени а ^Та ^П= (аа...а) • (аа...а) = аа...а т раз п раз т + п раз

Таким образом,

отап + п

Доказанное равенство выражает основное свойство степени. Оно распространяется на произведение трёх и более степеней. На-

пример:

а ^Та ^Па ^к— а

Из основного свойства степени следует правило умножения степеней:

при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Приведём примеры:

5 У1у5 — У1 + 5 уб b2b4b3 = b2 + 4 + 3 b9

Выражение а ⁷: а ^зявляется частным двух степеней с одинаковыми основаниями. Оно имеет смысл при а * О. Если а * О, то это частное можно представить в виде степени с тем же основанием.

Действительно, так как а ^з• а ⁴= а ⁷, то по определению частного

а ⁷: а ^з= 0 ⁴, т. е. а ⁷: а ^з= а7-3

Мы видим, что частное а ⁷: а ^зпри а * О равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.

Аналогичным свойством обладает любое частное степеней с одинаковыми основаниями, отличными от нуля, в котором показатель степени делимого больше показателя степени делителя.

Равенство а ^т: а ^па ^{т п}будет доказано, если мы установим, что произведение а ^{т п}И а ^правно а ^т.

Применив к произведению а ^т- ^па ^посновное свойство степени, получим ат- пап = - п» п —

Значит, по определению частного а ^т: а ^п= а ^т- ^п

Из доказанного свойства следует правило деления степеней:

при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Приведём примеры:

= ^с8, р ⁷: Р = Р ⁷: р ¹= Р7

100	Глава lll

Мы вывели правило деления а ^тна а ^пдля случая, когда т > п.

Если это правило применить к частному а ^п: а ^д, то получится а ^п: а ^п= а ^П- ^П= а ^о.

Степень с нулевым показателем не была определена. Так как при всяком а О и любом натуральном п

то считают, что при а О

О п р е д е л е н и е. Степень числа а, не равного нулю, с нулевым показателем равна единице.

Например, 2 ⁰= 1 ( = 1. Выражение 0 ⁰не имеет смысла. Теперь после введения нулевой степени мы можем применять формулу а ^Та ^П— а ^т+ ^п(при а О) и в том случае, когда т = О или П = О. Формулу а ^т: а ^п= а ^Т- ^ппри а О можно применять при любых целых неотрицательных числах т и п, удовлетворяющих услоВИЮ т п.

403. Представьте произведение в виде степени:

а) х ⁵х ⁸, в) у ⁴у ⁹, д) х ⁹х; ж) 2 ⁶24. баз. г) b8b15. е) уу12,

Запишите в виде степени произведение:

а) т ^Зт ⁸, 7 с 12. д) аа ^з, ж) 5 ⁹• 58.

з 11.

405. Представьте выражение а ¹⁵в виде произведения двух степеней с одинаковыми основаниями, одна из которых равна:

а) а ^б, б) а ⁹; в) а ², г) а ^и.

406. Представьте степень в виде произведения двух степеней с тем же основанием каким-нибудь способом:

а) х ¹⁰, б) у15. в) 212. 517

407. Представьте выражение х ⁶в виде произведения двух степеней с основанием х всеми возможными способами.

408. Представьте в виде степени произведение:

а) х ²х ⁵х ⁴, в) тт ³т ²т ⁵, д) 10 ²• 10 ³• 10 ⁵;

б) у ^зу ²у; г) р4Р3РР', е) 3 ⁴• 3 ²• 3 ³• З.

1 01

409. Запишите в виде степени выражение:

а) т ³т ²т ⁸, в) хх ⁴х ⁴х; д) 78 . 7 . 74;

б) а ⁴а ³а ², г) п ⁵пп ³п ⁶, е) 5 • 5 ²• 5 ³• 5 ⁵

410. Представьте в виде степени:

а) 5 ⁸• 25; в) 6 ¹⁵• 36; д) 0,4 ⁵• 0,16;

6) 3 ¹²• 27; г) 2 ⁹• 32; е) 0,001 • 0,1 ⁴

411. Представив в виде степени выражение, найдите его значение по таблице степеней числа 2, помещённой на форзаце учебника:

а) 2 ⁴• 2; 6) 2 ⁶• 4; в) 8 . 2 ⁷; г) 16 • 32.

412. По таблице степеней числа З, помещённой на форзаце учебни-

ка, найдите значение выражения, представив его в виде степени с основанием З:

а) 3 ²• 3 ⁵; 6) 81 • 3 ⁶; в) 9 . 2187; г) 27 • 243.

41 з Представьте выражение в виде степени с основанием с: 4 2. б) (с2)4.

414. Представьте в виде степени частное:

а) х ⁵: х ^з, в) а ²¹: а; д) с ¹². с ^з•, эк) 3 ⁸: 3 ⁵•

б) у10 г) : Ь 18. е) р20 : Р10, 79 : 6,74

415. Выполните деление:

а) р10 : в) х ¹⁵ д) 10 ¹⁶: 10 ¹²'

4. 2,3 ¹⁶: 2,3+

е)

416. Найдите значение выражения:

а) 5 ⁶: 5 ⁴' в) 0,510

6) 10 ¹⁵: 10 ²; з

417. Найдите значение дроби:

86 О, 87

а) б) в)г) 84

418. Вычислите:

79 75 315 516 . 54 0,612

а) б) ' в) 518 г) 0,6⁴• 0,6⁵• 712 35 . 36

419. Упростите выражение:

а) х ^л• х^з, д) с ⁹•

1 02	Глава llI

420. Найдите значение выражения:

а) 3х⁰при х = 2,6;

2 б) —2,5у ⁰при у = —1 ; з

в) 10a2b0 при а = —3, Ь = —8;

2 1

г) 27а⁰с ³при а = —, с з

421. Выполните действия:

а) b ⁴b⁰; б) с ⁵: с^о, в) а ⁴а ⁰, г) х ³: х^о.

422. Представьте в виде квадрата или куба число:

в) 6,25; г) 0,064; д) —3 ²; е) 54.

8 9

423. Постройте график функции, заданной формулой у = х — З. Найдите по графику значения функции при х = 4 и х = 6.

Двигаясь со скоростью 70 км/ч, автомобиль за t ч прошёл расстояние s км. Задайте формулой зависимость s от t. Пользуясь этой формулой, найдите путь, который автомобиль прошёл за время от З ч 30 мин до 5 ч.

Пусть а — произвольное число. Сравните с нулём значение выражения:

а) ба ²; б) —а ²; в) а ²+ 4; г) (а + 4) ²; д) —а ²— 5.

426. Принадлежит ли графику функции, заданной формулой у = х ^з— 3х ², точка А (7; 196)? точка В (—5; —200)?

427. Кусок гранита объёмом 40 см ^зимеет массу 108 г. Какова масса куска гранита, объём которого на 35 см ^збольше?

20. Возведение в степень произведения и степени

Выражение (ab) ⁴является степенью произведения множителей а и Ь. Это выражение можно представить в виде произведения степеней а и Ь:

(ab) ⁴= ab • ab • ab • ab = (аааа) • (bbbb) = a ⁴b ⁴Значит,

(ab) ⁴= a ⁴b ⁴

Аналогичным свойством обладает любая натуральная степень произведения двух множителей.

103

По определению степени

(аЬ) ^П= (ab) • (ab) • • (аЬ).

п раз

Сгруппировав отдельно множители а и множители Ь, получим (ab) • (ab) • ... • (ab) = (аа...а) • (bb...b).

п раз п раз п раз

Воспользовавшись определением степени, находим (аа...а) • (bb...b) = а ^Пб ^П.

п раз п раз

Следовательно,

(аЬ) ^П= а ^ПЬ ^П. СЛ

Доказанное свойство степени произведения распространяется на степень произведения трёх и более множителей. Например:

(аЬс) ^П= а ^ПЬ ^Пс ^П; (abcd) ⁿ= а Ь с d . Отсюда получается правило:

чтобы возвести в степень произведение, достаточно возвести в эту степень каждый множитель и результаты перемножить.

Пример 1. Возведём произведение 2yz в пятую степень. Имеем (2yz) ⁵= 2 ⁵y ⁵z ⁵= 32y ⁵z ⁵.

Выражение (а ⁵) ³есть степень, основание которой само является степенью. Это выражение можно представить в виде степени с основанием а:

(а ⁵) ³— а ⁵а ⁵а ⁵— а ^{5 5}+ ⁵= 0 ^{5 з}

По определению степени а ^Та ^Т...а ^л

п раз

Согласно основному свойству степени п раз

п раз

104	Глава lll

Заменим сумму т + т + ... + т произведением тп.

п раз

Тогда получим п раз

а = а ^та

Следовательно,

(а ^т) ^п= а ^тп. 2

Из доказанного свойства степени следует правило:

при возведении степени в степень основание оставляют тем же, а показатели перемножают.

Пример 2. Представим выражение (а ⁴)³в виде степени с основанием а.

Имеем:

(а ⁴) ³— а

Свойства степеней, выраженные формулами (аЬ)^П= а ^пь ^пи (а ^т) ^п= а ^тп, имеют место и для степеней с нулевым показателем (если основания отличны от нуля).

428. Выполните возведение в степень:

а) (ху) ⁴, в) (2х) ³;	д) (—5х) ³;	ж) (—0,2ху) ⁴;
б) (abc) ⁵; г) (За) ²; 429. Возведите в степень:	е) (—10ab) ²;	з) (—0,5bd) ³.
а) (тп) ⁵, в) (—3у)4;	д) (10ху) ²;	ж) (—ат) ³,
б) (xyz) ², г) (—2ах) ³,	е) (—2abx)⁴;	з) (—хп) ⁴.

430. Найдите значение выражения:

а) (2 • 10) ³; в) (3 • 100) ⁴; • 20)2.

431. Докажите, что:

а) квадраты противоположных чисел равны;

б) кубы противоположных чисел противоположны.

432. Как изменится площадь квадрата, если его сторону увеличить в 2 раза? в З раза? в 10 раз? в п раз?

433. Как изменится объём куба, если его ребро увеличить в 2 раза? в З раза? в 10 раз? в п раз?

1 05

(Для работы в парах.) На покраску куба затратили 40 г краски. Хватит ли 1 кг краски, чтобы покрасить куб, ребро КОТОРОго в З раза больше?

1) Выскажите друг другу предположение об ожидаемом ответе.

2) Выполните самостоятельно вычисления.

З) Обсудите, подтвердились ли ваши предположения.

435. (Для работы в парах.) Бассейн, имеющий форму куба, наполняется водой через трубу за 40 мин. Успеют ли за 5 ч наполнить водой через ту же трубу бассейн, имеющий форму куба, ребро которого вдвое больше?

1) Выскажите друг другу предположение об ожидаемом ответе.

2) Выполните самостоятельно вычисления.

З) Обсудите, подтвердились ли ваши предположения.

436. Представьте в виде степени произведение:

а) 8х ³; 2 222. д) 32а ⁵;

б) а ⁷у ⁷; г) (—а) ³Н; е) 0,027т ^з.

437.	Найдите значение выражения:		10
	а) 2 ⁴• 5 ⁴, в) 0,2515 . 415. 7 2	д)	5 7
	6) 4 ³• 25 ³; г) • 1,57; з	е)	0,2 ⁶• 50 ⁷.
438.	Выполните возведение в степень:
	а) (х ³) ², в) (а ⁵) ⁴, д) (У2)5,		ж) (63)3;
	2)3. Г) (а ^б)³, 7)2.		з) (b5)2.

440. Запишите в виде степени с основанием х выражение: 6)4. 2х2. д) х ²х^Зх⁴,

2)2.

441. Представьте в виде степени с основанием а выражение:

а) (а5)2' б) а ⁵а ², в) (а ⁴) ³, г) а ^за ⁴,д) а ⁵а ⁵, е) (а ⁵) ⁵•

442. Представьте в виде степени с основанием а

а) а ^па ^з; б) аа ^т; в) а ^га ^т; Г) (а2)Т; е) (азу •

443. Представьте в виде степени с основанием 5 число:

а) 25 ⁴; 6) 125 ³; в) 625 ².

444. • Представьте число 2 ²⁰в виде степени с основанием:

в) 2 ⁵; Г) 210

445. Запишите число 2 ⁶⁰в виде степени с основанием:

г) 32.

1 06

445. Выражение а ¹²представьте в виде степени несколькими способами.

446. Известно, что а²= т. Найдите а^б.

447. Упростите выражение:

а) х^з• (х²)⁵,	в) (а²)³• (а⁴)²,	д) (т²т³)⁴,
б) (а^зу • а⁵,	г) (х²)⁵• (х ⁵)²,	е) (х4х)2.

448. Запишите в виде степени с основанием а выражение:

а) (а²)⁴, в) (а5)2 • (а2)2,

б) а^з• (а^зу; г) (а^зу • (а^з

449. Упростите выражение:

а) х⁵• (х²)³, в) (х⁴)²• (х⁵)³,

б) (х³)⁴• х⁸, г) (х²)³• (х³)⁵,

д) (а³а ³)²,

е) (аа6)3.

д) (х3)2 (х4)5.

е) (х ⁷) ³

450. Найдите значение выражения:

2 ⁵• (2 ³)⁴(25)2 (52)4 . 25 311 . 27

а)в) д)ж)

2132 ⁶, 4' 59

(58)2 . 57 3⁷. 27 (73)3 . 72 (112)3

107

6) 522 г) (34)3 ; (75)2 з) 11². 11³

451. Известно, что а < О и Ь > О. Сравните с нулём значение выражения:

а) ан; в) a²b;

б) а^з», г) ан;

452. Какой цифрой может оканчиваться:

а) квадрат натурального числа;

б) четвёртая степень натурального числа?

453. Известно, что график функции у = Кх + 5,4 проходит через точку А (3,7; —2). Найдите значение коэффициента К.

454. На рисунке 59 построен график некоторой функции. Используя график, найдите:

а) значение у при х, равном —2;

б) значения х, при которых у равно —0,5; 2. Рис. 59

ё ее

Контрольные вопросы и задания

Сформулируйте определение зателем. Приведите примеры и ние и показатель степени.

Сформулируйте и докажите основное Сформулируйте правило умножения основаниями. Представьте в 12 • 12 ³• 12 ⁶

Сформулируйте правило деления ваниями. Представьте в виде дайте определение степени числа

Сформулируйте правило возведения

правило возведения в степень пени выражение: (5ab) ⁴; (а ^зу; у ⁴•

числа с натуральным поканазовите в каждом из них основа-

свойство степени.

степеней с одинаковыми виде степени произведение

степеней с одинаковыми осночастное 5,7 ⁶: 5,7 ³

с нулевым показателем.

в степень произведения, степени. Представьте в виде сте(у ²) ⁶.

ОДНОЧЛЕНЫ

21 . Одночлен и его стандартный вид

х•ыв-« м..нд

Выражения 5а ²х, 2b ³(—3) bc ², —3а ⁷, ху ²являются произведениями чисел, переменных и их степеней. Такие выражения называют одночленами. Одночленами считают также числа, переменные и их степени. Например, выражения 4 — одночлены.

Упростим одночлен 2b ³(—3) bc ², воспользовавшись переместительным и сочетательным свойствами умножения:

2Ь ^З = 2 Ь ^ЗЬс ²— --6b ⁴c ²

Мы представили одночлен 2b³(—3) bc ²в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных. Такой вид одночлена называют стандартным видом. К одночленам стандартного вида относят и такие одночлены, как —5, а, —а, а ^з. К стандартному виду можно привести любой одночлен.

Числовой множитель одночлена, записанного в стандартном виде, называют коэ?фициентом одночлена. Например, коэ$фициент одночлена —6b ⁴c равен —6. Коэффициенты одночленов а и —ab равны соответственно 1 и —1, так как а ²— 1 • а ²и —ab —1 • ab.

108	Глава lll

В одночлене 7ах ²у ³сумма показателей степеней всех переменных равна 6. Эту сумму называют степенью одночлена 7ах ²у ³. Степень одночлена — 9b ⁴c ³равна 7, степень одночлена —х ⁵равна 5.

Степенью одночлена всех входящих в него жит переменных и является степень этого одночлена

называют сумму показателей степеней переменных. Если одночлен не содерчислом, отличным от нуля, то считают равной нулю.

Число О является одночленом, степень которого не определена.

455. Является ли одночленом выражение:

а) 3,4х ²у;	г) х ²+ х;		к) с ¹⁰,
6) -0,7ху ²;	д) х ²х;	з) 2(х + у) ²,	л) —т ^о,
в) а (—0,8);	е) т3пт2,	и) —0,3ху ²;	м) 0,6?

456. Записан ли в стандартном виде одночлен:

а) бху; в) 0,5m • 2n; д) —х ²у ³,

б) —2aba; г) —bca; е) 5р ³р ²?

457. Представьте одночлен в стандартном виде и назовите его коэффициент:

а) 8х ²х; в) 3ху (—1,7) у;

б) 1,2abc • 5а; г) 6с ²(—0,8) с;

458. Приведите одночлен к стандартному виду:

а) 9уу ²у; в) —8ab (—2,5) b ²; д) 2т ^Зп • 0,4mn;

б) 0,15pq • 4pq ²; г) 10a ²b ²(—1,2а ³); е) —2х ³• 0,5ху ².

459. Найдите значение одночлена:

а) —0,125у ⁴при у = —2; б) 12х ²у при х = —0,3, у = —

460. Вычислите значение выражения:

а) 3,7m ²при т = 0,4; б) —3a ³b при а , ,

461. Ширина прямоугольника равна т см, а длина в 5 раз больше ширины. Найдите площадь прямоугольника.

462. Чему равен объём прямоугольного параллелипипеда, ширина которого а см, длина в 2 раза больше ширины, а высота в 2 раза больше длины?

109

5 8.

463. Какова степень одночлена:

а) —7х ⁵у⁶; в) 0,8mn ³k ²;

б) —abc; г) аЬ ²с ³;

д) —6m ⁷;

464. Найдите координаты точки В, симметричной точке А (—7; 15) относительно: а) оси х; б) оси у; в) начала координат.

2 465. Функция задана формулой у = —— х. Найдите значение функЗ

2 2

ции при х = —3; З; — • 2,4. При каком х значение у равно 3'

1; -6; -10,2?

466. Найдите значение выражения: а)6)

22. Умножение одночленов, Возведение одночлена в степень

При умножении одночленов и возведении одночлена в сте- I пень используются правило умножения степеней с одинаковыми основаниями и правило возведения степени в степень. При этом получается одночлен, который обычно представI ляют в стандартном виде.

Пример 1. Перемножим одночлены —5a ²bc и 4a ²b ⁴

Составим произведение этих одночленов. Перемножим их числовые множители и степени с одинаковыми основаниями.

Получим

—5а ²Ьс • 4a ²b ⁴= (—5 • = —20a ⁴b ⁵c.

Пр имер 2. Найдём произведение одночленов —х ²у, 4х ³у ²и —5ху. —х ²у • 4х ³у ²• (—5ху) = —1 • 4 • (х ²х ³х) (уу ²у) = 20х⁶у ⁴.

Пример З. Возведём в третью степень одночлен —2a ²b.

Воспользуемся правилами возведения в степень произведения и степени:

(-2а ²Ь) ^З= (—2) ³(а ²)³Ы = —8a ⁶b ³.

Пример 4. Возведём одночлен —х ^зу ²в четвёртую степень. Имеем (—хЗу2)4 = (—1)4 • (х3)4 • (у2)4 х12у8.

1 10	Глава lll

467. Выполните умножение:

в) —ab ³• !ab• 2

б) —8х • 5х ³; г) х ²у ⁵• (—6ху ²);

468. Перемножьте одночлены:

д) —0,6a ²b • (—10ab ²);

е) ——m ³n ⁴• 5m ²n ³.

а) —11х ²у и 0,3х ²у ²; в) 4ху, —х ²и —у^з,

б) a ⁵b и —ab ³c; г) а ²х ⁵Ь, —0,6axb ²и 0,6a ²b³

469. Выполните умножение:

а) 3,5 • Зт; г) ab • (—7ab ²) • 4a ²b;

б) —6ах ^З• 9bx ²; д) 10х ²у • (—ху²) • 0,6х ³;

в) —8a ²b ²• (—8a ³b ⁵); е) —9ab ²• За ^з• (—4b).

470. Представьте несколькими способами одночлен 6a ²b ³в виде произведения двух одночленов стандартного вида.

471. Представьте одночлен —12х ⁴у³двумя способами в виде произведения:

а) двух одночленов стандартного вида;

б) трёх одночленов стандартного вида.

472. Выполните возведение в степень:

а) (3х2)3; в) (—2a4b2)3; д) (—a ²bc ³) ⁵;

г) (—3х ²у) ⁴; е) (—a3b2c)2

473. Представьте в виде одночлена стандартного вида:

а) (2m3)4; д) (—xy4b2)4.,

г) (—2хуЗ)2; е) (—х2у3т)5.

474. Возведите одночлен:

а) 5х ²у³в квадрат; в) —2m ³n ²в четвёртую степень;

б) —4ах ³в куб; г) —a ²bc ³в пятую степень.

475. Представьте выражение в виде квадрата одночлена:

а) 81х⁴; 6) 1210 ⁶; В) 0,09y ¹²; г) —b ⁶.

476. Представьте выражение в виде куба одночлена:

а) 64х ⁹; 6) О,ОО1у ¹²; в) -0,0088; Г) ——a ¹⁵27 477. Представьте каждый из одночленов:

а) 9b ²c ², 100m ²n ⁶в виде квадрата одночлена;

б) --a ³b⁶—27х ⁶Ь ⁹в виде куба одночлена.

478. Запишите каждый из одночленов:

а) 16х ⁶, 49m ²n ⁴и т ⁸в виде квадрата одночлена;

б) а ⁹, —8m ³и 1000х ³у ⁶в виде куба одночлена.

1 1 1

ё 8.

479. Какой одночлен надо возвести в квадрат (в куб), чтобы получить одночлен: а) х 6 у12. б) 1 ООО ОООт18?

480. Представьте выражение в виде одночлена стандартного вида:

а) 25а⁴• (За³) ²;	д) (-10с ²)⁴• 0,00018 ¹;
6) (-3b⁶) ⁴• Ь;	е) (3b5)2 • — Ы. 9
в) 8p15 • (—Р)4;	1 ж) (—2х3)2 . 4
г) (-8) ³• 0,158;	з з) 2

481. На одном складе было 185 т угля, а на другом — 237 т. Первый склад стал отпускать ежедневно по 15 т угля, а второй — по 18 т. Через сколько дней на втором складе угля будет в полтора раза больше, чем на первом?

Прямая, являющаяся графиком функции, заданной формулой у = Кх + Ь, пересекает оси координат в точках А (О; 6) и В(—4; О). Найдите К и Ь.

483. Точка А (а; —3) симметрична точке В(4; Ь) относительно: а) оси абсцисс; б) оси ординат; в) начала координат. Найдите значения а и Ь.

23. Функции у = х ²и у х ³и их графики

Зависимость площади квадрата от его стороны и зависимость объёма куба от его ребра являются примерами функций, которые задаются формулами вида у = х²и у = х^з.

Построим график функции у = х². Составим таблицу соответственных значений х и у:

х						-0,5	о		1	1,5	2	2,5	з
		6,25	4	2,25	1	0,25	о	0,25	1	2,25	4	6,25	9

Построим точки, координаты которых указаны в таблице (рис. 60). Чтобы точнее построить график вблизи начала координат, вычислим ещё несколько значений функции:

	—0,4	-0,3	-0,2	-0,1	0,1	0,2		0,4
У	0,16	0,09	0,04	0,01	0,01	0,04	0,09	0,16

1 1 2	Глава lll

Рис. 60 Рис. 61

Из таблицы видно, что при значениях х близких к нулю значения функции мало отличаются от нуля. Значит, график функции вблизи начала координат почти сливается с осью х.

Через отмеченные точки проведём плавную линию (рис. 61). Получим график функции у = х ².

Ясно, что график функции у = х ²неограниченно продолжается вверх справа и слева от оси у.

График функции у = х ²называют параболой.

Выясним некоторые свойства функции у = х ².

5 8.

1. Если х = О, то у = О. Поэтому график функции проходит через начало координат.

2. Если х О, то у > О. Действительно, квадрат любого числа, отличного от нуля, положителен. Значит, все точки графика функции, кроме точки (О; О), расположены выше оси х.

I З. Противоположным значениям х соответствует одно и то же значение у. Это следует из того, что (—х) ²= х ²при любом х, Значит, точки графика, имеющие противоположные абсциссы, симметричны относительно оси у.

Построим теперь график функции у = х ^з. Составим таблицу соответственных значений х и у, округляя значение у до сотых:


У	—8	-3,38	-1	-0,13	о	0,13	1	3,38	8

1 14	Глава lll

Построим точки, координаты которых указаны в таблице (рис. 62). Через отмеченные точки проведём плавную линию (рис. 63). Получим график функции у = х ^з. Ясно, что этот график неограниченно продолжается справа от оси у вверх и слева от оси у вниз.

Заметим, что вблизи начала координат график функции почти сливается с осью х (если х = 0,2, то у = 0,008; если х = 0,3, то у = 0,027).

Выясним некоторые свойства функции у = х ^з.

1. Если х = О, то у = О. Поэтому график функции проходит через начало координат.

2. Если х О, то у > О; если х < О, то у < О. Действительно, куб положительного числа есть число положительное, а куб отрицательного числа есть число отрицательI ное. Значит, график функции расположен в первой и третьей координатных четвертях.

З. Противоположным значениям х соответствуют противоположные значения у. Это следует из того, что при любом значении х верно равенство (—х) ³= --х^з. Значит, точки графика, имеющие противоположные абсциссы, расположены симметрично относительно начала координат.

С помощью графиков функций у = х? и у = х ^зможно найти приближённые значения корней некоторых уравнений. Приведём примеры .

闣圞

·圞

圝圝豳圞酺匴臺•圝筮

圝'圝

圝圞圞鯔 -圝

靆諈醺圝鐆圝圝圝

十

4-+

c. 62

1 1 5

·镾匴·

圝圝敻鼲圞圝

圛·

醢讔驨蠱

對'圝圝圝

歰蠱闣圝黫熟鍙圞

c· 63

§ 8. OAHOqneHbl

Рис. 64

Пример 1. Решим уравнение .r ²= х + 1. Построим в одной системе координат графики функций у = .r ²и у = х + 1 (рис. 64). Эти графики пересекаются в двух точках. Абсциссы точек пересечения графиков являются теми зна- Рис. 65 чениями переменной х, при которых выражения х ²и х + 1 принимают равные значения. Значит, абсциссы точек пересечения являются корнями уравнения х ²= х + 1. Из рисунка видно, что это уравнение имеет корни —0,6, Х2 1,6.

Пример 2. Решим уравнение х ^з= 3х.

Построим в одной координатной плоскости графики функций у в трёх = х ^зточках. и у = 3х Уравнение (рис. 65). х Графики = 3х имеет этих три функций корня: — пересекаются1,7, О и 1,7.

Заметим, что число О является точным значением корня, а числа —1,7 и 1,7 — приближёнными.

Итак, мы нашли, что

—1,7, Х2 = о, Х— 1,7.

Применённый нами способ решения уравнений называется графическим.

484. Используя график функции у = х ², изображённый на рисунке 61, найдите:

а) значения у, соответствующие х 0,75; —1,25; 1,25; —2,2; 2,2;

б) значения х, которым соответствует у = З; 5.

1 16	Глава llI

485. Пользуясь графиком функции у = х²(см. рис. 61), найдите: а) значение функции, соответствующее значению аргумента, равному 1,4; —2,6; 3,1;

б) значения аргумента, при которых значение функции равно 4; 6;

в) несколько значений х, при которых значения функции меньше 4; больше 4.

486. Воспользовавшись графиком функции у = х ², изображённым на рисунке 61, найдите:

а) значение у, соответствующее х = —2,4; —0,7; 0,7; 2,4;

б) значения х, которым соответствует у = 2; 0,9;

в) несколько значений х, при которых значение функции больше 2; меньше 2.

487. Принадлежит ли графику функции у = х ²точка:

а) „4(6•, 36); 6) щ-1,5; 2,25); в) се; г) 1,44)?

488. Используя график функции у = х^з(см. рис. 63), найдите:

а) значение у, соответствующее х = 1,4; —1,4; —1,8; 1,8;

б) значение х, которому соответствует у

489. Пользуясь графиком функции у = .r ³(см. рис. 63), найдите: а) значение функции, соответствующее значению аргумента, равному —0,7; 1,2;

б) значение аргумента, которому соответствует значение функции, равное З; —3;

в) несколько значений аргумента, при которых значение функции больше —3, но меньше З.

490. Принадлежит ли графику функции у = х^зточка:

а) -0,008);

491 В одной и той же системе координат постройте графики функций у = х ²и у = х ^з, где х > О. Пользуясь построенными графиками, сравните: а) 0,6 ²и 0,6 ³; б) 1,5 ²и 1,5 ³; в) 2,7²и 2,7 ³

492. При каких значениях а точка Р (а; 64) принадлежит графику функции: а) у = х ²; б) у = х ³?

493. (Для работы в парах.) Используя график функции у х², изображённый на рисунке 61, решите уравнение:

а) х ²= 4; в) х²= 5;

1) Распределите, кто выполняет задания а), б), а кто — задания в), г), и выполните их.

2) Проверьте друг у друга правильность выполнения заданий. З) Сделайте вывод о числе корней уравнения х ²= а при различных значениях а.

ё 8. одночлены

494. Решите графически уравнение:

6) х²+ 2х - 3 = 0.

495. (Для работы в парах.) Используя график функции у = х^з, изображённый на рисунке 63, решите уравнение:

в) х³= 5;

г) х³= О.

1) Распределите, кто выполняет задания а), г), а кто — задания б), в), и выполните их.

2) Проверьте друг у друга, правильно ли выполнено задание. З) Сделайте вывод о числе корней уравнения х^з= а при различных значениях а.

496. Решите графически уравнение:

497. Сравните значения выражений:

а) 0,3 ¹⁶и г) (—1,4)⁶и —1,4 ⁶; 6) и 1,9 ²¹; д) —64 и —2 ⁶;

в) —5,6 ⁴и (—5,6)⁴; е) -0,8 ¹¹и

498. Не выполняя построения, найдите координаты точки пересечения графиков функций у = 8,5х и у = 0,5х — 19,2.

499. Упростите выражение:

а) —0,6a³b (—2a ²b³)³• г) (7х²у) ²

б) 0,8ху ⁴(—6ху⁴)²; д) (—ас)6 • (—2а2с)5;

в) —a⁴b ⁷(—3ab)²; е) 3p²q •

Контрольные вопросы и задания

Приведите пример одночлена

Представьте в стандартном виде те его коэффициент.

Сформулируйте определение степени мер одночлена пятой степени. Сформулируйте свойства функции свойства на графике функции у = Сформулируйте свойства функции свойства на графике функции у =

стандартного вида.

одночлен 5ab²• (—3аЂ) и укажи-

одночлена. Приведите при-

у = х ². Как отражаются эти х²?

у = х^з. Как отражаются эти х³?

1 18	Глава lll

Для тех, кто хочет знать больше

24. О простых и составных числах

Напомним известные вам определения простого и составного числа. Натуральное число называется простым, если оно имеет только два натуральных делителя: единицу и само это число. Натуральное число называется составным, если оно имеет более двух натуральных делителей. Число 1 не является ни простым, ни составным числом.

Выпишем в порядке возрастания простые числа, входящие в первую сотню натуральных чисел. Получим

2, з, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,

43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

В настоящее время составлены таблицы, содержащие миллионы простых чисел. Естественно встаёт вопрос, существует ли наибольшее простое число. Ответ на этот вопрос ещё в III в. до н. э. дал великий греческий математик Евклид, который доказал, что «простых чисел больше, чем любое их число», т. е. бесконечно много.

Проведём соответствующее доказательство. Допустим, что существует наибольшее простое число р. Составим произведение всех простых чисел от 2 до р включительно и обозначим его через а:

а = 2 - 3 - 5

Рассмотрим число а + 1:

а + 1 =2 . 3 - 5

Число а + 1 не является простым, так как оно больше р, а по предположению р — наибольшее простое число. Оно не является также составным, так как по свойству делимости суммы не делится ни на одно из простых чисел, входящих в произведение 2 • З • 5 а других простых чисел по предположению нет. Полученное противоречие показывает, что предположение неверно и наибольшего простого числа не существует.

Много раз делались попытки найти какое-либо выражение, значениями которого являются только простые числа. Рассмотрим, например, выражение Р (п) = 2n ²+ 29. Вычисляя его значения при найдём, что F(1) = З, F(2) = 37, F(3) = 47, F(4) = 61, F(5) = 79, F(6) = 101, F(7) — - 127. Мы видим, что каждый раз получается простое число. Можно предположить, что значение выражения Е (п) при любом натуральном п является простым числом. Однако это не так. Например, число Р (29) = 2 • 29 ²+ 29 не является простым, так как из свойства делимости суммы следует, что оно делится на 29. Вообще, доказано, что не существует многочлена F(n) с целыми коэффициентами, значением которого при любом натуральном п является простое число.

1 19

для тех, кто хочет знать больше

Всякое составное число, как известно, можно представить в виде произведения простых чисел или, как говорят, разложить на простые множители и притом единственным способом, если не учитывать порядок множителей. Разложим, например, на простые множители число 360:

360 = 2 .

= 2 . 2 - 2 - 3 - 15 = 2 - 2 - 2 - 3 - 3 - 5.

При разложении числа на простые множители произведение одинаковых множителей обычно представляют в виде степени: 360 = 2 ³• 3 ²• 5.

Разложением чисел на простые множители удобно пользоваться при нахождении их наибольшего общего делителя или наименьшего общего кратного.

Найдём, например, наибольший общий делитель и наименьшее общее кратное чисел 504 и 2352. Разложив каждое из этих чисел на простые множители, получаем, что

504 = 2 ³• • 7 и 2352 • з . 7 ²

Чтобы найти наибольший общий делитель этих чисел, надо каждый из множителей взять в степени с наименьшим показателем, с каким он входит в эти числа, а чтобы найти их наименьшее общее кратное — с наибольшим показателем.

Обозначив через d наибольший общий делитель этих чисел, а через К их наименьшее общее кратное, получаем, что . з . 168, к = . 3 ². 7 ²= 7056.

П р им е р. Наименьшее общее кратное двух чисел равно 96. Одно из этих чисел — число 6. Каким может быть другое число?

Разложив числа 96 и 6 на простые множители, получаем, что

Очевидно, что в разложение искомого числа на простые множители должны входить пять двоек и не более одной тройки. Значит, второе число либо равно 2 ⁵, т. е. 32, либо равно 2 ⁵З

т. е. 96.

500. Если в выражении а ²+ а + 17 подставлять вместо а числа О, 1, то сначала получаются простые числа. Укажите наименьшее натуральное значение а, при котором значение этого выражения является составным числом.

Докажите, что значение выражения является составным числом:

а) 15 ⁹+ 31 ³; 6) 16 ⁷+ 25 ⁵- 41 ⁴

120	Глава lll

Найдите наибольшее двузначное число, равное произведению двух простых чисел.

Пусть р — простое число. Укажите наименьшее значение р, при котором значение выражения 2^Р— 1 не является простым числом.

Найдите все простые числа, на которые делится сумма:

а) 2 + 2 ²+ 2³+ 2 ⁴; б) 5 + 52 + 53 + 54

505. Разложите на простые множители число: а) 5082; б) 7605.

Разложите на простые множители число а, если а = 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10.

507. Найдите наибольший общий делитель чисел:

а) 765 и 315; 6) 792 и 1936.

508. Найдите наименьшее общее кратное чисел:

а) 294 и 756; 6) 693 и 1617.

В последовательностях записаны в порядке возрастания все натуральные числа, которые не превосходят 200, причём в первой последовательности записаны числа, кратные 6, а во второй — кратные 8:

6, 12, 18

8, 16, 24

Сколько в этих последовательностях одинаковых чисел?

510. Какой цифрой оканчивается значение выражения:

а) 45 ⁵— 31 ⁴; 6) 37²+ 21 ⁶+ 45⁴?

Дополнительные упражнения к главе Ш

К параграфу 7

511. Верно ли равенство:

а) 3²+ 42 + 52 = 62. = 13 + 23 + 33 + 43? Докажите, что 26 ⁷+ 15 ⁵— 11 ⁹кратно 10.

513. Разложив число на простые множители, представьте его в виде произведения степеней простых чисел:

в) 225; г) 500.

514. Представьте число в виде степени с основанием 2 или З:

а) 64; б) 81; в) 512; г) 729; д) 1024.

515. Представьте число в виде суммы степеней числа 2: 6) 18; в) 42.

1 21

516. Представьте число в виде степени с показателем, отличным от 1:

а) 121; 6) -32; в) 0,125; г) 625 -0,216;

517. Найдите значение выражения:

а) 0,001х ²при х = —2; в) х ²у ⁴при х = 5, у 2

б) 1000у ³при у = 0,1; г) 3х ³у ³при х = —

518. Найдите значение выражения (—1) ^ппри п, равном: 6) 11; в) 23; г) 70. 519. Вычислите:

а) сумму кубов чисел 5 и —3;

б) куб суммы чисел 9 и —11;

в) разность квадратов чисел 12 и 8;

г) квадрат разности чисел 96 и —4;

д) удвоенное произведение квадратов чисел 7 и —5;

е) утроенное произведение числа 15 и квадрата числа 4.

520. Не выполняя вычислений, сравните значения выражений:

б) О и (—1,25) ⁷; г) 0,98 ⁶и 1,02 ⁶

521. Что больше и на сколько:

а) 2 ³или 3 ²; в) 2 • 3 ²или З • 2 ³;

б) 5 ²или 2 ⁵; г) (11 + 19) ²или 11 ²+ 19 ²?

522. Сравните значения выражений а ²и а ^зпри а, равном:

а) -12;

523. Найдите при х = 1,5 и х = —2 значения выражений:

а) х ², б) х ^з,

[524] Докажите, что при любом натуральном п значение дроби является натуральным числом:

10П - 1

а) 6)в)

9 9 З

525. Какие из чисел —3, —2, —1, 1, 2, З являются корнями уравнения:

д) .r ³— 3х ²— 4х + 12 = О;

6) г) .r⁴+ .r ³= 6х ²е) х ^з+ 3х ²- х - 3 = 0?

526. Докажите, что не имеет корней уравнение:

б) 2х ⁶+ 3х ⁴+ .r ²+ 1 = О.

527. При каком значении х значение выражения (2х + равно нулю?

528. Докажите, что уравнение х ⁴+ 3х ³+ 2х ²+ х + 6 = О не имеет положительных корней.

529. Имеет ли уравнение .r ⁶— .r ⁵+ х ⁴— .r ³+ .r ²— х + 1 = О отрицательные корни?

1 22	Глава lll

530. Упростите выражение:

а) а 10 а 12(—а5); б) Х (—Х) (—х ^б); в) у^Ку⁸у ², г) Ь ^ПЬ ^ПЬ ^З

531. Представьте выражение в виде степени:

а) 2 ⁵• 8; 6) 16 • 64; в) • 343; г) 81 • з ^к

532. Представьте выражение в виде произведения двух множителей, один из которых равен а ⁵: а) а10. б) аб; в) —а40.

533. Замените х степенью с основанием с так, чтобы полученное равенство было тождеством:

	а) с ²х = с ⁵, б) хс ⁵— с⁹,	в) с ^бх = с ^и,	г) с⁴х = с ¹⁵.
534.	Замените частное степенью:
	а) b15 : b12. б) 739 : 713.	в) а ¹¹	г) : 12 ⁹⁹
535.	Найдите значение выражения:
	а) 13 ¹⁰⁰: в) 2 ¹⁴: 8 ⁴'	д) 5 ¹⁰: 25 ⁴;
	3 ⁸. 2⁷95 • 59	38. 58

6) 3 ⁶. 2 ⁵' г) 3⁹• 310 . 57 •

536. Упростите выражение:

6) : 10 ^п- ¹

537. Вычислите:

а) (217 - 43,07 • 5) ⁰+ 5 . 6) 17,83 ⁰

3' 7 538. Упростите:

б) (—1)2п : (-1)3.

539. Площадь круга вычисляется по формуле S = ПР, где — радиус круга. Как изменится площадь круга, если его радиус увеличить в З раза? в 7 раз?

4 540. Объём шара вычисляется по формуле V = — 7tr , где r — радиус З шара. Как изменится объём шара, если радиус увеличить в 2 раза? в 4 раза?

541. Верно ли при любом значении х равенство:

а) 1 хр = х ²,

542. Найдите значение выражения:

а) 4 ⁵• 2,5 ⁵;	в) 0,2 ⁹• 5 ⁷•	д) 0,2 ⁶• 253;
13 1		6 1
6) • 313.	г) 0,4 ¹⁰• 2,5 ¹²•	• 814
з		9

543. Сравните значения выражений:

а) 10 ⁷и 2 ⁸• 5 ⁷• в) 25 ²⁵и 2 ⁵⁰• 3 ⁵⁰'

б) 6 ¹²и 2 ¹³• 3 ¹¹' г) 63 ³⁰и 3 ⁶⁰5 ³⁰

1 23

544. Представьте выражение в виде З ^аили

а) (—33)2., б) (—32)3; в) —(34)2.,

545. Упростите выражение:

а) (х ³) ²• (—х3)4, ( х2)6. 6) (-у3)7 • (-у4)5, г) (—с9)4 • (с5)2•

Замените букву р выражением так, чтобы полученное равенство было тождеством:

а) р ⁵= х ²⁰, б) р ⁷= .r ²¹; в) р ³с ⁸= с ²⁰, г) у 7 • (У2)4 = Р5•

547. Представьте в виде степени:

а) 4 ⁵• б) 2513 : 511. в) 8 ⁵• 16 ¹³; г) 2710 : 915

548. Представьте выражение в виде х ^пили —х ^п:

3)7. 2)5. в) (—х) ⁴х ⁸,

Сколькими способами можно представить в виде степени с показателем, отличным от 1, число:

а) 215.

При каком условии:

а) сумма квадратов двух чисел равна нулю;

б) квадрат суммы двух чисел равен нулю?

Натуральное число а оканчивается единицей. Какой цифрой оканчивается степень числа а с натуральным показателем? Для каких ещё цифр выполняется аналогичное свойство?

Докажите, что при любом натуральном К:

а) число 3 ^4kоканчивается единицей;

б) число 10 ^k— 1 кратно З.

К параграфу 8

553. Какова степень одночлена:

а) зх^зу ⁷; в) a ⁹b ⁹; д) —8х⁰;

б) —10ab ²c ³• г) —xyz; е) 2,4?

554. Представьте выражение в виде одночлена стандартного вида и укажите его степень:

а) 5ab • 0,7bc • 40ас; в) —a ³b • За ²Ь ⁴;

6) -0,45bd • —1 — ad • 9ab; г) 0,6х ³у • (—0,5ху ³).

555. Составьте все возможные одночлены стандартного вида с коэффициентом 5, содержащие переменные х и у, такие, что степень каждого одночлена равна:

а) трём; б) четырём.

124	Глава lll

556. Представьте выражение в виде произведения двух одночленов стандартного вида, один из которых равен 20х ⁴у:

а) 100х ⁵у ³; в) —4х ¹⁶у; д) 5х⁸у;

б) —30х⁴у ⁵; г) х10У2' е) —х4у2.

557. Представьте данный одночлен в виде произведения двух каких-нибудь одночленов стандартного вида:

а) —8а ⁵с ³; б) —b ⁶y⁹; в) 60х ¹⁰у ¹⁵

558. Преобразуйте выражение в тождественно равный одночлен стандартного вида:

а) (—10ab12)2; в) (—3ху ²а ³) ³;

559. Представьте произведение одночленов в виде степени некоторо-

го одночлена:

а) 27a ²b ⁵• За ^1ОЬ ^З•

б) —64а ⁸х ¹¹• (—0,258х⁹);

560. Упростите выражение:

а) (—х ²у ²) ⁴• (—ху) ²,

1 ^зз.

6) — ху з

в) (—2х3у2)3 .

1 г) —a ²b • (9ab ²) ²• З

д) (—5a ³b) ²

—— ab4

в) 0,01b5c3 • (—0,1bc⁶);

9 з

г)p9q14 - p³q ⁴

ж) (х ^Зу) ²• 5ху) ³;

1 з) — х ²у ²• (—12х ³у ⁵

561. Представьте выражение в виде произведения числа З и квадрата некоторого выражения:

а) Зт ⁴п ²; б) 12x⁶y ⁴z ²; в) —т ⁸п⁴.

562. На рисунке 66 построены графики функций у = х, у = х², у = х ^з, где х > О. Пользуясь графиком, срав-

ните:

а) 0,23 и 0,23 ²; 6) 1,47 и 1,47 ²; 0,23 и 0,23 ³; 1,47 и 1,47 ³;

0,23 ²и 0,23 ³; 1,47 ²и 1,47 ³.

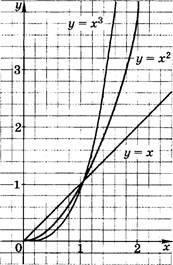
Рис. 66

1 25

563. а) Известно, что точка Р (—4; Ь) принадлежит графику функции, заданной формулой у = х². Найдите значение Ь. Принадлежит ли графику этой функции точка Q(4; Ь)?

б) Известно, что точка А (—4; а) принадлежит графику функции, заданной формулой у = х^з. Найдите значение а. Принадлежит ли графику этой функции точка В (—4; —а)? [Q] Точка А (а; Ь) принадлежит графику функции:

а) у = х², б) у = х^з.

Принадлежат ли этому графику точки В (—а; Ь), С (а; —b),

Расположите в порядке возрастания числа а, а ²и а ^з, если:

в)

566. Решите графически уравнение:

г)

126	Глава lll

В этой главе вы познакомитесь с многочленами — одним из важнейших видов выражений с переменными. Вы научитесь выполнять сложение, вычитание и умножение многочленов, использовать эти преобразования для упрощения выражений. Вы узнаете о таких приёмах разложения многочленов на множители, как вынесение множителя за скобки и способ группировки. Изученные преобразования вы сможете широко применять при решении уравнений, доказательстве тождеств, в задачах на делимость. В этой главе значительно расширяется круг ТеКСТОВЫХ задач, решаемых с помощью уравнений. Надеемся, что вас заинтересуют задачи на смеси и сплавы, с которыми вы неоднократно будете встречаться в курсах физики и химии.

МНОГОЧЛЕНОВ

25. Многочлен и его стандартный вид

127

Выражение 4х ²у — 5ху + 3х — 1 представляет собой сумму одночленов 4х ²у, —5ху, 3х и —1. Такие выражения называют многочленами.

Одночлены, из которых составлен многочлен, называют членами многочлена. Так, членами многочлена 4х ²у — 5ху + 3х — 1 являются одночлены 4х ²у, —5ху, 3х и —1.

Если многочлен состоит из двух членов, его называют двучленом; если из трёх членов — трёхчленом. Одночлен считают многочленом, состоящим из одного члена.

•м-ш.». ..дмет

В многочлене 5a ²b + 2 + 4ab ²— За ²Ь — 7 члены 5a ²b и —3a ²b являются подобными слагаемыми, так как они имеют одну и ту же буквенную часть. Подобными слагаемыми являются и члены 2 и —7, не имеющие буквенной части. Подобные слагаемые в многочлене назыВаог подобными членами многочлена, а приведение подобных слагаемых в многочлене — привеДением подобных членов многочлена.

Пример 1. Приведём подобные члены в многочлене 5а ²Ь + 2 + 4аЬ ²- за ²ь - 7.

Имеем

5а ²Ь + 2 + 4аЬ ²- - 7 = (5а ²ь - + 4аЬ ²+ (2 - 7) = — 2a ²b + 4ab ²— 5.

Каждый член многочлена 2a ²b + 4ab ²— 5 является одночленом стандартного вида, и этот многочлен не содержит подобных членов. Такие многочлены называют многочленами стандартного виДа.

Любой многочлен можно привести к стандартному виду. Для этого нужно каждый его член представить в стандартном виде и привести подобные члены.

Членами многочлена стандартного вида 8ху + 6х ²у ³— 9 служат одночлены второй, пятой и нулевой степеней. Наибольшую из этих степеней называют степенью многочлена. Таким образом, многочлен 8ху + 6х ²у ³— 9 является многочленом пятой степени.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

Пример 2. Определим степень многочлена За ⁴+ 8ab — 2а ⁴— а ⁴+ 56. Для этого приведём его к стандартному виду:

За ⁴+ 8ab — 2а ⁴— а ⁴+ 56 = 8ab + 56.

Степень многочлена 8ab + 5b равна двум, поэтому степень многочлена За ⁴+ 8ab — 2а ⁴— а ⁴+ 5b также равна двум.

567. Назовите каждый член многочлена:

а) —6х ⁴+ у ^з— 5у + 11; б) 25ab + ab ²— a ²b + 8а — 76.

568. Приведите подобные члены многочлена:

а) 10х — 8ху — 3ху; в) 3х ⁴— 5х + 7х ²— 8х ⁴+ 5х;

б) 2ab — 7ab + 7а ²; 20 ³+ - 17 - За ²+ - а - 80.

128

569. Из данных многочленов выберите многочлен, тождественно равный выражению За ²+ Ь.

1. 4а ²— 46 — а ²+ 176 — Ь з. - - 98 + 66 + ь

2. -0,78 - 76 - 2,38 + 8b 4. 1,88 - 4,2b+ 1,28 + + 0,2b

570. Представьте в стандартном виде многочлен:

а) —8р ⁴+ 12р ³+ 4р ⁴— 8р ²+ Зр ²;

б) 2аа ²+ а ²— За ²+ а ^з— а;

в) 3хх ⁴+ 3хх ³— 5х ²х ³— 5х ²х;

г) За • 46 ²- 0,8b • - 2аь • • ЗУ - 1

571. Запишите в стандартном виде многочлен:

а) 2а ²х ³— ах ^з— а ⁴— а ²х ³+ ах ^з+ 2а ⁴;

б) 5х • 2у ²— 5х • 3ху — х ²у + 6ху ².

572. Найдите значение многочлена:

а) 5х ⁶— 3х ²+ 7 — 2х⁶— 3х ⁶+ 4х ²при х = —10,

б) 4a ²b — ab ²— За ²Ь + ab²— ab + 6 при а ,

573. Найдите значение многочлена:

а) ба ^з— а ¹⁰+ 4а ³+ а10 — 8а3 + а при а = —3,

б) 4х ⁶у ³— 3х ⁶у ³+ 2х ²у ²— х ⁶у ³— х ²у ²+ у при х = —

129

574. Найдите значение многочлена 2х ²+ 1 при х = О; —2; З; —4. Существует ли такое значение х, при котором значение многочлена равно нулю? отрицательно?

575. Докажите, что многочлен х ²+ у ²+ 1 при любых значениях х и у принимает положительные значения.

576. Запишите в виде многочлена число, состоящее из:

а) с десятков и Ь единиц;

б) а сотен, Ь десятков и с единиц.

577. Расположите члены многочлена по убывающим степеням переменной:

а) 17а ⁴- + За - Ю - 1; б) 35 — с^б+ 5с ²— с ⁴

578. Расположите члены многочлена по возрастающим степеням переменной:

а) х⁴— 5 — х ²+ 12х;

579. Какова степень многочлена:

а) 4а ⁶— 2а ⁷+ а — 1; г) 4ху + ху ²— 5х ²+ у;

д) 8х ⁴у + 5х ²у ³— 11;

е) ху + yz + xz — 1?

580. Используя калькулятор, найдите значение многочлена:

а) х ²+ 4,23 при х = 1,97; б) а ⁴+ 2а при а = 2,3.

Макарычев, 7 кл.

581. (ЗаДача-исслеДование.) Докажите, что всякая разность вида abbb — а делится на 37.

1. Проверьте верность этого утверждения для разности:

а) 2555 - 2; 6) 7111 - 7; в) 8999 - 8; г) 9666 - 9.

2. Проведите доказательство высказанного утверждения.

582. Решите уравнение:

а) о,зу = 70; б)в)

583. Вычислите:

5³• 25²25. 8

а) б) в)

58 69

584. При каком значении аргумента функция у = 0,01х принимает значение, равное:

а) 240; 6) -100?

26. Сложение и вычитание многочленов

Сложим многочлены 5х ²+ 7х — 9 и —3х ²— 6х + 8.

Для этого составим их сумму, затем раскроем скобки и приведём в полученном многочлене подобные члены:

(5х ²+ 7х - 9) + (-3х ²- 6х + 8) =

5х ²+ 7х - 9 - 3х ²- 6х 2х ²+ х- 1.

Вычтем из многочлена х ^з+ 5х ²— х + 8 многочлен х^з— 7х — 1. для этого составим их разность, раскроем скобки и приведём в полученном многочлене подобные члены:

(х ^з+ 5х ²— х + 8) — (х ^з— 7х — 1) =

= хЗ + 5х2 — х + — + 7 х + = 5х2 + 6 х +

Мы представили сумму многочленов 5х ²+ 7х — 9 и —3х ²— 6х + 8

в виде многочлена

2х ²+ х — 1,

а разность многочленов х ^з+ 5х ²— х + 8 и х ³— 7х — 1 в виде много-

члена

5х2 + 6х + 9.

Вообще сумму и разность многочленов всегда можно представить в виде многочлена.

Иногда требуется решить обратную задачу — представить многочлен в виде суммы или разности многочленов. При этом пользуются правилом:

130	Глава lV

если перед скобками ставится знак «плюс», то члены, которые заключают в скобки, записывают с теми же знаками; если перед скобками ставится знак «минус», то знаки членов, заключаемых в скобки, меняют на противоположные.

Например:

585. а) Составьте сумму многочленов 4х ³— 5х — 7 и х ^з— 8х и преобразуйте её в многочлен стандартного вида.

б) Составьте разность многочленов 5у ²— 9 и 7у ²— у + 5 и преобразуйте её в многочлен стандартного вида.

586. Даны два многочлена: 2а ^з— 5а + 5 и а ^з— 4а — 2. Упростите:

а) сумму этих многочленов;

б) разность первого и второго многочленов;

в) разность второго и первого многочленов.

587. Преобразуйте в многочлен стандартного вида:

а) (1 + За) + (а ²— 2а);

б) (2х ²+ зх) + (—х + 4);

в) (у ²— 5у) + (5у — 2у ²);

г) (62 — Ь + 7) _ (62 + + 8);

д) (8n ³— Зп ²) — (7 + 8пз — 2n2);

е) (а ²+ 5а + 4) — (а ²+ 5а — 4).

588. Упростите выражение:

а) 5,2а — (4,5а + 4,88);

б) 8х ²+ (4,5 — х ²) — (5,4х ²- 1);

в) -0,88 + 7,4b + (5,6b - 0,28);

г) (7,зу - у ²+ 4) + о,5у ²- (8,7у - 2,0 ²).

589. Преобразуйте в многочлен стандартного вида:

а) 18х ²— (10х — 5 + 18х ²); в) (6 ²+ Ь — 1) — (62 — Ь + 1);

б) —12с ²+ 5с + (с + 118); г) (15 — 7у ²) — (у ^з— у ^а— 15).

590. Найдите сумму и разность многочленов:

591. Докажите, что:

а) сумма двух последовательных нечётных чисел кратна 4;

б) сумма четырёх последовательных нечётных чисел кратна 8.

592. Докажите, что выражение:

а) (х — у) + (у — 2) + (2 — х) тождественно равно О;

б) (а ²— 5ab) — (7 — ЗаЬ) + (2ab — а ²) тождественно равно —7.

131

593. Найдите многочлен, после подстановки которого вместо М следующее равенство окажется тождеством:

а) М + (5х ²— 2ху) = 6х ²+ 9ху — у ^ж, 6) М- (4аь - 36 ²) = - 7аЬ + 8b ²;

в) (48 - 78 + 6) - М = О.

594. Какой многочлен в сумме с многочленом 5х ²— 3х — 9 тождественно равен:

6) 18; г) х ²— 5х + 6?

595. Упростите выражение:

а) (0 ²- 0,450 + 1,2) + (0,80 ²- 1,20) - (1,60 ²- 20); 6) (у ²- 1,75у - 3,2) - (0,зу ²+ 4) - (2у - 7,2);

в) бху — 2х ²— (3ху + 4х ²+ 1) — (—ху — 2х ²— 1);

г) —(2ab ²— ab + Ь) + ЗаЬ ²— 46 — (5ab — ab ²).

596. Упростите выражение:

а) 8a ²b + (—5a ²b + 46 ²) + (a ²b — 5b ²+ 2);

б) (ху + х ²+ у ²) — (х ²+ у ²— 2ху) — ху.

597. Найдите значение выражения

(5,7а ²Ь - З,1аЬ + 88) - (6,9аЬ - 2,За ²Ь + 86 ³), если: а) а = 2 и Ь = 5; б) а = —2 и Ь = З.

598. Вычислите значение выражения 5х²— (3ху — 7х ²) + (5ху — 12х ²), если:

а) х = —0,25 и у = 4; б) х = —5 и у = 0,1.

599. Докажите, что при любом значении х разность многочленов 0,7х ⁴+ 0,2х ²— 5 и —0,3х ⁴+ —х ²— 8 принимает положительное

значение.

600. (Для работы в парах.) Учащимся была предложена задача:

«Найдите значение выражения

(70 ³- ба ²ь + 5аь ²) + (ба ^з+ 7а ²Ь + заь ²) - (10а ³+ a ²b + 8ab ²) при а = -0,25».

Один из учеников сказал, что в задаче не хватает данных. Прав ли он?

1) Обсудите друг с другом, в каком случае ученик окажется прав.

2) Выполните преобразования. З) Сделайте вывод.

601. Какой двучлен нужно сложить с многочленом .r ²+ у2 — 2ху + 1, чтобы в результате получился многочлен:

а) не содержащий переменную х;

б) не содержащий переменную у?

132	Глава lV

602. Докажите, что не зависит от х значение выражения

З 2

--х ²— 0,4ху — 1,5у + 1 у ^а— — ху + 0,6х ²

5 5

603. Докажите, что значение выражения не зависит от значения переменной:

а) - 106 ²- (1 - 36 ²) + (2,3 + 76 ²);

б) 1 — 62 _ (36 - 26 ²) + (1 + 36 - 6 ²).

604. Пусть х = 5а ²+ 6ab — b ²у = —4а ²+ 2ab + 36 ²= 9а ²+ 4ab. Подставьте эти многочлены вместо х, у и z в данное выражение и упростите его: а) х + у + г; б) х — у — 2.

605. Решите уравнение:

а) (23 + зх) + (8х - 41) = 15; 6) (19 + 2х) - (5х - 11) = 25;

в) (3,2у - 1,8) - (5,2у + 3,4) = -5,8;

г) 1 - (0,5х - 15,8) = 12,8 - 0,7х;

д) - 1,5у + (4,5у - 0,8) 2,4у + З;

е) 4,2у + = 6,2у - (1,1у + 0,8) + 1,2.

606. Решите уравнение:

а) 8у - 3 - (5 - 2у) = 4,3; 6) Обу - 1 -

в) —8х + (4 + 3х) = 10 — х;

г) 1,3х - 2 - (3,3х + 5) = 2х + 1.

607. Представьте выражение в виде суммы каких-нибудь двучленов: а) 3х ³— 2х ²— х + 4; б) —5у ⁴+ 4у ³+ Зу ²— 2у.

608. Представьте выражение каким-либо способом в виде разности одночлена и трёхчлена:

а) х ^з+ 2х ²— 3х — 5; б) За ⁴+ 2а ^з+ 5а ²— 4.

Известно, что при некоторых натуральных значениях п значение выражения п ^э+ п кратно 30, Будет ли кратно 30 при тех же значениях п значение выражения:

а) п ^э+ 31 п; б) п ^з— 29n?

610. (Для работы в парах.) Докажите, что сумма:

а) трёх последовательных натуральных чисел кратна З;

б) четырёх последовательных натуральных чисел не кратна 4. 1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

2) Проверьте друг у друга правильность выполнения преобразований.

З) Выскажите аналогичное предположение о сумме пяти последовательных натуральных чисел и проверьте, верно ли оно.

133

611. (ЗаДача-исслеДование.) В «Арифметике» Магницкого, написанной в начале XVIII в., предлагается такой способ угадывания задуманного двузначного числа: «Если кто задумал двузначное число, то скажи ему, чтобы он увеличил число десятков в 2 раза и к произведению прибавил 5 единиц; затем полученную сумму увеличил в 5 раз и к новому произведению прибавил 10 единиц и число единиц задуманного числа, а результат произведённых действий сообщил бы тебе. Если ты из указанного результата вычтешь 35, то узнаешь задуманное число» . 1) Выберите двузначное число и проверьте предложенный способ угадывания задуманного числа.

2) Предложите соседу по парте задумать двузначное число, выполнить указанные в условии задачи действия и сообщить результат.

З) Найдите число, задуманное соседом.

4) Докажите справедливость способа отгадывания задуманного двузначного числа, предложенного в учебнике Магницкого.

612. Представьте выражение в виде одночлена:

а) (2х2)3 . 2х24г) • (—4c ²d ²) ²;

6) -0,2а ²Ь ^З• (-5а ^ЗЬ ²) ²; д) (-pq)6 . (6P2q)3;

1 в) (—3у4)3 .е) (Зтп)⁴• (—3mn ²) ⁶.

С помощью калькулятора найдите значение выражения х ²У, если х = 1,4, у = 0,157.

Контрольные вопросы и задания

— 4ах • — х объясните, как при-

Дайте определение многочлена. На примере многочлена 5а ²х + ах

вести многочлен к стандартному Что называется степенью многочлена? члена третьей степени.

Составьте сумму и разность + Зу + 1 и преобразуйте каждое дартного вида.

В многочлене 5х ²— х + 4 заключите на, поставив перед скобками:

а) знак «плюс»; б) знак «минус».

виду.

Приведите пример много-

многочленов х ²— Зу + 6 и —х ²+ выражение в многочлен стан-

в скобки два последних чле-

134	Глава lV

— ОДНОЧЛЕНА

27. Умножение одночлена на многочлен

Умножим одночлен 9n ³на многочлен 7n ²— Зп + 4.

Для этого составим их произведение и преобразуем его, используя распределительное свойство умножения. Умножая одночлен на каждый член многочлена и складывая результаты, получим

9п ³(7п ²- зп + 4) =

= 9n ³• 7n ²— 9n ³• Зп + 9n ³• 4 = 63n ⁵— 27n ⁴+ Збп ^з

Произведение одночлена 9n ³и многочлена 7n ²— Зп + 4 мы представили в виде многочлена 63n ⁵— 27n ⁴+ Збп ^з

Вообще произведение одночлена и многочлена всегда можно представить в виде многочлена. При умножении одночлена на многочлен пользуются правилом:

Пример 1. Умножим одночлен —3а ²на многочлен 4а ³— а + 1.

Воспользуемся правилом умножения одночлена на многочлен:

—3а ²(4а ³— а + 1) = —3а ²• 40 ³— За ²• (—а) — За ²• 1 =

— —120 ⁵+ За ^з— За ²

Заметим, что запись можно вести короче, не выписывая промежуточные результаты:

—3а ²(4а ³— а + 1) = —12а ⁵+ За ^з— За ².

Пример 2. Упростим выражение 3х ²— 2х(х + 8).

» 3х ²- 2х(х + 8) = 3х ²- 2х ²- 16х = - 16х.

Умножение одночлена на многочлен часто применяется при решении уравнений.

Пример З. Решим уравнение 8 — 5х(х — 7) = 1 — 5х ²

Имеем

8 - 5х(х - 7) = 1 - 5х ²;

8 — 5х²+ 35х = 1 — 5х2;

—5х ²+ 35х + 5х ²= 1 — 8

35х = -7;

135

5 и

2х — 1 х + 5

Пример 4. Решим уравнение

9 6

Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 18:

2х — 1 х + 5

. 18 = 2 - 18•,

9 6

2х - 1

• 18 -• 18 = 36;

9 6

2(2х - 1) - + 5) = 36; - 2 - - 15 = 36;

614. Выполните умножение:

а) 2х(х ²- 7х - 3); г) (у ²— 2,4у + 6) • 1,5у; 6) -4b ²(5b ²- 36 - 2); д) -0,5х ²(-2х²- 3х + 4);

в) (За ^з— а ²+ а)(—5а ³); е) (—3у ²+ О,бу) (—1,5у ³).

615. Преобразуйте произведение в многочлен:

а) ЗаЬ (а ²— 2ab + 6 ²); г) (—2ах ²+ Зах — а ²) (—8х ²);

б) —х ²у (х ²у ²— .r ²— у ²); д) (6,3х ³у - зу ²-0,7х) • 10х ²у ²•,

в) — 2ab + 0,26 ²); е) — 1,5pq ²— 2q ³).

616. Представьте в виде многочлена:

617. Выполните умножение:

а) —3х ²(—х ^з+ х — 5);

в) — х ²у(15х — 0,9у + 6);

5 2 6

г) За ⁴х(а ²— 2ах + х ^з— 1);

д) (х ²у — ху + ху ²+ у ^з) • 3ху ²;

е) - оза + 35).

1 З а) — х (1,4х ²— 3,5у);Ь — —ab + —b

2 4

1 2 ²1

б) — бс); г) ——а ²у ⁵5ау

618. Упростите выражение и найдите его значение:

а) З(2х — 1) + 5(3 — х) при х = —1,5;

б) 25а — 4(За — 1) + 7 (5 — 2а) при а = 11;

в) 4у — 2(1Оу — 1) + (8у — 2) при у —- -0,1;

г) 12(2 — Зр) + 35р — 90 + 1) при р = 2.

619. Представьте в виде многочлена:

а) 146 + 1 - - 116); в) 14(7х - 1) - 7(14х + 1); 6) 25(2 - зс) + 16(5с - 1); г) 36(2 - у) - - И).

136

620. Упростите выражение:

а) 14у + 2у(6 — у); д) 7b(4c — Ь) + 4с(с — 7b);

б) Зу ²— 2у(5 + 2у); е) —2у(х ³— 2у) — (х ^зу + 4у ²);

в) 4х(х — 1) — 2 (2х ²— 1); ж) Зт ²(т + 5n) — 2n(8m ²— п);

г) 5а(а ²— За) — За(а ²— 5а); з) 6m ²n ³— п ²(6т ²п + п — 1).

621. Представьте в виде многочлена:

а) 6х(х — З) — х(2 — х); в) ах(2х — За) — х (ах + 5а ²);

б) —а ²(За — 5) + 4а (а ²— а); г) —4m ²(п ²— т ²) + Зп ²(т ²— п ²).

622. Найдите значение выражения:

а) —2х(х ²— х + З) + х (2х ²+ х — 5) при х = З; —3;

б) х (х — у) — у(у ²— х) при х = 4 и у = 2.

623. Вычислите значение выражения:

а) 5х(2х — 6) — 2,5х(4х — 2) при х = —8; 10;

б) 5а(а — 4b) — 4b(b — 5а) при а = —0,6 и Ь —0,5.

624. Упростите выражение:

а) (За ²) ²— а ^з(1 — 5а);

- ь 1- 2b -5 ²

в) х (16х — 2х3) — (2х2)2;

г) - 0,018 (48 - 100).

137

625. С помощью рисунка 67 разъясните геометрический смысл формулы а (Ь + с) = ab + ас для положитель- Рис. 67 ных значений а, Ь и с.

626. Докажите, что выражение х (2х + 1) — х ²при любом значении х принимает одно и то же значение.

627. Докажите, что значение выражения у(Зу ²— у + 5) — (2у ³+ Зу — 16) — у(у ²— у + 2) не зависит от у.

628. Докажите, что выражение тождественно равно нулю:

а) а (Ь — с) + b(c — а) + с (а — Ь);

б) а (Ь + с — bc) — b(c + а — ас) + с (Ь — а).

629. Докажите, что выражение 2х(х — 6) — З(х ²— 4х + 1) при любых значениях х принимает отрицательные значения.

630. Решите уравнение:

а) 5х+3(х— 1) = 6х+ 11; д) 6+(2 — 4х)+ 5= З(1 — 3х);

5 и

631. Найдите корень уравнения:

а) 3х(2х - 1) - 6х(7 + х) = 90; 6) + 2х) = зх(х + 1) - 30;

в) 5х(12х - 7) - 4х(15х - 11) = зо + 29х;

г) 24х — 6х(13х — 9) = -13 - 13х(6х - 1).

632. Решите уравнение:

а) 3(-2х + 1) - + 13) = 7х - - х);

б) —4(5 — 20) + З(а — 4) = 6(2 — а) — 5а;

в) Зу(4у — 1) — 2у(6у — 5) = 9у — 8(3 + у);

г) 15х + 6х(2 — 3х) = 9х(5 — 2х) — 36.

633. При каком значении переменной: а) значение выражения 2 (З — 5с) на 1 меньше значения выражения 4(1 — с);

б) значение выражения —3 (2х + 1) на 20 больше значения выражения 8х + 5;

в) значение выражения 5х + 7 в З раза меньше значения выражения 61 — 10х;

г) значение выражения 8 — у в 2 раза больше значения выражения 7 + у?

634. Решите уравнение:

4а 5а

14 г) 2z +3= — ж)

4з12'

а а 6)

635. Найдите корень уравнения:

636. Решите уравнение:

а)

б)

637. Найдите корень уравнения:

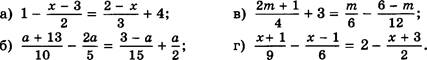
	Глава lV

638. Решите уравнение: бу + 7 8 — 5у

а) 4 З ба - 1 2а - З 6) - 1; з 5

11х — 4 х —9

в)

7 2

г) 9 4 6 зр - 1

д)- 1 = 0; 24 36

1- 2х 3х + 20 х

4 6

639. Периметр треугольника 44 см. Одна из его сторон на 4 см меньше другой и в 2 раза больше третьей стороны. Найдите стороны треугольника.

640. Фирма арендует три помещения общей площадью 166 м ². Площадь одного из них в полтора раза больше площади другого и на 6 м ²меньше площади третьего. Найдите площадь каждого помещения.

641. Старинная задача. Трое выиграли некоторую сумму денег. На

1 1

долю первого пришлась — этой суммы, на долю второго а на долю третьего — 17 флоринов. Как велик весь выигрыш?

642. В первом сарае было сложено сена в З раза больше, чем во втором. После того как из первого сарая взяли 2 т, а во второй добавили 2 т сена, во втором сарае оказалось — того, что осталось в первом сарае. Сколько тонн сена было в каждом сарае?

643. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на один день быстрее, чем планировалось. Какова площадь луга?

644. Увеличив среднюю скорость с 250 до ЗОО м/мин, спортсменка стала пробегать дистанцию на 1 мин быстрее. Какова длина дистанции?

645. От турбазы до привала туристы шли со скоростью 4,5 км/ч, а возвращались на турбазу со скоростью 4 км/ч, затратив на обратный путь на 15 мин больше. На каком расстоянии от турбазы был сделан привал?

646. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В, отстоящего от пункта А на расстоянии 60 км, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/ч, а мотоциклист — со скоростью 30 км/ч. На каком расстоянии от пункта А мотоциклист догонит велосипедиста?

647. Из пункта А вышла грузовая машина со скоростью 60 км/ч. Через 2 ч вслед за ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?

648. В 190 г водного раствора соли добавили 10 г соли. В результате концентрация раствора повысилась на 4,5 ⁰/0 . Сколько соли было в растворе первоначально?

649. В сплав олова и меди массой 16 кг добавили 2 кг олова. После этого содержание олова в сплаве повысилось на 5 ⁰/0 . Сколько олова было в сплаве первоначально?

650. Найдите координаты точки пересечения графиков линейных функций:

а) у 5х + 29 и у = —3х б) у = 1,2х и у = 1,8х + 9,3. 651. В каких координатных четвертях расположен график функции:

а) у = -28х; в) у = 0,05х;

6) у- -28х + 4; г) у = 0,05х — 2,5?

652. Решите графически уравнение х ²= 6 — х.

653. Упростите выражение:

1 а) —а5у3 • (—ау)³, б) —0, 1a ⁴b ⁷• (—30a ²b) ². з

28. Вынесение общего множителя за скобки

При решении уравнений, в вычислениях и ряде других задач бывает полезно заменить многочлен произведением нескольких многочленов (среди которых могут быть и одночлены). Представление многочлена в виде произведения двух или нескольких многочленов называют разложением многочлена на множители.

Рассмотрим многочлен 6a ²b + 15b ². Каждый его член можно заменить произведением двух множителей, один из которых равен 3b:

ба ²Ь + 15b ²= • 2а ²+ 36 • 5b.

Полученное выражение на основе распределительного свойства умножения можно представить в виде произведения двух множителей. Один из них — общий множитель 36, а другой — сумма 2а ²и 5b: 36 • 2а ²+ ЗЬ • 5b = ЗЬ(2а ²+ 5b).

Итак, ба ²ь + 156 ²= 3b(2a ²+ 56).

Мы разложили многочлен на множители, представив его в виде произведения одночлена 3b и многочлена 2а ²+ 5b. Применённый способ разложения многочлена на множители называют вынесением общего множителя за скобки.

140	Глава

Рассмотрим примеры разложения многочлена на множители с помощью вынесения общего множителя за скобки.

Пример 1. Разложим на множители многочлен —15х ²у ³— 30х ³у ²+ 45х ⁴у.

Члены этого многочлена имеют различные общие множители: х, у, 3ху, —5х ²и др. Обычно в многочлене с целыми коэффициентами множитель, выносимый за скобки, выбирают так, чтобы члены многочлена, оставшегося в скобках, не содержали общего буквенного множителя, а модули их коэффициентов не имели общих натуральных делителей, кроме 1.

В многочлене —15х ²у^З— 30х ³у ²+ 45х⁴у модули коэффициентов числа 15, 30 и 45. Их наибольший общий делитель равен 15. Поэтому в качестве коэффициента общего множителя можно взять число 15 или —15. Все члены многочлена содержат переменные х и у. Переменная х входит в них во второй, третьей и четвёртой степенях, поэтому за скобки можно вынести х ². Переменная у содержится в членах многочлена в третьей, второй и первой степенях, поэтому за скобки можно вынести у. Итак, за скобки целесообразно вынести одночлен 15х ²у или —15х ²у. Вынесем, например, за скобки —15х ²у. Получим

—15х ²у ³— 30х ³у ²+ 45х ⁴у = —15х ²у(у ²+ 2ху — 3х ²). <

Пример 2. Разложим на множители выражение 3a ²(b - 2с) + - 2с).

В этой сумме каждое слагаемое содержит множитель Ь — 2с. Вынесем этот множитель за скобки:

3a ²(b - 2с) + - 2с) = Ф - + 7). <

Пример З. Представим в виде произведения сумму

Множители х — у и у — х отличаются друг от друга лишь знаком. Вынесем в выражении у — х за скобки —1, получим

а (х — у) + b(y — х) = а (х — у) + b(—1)(x — у) = = а (х — у) — b(x — у) = (х — у)(а — Ь).

Запись можно вести короче:

— а (х — у) — b(x — у) = (х — у)(а — Ь). <

Заметим, что преобразование Ь (у — х) = —b (х — у) можно объяснить иначе: если изменить знак у второго множителя и перед произведением, то значение выражения не изменится.

141

Пример 4. Решим уравнение 2х ²+ 3х = О.

В выражении 2х ²+ 3х вынесем за скобки множитель х. Получим х(2х + 3) = о.

Произведение х (2х + З) равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, т. е. когда

х = О или 2х + З = О.

Решая уравнение 2х + З = О, находим 2х = —3, х = —1,5.

Следовательно, произведение х (2х + З) обращается в нуль при х = О и при х = —1,5, т. е. уравнение 2х ²+ 3х = О имеет два корня: О и —1,5.

Запись можно вести короче:

2х ²+ 3х о, х(2х + 3) = о, х = О или 2х + З = О, х = О или х = —1,5. Ответ: О и —1,5.

Пример 5. Докажем, что сумма 3 ⁹+ 3 ⁷+ 3 ⁶делится на 31.

Вынесем в выражении 3 ⁹+ 3 ⁷+ 3 ⁶за скобки 3 ⁶:

3 ⁹+ 3 ⁷+ 3 ⁶= 3 ⁶(3 ³+ 3 + 1) = 3 ⁶(27 + 3 + 1) = 3 ⁶• 31.

Мы представили сумму 3 ⁹+ 3 ⁷+ 3 ⁶в виде произведения двух целых чисел, одно из которых равно 31. Значит, данная сумма делится на 31.

654. Разложите на множители и сделайте проверку:

а) тх + ту; б) Кх — рх; в) —ab + ас; г) —та — па.

655. Вынесите за скобки общий множитель:

а) 5х + 5у; г) —6m — 9n; ж) ab + а;

б) 4а — 4b; д) ах + ау; з) су с

в) Зс + 15d; е) bc — bd; и) —та — а.

656. Представьте в виде произведения:

в) 12х + 48у; д) 12а + 12;

г) —9m — 27 п; е) -10 - 10с.

657. Разложите на множители: а) 7ах + 7bx; д) 5у ²— 15у; 6) зьу - 6b; е) 3х + 6х ²; в) —5mn + 5n; ж) а ²— ab; Г) За + 9ab; з) 8mn — 4m ²;		и) —6ab + 9b ²; к) х ²у — ху ², л) ab — a ²b; м) -p²q ²- pq.
142	Глава lV

658. Вынесите за скобки общий множитель:

ж) 48 —

д) Зт ²+ 9m ³; з) 5х ⁵— 15х ³;

е) 9р ³— 8р; и) —12у⁴— 16у.

659.	Представьте в виде произведения:
	а) 14х+ 21 у; г) 9ха + 9xb; ж) т ⁴— т ²,	к) 16у³+ 12у ²;
	6) 150 + 10b; д) баб— За; з) с ³+с ⁴,	л) 18ab ³— 96⁴;
	в) 8ab — бас; е) 4х— 12х²; и) 7х— 14х ³;	м) 4х ³у²— 6х ²у ³.

660. Найдите значение выражения:

а) 3,28х — х ²при х = 2,28;

б) а ²у + а ^зпри а = —1,5 и у = —8,5;

в) ау²— у ^зпри а = и у —1,2;

г) —mb — при т = 3,48 и Ь = 96,52.

661.	Решите уравнение:
	а) х ²+ 8х = О; г) 3х ²- 1,2х = о;	ж) х — 10х ²= О;
	б) 5х ²— х = О; д) 6х ²— 0,5х = О; в) бу? — ЗОУ = О;	з) 6х — 0,2х ²= О;
662.	Найдите корни уравнения:
	а) 5х ²+ 3х = О; в) 6х ²— 3,6х = О;	д) 5х ²— 0,8х = О;
	6) х ²- 11х = о; г) 0,3х ²- 3х = о;	е) 7х ²- 0,28х = О.

663. (Для работы в парах.) Докажите, что значение выражения:

а) 16 ⁵+ 16 ⁴кратно 17; в) 36 ⁵— 6 ⁹кратно 30;

б) 38 ⁹— 38⁸кратно 37; г) 5 ¹⁸— 25 ⁸кратно 120.

1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их.

2) Проверьте друг у друга правильность выполнения заданий. З) Предложите друг другу составить задание, аналогичное заданию б).

664. Разложите на множители:

а) х ⁵+Х ⁴— х ^з, в) а ⁴+а ⁵— а ⁸,

г) —b10 _ Ь 15 _ b20

665. (Для работы в парах.) Докажите, что:

а) 7 ⁸— 7 ⁷+ 7 ⁶делится на 43;

б) 2 ¹³— 2 ¹⁰— 2 ⁹делится на 13;

в) 27 ⁴— 9 ⁵+ 3 ⁹делится на 25;

г) 16 ⁴— 2 ¹³— 4 ⁵делится на 110.

1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их.

2) Проверьте друг у друга правильность выполнения заданий и исправьте ошибки, если они допущены.

З) Обсудите, какие свойства делимости использованы при выполнении задания.

143

666. Разложите на множители многочлен: а) х ³— 3х ²+ х; в) 4а ⁵— 2а ³+а;

б) т ²— 2m ³— т ⁴; г) 6х ²— 4х ³+ 10х ⁴; 667. Представьте в виде произведения:

д) 15а ³— 9а ²+ ба;

е) —3m ²—6m ³+ 12m ⁵

а) с ^з— с ^а+ 2с ⁵; в) 4х ⁴+ 8х³— 2х ²;

б) 5m ⁴— т ^з+ 2m ²; г) 5а — 5а ²— 10а ⁴

668. Вынесите за скобки общий множитель:

а) За ^з— 15a ²b + 5ab ²; г) 12a ²b — 18ab ²— 30ab ³;

б) 20х⁴— 25х ²у ²— 10х3; д) 4ах ³+ 8а ²х²— 12а ³х;

в) —6ат ²+ 9m ³— 12m ⁴; е) —3х⁴у ²— 6х ²у ²+ 9х ²у ⁴.

669. Разложите на множители многочлен:

а) 4с ⁴— 6х ²с ²+ 8с; в) Зах — бах ²— 9а ²х;

б) 10а ²х — 15а ³— 20а ⁴х; г) 8a ⁴b ³— 12a ²b⁴+ 16a ³b ²

670. Укажите общий множитель для всех слагаемых суммы и вынесите его за скобки:

а) 2а(Х + у) + ь (х + у); г) 9ф — 1) + ф — 1) ²;

е) -3b(b - 2) + - 2) ².

144

671. Представьте выражение в виде произведения двух многочленов:

а) а (Ь — с) + d(c — Ь);

б) х(у — 5) — у (5 — у);

в) За(2х - 7) + 5b(7 - 2х);

672. Разложите на множители:

а) 8т(а — З) + п (а — З); г)

6) (р2 - 5) - q(p2 - 5); д)

е) —(х + 2у) — 4(х + 2у) ².

673. Велосипедист проехал путь АВ со скоростью 12 км/ч. Возвращаясь из В в А, он развил скорость 18 км/ч и затратил на обратный путь на 15 мин меньше, чем на путь из А в В. Сколько километров между А и В?

674. Решите уравнение:

3х - 5 8х - 12 21- 4х 8х + 15

а) 6)

2 7 9 з

675. Известно, что значение выражения а — Ь при некоторых значениях а и Ь равно 0,5. Чему равно при тех же а и Ь значение выражения:

в) (а — Ь) ²; г) (Ь — ау; д) (а — Ь) ³; е) (Ь — а) ³?

676. Запишите в виде выражения:

а) произведение разности а и Ь и их суммы;

б) сумму квадратов а и Ь;

в) квадрат суммы а и Ь;

г) разность квадратов Ь и с;

д) куб разности Ь и с;

е) сумму кубов Ь и с.

Контрольные вопросы и задания

одночлена на многочлен.

Сформулируйте правило умножения Преобразуйте в многочлен и х ²+ ХУ + у ²

Какое преобразование называют множители?

На примере многочлена 2ху — 6х разложение на множители скобки.

произведение ab и а + 46; ху

разложением многочлена на

²объясните, как выполняется вынесением общего множителя за

МНОГОЧЛЕНОВ

29. Умножение многочлена на многочлен

Умножим многочлен а + Ь на многочлен с + d. Составим произведение этих многочленов:

(а + Ь)(с + d).

Обозначим двучлен а + Ь буквой х и преобразуем полученное произведение по правилу умножения одночлена на многочлен: (а + + d) = х (с + d) = хс + xd.

В выражение хс + xd подставим вместо х многочлен а + Ь и снова воспользуемся правилом умножения одночлена на многочлен: хс + ха? = (а + Ь)с + (а + b)d = ас + bc + ad + bd.

Итак,

(а + Ь)(с + d) = ас + bc + ad + bd.

Произведение многочленов а + Ь и с + d мы представили в виде многочлена ас + bc + ad + bd. Этот многочлен является суммой всех одночленов, получающихся при умножении каждого члена многочлена а + Ь на каждый член многочлена с + d.

145

При умножении многочлена на многочлен пользуются правилом:

чтобы умножить многочлен йа Авогочле*, ну=Ь

I член одного многочлена умножить на каж№й члеЁ др*ого многочлена и полученные произведени; ёЛ6жит'.

Заметим, что при умножении многочлена, содержащего т членов, на многочлен, содержащий п членов, в произведении (до приведения подобных членов) должно получиться тп членов. Этим можно пользоваться для контроля.

В древности справедливость некоторых равенств при положительных значеРис. 68 ниях переменных математики доказывали геометрически. Так, великий греческий математик Евклид в своём трактате «Начала» (Ш в. до н. э.) справедливость равенства (а + Ь) (с + d) = ас + Ьс + ad + bd доказывал с помощью чертежа, изображённого на рисунке 68.

При мер 1. Умножим многочлен 4х ²+ 2ху — у ²на многочлен 2х — у.

Имеем

(4х ²+ 2ху — у ²)(2х — у) =

= 8х ³+ 4х ²у — 2ху ²— 4х ²у — 2ху ²+ у ^з= 8х ³— 4ху ²+ у ^з.

Пример 2. Упростим выражение (2а — 3)(5 — а) — За (4 — а).

Имеем

(2а — 3)(5 — а) — За (4 — а) = Ша — 15 — 2а ²+ За — (12а — За ²) = = 130 - 15 - 20 ²- 120 + = + а - 15.

Пример З. Докажем, что при любом натуральном п значение выражения п (п — 5) — (п — 14)(n + 2) кратно 7. Выполним преобразование:

п (п — 5) — (п — 14)(n + 2) = п ²— 5n — (п ²— 14n + 2n — 28) = - 5п - + 14п - + 28 = + 28 = + 4).

При любом натуральном п произведение 7 (п + 4) делится на 7, а значит, и значение выражения п (п — 5) — (п — 14)(n + 2) делится на 7.

146	Глава lV

Пример 4. Докажем, что равенство

(а + Ь) (а ^з— a ²b + ab ²— Ы) = (а — + a ²b + ab ²+ Ы)

является тождеством, или, как говорят иначе, докажем тождество.

Преобразуем обе части равенства:

a2b + ab2 — Ы) = а4 — a3b + a2b2 _ ab ³+ a ³b — a ²b ²+ + ab3 _ b4 —— а ⁴b ⁴

(а — + a ²b + ab ²+ Н) = а ⁴+ a ³b + a ²b ²+ ab ³— a ³b — a ²b ²— — ab ³— b⁴= а ⁴— b⁴

Так как левая и правая части равенства тождественно равны одному и тому же выражению, то они тождественно равны между собой. Значит, исходное равенство — тождество.

Иногда, для того чтобы доказать тождество, преобразуют левую часть равенства в правую или правую в левую.

677. Выполните умножение:

а) (х + т)(у + п);д)

г) (х + 8)(у — 1)е)

678. Упростите выражение:

а) (х + б)(х + 5);д)

б) (а — 4)(а + 1);

679. Представьте в виде многочлена выражение:

а) (т — п)(х + с); в) (а + З)(а — 2); д)

б) (К — p)(k — п); г) (5 — х)(4 — х); е) (бт —3) (2 — 5m).

680. Запишите в виде многочлена выражение:

а) (х ²+ у)(х + у ²); г) (5х ²— 4х)(х + 1);

б) (т ²— + 2,0 ²); д) (а — 2)(4а ³— За ²);

в) (4а ²+ — b ²); е) (7р ²— 2р)(8р — 5).

681.	Выполните умножение:
	а) (2х ²— у)(х ²+ у);	в) (11у ²— 9)(Зу — 2);
	б) (7х ²+ — За ²);	г) (5а — За ³)(4а — 1).

682. Замените степень произведением, а затем произведение преобразуйте в многочлен:

а) (х + 10) ²;г) (5 — 6b) ².

683. Представьте в виде многочлена выражение:

а) (х? + ху — + у); д) (а ²— 2а + З)(а — 4);

б) (п ²— пр + — р); е) (5х — — х — 1);

в) (а + х)(а ²— ах — х ²); ж)

г) (Ь — — bc — 8); з) (Зу — — у + 1).

5 1

147

684. Запишите в виде многочлена:

а) (с2 — cd — + d); в) (40 ²

б) (х — у)(х ²— ху — у ²);

685. Представьте в виде многочлена:

а) у ²(у + 5)(у — З);

б) 2а ²(а — 1)(3 — а);

686. Запишите в виде многочлена выражение:

б) (а — 1)(а — 4)(а + 5).

687. Упростите выражение:

6) (7у - + 3) - 13у•,

в) х ^з— (х ²— Зх)(х + З);

г) 5b ³+ (а ²+ 5b)(ab — b ²);

е) (х + у)(х — у) — (х — 1)(х — 2).

688. Значения каких переменных надо знать, чтобы найти значение выражения (За — 2b)(2a — 3b) — ба (а — Ь) + 7ab? Выберите верный ответ.

1. Переменных а и Ь

2. Только переменной а

З. Только переменной Ь

4. Ни одной из переменных а и Ь, так как значение выражения не зависит от значений переменных

689. Зная, что а = 3х — 1, Ь = х + 1, с = 2х + 4, d = 6х — 5, представьте в виде многочлена с переменной х выражение ас — bd.

690. Докажите, что при любом значении х:

а) значение выражения (х — З) (х + 7) — (х + 5) (х — 1) равно —16;

б) значение выражения х ⁴— (х ²— 7) (х ²+ 7) равно 49.

691. Докажите тождество:

а) (с — 8)(с + З) = с ²— 5с

б) + зт — 28 = (т — 4)(m + 7).

692. Докажите тождество:

а) (х - + 7) - 13 = (х + - 4) - 2; 6) 16 - (а + + + - 1).

693. Докажите, что значение выражения не зависит от переменной х:

а) (х — 5)(х + 8) — (х + 4)(х — 1); б) х^а— (х ²— + 1).

694. Докажите, что выражение (у — 6) (у + 8) — 2 (у — 25) при любом значении у принимает положительное значение.

695. Докажите, что при всех целых п значение выражения:

а) п (п — 1) — (п + З)(п + 2) делится на 6;

б) п (п + 2) — (п — 7)(n — 5) делится на 7.

148	Глава lV

696. Пусть а, Ь, с и d — четыре последовательных нечётных числа. Докажите, что разность cd — ab кратна 16. 697. Решите уравнение:

а) (3х - + 4) - 15х ²= 17;

в) 12 - - 3) = (6 - + 2);

г) (х + 4)(х + 1) = х — (х — 2)(2 — х).

698. Найдите корень уравнения:

г) х ²+ х (6 — 2х) = (х — 1)(2 — х) — 2.

699. Докажите, что:

а) при любом натуральном значении п значение выражения п (п + 5) — (п — З)(п + 2) кратно 6;

б) при любом натуральном значении п, большем 2, значение выражения (п — 1)(n + 1) — (п — 7)(п — 5) кратно 12,

700. Найдите три последовательных натуральных числа, если известно, что квадрат меньшего из них на 65 меньше произведения двух остальных.

701. Три последовательных нечётных числа таковы, что если из произведения двух ббльших чисел вычесть произведение двух меньших, то получится 76. Найдите эти числа.

702. Периметр прямоугольника равен 70 см. Если его длину уменьшить на 5 см, а ширину увеличить на 5 см, то площадь увеличится на 50 см ². Найдите длину и ширину первоначального прямоугольника.

703. Сторона квадрата на З см меньше одной из сторон прямоугольника и на 2 см больше другой его стороны. Найдите сторону квадрата, если известно, что площадь квадрата на 30 см ²меньше площади прямоугольника.

704. Для выполнения планового задания к определённому сроку бригада рабочих должна была изготовлять ежедневно 54 детали. Перевыполняя план на 6 деталей в день, бригада уже за один день до срока не только выполнила плановое задание, но и изготовила 18 деталей сверх плана. Сколько дней работала бригада?

705. Тракторная бригада должна была по плану вспахивать ежедневно 112 га. Перевыполняя план на 8 га в день, бригада уже за день до срока закончила пахоту. Сколько гектаров нужно было вспахать бригаде?

149

706. Решите уравнение:

2х - 5

а)б)

5 6 4 з 707. Прочитайте выражение:

а) а2 + b2; б) (а + Ь) ²; 3

30. Разложение многочлена на множители способом группировки

Мы познакомились с разложением многочлена на множители способом вынесения общего множителя за скобки. Иногда удаётся разложить многочлен на множители, используя другой способ — группировку его членов.

Пример 1. Разложим на множители многочлен ab — 26 + За — 6. Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель:

аЬ - 2b + За (аь - 2b) + (За - 6).

В первой группе вынесем за скобки множитель Ь, а во второй множитель З:

Каждое слагаемое получившегося выражения имеет множитель а — 2. Вынесем этот общий множитель за скобки:

Итак, аЬ - 2b + За - 6 = (а - + 3).

Разложение многочлена ab — 26 + За — 6 на множители можно выполнить, группируя его члены иначе:

- 26 + За - 6 = (аь + за) + (-26 - 6) =

Пример 2. Разложим на множители многочлен ас + bd — bc — ad. Сгруппируем первый член многочлена с третьим и второй с четвёртым. В первой группе вынесем за скобки множитель с, а во второй — множитель —d. Получим ас + bd — bc — ad = (ас — bc) + (bd — ad) =

150	Глава lV

Пример З. Разложим на множители трёхчлен а ²— 7а + 12.

- Представим —7а в виде —3а — 4а и выполним группировку:

- 70 + 12 = - за - + 12 = - за) + (-40 + 12) =

Способ, который мы применили в примерах 1—3 для разложения многочленов на множители, называют способом группировки.

708. Представьте в виде произведения многочленов выражение:

в) р(с — d) + c — d;

б) у (а — с) + 5а — 5с;

709. Разложите на множители многочлен:

а) тх + ту + 6х + бу; г) ах + ау — х — у;

д) 1 — bx — х + Ь;

в) 7а — 76 + ап — Ьп; е) ху + 2у — 2х — 4.

710. Разложите на множители многочлен:

а) ab — 8а — bx + 8х; в) ах — у + х — ау;

б) ах — Ь + bx — а; г) ах — 2bx + ау — 2by.

711. Разложите на множители многочлен:

б) у ⁵— у ^з— у ²+ 1;

в) а⁴+ 2а ³— а — 2;

г) b ⁶— 3b ⁴— 2b ²+ 6;

д) а ²— ab — 8а + 8b;

е) ab — 3b + b ²— За;

ж) 11х — ху + 11 у — х ²,

з) Кп — тп — п ²+ тк.

712. Представьте в виде произведения многочлен:

а) тп — тк + хк — хп; в) зт — тк + ЗК — Р;

б) х ²+ 7х — ах — 7а; г) хк — ху — х ²+ УК.

713. Найдите значение выражения:

а) p ²q ²+ pq — q ³— Р ^Зпри р = 0,5 и —0,5;

2 1

б) 3х ³— 2у ³— 6х ²у ²+ ху при х = — и у= — з 714. Чему равно значение выражения: а) 2а + ас ²— а ²с — 2с при а = 1— и с = —1 ^Ц; з

б) х ²у — у + ху ²— х при х = 4 и у = 0,25?

715. Докажите тождество:

а) ах — у + х — ау = (х — у)(а + 1);

б) ах — 2by + ау — 2bx = (а — 2b)(x + у).

151

716. Представьте в виде произведения:

а) ас ²— ad + с ^з— cd — bc ²+ bd;

б) ах ²+ ау ²— 6х ²— by ²+ Ь — а;

в) ап ²+ сп ²— ар + ар ²— ср + ср ²,

г) ху ²— by ²— ах + ab + у ²— а.

717. Разложите на множители многочлен:

а) х ²у + х + ху ²+ у + 2ху + 2; б) х ²— ху + х — ху ²+ у

718. Разложите на множители трёхчлен:

а) х ²+ 6х + 5; б) х ²— х — 6; в) а ²— 5а + 4; г) а ²— ба — 16.

719. Число коров в стаде возросло на 60 голов, а в связи с улучшением кормовой базы удой молока от одной коровы возрос в среднем с 12,8 л в день до 15 л. Сколько коров стало в стаде, если ежедневно стали получать на 1340 л молока больше, чем раньше? 720. Решите уравнение:

а) 4 — х (х + 8) = 11 — х ², 6) 4х(3х - 1) - 2х(6х + 8) = 5.

721. Запишите в виде выражения:

а) квадрат разности х и у;

б) сумму числа З и произведения а и Ь;

в) разность числа 7 и удвоенного произведения а и Ь.

Контрольные вопросы и задания

многочлена на многочлен. произведение многочленов

Сформулируйте правило умножения Представьте в виде многочлена х — 29' и ху + 4.

На примере многочлена ab — 2b + ется разложение многочлена на

5а — 10 объясните, как выполнямножители способом группировки.

Для тех, кто хочет знать больше

31 . Деление с остатком

Вам неоднократно приходилось встречаться со случаями, когда при делении одного натурального числа на другое получается остаток. Например, при делении числа 143 на 7 в частном получается 20 и в остатке З:

143 : 20 (ост. 3),

причём остаток З меньше делителя.

152	Глава IV

Если из 143 вычесть З, то полученная разность будет делиться на 7:

143 - 3 = 7 . 20.

В том случае, когда одно натуральное число делится на другое без остатка, условились считать, что остаток равен нулю.

Вообще число r называется остатком от деления натурального числа а на натуральное число Ь, если выполняются два условия: а — r делится на Ь и О r< Ь.

Определение остатка, принятое для натуральных чисел, переносится на случай, когда делимое является целым числом, а делитель — натуральным числом.

Целое число r называют остатком от деления целого числа а на натуральное число Ь, если разность а — r делится на Ь и Ь.

Обозначив частное от деления а — r на Ь буквой q, получим, что а — bq.

Отсюда а = bq + r, где О Ь.

Например:

—13 = 5 • (—3) + 2, причём (К 2 < 5.

Частное от деления числа —13 на 5 равно —3, а остаток равен 2. При решении задач широкое применение находит следующее утверждение:

Для любого целого числа а и натурального Ь существует единственная пара целых чисел q и r, таких, что а = bq + r, где О r < Ь.

В справедливости этого утверждения можно убедиться, обратившись к координатной прямой. Пусть на координатной прямой ОТМечены числа, кратные Ь (рис. 69). Они разбивают координатную прямую на отрезки, концами которых являются точки с координатами bq и b(q + 1), где q — целое число. Длина каждого из этих отрезков равна Ь. Произвольное число а изображается точкой, которая либо совпадает с левым концом отрезка, ограниченного точками с координатами bq и b(q + 1), либо находится внутри этого отрезка. В первом случае а = bq, т. е. а = bq + О, а во втором а = bq + r, где О r < Ь. Таким образом, в любом случае найдётся единственная пара целых чисел q и r, такая, что а = bq + r, где О r < Ь.

Рис. 69

153

Для тех, кто хочет знать больше

На делении с остатком основаны различные разбиения множества целых чисел на классы, т. е. на подмножества, не имеющие общих элементов.

Например, при делении числа на З могут получиться остатки О, 1 и 2. Соответственно множество целых чисел можно разбить на три класса:

множество чисел вида ЗК, множество чисел вида ЗК + 1, множество чисел вида ЗК + 2, где К — целое число.

Аналогично, исходя из остатков от деления целого числа на 5, множество целых чисел можно разбить на пять классов: множество чисел вида 5k, множество чисел вида 5k + 1, множество чисел вида 5k + 2, множество чисел вида 5k + З, множество чисел вида 5k + 4, где К — целое число.

Пример. Докажем, что если целые числа а и Ь дают при делении на З одинаковые остатки, не равные нулю, то число аЬ — 1 делится на З.

По условию числа а и Ь дают при делении на З одинаковые остатки, не равные нулю. Значит, либо а = ЗК + 1 и Ь = Зр + 1, либо а = ЗЁ + 2 и Ь = Зр + 2, где К ир — целые числа. В первом из этих случаев имеем

Во втором случае имеем

ab — 1 — 1 = 9Кр + + 6k + 4 — 1 = бК З = З (ЗКр + + 2k + 1).

Таким образом, в каждом из рассмотренных случаев число ab — 1 делится на З.

Найдите частное и остаток от деления:

а) 138 на 7; б) —16 на З; в) —4 на 5.

Найдите наибольшее целое отрицательное число, которое при делении на 11 даёт остаток 1.

Укажите все целые числа а, удовлетворяющие двойному неравенству —12 < а < 12, которые при делении на 7 дают остаток З.

154	Глава lV

Укажите наибольшее число воскресений в году.

При делении целого числа т на 35 в остатке получили 15. Делится ли число т на 5? на 7?

При делении натурального числа а на натуральное число Ь в частном получили с и в остатке d. Могут ли все числа а, Ь, с и d быть нечётными?

Докажите, что если целые числа а и Ь при делении на З дают различные остатки (отличные от нуля), то число ab + 1 делится на З.

Верно ли, что при любых целых значениях а и Ь произведение ab(a + — Ь) делится на З?

При делении целого числа а на 12 получается остаток 5. Какой остаток получится при делении этого числа на 4?

Одно из двух целых чисел при делении на 9 даёт остаток 7, а другое даёт остаток 5. Какой остаток получится при делении на 9 их произведения?

Найдите целое число, которое как при делении на 5, так и при делении на 7 даёт остаток 1, причём первое частное на 4 больше второго.

Докажите, что произведение п (2п + 1)(7n + 1) делится на 6 при любом натуральном п.

к главе lV

К параграфу 9

Найдутся ли такие целые значения х, при которых значение многочлена:

а) 2х²+ 6х + З окажется чётным числом;

б) х ²+ х + 2 окажется нечётным числом?

735. Расположите члены многочлена Зах ²— ба ^зх + 8а ²— хз.

а) по возрастающим степеням переменной х;

б) по убывающим степеням переменной а.

736. Представьте в виде многочлена:

а) (—2х ²+ Х + 1) — (Х ²— Х -4- 7) — (4х ²+ 2х + 8); 6) (30 ²- а + 2) + (-30 ²+ За - 1) - - 1);

в) 20 — 3b + с — (40 + 7Ь + с + З);

г) 2ху — у ²+ (у ²— ху) — (х ²+ ху).

737. Упростите выражение:

а) (1 — х + 4х ²— 8х ³) + (2х ³+ х ²— 6х — З) — (5х ³+ 8х ²); 6) (0,5а - 0,6b + 5,5) - (-0,50 + 0,4b) + (1,ЗЬ - 4,5).

155

738. Докажите, что выражение А + В — С тождественно равно выражению С — В — А, если А = 2х — 1, В = 3х + 1 и С = 5х.

739. Какой многочлен нужно вычесть из многочлена у чтобы разность была тождественно равна:

г) 4у ²— у + 7?

740. Докажите, что при любом значении х разность многочленов

1 0,4х -!

1 х ⁴- -х^з- 1-х ²+ -х+- и 0,75х⁴- 0,125х³- 2,25х ²+

8 7

принимает положительное значение.

741. Докажите, что при любом значении а сумма многочленов

,4а ³— а ²5

5 5

принимает отрицательное значение.

742. Запись abc означает число, в котором а сотен, Ь десятков и с единиц. Это число можно представить в виде многочлена

abc = 100а + 10b + с.

Например, 845 = 100 • 8 + 10 • 4 + 5. Представьте в виде многочлена число:

а) ху; б) ух; в) аОЬ; г) abcd.

743. Представьте в виде многочлена и упростите получившуюся сумму или разность:

а) abc + cba; б) abc + bc; в) abc — ba; г) abc — ас.

Докажите, что:

а) сумма чисел ab и ba кратна сумме а и Ь;

б) разность чисел ab и ба кратна 9.

745. Решите уравнение:

6) 5 - Зу - (4 - 2у) = у - 8 - (у - 1);

1 в) 7 — 1—а + — а — 5— = 2а 2

г) —3,6 — (1,5х + 1) = -4х - - (0,4х - 2).

746. Найдите четыре числа, пропорциональные числам 2, 4, 5 и 6, если разность между суммой двух последних и суммой двух первых чисел равна 4,8.

Если к задуманному числу приписать справа нуль и результат вычесть из числа 143, то получится утроенное задуманное число. Какое число было задумано?

156	Глава lV

Если к данному числу приписать справа цифру 9 и к полученному числу прибавить удвоенное данное число, то сумма будет равна 633. Найдите данное число.

К трёхзначному числу слева приписали цифру 5 и из полученного четырёхзначного числа вычли 3032. Получилась разность, которая больше трёхзначного числа в 9 раз. Найдите это трёхзначное число.

Трёхзначное число оканчивается цифрой 7. Если эту цифру переставить на первое место, то число увеличится на 324. Найдите это трёхзначное число.

К параграфу 10

751. Преобразуйте произведение в многочлен:

а) (х⁴+ 7х ²у ²— 5у ⁴) (—0,2ху ²);

1 2

_ _b5c + —ЬЗсЗ - -с ⁵(-3068);

2 5

1 в) —a ⁵b — ab + — (-21862);

1 г) (0,5х ⁷у ¹²— бху — 1) —— ху 6 752. Упростите выражение:

а) 5(4х ²- 2х + 1) - 2(10х ²- 6х - 1); 6) 7(2у ²- - 3) - 4(3у ²- 9у - 5);

в) a(3b - 1) - - 3) - 2(аь - а + Ь);

г) х ²(4 — у ²) + у ²(х ²— 7) — 4х(х — З).

753. Докажите, что при любых значениях переменной значение выражения:

а) З (х ²— х + 1) — 0,5х (4х — 6) является положительным числом; 2 б) у(2 + у — у ^з) — —(6 + Зу + 1,5у ²) является отрицательным з

числом.

754. Решите уравнение:

б) 7(2у - 2) - 2(3у - 3,5) = 9;

в)- 1) + - 9х) 82;

г)- 1) + 132,4 = (2,8 - • 0,5;

д)

2 з 9

1 — 6х 2х + 19 23 - 2х

2 12 з

157

755. Два сосуда были наполнены растворами соли, причём во втором сосуде содержалось на 2 кг больше раствора, чем в первом. Концентрация соли в первом растворе составляла 10 ⁰/0, а во втором — 30 ⁰/0 . После того как растворы слили в третий сосуд, получили новый раствор, концентрация соли в котором оказалась равной 25 ⁰/0 . Сколько раствора было в первом сосуде первоначально?

756. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая 200 кг. Через З ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?

757. Расстояние между пристанями М и л^травно 162 км. От пристани М отошёл теплоход со скоростью 45 км/ч. Через 45 мин от пристани навстречу ему отошёл другой теплоход, скорость которого 36 км/ч. Через сколько часов после отправления первого теплохода они встретятся?

758. От пристани А отошёл теплоход со скоростью 40 км/ч. Через

1— ч вслед за ним отошёл другой теплоход со скоростью

60 км/ч. Через сколько часов после своего отправления и на каком расстоянии от А второй теплоход догонит первый?

Из города А в город В одновременно отправляются два автобуса. Скорость одного из них на 10 км/ч больше скорости другого. Через З— ч один автобус пришёл в В, а другой находился от В на расстоянии, равном — расстояния между А и В. Найдите скорости автобусов и расстояние от А до В.

Из А в В одновременно выехали два мотоциклиста. Скорость одного из них в 1,5 раза больше скорости другого. Мотоциклист, который первым прибыл в В, сразу же отправился обратно. Другого мотоциклиста он встретил через 2 ч 24 мин после выезда из А. Расстояние между А и В равно 120 км. Найдите скорости мотоциклистов и расстояние от места встречи до В.

761. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2 ч против течения. Какова скорость катера в стоячей воде, если скорость течения 1,5 км/ч?

762. За 6 ч катер проходит по течению на 20 км меньше, чем за 10 ч против течения. Какова скорость течения, если скорость катера в стоячей воде 15 км/ч?

763. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до срока. Сколько сорочек в день должен был выпускать кооператив?

158	Глава lV

На элеватор поступило 1400 т пшеницы двух сортов. При обработке пшеницы одного сорта оказалось 2 ⁰/0 отходов, а другого сорта — 3 ⁰/0 отходов. Чистой пшеницы получилось 1364 т. Сколько пшеницы каждого сорта поступило на элеватор?

765. Бригада предполагала убирать 80 га пшеницы в день, чтобы закончить работу в намеченный ею срок. Фактически в день она убирала на 10 га больше, и поэтому за один день до срока ей осталось убрать 30 га. Сколько гектаров пшеницы должна была убрать бригада?

водный раствор соли массой 480 г добавили 20 г соли. В результате концентрация раствора повысилась на З, 75 ⁰/0 . Сколько соли было в растворе первоначально? 767. Разложите на множители:

а) а ²⁰— + 0 ⁵, а ⁸— а ^б,

б) b60 + b40 _ но. г) + b20 + b10

768. Докажите, что:

а) 7 ¹⁶+ 7 ¹⁴делится на 50;

б) 5 ³¹— 5 ²⁹делится на 100;

в) 25 ⁹+ 5 ¹⁷делится на 30;

г) 27 ¹⁰— 9 ¹⁴делится на 24;

д) 12 ¹³— 12 ¹²+ 12 ¹¹делится на 7 и на 19; 11 ⁹— 11 ⁸+ 11 ⁷делится на З и на 37. 769. Разложите на множители:

а) (а — 3b)(a + 26) + 5а(а + 26); 6) (х + - 5b) - 8у(2х - 56);

в) 7а ²(а — х) + (ба ²— ах)(х — а);

г) 11b ²(3b - у) - (бу - - З».

770. Найдите значение выражения:

а) 5сх + с ²при х = 0,17, с = 1,15;

б) 4а ²— ab при а = 1,47, Ь = 5,78. 771. Решите уравнение:

а) 1,2х ²+ х = о; в) 0,5х ²— х = О; д) 1,6х ²= 3х

б) 1,6х + х ²= О; г) 5х ²= х; ф] Вынесите за скобки числовой множитель:

а) (За + 6) ²; в) (7х + 7у) ²•, д) (5q — 30) ³; 6) (126 - 4) ²; г) (—3р + 6) ³; е) (2а - 8)⁴.

Докажите, что значение выражения а ²— а кратно 2 при любом целом а.

Докажите, что если к целому числу прибавить его квадрат, то полученная сумма будет чётным числом.

[26) Докажите, что разность чисел abc и cba, где а О, с О, кратна 11.

159

а) сумма трёх последовательных степеней числа 2 с натуральными показателями делится на 14; б) сумма двух последовательных степеней числа 5 с натуральными показателями делится на 30.

К параграфу 1 1

777. Докажите, что выражение тождественно равно некоторому двучлену:

а) (х + у)(х ²— ху + у ²);

б) (х — у)(х ²+ ху + у ²);

в) (а + Ь) (а ^з— a ²b + ab ²— Ы);

г) (а — Ь) (а ^з+ a ²b + ab ²+ Ы).

778. Упростите:

+ 26) + (1 +

в) 2х ²— (х — 2у)(2х + у);

г) (т — Зп)(т + 2n) — т (т — п);

д) (а - + 4а) - 7b(a + Ь);

е) (р — q)(p + 3q) — (р ²+ 3q ²).

779. Докажите, что выражение (у + 8)(у — 7) — 4 (0,25у — 16) при любом значении у принимает положительные значения.

Докажите, что значение выражения:

а) (3 ⁵— 3 ⁴) (3 ³+ 3 ²) делится на 24;

б) (2 ¹⁰+ 2 ⁸) (2 ⁵— 2 ³) делится на 60;

в) (16 ³— 8 ³) (4 ³+ 2 ³) делится на 63;

г) (125 ²+ — 1) делится на 39.

781. Упростите выражение и найдите его значение при указанных значениях переменных:

а) 126у ³+ (х — 5у)(х ²+ 25у ²+ 5ху) при х = —3, у — —2;

б) т ^з+ п ^э— (т ²— 2mn — — п) при т = —3, п = 4.

782. Докажите, что значения выражения не зависят от значения переменной:

а) (а — З)(а ²— 8а + 5) — (а — 8)(а ²— За + 5); 6) (х ²- 3х + + 5) - (2х ²+ 7х + - 4);

в) (6 ²+ - - 2) + (3 - + 5b + 2).

783. Докажите, что:

а) сумма пяти последовательных натуральных чисел кратна 5; б) сумма четырёх последовательных нечётных чисел кратна 8.

784. Найдите четыре последовательных натуральных числа, если известно, что произведение первых двух из этих чисел на 38 меньше произведения двух следующих.

160	Глава lV

785.

а) произведение двух средних из четырёх последовательных целых чисел на 2 больше произведения крайних чисел;

б) квадрат среднего из трёх последовательных нечётных чисел на 4 больше произведения двух крайних чисел.

786. Сторона квадрата на 2 см больше одной из сторон прямоугольника и на 5 см меньше другой. Найдите площадь квадрата, если известно, что она на 50 см ²меньше площади прямоугольника.

787. Если длину прямоугольника уменьшить на 4 см, а ширину увеличить на 5 см, то получится квадрат, площадь которого больше площади прямоугольника на 40 см ². Найдите площадь прямоугольника.

788. Периметр прямоугольника равен 36 м. Если его длину увеличить на 1 м, а ширину увеличить на 2 м, то его площадь увеличится на 30 м ². Определите площадь первоначального прямоугольника.

789. Периметр прямоугольника равен 30 см. Если его длину уменьшить на З см, а ширину увеличить на 5 см, то площадь прямоугольника уменьшится на 8 см ². Найдите площадь первоначального прямоугольника.

790. Найдите значение выражения:

а) а ²+ ab — 7а — 7b при а = 6,6, Ь = 0,4;

б) х²— ху — 4х + 4у при х = 0,5, у = 2,5;

в) 5а ²— 5ах — 7а + 7х при а = 4, х = —3;

г) хь — хс + Зс — 3b при х = 2, Ь = 12,5, с = 8,3;

д) ау — ах — 2х + 2у при а = —2, х = 9,1, у = —6,4;

е) Зах — 4by — 4ау + 3bx при а = З, Ь = -13, х = -1, у = -2.

791. Разложите на множители многочлен:

а) а ^з— 2а ²+ 2а — 4;

б) х^з— 12 + 6х²— 2х;

в) с ⁴— 2 с.2 + сз — 2с; 6 5 4 з.

д) a ²b — b ²c + а ²с — bc ²;

е) 2х ³+ ху ²— 2х ²у — у ^з;

ж) 16ab ²— 10с ³+ 32ас ²— 5b ²c;

з) ба ^з— 21a ²b + 2ab ²— 7b ³

792. Представьте в виде произведения:

а) та — ть + па — пь + ра — pb;

б) ах — bx — сх + ау — by — су;

в) х²+ ах ²— у — ау + сх ²— су;

г) ах ²+ 2у — bx ²+ ау + 2х²— by.

793. Разложите на множители многочлен:

а) - 10х + 24; в) х ²+ 8х + 7;

б) х ²— 13х + 40; г) х ²+ 15х + 54;

Макарычев, 7 кл. 161

а) а(х + 6) + х(х — За) = 9 при х = 2а — З;

б) х(х — За) + а(а + х) +4= 13 при х = а + З. ДОКаэките тождество:

а) (у⁴+ у³)(у ²— у) = у^а(у + 1)(у — 1);

б) (а ²+ За)(а ²+ За + 2) = а(а + 1)(а + 2)(а + З);

в) (а ²+ ab + — ab + b²) = а ⁴+ a²b²+ b⁴;

При каком значении а произведение

(х^з+ 4х²— 17х + 41)(х + а) тождественно равно многочлену, не содержащему х^а?

162	Глава lV

Докажите, что если Ь + с = 10, то

100а(а + 1) + bc.

Воспользовавшись этой формулой, вычислите:

а) 23 • 27; 6) 42 • 48;

Докажите, что:

а) если ab + с ²= О, то (а +

б) если а + Ь = 9, то (а +

в) 59 • 51; г) 84 • 86.

+ с) + (а — — с) = О

+ 1) — (а — 1)(b — 1) = 18.

В этой главе вы узнаете об интересных тождествах, с помощью КОТОРЫХ проще выполнять преобразования различных выражений. Эти тождества получили специальное название — формулы сокращённого умножения. Они широко используются для представления целого выражения в виде многочлена и разложения многочленов на множители. В старших классах вы научитесь применять их в преобразованиях более сложных выражений. Завершает главу параграф, в котором находят применение все изученные правила преобразования выражений. Вы научитесь приводить многочлен с одной переменной к виду, удобному для нахождения его значения с помощью калькулятора.

——ммы И КВАДРАТ РАЗНОСТИ

32. Возведение в квадрат и в куб суммы и разности двух выражений

При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого. Однако в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращённого умножения.

Возведём в квадрат сумму а + Ь. Для этого представим выражение (а + в виде произведения (а + Ь) (а + Ь) и выполним умножение:

(а + + Ь) = а ²+ ab + ab + Н =

= а ²+ 2ab + У.

Значит,

(а +

+ 2аь + Н.

(1)

163

Тождество (1) называют формулой кваДрата суммы. Эта формула позволяет проще выполнять возведение в квадрат суммы любых двух выражений:

квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго I выражений плюс квадрат второго выражения,

В «Началах» Евклида справедливость равенства

(а + = а ²+ 2ab + b²

при положительных значениях а и Ь доказана геометрически с помощью чертежа, приведённого на рисунке 70.

Возведём в квадрат разность а — Ь, получим

(а — Ь) (а — Ь) = а ²— ab — ab + b ²= = а ²— 2ab + Н.

Значит,

Рис. 70 (а — = а²— 2ab + b ². (2)

Тождество (2) называют формулой кваДрата разности. Она позволяет проще возводить в квадрат разность любых двух выражений:

квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второ- I го выражений плюс квадрат второго выражения.

Заметим, что тождество (2) можно получить из тождества (1), если представить разность а — Ь в виде суммы а + (—b):

(а + = а ²+ 2a(—b) + (—b) ²= а

Приведём примеры применения формул квадрата суммы и квадрата разности.

Пример 1. Возведём в квадрат сумму 8х + З.

По формуле квадрата суммы получим

(8х + = (8х) ²+ 2 • 8х • з + 3 ²= 64х ²+ 48х + 9. Пример 2. Возведём в квадрат разность 10х — у.

Воспользовавшись тождеством (2), получим

(10х — — (10х) ²— 2 • 10х • у + у ²= 100х ²— 20ху + у ².

164

Пример З, Представим в виде многочлена выражение (—5а —

Выражение (—5а — тождественно равно выражению (5а + 4) ². Действительно, при любом а значениями выражений —5а — 4 и 5а + 4 являются противоположные числа, а квадраты противоположных чисел равны. Получаем

(—5а — = (ба + = 250 ²+ 40а + 16.

Пример 4. Упростим выражение 2х(3 + 8х) — (4х — » 2х(3 + 8х) - (4х - = 6х + 16х ²- (16х ²- 4х + 0,25) = = 6х + 16х ²- 16х ²+ 4х - 0,25 10х - 0,25.

Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности. Имеем

= а ^з+ 2a ²b + ab ²+ a ²b + 2ab ²+ b ³= а ^з+ За ²Ь + Зан + Ы

Следовательно,

(а + = + За ²Ь + ЗаЬ²+ Ы. (3) Тождество (З) называют формулой куба суммы.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

Аналогично можно получить, что

(а — = а ^з— За ²Ь + ЗаЬ ²— Ь³ (4) Тождество (4) называют формулой куба разности.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого вы- , ражения и квадрата второго минус куб второго выражения.

•мк.«ч

165

Заметим, что тождество (4) можно получить из тождества (З), если разность а — Ь представить в виде суммы а + (—b).

Пример 5. Возведём в куб сумму 2х + З.

Имеем

(2х + = (2х) ³+ • 3 + 3 • 2х • 3 ²+ 3 ³=

= 8х ³+ 36х ²+ 54х + 27.

Пример 6. Возведём в куб разность 3х — 5.

Имеем

(3х - = (3х) ³- • 5 + 3 • 3х • 5 ²- 5 ³=

27х ³- 135х ²+ 225х - 125.

799. Представьте в виде многочлена:

а) (х + у) ², е) (9 — у)2,

ж) (а + 12) ²;

з) (15 — х) ²,

г) (10 — с) ²,

к) (0,3 — т) ².

800. Преобразуйте в многочлен:

а) (т + п) ², д) (а — 25) ²;

е) (40 + 02;

ж) (0,2 — х) ²,

Рис. 71

г) (8 — а) ²,

801. С помощью рисунка 71 разъясните геометрический смысл формулы (а — = а ²— 2ab + для положительных а и Ь, удовлетворяющих условию а > Ь.

802. Проверьте, что равенство

(п — + (п + + (п + + 10

верно при п = З. Покажите, что это равенство верно при ЛНУ бом п.

803. Преобразуйте выражение в многочлен:

а) (2х + 3)2; г) (5у — 4х) ²; ж) (0,3х — 0,5а) ²;

з) (10с + 0,10 ².

в) (10 + 80 ²;

166

804. Преобразуйте в многочлен:

а) (7 - 80 ²;д) (0,1m + 5n) ²;

6) (0,6 + 2х) ²;е) (120 - 0,30 ².

805. Преобразуйте в многочлен:

б) (—г — 2) ²; в) (—n + 4) ²; г) (—т — 10) ².

806. Из выражений (у — х) ², (у + х) ², (—у + х) ², (—х + у) ², (—х — выберите те, которые тождественно равны выражению:

а) (х + у) ², б) (х — у) ².

807. Докажите тождество:

= (Ь — а) ²,

808. Представьте в виде многочлена квадрат двучлена:

а) (—9а + 4b) ²• в) (—0,8х — д) (0,08а — 5002; 6) (-11х - 7у) ²; г) 1 6q)2 е) (—0,5х — 60у)2.

809. Преобразуйте в многочлен:

а) (-30 + 100 ²; в) (8х д) (—0,2р — 10q) ²;

б) (—6m — п) ², (50 е) (0,8х -

810. Используя формулу квадрата суммы или формулу квадрата разности, вычислите:

а) (100 + 1) ²•, в) 61 ²; д) 999 ²; ж) 9,9 ²;

6) (100 - 1) ²; г) 199 ²; е) 702 ²; з) 10,2 ².

811. Выполните возведение в квадрат:

а) (х²— 5) ²; 6) (7 - у ^зу, в) (2а + b ⁴) ²; г) (—3р + q ⁸) ².

812. Преобразуйте в многочлен:

а) (а ²— За) ²;

б) —х ³+ 6х г) (4у ³—

д) 1—а ⁵+ 8а ²

е) (0,66 — 60b2)2.

813. Представьте в виде многочлена:

а) (а ²— 2b) ²; б) (х ^а+ Зу ⁴) ²; в) (7а ⁶+ 12а)²; г) (15х — х ³) ²,

814. Замените знак * одночленом так, чтобы получившееся равенство было тождеством:

а) а ²+ 4ab + 4b ²;

б) (3х + = 9х ²+ бах + а ²;

в) (-к — 100 — 40m+ 4m²;

167

815. Упростите выражение:

а) (12а—

6) (2а+6Ь) ²-24аЬ; г) a2b2 —(ab— 7)2; е) а ⁴—81 —(а2 + 9)2.

816. Представьте в виде многочлена:

а) 18а + (а — 9) ²; в) 4х ²— (2х — 3) ²; 6) (5х - - 25х ²; г) (а + 2b) ²— 4b ².

817. Упростите выражение:

6) (20 + - 5(4а + 5); д) (а + 3)(5 — а) — (а — 1) ²;

в) 9b(b - 1) - + 2) ²•,(5 — 2у)2.

818. Упростите выражение и найдите его значение:

а) (х — 10) ²— х (х + 80) при х = 0,97;

б) (2х + — х (4х + 31) при х = —16,2;

в) (2х + — (2х — при х = —3,5;

г) (0,1х — + (0,1х + при х = —10.

819. Решите уравнение:

г) 16у(2 — у) + (4у — = О

820. Найдите корень уравнения:

а) (х — 5) ²— х ²= З; в) 9х ²— 1 —

6) (2у + - 4у ²= 5; г) х + (5х + = 25(1 + х ²).

821. Представьте в виде многочлена выражение:

а) 7(4а - 1) ²; г) З (а — + 8а;

б) —3 (5у — х) ², д) 98 - 4 + - 2) ²;

в) -10 -b+2 е) 10аь - 4(2а - + 6b ²

822. Преобразуйте в многочлен выражение:

а) яза + 0 ²; в) —3(2 — - 10х;

б) —6(4 — Ь)2; г) 12а ²— 4 (1 — 2а) ²+ 8.

823. Представьте в виде многочлена:

а) а (а + 902; в) (а + 2)(а — 1) ²;

б) 6х(х ²+ 5х) ²; г) (х — 4)(х + 2) ².

824. Докажите тождество:

а) (а + + (а — = 2(а ²+ b ²);

— (а — Ь)? = 4ab; (а + — 2ab;

г) (а + — 2b(a + Ь) = а ²— b ²

[$5) Докажите тождество Диофанта (III в.):

(а2 + + d2) = (ас + bd)2 + (ad — bc)2.

168

826. При каком значении х:

а) квадрат двучлена х + 1 на 120 больше квадрата двучлена х — З;

б) квадрат двучлена 2х + 10 в 4 раза больше квадрата двучлена

827. Пользуясь формулой куба суммы, преобразуйте в многочлен выражение: а) (а + 2) ³; б) (2х + у) ³; в) (а + 3b) ³.

828. Пользуясь формулой куба разности, преобразуйте в многочлен выражение: а) (Ь — 4)³; б) (1 — 2с)³; в) (2а — 3) ³.

829. Упростите выражение:

6) (а - 2b) ³+ баЬ(а - 26).

830. Запишите в виде выражения:

а) разность квадратов 2m и 7 п;

б) квадрат разности х и 8у;

в) утроенное произведение ба и 6²•

г) произведение суммы а и Ь и их разности.

831. Разложите на множители многочлен а ^з+ 2а + а ²+ 2.

832. Из пунктов А и В, расстояние между которыми 1020 км, отправились одновременно навстречу друг другу два поезда, причём скорость одного была на 10 км/ч больше скорости другого. Через 5 ч поезда, ещё не встретившись, находились на расстоянии 170 км друг от друга. Найдите скорости поездов.

33. Разложение на множители с помощью формул квадрата суммы и квадрата разности

Формулы квадрата суммы и квадрата разности находят применение не только для возведения в квадрат суммы и разности, но и для разложения на множители выражений вида а²+ 2ab + 6 ²и а ²— 2ab + b ²

Действительно, поменяв местами в этих формулах левую и правую части, получим а ²+ 2ab + b ²= (а + Ь)²; а ²— 2ab + b²= (а — Ь) ².

Приведённые равенства показывают, что трёхчлен а ²+ 2аЬ + 6 ²можно представить в виде произведения (а + Ь) (а + Ь), а трёхчлен а²— 2ab + b ²можно представить в виде произведений (а — Ь) (а — Ь).

Пример 1. Представим трёхчлен 9х ²+ 30х + 25 в виде квадрата двучлена.

Первое слагаемое представляет собой квадрат выражения 3х, третье — квадрат числа 5. Так как второе слагаемое равно

169

удвоенному произведению 3х и 5, то этот трёхчлен можно представить в виде квадрата суммы 3х и 5:

9х ²+ 30х + 25 = + 2 3х • 5 + 5 ²= + 5) ².

Пример 2. Разложим на множители трёхчлен а ²— 20ab ²+ 1008. Здесь можно применить формулу квадрата разности: а ²— 20ab ²+ 1008 =

= - 2 . а . 108 + = (а — 10b2)2 = (а — — 108).

833, Представьте трёхчлен в виде квадрата двучлена:

а) х ²+ 2ху + у ²; в) + 12а + 36;

б) р2 — 2pq + q2; г) 64 + 16b + b ²;

834. Представьте трёхчлен в виде произведения двух одинаковых множителей:

а) 4х ²+ 12х + 9; г) — т ²+ 4n ²— 2mn; 6) 258 + 10b + 1; д) 10ху + 0,25х ²+ 100у ²;

в) 9х ²— 24ху + 16у ²; е) 9а ²— ab+ —b ²36

835. Преобразуйте трёхчлен в квадрат двучлена:

а) 81а ²— 18ab+ b ²; в) 8ab+b ²+ 16а ²; д) b ²+ 4a ²—4ab;

б) 1 +у ²— 2у; г) 100х ²+ у ²+ 20ху; е) 28ху +49х ²+ 4у ².

836. Поставьте вместо знака * такой одночлен, чтобы трёхчлен можно было представить в виде квадрата двучлена:

а) * + 560 + 49; в) 250 ²+ * + _b2;

6) 36 - 12х + г) 0,018 + * + 1008

837. Впишите вместо знака * недостающие одночлены так, чтобы получилось тождество:

а) ( * + 2а) ²= * 12ab + б) (3х + = * + * + 49у2.

838. Замените знак * таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена:

а) Ь ²+ 20b * ; в) 16х ²+ 24ху + •к;

г) * — 42pq + 49q ².

839. Представьте трёхчлен в виде квадрата двучлена или в виде выражения, противоположного квадрату двучлена:

а) —1 + 4а — 4а ²;

б) —42а + 9а ²+ 49;

170

в) 24аЬ - 168 - 98;

г) —44ах + 121а ²+ 4х ²;

д) 4cd — 258 — 0,16d ²;

е) —0,49х ²— 1,4ху — у ².

840. Найдите значение выражения:

а) у ²— 2у + 1 при у = 101 ; —11; 0,6;

б) 4х ²— 20х + 25 при х = 12,5; О; —2;

в) 25а ²+ 49 + 70а при а = 0,4; —2; —1,6.

841. Верно ли, что при любых значениях х:

а) х ²+ 10 > О; 6) .r ²+ 20х + 100 > 0?

842. Сравните с нулём значение выражения:

а) х ²- 30х + 225; б) —х ²+ 2ху — у².

843. Поставьте вместо многоточия какой-либо из знаков или так, чтобы получившееся неравенство было верно при любом

значении х:

а) х ²— 16х + 64 ... О;

6) 16 + + х ²... О; г) —х ²+ 18х — 81 .

844. Представьте выражение в виде квадрата двучлена, если это возможно:

а) —х2 + 3х + 9;

6) 250 ²- зоаь + 98;

в) р ²— 2р + 4;

г) —х ²+ — ху + — у ^а,

15 25

д) 1008 + 98 - 60bc•,

е) 49х ²+ 12ху + 64у ².

845. Преобразуйте выражение в квадрат двучлена:

а) х ⁴— 8х²у ²+ 16у⁴; в) —а ²+ 2ab ²+ 4b ⁴;

б) —х ⁴+ 2х ²а + 16а ²; г) 0 ²х ²— 2abx + 6 ²16

846. Разложите на множители трёхчлен:

а) 4а ⁶— 4a ³b ²+ Ы; б) b ⁸— a ²b ⁴+ —а ⁴.

Докажите, что при любом значении х многочлен х ²+ 6х + 10 принимает положительные значения.

[Ц Докажите, что выражение принимает лишь положительные значения:

б) 4у ²— 4у + 6;

в) а ²+ b ²— 2ab + 1;

г) 9х ²+ 4 — бху + 4у².

849. Прочитайте выражение:

а) (а — 10b) ²; 6) - (100 ²; в) (а + 10b)(a — 10).

850. Запишите в виде выражения:

а) квадрат суммы За и — Ь;

б) сумму квадратов 0,5m и 5,3n;

в) произведение 0,6х ²и 9у ².

171

851. Представьте в виде многочлена:

а) (х²+ 4ху — у²)(2у — х); в) (а²— 4ab + — Ь);

б) (З — а) (а^з— 4а²— 5а); г) (х — р) (х²+ рх + р²).

852. Представьте выражение в виде квадрата одночлена:

а) 4х⁴; в) Збт ^б; д) 9a4b2;

6) 0,250⁴; г) a²b⁴• е) 0,16х⁶у⁴.

853. Преобразуйте в многочлен выражение: а) (З + а)

Контрольные вопросы и задания

Напишите формулу квадрата суммы.

Напишите формулу квадрата разности. Приведите пример трёхчлена, квадрата суммы.

Приведите пример трёхчлена, квадрата разности.

Напишите формулу куба суммы.

Напишите формулу куба разности.

Проведите доказательство. Проведите доказательство. который можно представить в виде

который можно представить в виде

Возведите в куб двучлен а + 2b. Возведите в куб двучлен 3х — у.

РАЗНОСТЬ КВАДРАТОВ.

СУММА И РАЗНОСТЬ КУБОВ

34. Умножение разности двух выражений на их сумму

Рассмотрим ещё одну формулу сокращённого умножения. Умножим разность а — Ь на сумму а + Ь:

(а — + Ь) = а ²+ ab — ab — b²= а ²— b ²

Значит,

(а — Ь) (а + Ь) = а²— Ь². (1)

Тождество (1) позволяет сокращённо выполнять умножение разности любых двух выражений на их сумму:

произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

172

Приведём примеры применения формулы (1).

Пример 1. Умножим разность 3х — 7 у на сумму 3х + 7у.

Воспользовавшись тождеством (1), получим

(3х - + 7у) = (3х) ²- (7у) ²= 9х ²- 49у ².

Пример 2. Представим в виде многочлена произведение

(50 ²— + Ы).

Применив тождество (1), получим

(5а ²— + Ы) = (5а2)2 — (b ³) ²= 25а ⁴— b⁶.

П р имер З. Представим в виде многочлена произведение

(—2а — 9с) (2а — 9с).

Вынесем в выражении —2а — 9с за скобки —1, тогда

(-20 - - 9с) = + - 9с) = = -((2а) ²- (902) = -(4а ²- 818) = -40 ²+ 818

Преобразование можно выполнить иначе:

(-9с - + 20) = (-90 ²- (2а) ²= 818 - 40 ².

Пример 4. Упростим выражение 6,5х ²— (2х + 0,8) (2х — 0,8). Имеем

6,5х ²- (2х + 0,8) (2х 0,8) = 6,5х ²- (4х ²- 0,64) = = 6,5х ²- 4х ²+ 0,64 = 2,5х ²+ 0,64.

854. Выполните умножение многочленов:

а) (х—у)(х+у); д) (2х— 1);

е) (7+30 (Зу — 7);

855. Выполните умножение:

		а

а) (у — 4)(у + 4);

в) (4 + 5у)(5у — 4);

д) (86 + 5а)(5а — 86);

е) (10х — 6с)(1Ох + бс).

856. С помощью рисунка 72 разъясните геометрический смысл формулы (а — + Ь) = а ²— 6 ²для положительных а и Ь, удовлетворяющих условию а > Ь. Рис. 72

173

857. Представьте в виде многочлена произведение:

а) (х²— 5) (х²+ 5); е) (аз — Н) (аз + b2);

б) (4 + у²) (у²— 4); ж) (с⁴+ d²) (d²— с⁴);

в) (9а — b²) (b²+ 9а); з) (5х²+ 2у³) (5х²— 2у³);

г) (0,7х + Г) (0,7х - и) (1,4с- 1,40;

д) (10р²— + 0,3q²); к) (1,30 - о, 18) (1,30 + о, 18).

858. Впишите вместо знака * одночлен так, чтобы получилось тождество:

а) (2а + *)(2а — = 4а ²— Н;

б) — Зх)(* + 3х) = 16у2 — 9х2;

в) — + •к) = 1210 ¹⁰— b⁸•

г) т4 — 225с10 = (Т2 — + т2)•

859. Представьте в виде многочлена:

д) (0,4у ³+

е) (1,28 -

ж) (58

^г) ( ( 71

860. Найдите значение выражения:

а) (100 - 1)(100 + 1) г) 201 • 199; ж) 1,05 • 0,95; 6) (80 + - 3); д) 74 • 66; з) 60,1 • 59,9.

в) 64 • 56; е) 1002 • 998;

861. Найдите значение произведения:

а) 52 • 48;	г) 2,03 • 1,97;	ж) • 10,3;
6) 37 • 43;	д) 17,3 • 16,7;	з) 50,2 • 49,8;
в) 6,01 • 5,99;	е) 29,8 • 30,2;	и) 4,6 • 5,4.

862. Представьте выражение в виде многочлена, используя соответствующую формулу сокращённого умножения:

д) (х — у)(у — х);

863. Представьте в виде многочлена:

а) (—3ху + а)(Зху + а); г) (-10р⁴+ - 10р⁴);

б) (—1 — 2a ²b)(1 — 2a ²b); д) (0,2х + - 0,2х)•, - 7х); е) (1,1у - + 1,1у).

в) (6n ²+ 1) (—6n ²+ 1);

г) (-7аь - - 7аЬ).

865. Найдите наибольшее значение выражения:

•

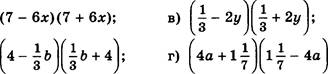866. Найдите наибольшее или наименьшее значение выражения, если такое значение существует:

в) аза - + 13а);

г) (10 — 9m)(9m + 10).

867. Представьте в виде многочлена:

г) —3а(а + 5)(5 — а);

б) у(у + 4)(у — 4); д) (0,5х -

в) 5х(х + 2)(х — 2); е) -5у(-Зу

868. Представьте выражение в виде многочлена:

а) (Ь + — ау, в) (а — 4)(а + 4)²;

г) (Зр + 1)²(1 — Зр).

869. Выполните умножение:

в) (а ²+ 1)(а + 1)(а — 1);

г) (с⁴+ 1)(с²+ 1)(с ²— 1); 870. Упростите выражение:

ж) (а — 5)²(5 + ау;

з) (с + — с)².

д) (х — З)²(х + 3)²;

е) (у + — 4)²;

а) (0,8х+ 15) +0,36х²; г) (За— 1)(За + 1) — 17а ²;

д) 100х²— + 5х);

в) 2х²— (х + 1); е) 228 +(-зс- 7).

871. Упростите:

а) (х — + у)(х²+ у ²); г) (зт — 2)(Зт + 2) + 4;

д) 25n ²— (7 + 5n)(7 — 5n);

в) (сз + — + Н); е) 6х²- (х - + 0,5).

872. Докажите, что квадрат любого целого числа на единицу больше произведения предыдущего и последующего целых чисел.

873. Упростите выражение:

б) т (т — 4) + (З — т)(З + т);

в) (4х — а)(4х + а) + 2х(х — а);

г) 2а(а + Ь) — (20 + - Ь);

д) (5а — Зс)(5а + Зс)

ж) (3х — 4у)²— (3х — 4у)(Зх + 4!);

ё и

874. (Для работы в парах.) Докажите, что сумма произведения трёх последовательных целых чисел и среднего из них равна кубу среднего числа.

1) Проверьте утверждение на примере чисел 19, 20, 21.

2) Составьте выражение, обозначив через р одно из этих чисел, и выполните преобразование составленного выражения. Одному учащемуся рекомендуем обозначить через р наименьшее из чисел, а другому — среднее из чисел.

З) Проверьте друг у друга правильность преобразований и сравните их сложность.

875. Упростите выражение:

а) 5а(а — 8) — З(а + 2)(а — 2);

876. Решите уравнение:

а) 8m(1 + 2m) — (4m + З)(4т — З) = 2m;

6) х - 3х(1 - 11 — (5 — бх)(бх + 5).

877. Найдите корень уравнения:

а) (6х — 1)(6х + 1) — 4х(9х + 2) —

б) —a ²b ²+ ab + 1.

b)2;

= 2х ³+ 54х.

3х - 1

• 2,4;

д) 0 69 • 13,8;

882. Со станций М и N, расстояние между которыми 380 км, одновременно навстречу друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам оставалось пройти до встречи 30 км. Найдите скорость поездов.

35. Разложение разности квадратов на множители

В тождестве (а — Ь) (а + Ь) = а ²— b ²поменяем местами правую и левую части. Получим а? — 6²= (а — Ь)(а + Ь).

Это тождество называют формулой разности кваДратов. Её применяют для разложения на множители разности квадратов любых двух выражений:

ЧТВЧ разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

Приведём примеры применения формулы разности квадратов.

Пример 1. Разложим на множители выражение 36 — а ².

Так как 36 = 6 ², то

36 — а ²= 6 ²— а ²= (6 — а)(б + а).

Пример 2. Представим в виде произведения двучлен 49х ²— 16у ⁶.

Данный двучлен можно представить в виде разности квадратов.

Получим

49х ²— 16у ⁶= (7х) ²— = (7х — 4у ³)(7х + 4у ³).

883. Разложите на множители многочлен:

а) х ²— у ²,

ж) р ²— 400;

— 22

д) 16 — 6 ²;

з) - 0,09;

л)

в) а ²— 25

е) 100 — х ²,

и) 1,44 а2.

м)

177

884. Разложите на а) 25х ²— у ²;

б) —т ²+ 16n ²;

в) Зба ²— 49;

г) 64 — 25х²;

885. Представьте в

а) х ²— 64; 6) 0,16 - 8, в) 121 — т ²,

886. Вычислите:

а) 47 ²- 37 ²;

6) 53 ²- 63 ²;

множители:

д) 9m ²— 16n ²;

е) 64р ²— 81q ²;

ж) —49а ²+ 16b ²;

з) 0,01n ²— 4m ²;

виде произведения:

г) -81 + 25у ²•,

д) 144b ²— 8;

е) 0,64х ²— 0,49у ²;

в) 126 ²- 74 ²;

г) 21,3 ²- 21,2 ²;

д)

е)

и) 9 — b2c2;

к) 4a ²b ²— 1; ^л) р²- а ²ь ²•

м) 16c ²d ²— 9а ².

ж) х ²у ²— 0,25;

з) c ²d ²— а ²

178

и) а ²х ²— 4у2.

0,849 ²- 0,151 ²;

2 5?

887. Найдите значение дроби:

36 79 ²- 65 ²532 _ 272 532 _ 322

а) 13²- 11²' б) 420 в) 792 _ 512 г) 61²- 44²

888. Найдите значение выражения: 262 _

а) 41 ²- 31 ²;

в) 256 ²- 156 ²;

д)

122

54²—

632 _

6) 76 ²- 24 ²;

г) 0,783 ²- 0,217 ²;

272

832

_ 792 •

889. Разложите на множители:

м) 81 — b⁴

890. Решите уравнение:

а) .r²— 16 = О; г)- 0,25 = о;

б) у ²— 81 = О; д)+ 36 = о;

891. Решите уравнение:

а) т ²— 25 = О; в) 9х ²- 4 = 0;

6) х ^а- 36 = о; г) 16х ²- 49 = о.

892. Представьте в виде произведения:

а) с ^б— 9Х⁴;

б) 100у ²— а ⁸;

в) 4х ⁴— 25b ²;

г) a ⁴b ⁴— 1

д) 0,36 — х ⁴у ⁴,

е) 4а2 — b6c2;

ж) 4х ²— 9 = О;

з) 25х ²- 16 = о;

и) 81х ²+ 4 = О.

ж) 16т ²у ²— 9n ⁴;

з) 9х ⁸у ⁴— 10022;

и) 0,81р ⁶т ⁴— 0,01х ².

893. Разложите на множители:

а) 64 — у⁴, г) 25m⁶— п²;

б) х²— с^е, д) 1 — 49р10;

в) а4 — Н. е) 4у⁶— 9а⁴;

ж) 64 — a ⁴b ⁴;

з) - 0,25;

и) 81х ⁶у ²— 0,36а ².

894. Представьте выражение в виде произведения:

в) (4а — — 16; д) (5у — — 81;

6) 64 - (Ь + 1)²; г) 25 - (а + 7)²; е) 1 - (2х - 1)².

895. Разложите на множители:

а) 9у²— (1 + 2у)²; г) (5а — 3b)²— 25а ²; 6) (3с - - 168; д) (—2а ²+ 3b) ²— 4а ⁴;

в) 49х²— (у + 8х)²; (х — 4b3)2.

896. Представьте в виде произведения:

а) (2b - - 36;	в) (4 — 11m) ²— 1;	д) (5с - 3d)²- 9d ²•,
6) 9 - (7 + за)²•,	г) р ²— (2р + 1) ²;	е) а ⁴— (9b + а ²) ².

897. Представьте в виде произведения:

а) (2х + — (х — 2у)²; в) (т + — (т — п) ²,

б) (а + — (Ь + су; г) (4с — х) ²— (2с + зх) ².

898. а) Докажите, что при любом натуральном п значение выражения (4n + 5)²— 9 делится на 4.

б) Докажите, что при любом натуральном п значение выражения (п + 7)²— п²делится на 7.

899. На сторонах прямоугольника построены квадраты (рис. 73). Площадь одного квадрата на 95 см ²больше площади другого. Найдите периметр прямоугольника, если известно, что длина прямоугольника на 5 см больше его ширины.

900. (ЗаДача-исслеДование.) Верно ли, что если р — простое число, большее трёх, то значение выражения р²— 1 кратно 12.

1) Проверьте правильность утверждения Рис. 73 на конкретных примерах.

2) Разложите многочлен р ²— 1 на множители. Обсудите, почему полученное произведение кратно 4.

З) Обсудите, почему полученное произведение делится на З. 4) Сделайте вывод.

Представьте в виде куба одночлена выражение:

а) 270 ³; в) 86⁶; д) —27а ⁸х ⁶;

б) —8m ³; г) —64р⁶; е) 64а ⁶х ⁹

5 и

902. Представьте многочлен в виде квадрата двучлена или выражения, противоположного квадрату двучлена:

а) 0,25х ²- 0,6ху + о,зу ²; в)

16 9

б) —а ²+ 0,6а — 0,09; г) —16m ²— 24mn — 9n ²

903. Решите уравнение:

а) (5х — 1)(2х + 1) — 10х ²= 0,8; 6) 18х ²- (9х + - 1) = 1.

904. Турист рассчитал, что если он будет идти к железнодорожной станции со скоростью 4 км/ч, то опоздает к поезду на полчаса, а если он будет идти со скоростью 5 км/ч, то придёт на станцико за 6 мин до отправления поезда. Какое расстояние должен пройти турист?

36. Разложение на множители суммы и разности кубов

Для разложения на множители суммы кубов используется тож-

дество а ^з+ Ы = (а + Ь) (а ²— ab + Н), (1)

которое называют формулой суммы кубов.

Чтобы доказать тождество (1), умножим двучлен а + Ь на трёхчлен а2 — ab + b2:

(а + — ab + b ²) =

= а ^з— a ²b + ab ²+ a ²b — ab ²+ b ³= а ^з+ Ы

Множитель а ²— ab + 6 ²в правой части формулы (1) напоминаег трёхчлен а ²— 2ab + b ², который равен квадрату разности а и Ь. Однако вместо удвоенного произведения а и Ь в нём стоит просто их произведение. Трёхчлен а ²— ab + b ²называют неполным кваДратом разности а и Ь. Итак,

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Пример 1. Разложим на множители многочлен 27х ³+ у ^з.

Данный многочлен можно представить в виде суммы кубов двух выражений:

27х ³+ у ^з= (3х) ³+ у ^з.

1 80

Применив формулу (1), получим

(3х) ³+ у ^з= (3х + у)(9х ²— 3ху + у ²).

Итак,

27х ³+ у ^з= (3х + у) (9х ²— 3ху +

Для разложения на множители разности кубов используется тождество а ^з— b ³= (а — Ь) (0 ²+ ab + b ²), (2)

которое называют формулой разности кубов.

Чтобы доказать тождество (2), преобразуем произведение двучлена а — Ь и трёхчлена а ²+ ab + 6 ², который называют неполным квадратом суммы а и Ь:

(а — + + 62) =

= а ^з+ a ²b + ab ²— a ²b — ab ²— 6³= а ^з— 6³

«пае. Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата „их суммы.

При мер 2. Разложим на множители многочлен т ^б— п ^з.

Представим данный многочлен в виде разности кубов двух выражений и применим формулу (2). Получим т ^б— п ^з= (т ²) ³— п ^з= (т ²— + т ²п + п ²).

905. Разложите на множители многочлен: з з.

б) з

906. Примените формулу суммы кубов или формулу разности кубов:

в) х^з— 64;

б) г) 125 + а ^з,

907. Представьте выражение в виде суммы или разности кубов и разложите его на множители:

1 а) 8х³— 1; в) 8 — — а ^зД) 125а ^З— 60 ³;

1 1

6) 1 + 27у ^з•, Г) Т ^З+ 1000;

6427 125

908. Разложите на множители:

а) 8 — т ^э, в) 64х³+ 1; д)

г) 1 — ^Ар ^з

1 81

Разность квадратов. и

909. Запишите в виде произведения выражение:

г) р8 + р.,

910. Разложите на множители:

в) х ^а— 8; Г) 27 +

911. Запишите в виде произведения:

1 а) —х^з+ у ^з, Д) сб + 1

6 6 27

912. Представьте в виде произведения:

а) a ³b ³— 1 зсз. 6 з з.

г) т ^зп ^з+ 27; ззп9

913. Докажите, что значение выражения:

а) 327 ³+ 173 ³делится на 500; в) 211 ⁸+ 129 ⁸делится на 17;

б) 731 ³— 631 ³делится на 100; г) 356 ³— 245 ³делится на З.

914. Делится ли значение выражения:

а) 38 ³+ 37 ³на 75; 6) 99 ³- 74 ³на 25?

915. Представьте в виде многочлена:

а) (118 + + 118); в) (0,зс - - О,ЗС);

б) (0,8х + Г) (—0,8х — у⁴); г) (6х ³— 4х)(—6х ^З— 4х).

916. Докажите, что равенство не является тождеством:

а) х ⁴+ 4 = (х + 2) ²; б) (х — 2)(2 + х) = 4 — х ².

917. Решите уравнение:

а) (2х - - 2х(4 + 11;

6) (4х - + 4х) - 2х(8х - 1) = о.

Контрольные вопросы и задания

Чему равно произведение разности Напишите соответствующую формулу

чему равна разность квадратов ветствующую формулу.

Напишите формулу суммы кубов.

Напишите формулу разности кубов.

Разложите на множители многочлен

двух выражений и их суммы? и докажите её.

выражений? Напишите соот-

Проведите доказательство.

Проведите доказательство. 16t ²— 1; + 8; т ^э— 27.

182

, ц—РАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ

37, Преобразование целого выражения в многочлен

Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, называют целыми выражениями (произведение одинаковых множителей в целом выражении может быть записано в виде степени). К целым относят и выражения, в которых, кроме действий сложения, вычитания и умножения, используется деление на число, отличное от нуля.

Многочлены и, в частности, одночлены являются целыми выражениями. Например, 3,5х ²у — 4ху ²+ 10х — 0,5у и —a ³bc ²— це-

лые выражения. Примерами целых выражений служат такие выражения:

10у ³+ (3х + у)(х ²— 10у ²), 2b(b ²— 10с ²) — (Н + 28),

За2 — + 2с) + 2, 5ас.

Выражение х + — 5(х — 1) не является целым, так как в нём 1 — х используется деление на выражение с переменной.

Выражение 10у ^з+ (3х + у) (х ²— 10у²) является суммой одночлена 10у ³и произведения многочленов 3х + у и х ²— 10у ². Выражение 2b(b ²- 10с ) — (Н + 28) является разностью между произведением одночлена 2b и многочлена b ²— 108 и многочленом Ы + 28. Мы знаем, что сумму, разность и произведение многочленов можно преобразовать в многочлен, поэтому каждое из этих целых выражений можно представить в виде многочлена.

Выражение 302 _ а(а + 2с) + 2, 5ас отличается от рассмотренных

тем, что в нём содержится деление на число, отличное от нуля. Если деление заменить умножением на число, обратное делителю, то получится выражение За ²— а (а + 2с) + 2, бас, которое, как и преды5 дущие выражения, составлено из многочленов с помощью действий сложения, вычитания, умножения. Поэтому это целое выражение также можно представить в виде многочлена.

i__члена.

Пример 1. Представим в виде многочлена выражение

Имеем

(х⁴+ 4х ²+ 4) — (х ²— 4)(х ²+ 4) = х⁴+ 4х ²+ 4 — х⁴+ 16 = 4х ²+ 20.

Значит, данное выражение тождественно равно многочлену 4х ²+ 20.

Преобразование целого выражения в многочлен используется при решении уравнений, доказательстве тождеств, в задачах на делимость и т. п.

П р и мер 2. Докажем, что ни при каком целом п значение выражения (п + 1)(n — 1) — (п — б)(п + 2) не делится на 4.

Упростим данное выражение:

(п + 1)(n — 1) — (п — б)(п + 2) = (п ²— 1) — (п ²— бп + 2n — 12) = — — 1 — п ²+ бп — 2n + 12 = 4n + 11.

Мы представили данное выражение в виде суммы 4n + 11. При любом целом п значение первого слагаемого делится на 4; второе слагаемое — число 11 — не делится на 4. Поэтому при любом целом п значение суммы 4n + 11, а значит, и значение исходного выражения (п + 1)(n — 1) — (п — б)(п + 2) не делится на 4. <

918. Какие из выражений 2х ²у, 4а ²— b(a — 3b), 9х — 2 являются целыми?

919. Представьте в виде многочлена:

а) сумму многочлена х ^з+ 7х ²+ 8 и произведения многочленов х ²— 6х + 4 и х — 1;

б) разность произведения многочленов а ²+ 7а — 4 и а — З и многочлена а ^з+ 4а ²— 29а + 11.

920. Преобразуйте в многочлен:

а) 4(m — + 4m(m — п);

б) 5х(х — у) — 2 (у — ху, г) (х — 5)(6 + 4х) — З (1 — х) ².

921. Упростите выражение:

а) (зт — а)(а + Зт) — (2а + т)(За т);

б) (х — 4у)(х + Зу) + (х — Зу)(Зу + х).

922. Зная, что а = 2х — 5, Ь = 8х + 1, с = 4х — 2, представьте в виде многочлена с переменной х выражение ab — 8.

923. Докажите, что ни при каком целом п значение выражения

(5n + 13) не делится на 6.

184

924. (Для работы в парах.) Впишите вместо многоточия в выражение

(п + 8)(n — 4) — (п + З)(п — 2) + ...

пропущенное число так, чтобы получилось выражение, значение которого при любом целом п делится на З.

1) Преобразуйте в многочлен каждое из произведений двучленов и выполните вычитание.

2) Обсудите друг с другом, какому условию должно удовлетворять пропущенное число.

З) Впишите вместо многоточия каждый какое-либо число, удовлетворяющее условию задачи.

4) Проверьте друг у друга, правильно ли выполнено задание.

925. Решите уравнение:

а) х(х + 2)(х — 2) — х(х²— 8) = 16; 6) 2у(4у - 1) - - 2у)²= 48.

926. Решите уравнение:

а) х²(х + 2) — х(х + 1)²= 5х + 9;

927. Докажите, что значение выражения не зависит от значения переменной:

а) (а - + + 1) - - - 2(а ²- 3);

185

б) (а2 — _ (а — 2)(а ²+ 4)(а + 2) — 6(5 — а ²).

928. Упростите выражение:

а) (у - + + 3) - (2у ²- - 19;

б) (1 — а)(1 — а ²) + (1 + а)(1 + а ²) — 2а(1 + а)(а — 1).

929. Докажите тождество:

а) (а - + 20) + зс(а + зс) -— (2а — с)(Зс + 5а) — 8а ²; 6) (1 - - 5b + 6 ²) + (2b - - + Ь²) = - 2b).

930. Представьте данный трёхчлен, если это возможно, в виде квадрата двучлена или в виде выражения, противоположного квадрату двучлена:

а) 25у ²— 15ау + 9а ²; в) 4b ²+ 0,258 - 2bc•,

б) 15ab — 9а2 — 6 ! 62; г) 0,360 ²+ 0,04$ - 0,24ау.

931. Разложите на множители:

а) —20х⁴у ²— 35х³у ³; в) —1,2a ³b + 1,2b ⁴;

б) За^ЗЬ ²с + 9ab ²c ³; г) 7,2х⁴у ⁴— 1,8х⁴у ².

932. От деревни до станции велосипедист ехал со скоростью 15 км/ч, а обратно он возвращался со скоростью 10 км/ч. Найдите расстояние от деревни до станции, если известно, что на обратный путь велосипедист затратил на 1 ч больше, чем на путь от деревни до станции.

933. Из пункта А связной доставил донесение в пункт В за 30 мин. На обратном пути он уменьшил скорость на 1 км/ч и затратил на дорогу 36 мин. Определите, с какой скоростью шёл связной из пункта А в пункт В.

38, Применение различных способов для разложения на множители

Для разложения многочленов на множители мы применяли вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Иногда удаётся разложить многочлен на множители, применив последовательно несколько способов. При этом начинать преобразование следует, если это возможно, с вынесения общего множителя за скобки.

Пример 1. Разложим на множители многочлен 10а ³— 400. Члены этого многочлена имеют общий множитель 10а. Вынесем этот множитель за скобки:

10а ³— 40а = 10а(а ²— 4).

Разложение на множители можно продолжить, применив к выражению а ²— 4 формулу разности квадратов. В результате получим в качестве множителей многочлены более низких степеней. Имеем

10а(а ²— 4) - — 10а(а + - 2).

Значит,

1Оа ^З- 40а = 10а(а + - 2).

Пример 2. Разложим на множители многочлен аЬ ³— 36 ³+ аЬ ²у — 3b ²y.

Сначала вынесем за скобки общий множитель 6 ²:

ab ³— 36 ³+ аЬ ²у — ЗЬ ²у = = b ²(ab — 36 + ау — Зу).

186

Попытаемся теперь разложить на множители многочлен ab — 3b + ау — Зу.

Сгруппировав первый член со вторым и третий с четвёртым, будем иметь ab — 3b + ау — Зу = — З) + у(а — З) =

Окончательно получим аЬ ³— ЗЫ + аЬ ²у — 3b ²y = Н (а — 3)(b + у). <

П р имер З. Разложим на множители многочлен а ²— 4ах — 9 + 4х ²

Сгруппируем первый, второй и четвёртый члены многочлена. Получим трёхчлен а ²— 4ах + 4х ², который можно представить в виде квадрата разности. Поэтому

а ²— 4ах — 9 + 4х ²= (а ²— 4ах + 4х ²) — 9 =

= (а - 2х) ²- 9.

Полученное выражение можно разложить на множители по формуле разности квадратов:

(а — 2х) ²— 9 = (а — 2х) ²— 3 ²— Следовательно, а ²— 4ах — 9 + 4х ²= (а — 2х — З)(а — 2х + З). <

Заметим, что при разложении многочлена на множители имеют в виду представление его в виде произведения нескольких многочленов, в котором хотя бы два множителя являются многочленами ненулевой степени (т. е. не являются числами).

Не каждый многочлен можно разложить на множители. Например, нельзя разложить на множители многочлены .r ²+ 1, 4х ²— 2х + 1 и т. п.

Рассмотрим пример использования разложения на множители для упрощения вычислений с помощью калькулятора.

П р и мер 4, Найдём с помощью калькулятора значение многочлена 5х ³+ 2х ²— 7х + 4 при х = 1,2.

Если выполнять действия в принятом порядке, то сначала придётся найти значения выражений х ³• 5, х ²• 2 и 7 х, записать результаты на бумаге или ввести их в память калькулятора, а затем перейти к действиям сложения и вычитания. Однако искомый результат можно получить гораздо проще, если преобразовать данный многочлен следующим образом:

5х ³+ 2х ²- 7х (5х ²+ 2х - ох + 4 = ((5х + - ох + 4.

Выполнив вычисления для х = 1,2, найдём, что значение многочлена равно 7,12.

187

934. Разложите на множители многочлен:

а) 5х ²— 5у ²; в) 2ах ²— 2ау ²; д) 16х ²— 4;

б) ат ²— ап ², г) 9р2 — 9; е) 75 - 278.

935. Представьте в виде произведения:

а) уз — .џ5' б) 2х — 2х³; в) 81х ²— х ^а; г) 4у ³— 100у ⁵.

936. Выполните разложение на множители:

а) тх ²— 49m; б) ab ²— 4ас ²; в) 4b ³— Ь; г) а ^з— ас ².

937. Докажите тождество а ⁸— b⁸= (а — Ь)(а + Ь) (а ²+ b ²) (а ⁴+ Ы).

938. Разложите на множители:

4 8

939. Разложите на множители:

а) 3х ²+ бху + Зу ²; г) бр ²+ 24q ²+ 24pq;

б) —т ²+ 2m — 1; д) 45х + ЗОах + 5а ²х;

в) —4х — 4 — х ², е) 18сх ²— 24сх + 8с.

940. Разложите на множители выражение х ⁶— у ^б, представив его в виде: а) разности квадратов; б) разности кубов.

941. Выполните разложение на множители:

а) 2m ²— 4m + 2; б) 36 + 24х + 4х ²; в) 80 ³— 86 ³; г) 9ах ³+ 9ау ³.

942. Разложите на множители:

а) 4ху + 12у — 4х — 12; в) —abc — 5ас — 4ab — 20а; 6) 60 + - ЗОЬ - 12а•, г) а ^з+ а ²Ь + а ²+ ab

943. Представьте в виде произведения:

а) 45b + ба - ЗаЬ - 90; в) ас ⁴

б) —5ху — 40у — 15х — 120; г) х ^з— х ²у + х ²— ху.

944. Выполните разложение на множители:

а) .r2 — 2хс + с2 _ d2. в) р ²— х ²+ 6х — 9;

б) с ²+ 2с + 1 — а ²; г) х ²— а ²— 10а — 25.

945 Разложите на множители:

а) х ²+ 2ху + у ²— т ²;

б) р ²— а ²— 2ab — b ²; г) 9 — с ²+ а? — ба.

946. Разложите на множители:

в) т + п + — п ²,

г) к ^г— К — р ²— р.

947. Представьте в виде произведения:

188

948. (Для работы в парах.) Используя калькулятор, найдите значение многочлена 3,5х ³— 2,1х ²+ 1,9х 16,7 при х = 3,7.

1) Пусть один из вас вычислит с помощью калькулятора сначала значения каждого члена многочлена, затем значение многочлена, а другой выполнит преобразование многочлена по образцу, предложенному в примере 4 на с. 187, затем сделает вычисления с помощью калькулятора.

2) Отметьте затрату времени на выполнение задания в каждом случае.

З) Сравните полученные результаты и время, затраченное на решение задачи.

949. Решите уравнение:

б) 9х — х^з= О; г) 5х⁴— 20х ²= О.

950. Решите уравнение:

б) х^з— 2х ²= О.

951. Докажите, что значения многочлена х^з— х при целых значениях х кратны числу 6.

952. Докажите, что разность квадратов двух последовательных нечётных чисел делится на 8.

953. Докажите, что если к произведению трёх последовательных целых чисел прибавить среднее из них, то полученная сумма будет равна кубу среднего числа.

954. Упростите выражение и найдите его значение при указанном значении переменной:

а) (6х — 1)(6х + 1) — (12х — 5)(Зх + 1) при х = 0,2;

б) (5 + 2х) ²— 2,5х(8х + 7) при х = —0,5.

955. Не выполняя построения, найдите координаты точек пересечения с осями координат графика функции:

а) у = 0,24х + 6; о 6х + 4,2; 6) 5х- 1,8; г) у = —х — 3,8.

956. Покажите, как примерно расположен в координатной плоско-

сти график функции:

а) у = —0,9х + 4;

10'

б) 2,3х; г)

д) у = —9,5;

е) у = 4 ².

1 89

Контрольные вопросы и задания

и выражения, не являюще-

в каком порядке, чтобы пред+ (х ²— 4) (х + 4) в виде мно-

Приведите пример целого выражения гося целым.

Какие действия надо выполнить и ставить целое выражение 4х (З — гочлена?

Какие способы разложения известны?

многочленов на множители вам

Для тех, кто хочет знать больше

39. Возведение двучлена в степень

Вам известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Так как разность а — Ь можно рассматривать как сумму а + (—b), то в каждом случае можно говорить не о двух формулах, а об одной — квадрате двучлена и кубе двучлена:

(а + = а ²+ 2ab + b ²

190

(а + = а ^з+ За ²Ь + ЗаЬ ²+ b³

Нетрудно получить формулы для возведения двучлена в четвёртую, пятую и т. д. степень. Получить их можно последовательно одну за другой, умножая многочлен, записанный в правой части предшествующей формулы, на а + Ь. Например:

(а ^з+ За ²Ь + ЗаЬ ²+ + Ь). Умножение выполним «в столбик»: а ^з+ 3a ²b + Зан + Ы

а ⁴+ За ³Ь + За ²Ь ²+ ab ³a ³b + За ²Ь ²+ ЗаЬ ³+ b ⁴а ⁴+ 4a ³b + 6a ²b ²+ 4ab³+ Ы.

Итак, (а + = а ⁴+ 4a ³b + 6a ²b ²+ 4ab ³+ b⁴.

Умножая правую часть этого равенства на а + Ь, получим формулу пятой степени двучлена:

а ⁴+ 4a ³b + 6a ²b ²+ 4ab³+ b⁴

а ⁵+ 4a ⁴b + 6a ³b ²+ 4a ²b ³+ ab⁴a ⁴b + 4a ³b ²+ 6a ²b ³+ 4ab ⁴+ b ⁵а ⁵+ 5a ⁴b + 10a ³b ²+ 10a ²b³+ 5ab⁴+ b ⁵

Значит,

(а + = а ⁵+ 5a ⁴b + 10a ⁸b ²+ 10a²b⁸+ 5ab ⁴+ Ь ⁵.

Для того чтобы заметить закономерность в формуле п-й степени двучлена а + Ь при различных значениях п, выпишем их, начиная с п = 1 и заканчивая п = 5.

(а + = а ²+ 2ab + b ²

(а + = а ^з+ За ²Ь + ЗаЬ ²+ Ы

(а + = а ⁴+ 4a³b + 6a ²b ²+ 4ab ³+ b⁴

(а + = а ⁵+ 5a⁴b + 10a ³b ²+ 10a ²b ³+ 5ab ⁴+ b ⁵

Рассматривая эти формулы, можно заметить, что в правой части каждой из них записан многочлен, содержащий п + 1 членов, где п — показатель степени двучлена.

Первый член многочлена равен а ^п, т. е. равен произведению а ^пи Ю. Далее при переходе к каждому последующему члену показатель степени а уменьшается на 1, а показатель степени Ь увеличивается на 1, т. е. сумма показателей степеней в каждом слагаемом равна п.

Сложнее обстоит дело с коэффициентами. Чтобы выявить закономерность в их образовании, выпишем по порядку в строку коэффициенты многочленов при п = 2, а затем при п = З:

1 '2 1

1 3 3 1

Во второй строке первый и последний коэффициенты равны 1. Нетрудно заметить, что второй коэффициент можно получить, сложив записанные над ним числа 1 и 2, третий — сложив записанные над ним числа 2 и 1.

По тому же правилу получаем строку для п = 4 из строки, записанной для п = З:

Аналогичным образом из строки

1 4 6 4 1

можно получить строку, в которой выписаны коэффициенты многочлена, полученного при возведении двучлена а + Ь в пятую степень:

1 4 6 4 1

1 5 10 10 5 1

Подмеченную закономерность нетрудно обосновать, если проанализировать приведённые ранее примеры на умножение «в столбик» многочлена а ^з+ За ²Ь + Зан + b ⁵на двучлен а + Ь и многочлена а⁴+ 4a ³b + 6a ²b ²+ 4ab ³+ b ⁴на двучлен а + Ь.

для тех, кто хочет знать больше

Если добавить строку для п = О (при а * О или Ь * О), то коэффициенты всех строк можно расположить в виде треугольника:

1 2 1

1 4 6 4 1

1 5 10 10 5 1

В нём «боковые стороны» состоят из единиц, а каждое из остальных чисел равно сумме двух чисел, записанных над ним. Этот треугольник называют треугольником Паскаля по имени известного французского учёного Блеза Паскаля (1623—1662) — математика, физика, философа и литератора, описавшего такой треугольник в своём знаменитом трактате «Об арифметическом треугольнике» .

Продолжая запись по подмеченному правилу, мы можем получить строку коэффициентов для п = 6, 7, 8 и т. д. в формуле (а + b) 'i = а ^п+ па ^в- + . .. + пар- ¹+ b 'i .

Существует способ, позволяющий сразу найти коэффициенты многочлена для заданного п. Однако этот способ связан с понятиями, которые вам пока неизвестны.

Отметим ещё одну интересную закономерность в треугольнике Паскаля. Сумма коэффициентов при п = О, п = 1, п = 2 и т. д. равна соответственно 2 ⁰2 ¹2 ²2 ³и т. д. Вообще в равенстве (а + = а ^п+ па ^П- ¹b + ... + паЬ ^П- ¹+ Ь ^п

сумма коэффициентов многочлена равна 2 'i . Убедиться в этом можно, подставив в это равенство а = 1 и Ь = 1.

Напишите строки треугольника Паскаля для п = 6; п = 7.

Используя треугольник Паскаля, напишите формулу для шестой степени двучлена а + Ь. Проверьте результат, умножив на а + Ь многочлен, равный (а + Ь) ⁵.

Напишите формулу;

а) седьмой степени двучлена; б) восьмой степени двучлена.

[Q] Используя формулу четвёртой степени двучлена, преобразуйте выражение:

а) (а ²+ 2b) ⁴;

192

Представьте в виде многочлена выражение: а) (а ²+ ЗЬ ³) ³; б) (1 — 2ху) ⁴.

Представьте в виде многочлена выражение:

а) (х + + (х — у) ⁶,

Выражение (1 + + (1 + + (1 + заменили тождественно равным многочленом. Найдите коэффициент члена многочлена, содержащего: а) у ²; б) у ^з.

Какой остаток получится при делении числа 147 ⁶на 145?

Докажите, что значение выражения:

а) 83 ⁴+ 65 кратно 81; б) 141 ¹⁰+ 88 кратно 139.

Дополнительные упражнения к главе V

К параграфу 12

Докажите тождество (а + Ь + = а ²+ 6 ²+ с ²+ 2ab + 2ас + 2bc.

967. Докажите, что значение выражения не зависит от х:

(х - + 19); 6) (х + + (8 - + 26).

968. Решите уравнение:

а) (3х + = 27х ²(х + 1) + 8х + 2;

6) 4х ²(2х + 9) = (2х + + 12(3х + 1).

969. Разложите на множители:

а) Н + + 25; в) 16х ²— 8х + 1;

б) с ²— 8с + 16; г) 4с ²+ 12с + 9;

д) х ⁴+ 2х ²у + у ²;

е) а ^б— 6a ³b ²+ 96 ⁴

970. Представьте в виде квадрата двучлена или в виде выражения, противоположного квадрату двучлена:

а) а ⁴— 8а ²+ 16;

ж) у — у ²— 0,25;

в) 10х — х ²— 25;	36
г) c ⁴d ²+ 1 — 2c ²d; д) а ^бЬ ²+ 12a ³b + 36; К параграфу 13 971. Вычислите:	и) -25 - 2п - 0,04п ²
а) 1005 • 995; в)	0,94 • 1,06;	6 д) 10— 7
6) 108 • 92; г)	1,09 • 0,91;	е) 99 Щ • 100?. 9
		к	V

Макарычев, 7 кл. 972. Представьте в виде многочлена:

а) 5у(у ²- + 3);

б) —8х(4х — х³) (4х + х³);

973. Упростите выражение:

10).

974. Докажите, что значение выражения не зависит от значения переменной:

а) (х -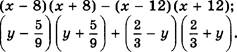

975. Преобразуйте в многочлен:

а) (х — + 2х(х — З);

4у(у - 2); е)

в) (а — 4)(а + 4) + (2а — 1) ²;

976. При каком значении х удвоенное произведение двучленов х + 2 и х — 2 меньше суммы их квадратов на 16?

977 • Представьте в виде многочлена:

г) (с — d + 8)(с — d — 8);

д) (р + 2q — — 2q — З);

в) (а — Ь — 5)(а — Ь + 5); е) (а — 3х + б)(а + 3х + 6).

978. Решите уравнение:

(х -

в) (2х — _ (7 - 2х) ²= 2; г) (5х — — з = 16х(х - 3).

979. Разложите на множители:

а) 1 — a ²b ²; в) 0,09х ⁶- 0,49$; д) 1—х

б) 4х ²у ⁴— 9; г) 1,210 ²- 0,366 ⁶; е) 0,01a ²b ⁴— 1

980. Найдите значение выражения:

57,5 ²-

72 ²—

38²- 17 ²39,5 ²- 3,5 ²17,5 ²- 9,5²а) б) в) ²- 3,5²131,5

981. Представьте в виде произведения:

г) 36 — b ⁴y ⁶; ж) 0,01х ¹⁶— 0,16;

б) д) 25p ⁴q ⁴— 1; з) - 1,21;

в) 0 ²х⁸— 81; е) —9 + 121m8n8; И) — т •

194

982. Разложите на множители:

а) (х — 16'

в) 25 - (3 - ху,

г) 81 — (а + 7)2; з) 4 - 25(х - 3) ².

983. Преобразуйте в произведение:

а) 16 — 9 (р + 3)2; в) 1 — 36 (Зу — 1) ²; 6) 9 - 25(4 - ху,

084. Докажите, что при любом натуральном п значение выражения:

а) (п + — (п — делится на 4;

б) (2n + — (2n — делится на 8;

в) (Зп + — (Зп — делится на 12;

г) (5n + — (2n — делится на 7.

985. Найдите значение выражения:

а) (За - 2b) ²- (2а — при а = 1,35 и Ь = —0,65;

б) (2у — + (у + 2с) ²при с = 1,2 и у = —1,4.

986. Разложите на множители:

а) 0,027х ³+ 1; в) d ³+ 0,0088;

6) - 0,001Х ³; Г) 125 - 0,064р ^З.

987. Представьте в виде произведения: а) 27 — У 12 б) —x15 + —1 в) 32а15 +82. г) 1 ⁹²х ¹⁸+ у ^з. 27 ' 64

988. Докажите, что значение выражения:

а) 41 ³+ 19 ³делится на 60; в) 66 ³+ 34 ³делится на 400;

б) 79 ³— 29 ³делится на 50; г) 54 ³— 24 ³делится на 1080.

989. Представьте в виде произведения:

д) 27а ^з— (а — Ь) ³; 6) (у - - 27; г) 8х ³+ (х — у) ³; е) 1000 + (Ь — 8)3.

К параграфу 14

990. Представьте в виде многочлена:

а) (а ²- + 2) - (20 - - 14); 6) (2 - + 26) + (1 + - 36).

991. Представьте в виде многочлена:

а) (х + 4)(х ²— 4х + 16); 6) (За + - 15а + 25). 992. Решите уравнение:

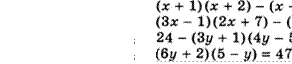- 7);

993. Дскажите, что функция, заданная формулой у = (2х - + 8х) - (1 - 4х) ²линейная. Принадлежит ли графику этой функции точка А (—1; 10)? точка В (О; 16)?

994. Найдите значение выражения:

а) (Зп — + 1) + (2n — — 1) — (Зп + 5) (п — 2) при п = —3,5;

б) (5у — 1)(2 — у) — (Зу + 4)(1 — у) + (2у + 6) (у — З) при у = 4.

995. Докажите, что значение выражения не зависит от значения переменной:

а) (а — З)(а ²— 8а + 5) — (а — 8)(а ²— За + 5);

б) (х ²— 3х + 2)(2х + 5) — (2х ²+ 7х + - 4).

Докажите тождество

(а2 + + cd) — ab(a2 + b2 — с2 — d2) = (ас + bd)(ad + bc).

[99( Докажите, что значение выражения

(Ь + с — 2а)(с — Ь) + (с + а — 2b)(a — с) — (а + Ь — 2с)(а — Ь) при любых значениях а, Ь и с равно О.

998. Упростите выражение:

6) (у

Упростите:

1 а) 2(а ²— 1) ² — —(а ²+ а 2

б) 4 (т ^з— — (Т ²— 6) (Т ²+ 6) — 9 (8 — т + Т ²)(1 — Т).

Представьте в виде многочлена

(а (а + 26) + — 2b) + — b ²) ²+ 4a ²b ²).

ДОКажите тождество:

а) (а + b) ²(a — Ь) — 2ab(b — а) — баб (а — Ь) = (а — Ь) ³;

б) (а + Ь) (а — + 2ab(a + Ь) — 2ab (—а — Ь) = (а + b) ³.

Докажите тождество

(а ²+ — a ²b ²+ 6 ⁴) — (а ^з— + Ы) = 26 ⁶

1003. Найдите значение выражения:

а) (у + 5)(у ²— 5у + 25) — у(у ²+ З) при у (х — 1)(х ²+ х + 1) при х

в) (2р — 1)(4р ²+ 2р + 1) —рф — 1)ф + 1) при р = 1,5.

В книге Леонарда Эйлера (XVIII в.) используется тождество (р ²+ + cs ²) = (pr + cqs) ²+ c(ps — qr) ².

Докажите его.

При каком значении а многочлен стандартного вида, ТОЖДеСТвенно равный произведению (х ²+ х — 1)(х — а), не содержит:

а) х²; б) х?

При каком значении Ь многочлен стандартного вида, тождественно равный произведению (х ²— 10х + 6) (2х + Ь):

а) не содержит х²,

б) имеет равные коэффициенты при х ³и при х?

1007. Представьте в виде произведения:

а) + 76³;	в) 5а ⁴+ 56 ⁴;	д) 1,2а ⁶+ 1,26 ⁶;
6) 20 ⁴- 26⁴;	г) 2,50 ⁶- 2,56 ⁶;	е) за ⁸- 36 ⁸.

Докажите, что число, равное разности 111 111 — 222, является квадратом натурального числа.

1009. Преобразуйте в произведение выражение:

а) 9с15 _ с13. б) х22 — —х20,1 в) а5 — 0,64а2•, г) у7 - 1-У5, 49

1010. Представьте в виде произведения:

а) 2х⁸— 12х⁴+ 18; в) a⁴b + 6a ²b ³+ 96 ⁵; 6) -20 - 8а^зь - 86 ²; г) 4х + 4ху ⁶+ ху ¹².

Разложите на МНОЭКИТеЛИ'.

а) 700 - 846 + 20аь - 246²; 6) 2168 - 6с - 38 + 426;

в) 12у — 9х ²+ 36 — 3х ²у;

г) зоа ^з- 18а ²Ь - 726 + 12Оа.

1012. Преобразуйте в произведение:

а) За ^з— ЗаЬ²+ a ²b — Ы;

б) 2х — а ²у — 2а ²х + у;

Решите уравнение:

а) х^з+ 3х ²- 4х - 12 = О;

б) 2m ³— т ²— 18m + 9 = О;

Решите уравнение:

а) х^з— 2х ²— х + 2 = О;

б) у^з— у ²= 16у — 16;

1015. Разложите на множители:

а) х ²— у²— 1,5(х — у);

в) Зр — 2с ³— 3с ³р + 2;

г) а ⁴- 24 + 8а - За ^З

в) у ^з— бу ²= 6 — у;

г) 20 ³+ за ²= 2а + З.

в) 2у ³— у ²— 32у + 16 = О; 4х ³— 3х ²= —

г) р ²— 168 — р — 4с;

б) х²

в) 4а ²— 6²— 2а + Ь; е)

1016. Представьте в виде произведения:

а) х ²(х + 2у) — х — 2у; в) а ^з— 5а ²— 4а + 20;

6) х²(2у - 5) - 8у + 20; г) х ^з— 4х ²— 9х + 36.

1017. Разложите на множители:

а) а2 — 62 + 2 (а + 02; в) 2 (х — + 3х2 _ Зу2;

б) 62 _ с2 — 10(b — с) ², г) 5а ²— 5 — 4 (а + 1) ².

Преобразуйте в произведение выражение:

а) а ²+ b ²— 2ab — 25; г) 6 ²— а ²— 12а - 36; 6) 36 - ь ²— с ²+ 2bc; д) 81а ²+ 6bc — 9b ²— 8;

в) 49 — 2ах — а ²— х², е) b ²c ²— 4bc — 6 ²— с ²+ 1

Разложите на множители:

а) х ^з+ у ^з+ 2ху(х + у); у ^з— 5х(х ²+ ху + у ²);

в) 2b ³+ а(а ²— 3b ²);

г) — 2р ²+ 2р — 1;

д) 8Ь ^З+ + зь + 1;

е) а ^з— 4а ²+ 20а — 125.

Представьте в виде произведения:

а) х ^з+ у ^з+ 2х ²— 2ху + 2у ²; в) а ⁴+ ab ³— а ^зь — Ы; 6) - Н + за ²+ заь + 36 ²; г) х ⁴+ х ³у — ху ³— у ⁴.

Докажите, что многочлен принимает лишь неотрицательные значения:

а) .r ²— 2ху + у ²+ а ²;

б) 4х ²+ а ²— 4х + 1;

в) 96 ²— 6b + 48 + 1;

г) а ²+ 2ab + 26 ²+ 26 + 1;

д) .r ²— 4ху + у ²+ х ²у ²+ 1;

е) х ²+ у ²+ 2х + бу + 10.

1022.; Может ли выражение:

а) а ²+ 16а + 64 принимать отрицательные значения;

б) —b ²— 25 + 10b принимать положительные значения;

в) —х ²+ 6х — 9 принимать неотрицательные значения;

г) (у + 10) ²— 0,1 принимать отрицательные значения;

д) 0,001 — (а + 100) ²принимать положительные значения?

1023. Делится ли на 5 при любом целом п выражение:

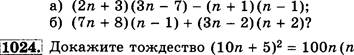+ 1) + 25.

Используя это тождество, сформулируйте правило возведения в квадрат натурального числа, оканчивающегося цифрой 5.

Найдите по этому правилу 25 ², 45 ², 75 ², 115 ²

198

УРАВНЕНИЙ

С уравнениями с одной переменной вы познакомились в младших классах, а об уравнениях с двумя переменными и их системах вы узнаете в этой главе. Вы познакомитесь с понятием линейного уравнения с двумя переменными, научитесь строить графики таких уравнений. Вы узнаете, что называется системой линейных уравнений с двумя переменными, научитесь решать такие системы графическим способом, способом подстановки и способом сложения. Теперь вы сможете решать текстовые задачи не только с помощью уравнений с одной переменной, но и с помощью систем уравнений с двумя переменными. Приобретённые вами умения составят основу для изучения в дальнейшем приёмов решения более сложных систем уравнений.

ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ

ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ

40. Линейное уравнение с двумя переменными

Пусть известно, что одно из двух чисел на 5 больше другого. Если первое число обозначить буквой х, а второе — буквой у, то соотношение между ними можно записать в виде равенства х — у = 5, содержащего две переменные. Такие равенства называют уравнениями с Двумя переменными или уравнениями с двумя неизвестНЫМИ.

Приведём другие примеры уравнений с двумя переменными: 5х + 2џ = 10, —7х + у = 5, х²+ у ²= 20, ху = 12. Из этих уравнений первые два имеют вид ах + бу = с, где а, Ь и с — числа. Такие уравнения называют линейными уравнениями с Двумя переменными.

О п р е д е л е н и е. Линейным уравнением с двумя переменными называется уравнение вида ах + by = с, где х и у — переменные, а, Ь и с — некоторые числа.

Уравнение х — у = 5 при х = 8, у = З обращается в верное равенство 8 — З = 5. Говорят, что пара значений переменных х = 8, у = З является решением этого уравнения.

О п р е д е л е н и е. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

Нетрудно проверить, что решениями уравнения х — у = 5 являются также пары: х = 105, у = 100; х = 4, у — 3,5, у = —1,5. Пары значений переменных записывают иногда короче. Например, перечисленные пары можно записать так: (105; 100), (4; —1), (3,5; —1,5). При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой — на втором. В записи решений уравнения с переменными х и у условимся на первом месте записывать значения х, а на втором — значения у.

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:

если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; 2 если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Рассмотрим уравнение

5х + 2у = 12. (1)

Воспользовавшись свойствами уравнений, выразим из этого уравнения одну переменную через другую, например у через х. Для этого перенесём слагаемое 5х в правую часть уравнения, изменив его знак: 2у = —5х + 12.

Разделим обе части этого уравнения на 2:

= —2,5х + 6. (2)

200	Глава Ш

Системы линейных уравнений

Уравнение (2) равносильно уравнению (1). Пользуясь формулой у = —2,5х + 6, можно найти сколько угодно решений уравнения (1). Для этого достаточно взять произвольное х и вычислить соответствующее ему значение у. Например: если х = 2, то у если х = 0,4, то у = -2,5 • 5.

Пары чисел (2; 1), (0,4; 5) — решения уравнения (1). Уравнение (1) имеет бесконечно много решений.

Иногда при решении задачи требуется найти все пары целых чисел или все пары натуральных чисел, удовлетворяющие уравнению с двумя переменными. В таких случаях говорят, что надо «решить уравнение в целых числах» или «решить уравнение в натуральных числах» .

Проблема решения уравнений в натуральных числах подробно рассматривалась в работах известного греческого математика Диофанта (III в.). В его трактате «Арифметика» приводятся остроумные способы решения в натуральных числах самых разнообразных уравнений. В связи с этим уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называют диофантовыми уравнениями.

Рассмотрим задачу, в которой надо найти натуральные решения уравнения с двумя переменными.

Зада ч а. Группу из 35 туристов решили расселить на теплоходе в трёхместные и четырёхместные каюты так, чтобы в каютах не оставалось свободных мест. Сколько трёхместных и сколько четырёхместных кают надо заказать?

Допустим, что надо заказать х трёхместных и у четырёхместных кают. Тогда

3х + = 35.

Требуется найти все пары натуральных значений переменных х и у, удовлетворяющие этому уравнению. Из уравнения 3х + 4у = 35 находим, что

35 - 3х

Подставляя в это равенство вместо х последовательно числа 1, 2, З и т. д., найдём, при каких натуральных значениях х соответствующие значения у являются натуральными числами: если х = 1, то у = 8; если х = 5, то у = 5; если х = 9, то у = 2.

Других пар натуральных чисел, удовлетворяющих уравнению 3х + 49' = 35, нет, так как при других натуральных значениях х соответствующее значение у является либо дробным положительным числом, либо отрицательным числом.

Значит, надо заказать соответственно трёхместных и четырёхместных кают либо 1 и 8, либо 5 и 5, либо 9 и 2. <Ј

ё и

1025. Является ли уравнение с двумя переменными линейным:

а) 3х - у = 17; в) 13х + бу = о;

б) х ²— 2у = 5; г) ху + 2х = 9?

1026. Является ли пара чисел х = 1— и у = 4— решением уравнения х + у = 6? Укажите ещё два решения этого уравнения.

1027. Пары значений переменных х и у указаны в таблице:

х	—5	—4	—3	-1		4	5
		З	4	-3	-5	-3

Какие из них являются решениями уравнения:

б) х + Зу = —5?

1028. Является ли решением уравнения 10х + у = 12 пара чисел (3; -20), 12), (0,1; 11), (1; 2), (2; 1)?

1029. Составьте какое-нибудь линейное уравнение с двумя переменными, решением которого служит пара чисел:

а) х = 2, у = 4,5;

1030. Из линейного уравнения 4х — Зу = 12 выразите:

а) у через х; б) х через у.

1031. Из уравнения 2u + = 4 выразите:

а) переменную v через и;

б) переменную и через и.

1032. Выразите из данного уравнения переменную у через х; используя полученную формулу, найдите три каких-либо решения этого уравнения:

а) 3х + 12; б) 5у — 2х = 1.

1033. а) Выразив из уравнения х — бу = 4 переменную х через у, найдите три каких-либо решения этого уравнения.

б) Выразив переменную у через переменную х, найдите три каких-либо решения уравнения 3х — у = 10.

1034. Среди решений уравнения х + 2у = 18 найдите такую пару, которая составлена из двух одинаковых чисел.

1035. Найдите значение коэффициента а в уравнении ах + 2у = 8, если известно, что пара х = 2, у = 1 является решением этого уравнения.

1036. Из двухрублёвых и пятирублёвых монет составлена сумма в 28 р. Сколько было взято двухрублёвых монет?

1037. Ученик купил тетради по 5 р. и карандаши по 7 р. Сколько тетрадей купил ученик, если известно, что за всю покупку он заплатил 44 р.?

1038. Хозяйка купила глубокие и мелкие тарелки, уплатив за покупку 320 р. Глубокая тарелка стоит 35 р., а мелкая тарелка стоит 30 р. Сколько глубоких и сколько мелких тарелок купила хозяйка?

1039. Мука расфасована в пакеты по З кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получить 20 кг муки?

1040. (Для работы в парах.) Купили тетради в линейку по 10 р. за каждую и тетради в клетку по 15 р. за каждую, затратив на всю покупку 320 р.

а) Выясните, можно ли при указанном условии купить одинаковое количество тетрадей в линейку и тетрадей в клетку.

б) Укажите все возможные пары, которые можно составить из числа тетрадей в линейку и числа тетрадей в клетку при указанном условии.

в) Найдите максимальное количество тетрадей, которые можно купить при указанном условии. г) Найдите минимальное количество тетрадей, которые можно купить при указанном условии, 1) Выполните совместно задания а) и б).

2) Распределите, кто выполняет задание в), а кто — задание г), и выполните их.

З) Проверьте друг у друга, верно ли выполнены задания, и исправьте ошибки, если они допущены.

1041. В результате перестановки цифр двузначного числа оно увеличилось на 54. Найдите это число.

1042. Найдите наименьшее натуральное число, которое при делении на 5 даёт остаток 1, а при делении на 6 — остаток 2.

; 1043. Найдите значение выражения:

а) 2с(с — 4) ²— с ²(2с — 10) при с = 0,2;

б) (а — 4b)(4b + а) при а = 1 2 Ь

в) Зр(1 + — 0,6р ²при р = —2.

1044. Разложите на множители:

а) 1 + а — а ²— а ^з, 6) 8 - + - 2b ²

5 и

41 . График линейного уравнения с двумя переменными

Каждая пара чисел, являющаяся решением уравнения с переменными х и у, изображается в координатной плоскости точкой, координатами которой служит эта пара чисел (абсциссой служит значение х, а ординатой — значение у). Все такие точки образуют график уравнения.

Графиком уравнения с двумя переменными называется мно! жество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

Выясним, что представляет собой график уравнения

Выразим переменную у через х: у = -1,5х + З.

Формулой у = —1,5х + З задаётся линейная функция, графиком которой служит прямая (рис. 74). Так как уравнения 3х + 2у = 6 и у = -1,5х + 3

равносильны, то эта прямая является и графиком уравнения 3х + 2у = 6.

С помощью таких же рассуждений можно показать, что графиком любого линейного уравнения с переменными х и у, в котором коэффициент при у не равен Рис. 74 нулю, является прямая.

Если в линейном уравнении коэффициент при у равен нулю, а коэффициент при х отличен от нуля, то графиком такого уравнения также является прямая. Рассмотрим, например, уравнение 2х + 12.

Его решениями служат пары чисел (х; у), в которых х = 6, а у — любое число, например (6; 2), (6; О), (6; —4,5). График уравнения состоит из всех точек, абсцисса которых равна 6, а ордината произвольному числу. Такие точки образуют прямую, проходящую через точку

Рис. 75 (6; О) и параллельную оси у (рис. 75).

204	Глава

Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.

Рассмотрим теперь случай, когда в линейном уравнении оба коэффициента при переменных равны нулю.

Уравнение ах + by = с,

в котором оба коэффициента при переменных равны нулю, имеет вид Ох + Оу = с. При с = О любая пара чисел является решением этого уравнения, а его графиком — вся координатная плоскость. При с * О уравнение не имеет решений и его график не содержит ни одной точки.

Приведём примеры построения графиков линейных уравнений.

Пример 1. Построим график уравнения 3х — 4у = 12.

В уравнении 3х — 4у = 12 коэффициенты при переменных отличны от нуля. Поэтому его графиком является прямая. Прямая определяется двумя точками. Найдём координаты двух какихлибо точек прямой:

если х = О, то у = —3; если х = 2, то у = —1,5.

Отметим точки (О; —3) и (2; —1,5) и проведём через них прямую (рис. 76). Эта прямая — график уравнения 3х — 4у = 12.

Пример 2. Построим график уравнения 0,5х = —1,5.

Это уравнение можно записать в виде 0,5х + Оу = —1,5. Его решениями служат пары чисел, в которых х = —3, у — произвольное число. Графиком уравнения является прямая, проходящая через точку (—3; О) и параллельная оси у (рис. 77).

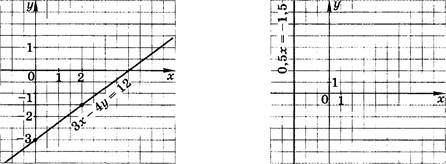
Рис. 76 Рис. 77

и их

Принадлежит ли графику уравнения 3х + 4у = 12 точка:

в) С (—6; —7,5),

1046. Какие из точек А (6; 1), В(—б; —5), С (О; —2), D(—1; З) принадлежат графику уравнения х — 2у = 4?

1047. Докажите, что графики уравнений 3х — у -5, -х + 10у = 21, 11х + 21 у = 31 проходят через точку Р (—1; 2) 1048. Постройте график уравнения:

а) 2х — у = 6; в) х + бу = О; д) 1,2х = —4,8;

б) 1,5х + 2у = З;

1049. Постройте график уравнения: в) 1,6х = 4,8;

1050. Постройте график уравнения:

в) 2 (х — у) + Зу = 4;

б) 3х = у + 4;

1051. На прямой, являющейся графиком уравнения 21х — бу = 100, взята точка, абсцисса которой равна З. Найдите ординату этой точки.

1052. Известно, что ордината некоторой точки прямой, являющейся графиком уравнения 12х — 5у = 132, равна О. Найдите абсциссу этой точки.

1053. (Для работы в парах.) Не выполняя построения, определите, в каких координатных четвертях расположен график уравнения: а) 12х - 8у = 25; 6) 6х + Зу = 11; в) 1,5х ²150; г) 0,2х = 43. 1) Обсудите друг с другом, в каких координатных углах при а О, Ь О может быть расположен график уравнения: ах = Ь; ау = Ь; ах + by = с.

2) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их.

З) Проверьте друг у друга, верно ли выполнены задания, и исправьте ошибки, если они допущены.

; 1054. Решите уравнение:

16 — х 18 — х х — 15

а) б)

2х + 1

+ 1 = 0.

8 12 2

51055. Найдите значение выражения:

а) а (а — 4) — (а + 4) ²при а = —1

б) (2а — 5) ²— 4 (а — 1)(3 + а) при а =

42. Системы линейных уравнений с двумя переменными

З ада ч а. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.

Обозначим первое число буквой х, а второе буквой у. По условию задачи сумма чисел равна 12, т. е. х+у= 12.

Так как разность чисел равна 2, то

Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений х + у = 12 и х — у = 2, т. е. найти общие решения этих уравнений. В таких случаях говорят, что требуется решить систему уравнений.

Систему уравнений принято записывать с помощью фигурной скобки. Составленную систему уравнений можно записать так:

Пара значений переменных х = 7, у = 5 служит решением каждого уравнения системы, так как оба равенства 7 + 5 = 12 и 7 — 5 = 2 являются верными. Такую пару называют решением системы.

О п р е д е л е н и е. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Решить систему уравнений — значит найти все её решения или доказать, что решений нет.

Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать графики уравнений.

Пусть требуется решить систему уравнений

2х+3џ = 5,

3х— у —

Построим в координатной плоскости графики уравнений системы. Графиком

первого уравнения является прямая АВ, а графиком второго — прямая CD (рис. 78).

208	Глава Ш

Координаты любой точки прямой АВ являются решением уравнения 2х + Зу = 5, а координаты любой точки прямой CD являются решением уравнения 3х — у Координаты точки пересечения прямых удовлетворяют как первому уравнению, так и второму, т. е. являются решением системы. Графики пересекаются в точке Рис. 78 К (—2; З). Значит, система имеет единственное решение: х —2, у З

Применённый нами способ решения системы уравнений называется графическим. Заметим, что графический способ обычно позволяет находить решения лишь приближённо.

Рассмотрим системы двух линейных уравнений с двумя переменными, в каждом из которых хотя бы один из коэффициентов при переменных отличен от нуля. Выясним, всегда ли такая система имеет решения и если имеет, то сколько. Графиками уравнений системы являются прямые. Если эти прямые пересекаются, то система имеет единственное решение; если прямые параллельны, то система не имеет решений; если прямые совпадают, то решений бесконечно много.

Пример 1. Выясним, сколько решений имеет система уравнений 11х + шу = 120, 6х+у = 18.

Рассмотрим, каково взаимное расположение графиков уравнений данной системы. Для этого выразим из каждого уравнения у через х, получим

= -1,1х + 12, у = —6х + 18.

Уравнениями у = —1,1х + 12 и у = —6х + 18 задаются линейные функции. Угловые коэффициенты прямых, являющихся графиками этих функций, различны.

Значит, эти прямые пересекаются и система имеет единственное решение.

П ри мер 2. Рассмотрим, сколько решений имеет система уравнений

2х + 5у = 16.

Из каждого уравнения системы выразим у через х: У - -0,4х+ 0,15, у = -0,4х+ 3,2.

Прямые, являющиеся графиками линейных функций у = —0,4х + 0,15 и у = -0 ,4х + 3,2,

параллельны, так как их угловые коэффициенты одинаковы, а точки пересечения с осью у различны.

Отсюда следует, что данная система уравнений не имеет решений.

Пример З. Выясним, сколько решений имеет система уравнений

5х + 2у = -18,

15х+ бу —

Выразив из каждого уравнения системы у через х, получим

{у = -2,5х- 9, у - -2,5х- 9.

Очевидно, что графики уравнений совпадают. Это означает, что любая пара чисел (хо; уо), в которой хо — произвольное число, а уо = —2,5х0 — 9, является решением системы. Система имеет бесконечно много решений.

1056. Является ли решением системы уравнений пара чисел: а) х = З, у = 1; б) х = 2, у = 2?

209

и их

.lQE Является ли пара чисел и = З, = — 1 решением системы уравнений:

а) 6)

Какие из пар (—3; 4), (—2; —6), (—4; З) являются решениями системы уравнений:

13х- у = О,

а)6)

5х— у = —4?

1059. Составьте какую-либо систему линейных уравнений с переменными х и у, решением которой служит пара:

1060. Решите графически систему линейных уравнений:

а)в)

б)г)

1061. Решите графически систему уравнений:

а) 6)

1062. Выясните, имеет ли система решения и сколько:

11 — 2у а)в)д)

— 22 — 4х,

б)г)

х + 4у = 10.

1063. в парах.) Имеет ли решения система уравнений и сколько: х = бу — 1,12х- зу = 5,

а) б)в)

2х- 10у = З;бу — 24х = —10?

1) Обсудите друг с другом, от чего зависит ответ на вопрос задачи.

2) Выполните совместно задание а),

З) Распределите, кто выполняет задание б), а кто — задание в), и выполните их.

4) Проверьте друг у друга правильность выполнения заданий и исправьте ошибки, если они допущены.

	Глава Ш

210

1064. Укажите какие-нибудь три решения системы уравнений:

1,5у + Х = -0,5,

а)б)

2х+Зу = -1.

1065. Решите уравнение:

3х- 1 х а)

4) 2 з 5

1066. Представьте в виде многочлена:

а) (58 — - 3) - 16; 6) 18т ^З-

! 1067. Разложите на множители:

³+ а ²— х ²а — х ², б) Ы + b2c _

дайте определение линейного Приведите пример.

Что называется решением Является ли пара значений уравнения 2х + у = 17?

Что является графиком уравнения х и у, где а * О или Ь * 0?

Что называется решением системы НЫМИ? Что значит решить систему Сколько решений может иметь с двумя переменными?

Контрольные вопросы и задания уравнения с двумя переменными.

уравнения с двумя переменными? переменных х = 7, у = З решением

ах + Ьу = с с переменными

уравнений с двумя переменуравнений?

система двух линейных уравнений

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

43. Способ подстановки

Рассмотрим способ решения систем линейных уравнений с двумя переменными, называемый способом подстановки. Начнём с примера.

Пример 1. Решим систему уравнений

(1)

Выразим из первого уравнения у через х: у = 7 — 3х.

Подставив во второе уравнение вместо у выражение 7 — 3х, получим систему

(2)

Нетрудно показать, что системы (1) и (2) имеют одни и те же решения.

В системе (2) второе уравнение содержит только одну переменную. Решим это уравнение:

-5х + 14 - 6х = з,

11х = -11,

Подставив в равенство у = 7 — 3х вместо х число 1, найдём соответствующее значение у:

Пара (1; 4) — решение системы (2), а значит, и системы (1).

Решение системы (1) мы свели к решению системы (2). При этом мы воспользовались тем, что системы (1) и (2) имеют одни и те же решения.

Системы уравнений с двумя переменРис. 79 ными, имеющие одни и те же решения, называются равносильными, Системы, не имеющие решений, также считают равносильными.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений системы (1) пересекаются в той же точке, что и графики уравнений системы (2), т. е. все три прямые пересекаются в одной точке (рис. 79).

Мы решили систему (1), используя способ подстановки. При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:

1) выражают из какого-нибудь уравнения системы одну переменную через другую;

2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;

З) решают получившееся уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

Пример 2. Решим систему уравнений

7х + бу = 6,

3х+ 4у 9.

CL'1CT€'M[Di ЛИН\ЭЙНЫХ

Выразим из второго уравнения х через у: 3х = 9 — 4у, х —

Подставим в первое уравнение вместо буквы х выражение з

9 — ау з

Решим полученное уравнение с переменной у:

63 - 28у + 18у = 18,

-10у = 9 — 4у

Подставим в уравнение х = вместо у число 4,5: з

⁴⁶, х = -3.

Ответ. х

1068. Решите систему уравнений:

а)6)

3х- и - 11 = 0

1069. Решите систему уравнений: у - х, 20,

а)в)д)

2х — 15у = -1;

25— х — 4у б)г)

2у ЗО

1070. Найдите решение системы уравнений:

2х+у = 12,

а)в)

2х- 21у = 2;

2х = у + 0,5, б)г)

3х- 5у = 12.

1071. Решите систему уравнений:

2u + 5v = О, 14 а)в)

-8u +15v = 7; 5u — 30 — 25

5р - 34 О, тор + 74 -2,

б)г)

2р- 22 = 5q.

1072. Решите систему уравнений:

5х+ бу —- -20,

а)в)

9у + 2х = 25;

3х+1 = 8у, 6)г)

11у - 3х = -11.

1073. Не выполняя построения, найдите координаты точки пересечения графиков уравнений:

а) + 23 и 8х- шу = 19; б) 11х — бу = 2 и —8х + 5у = З.

1074. Найдите координаты точки пересечения графиков уравнений, не выполняя построения:

а) 5х — 4у = 16 и х — 2у = 6; б) 20х — 15у = 100 и 3х — у = 6.

1075. Найдите решение системы уравнений:

а) б)

1076. Решите систему уравнений: бу + 8(х- Зу) = 7х - 12, -2(а - Ь) + 16 = + 7),

а)б)

+ — 9у) = 11 у + 46; ба — (а — 5)

1077. Найдите решение системы уравнений:

а)в)

6)г)

= -37;

1078. Решите систему уравнений:

а)в)

= 2,3, б)г)

= 1,2;

214	Глава Ш

Системы

1079. Упростите выражение:

а) (2х - зур + (2х + зу) ²•, в) 2

6) (2х + зу) ²- (2х - зу) ²•,

1080. Разложите на множители:

а) х ⁵+ 4а ²х ³— 4ах ⁴; 6) 40 ⁶— 12a ⁵b + 9a ⁴b ²

; 1081. Докажите, что все точки графика функции, заданной формулой у = х ²— 4х + 5, расположены в верхней полуплоскости.

44. Способ сложения

Рассмотрим ещё один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Пример 1. Решим систему уравнений

(1)

В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3х = 33. Заменим одно из уравнений системы (1), например первое, уравнением 3х = 33. Получим систему

3х = 33,

(2)

Система (2) равносильна системе (1).

Решим систему (2). Из уравнения 3х = 33 находим, что х = 11.

Подставив это значение х в уравнение х - зу = 38, получим уравнение с переменной у: 11 - зу = 38.

Решим это уравнение:

-зу = 27,

Пара (11; —9) — решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели её решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2х + Зу = —5 и х — Зу = 38 пересекаются в той же точке, что и графики уравнений 3х = 33 и х — Зу = = 38, т. е. все три прямые пересекаются в одной точке (рис. 80).

П р имер 2. Решим систему уравне-

Рис. 80 ний 5х+ 11 у = 8,

10х- 7у = 74.

Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены первого уравнения на —2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:

-10х- 22у = -16,

10х- = 74.

Теперь почленное сложение приводит к уравнению с одной переменной —29у 58. Из этого уравнения находим, что у — Подставив во второе уравнение вместо у число —2, найдём значение х:

10х - 7 . = 74, = 60, х = 6.

Ответ. х = 6, у = -2.

3х- 5у = 93, Пример З. Решим систему уравнений

5х- 4у = 103.

Подберём множители к уравнениям системы так, чтобы после умножения на них коэффициенты при у стали противоположными числами. Умножив первое уравнение системы на —4, а второе на 5, получим

-12х+ 20џ = -372,

25х — 20у = 515.

Отсюда найдём, что 13х = 143, х = 11. Подставив значение х в уравнение 5х — 4у = 103, найдём, что у - — -12. Ответ. х = 11, у -12.

Системы

Мы рассмотрели примеры решения систем способом сложения. При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из перемен ных стали противоположными числами;

2) складывают почленно левые и правые части уравнений системы;

З) решают получившееся уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

Заметим, что если коэффициенты при одной из переменных являются противоположными числами, то решение сразу начинают с почленного сложения уравнений.

1082. Решите систему уравнений:

2х+ 11у = 15, 4х- = ЗО а)в)

10х- 11у = 9; 4х — 5у —- 90;

8х- 17у 4, 13х- 8у = 28,

6)г)

—8х+ 15у = 4; 11х— 8у = 24

1083. Найдите решение системы уравнений: 3х+ 2у 5,

а)в)

4у = -13, б)г)

9х - 2у - -20.

1084. Решите систему уравнений:

40х+ зу = 10, ЗЗа + = 10, 10х- 9у = 8,

а)в)д)

20х- = 5;21у + 15х = 0,5;

5х — 2у = 1, 13х- 12у = 14, 9у + 82 = —2,

б)г)

15х — Зу — 11х- 4 = 18у; 52 —

1085. Решите систему уравнений:

12х- = 2, 6х = 25у + 1,

а)в)

4х — 5у — 6; 5х— 1 бу — —4;

7u+ 2v - 1,+ 70 = 90, б)г)

- 6b = 20.

линейных уравнений

1086. Найдите решение системы уравнений:

0,75х+ 20у = 95,

а)в) 0,32х- 25у = 7; о,5и - 0,6v = о,

6)г)

о,4и + 1,70 = 10,9;

1087. Составьте уравнение вида у = Кх + Ь, график которого прохо-

дит через точки:

а) М(5; 5) и N(-10; -19); в) А (8; -1) и щ-4•, 17);

г) щ-19; 31) и D(1; -9).

1088. График линейной функции пересекает оси координат в точках (—5; 0) и (О; 11). Задайте эту функцию формулой.





								х

1089. Прямая у = Кх + Ь проходит через точки А (—1; З) и Щ 2; —1). Напишите уравнение этой прямой.

1090. График линейной функции пересекает

ось х в точке с абсциссой 4, а ось у в точке с ординатой 11. Задайте эту функцию формулой.

1091. Задайте формулой линейную функцию, график которой изображён на рисунке 81.

Рис. 81 1092. Решите систему уравнений:

5(х + 2у) — З = х + 5, - Зу)- з = -3х + 0,5,

а) 6)

у + 4(х — Зу) 50; з (х + бу) 9у + 19.

1093. Найдите решение системы уравнений:

в)

г)

в)

г)

1095. Найдите решение системы уравнений:

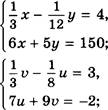в)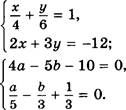

1096. Имеет ли решения система и сколько:

а)б)

-21?

^в1097. Разложите на множители:

а) 15а ²— 15b ²; в) 100³+ 10“; 6) 298 + 298 + 58ab; г) 18а ^з- 18“;

1098. Упростите выражение:

д) 47а⁶- 478;

е) 51а⁶+ 51b ⁶.

а) 2х(8х — 1)6) 4(3у - - 18у(2у - 1).

45. Решение задач с помощью систем уравнений

При решении задач с помощью систем уравнений поступают следующим образом:

1) обозначают некоторые неизвестные числа буквами и, используя условие задачи, составляют систему уравнений; 2) решают эту систему;

З) истолковывают результат в соответствии с условием задачи.

Задача 1. Масса 15 кирпичей и 5 шлакоблоков равна 64 кг. Какова масса одного кирпича и одного шлакоблока, если 5 кирпичей тяжелее 2 шлакоблоков на З кг?

Пусть масса кирпича х кг, а шлакоблока у кг. Тогда масса 15 кирпичей и 5 шлакоблоков будет 15х + 5у кг. По условию задачи она равна 64 кг, поэтому 15х + 5у = 64.

Известно, что 5 кирпичей тяжелее 2 шлакоблоков на З кг. Значит,

линейных уравнений

Чтобы ответить на вопрос задачи, надо найти такие значения х и у, которые удовлетворяют как первому, так и второму уравнению, т. е. удовлетворяют системе

Решив эту систему, получим, что х = 2,6, у = 5.

Ответ. Масса кирпича 2,6 кг, а шлакоблока 5 кг.

Задача 2. Можно ли разменять сторублёвую купюру пятирублёвыми и однорублёвыми монетами так, чтобы всех монет было 30? Допустим, что следует взять х пятирублёвых и у однорублёвых монет. По условию х + у = 30. Так как с помощью этих монет нужно разменять 100 р., то должно выполняться равенство 5х + у = 100. Получили систему уравнений

Решив её, найдём, что х = 17— , у = 12— .

По смыслу задачи х и у должны быть натуральными числами, а мы получили дробные числа.

Отв е т. Разменять сторублёвую купюру указанным способом невозможно.

1099. В фермерском хозяйстве под гречиху и просо отведено 19 га, причём гречиха занимает на 5 га больше, чем просо. Сколько гектаров отведено под каждую из этих культур?

1100. Техническое перевооружение цеха позволило выпустить в феврале на 165 изделий больше, чем в январе. Сколько изделий было выпущено в январе и сколько в феврале, если известно, что за эти месяцы цех выпустил 1315 изделий?

1101. В мастерской «Автосервис» отремонтировали 22 легковых и грузовых автомобиля. Среди них легковых было на 8 меньше, чем грузовых. Сколько грузовых автомобилей отремонтировали в мастерской?

1102. На теннисном корте для игры пар теннисистов выделяется площадка прямоугольной формы. Найдите длину и ширину площадки, если известно, что длина больше ширины на 12,8 м, а периметр прямоугольника равен 69,48 м.

220	Глава Ш

1103. Основание равнобедренного треугольника на 7 см больше его боковой стороны. Найдите боковую сторону треугольника, если его периметр равен 43 см

1104. Старинная задача. Ослица и мул шли вместе, нагруженные равными по весу мешками. Ослица жаловалась на тяжесть ноши. «Что ты жалуешься, — сказал мул, — если ты дашь мне твой мешок, моя ноша станет вдвое больше твоей, а если я тебе дам один мешок, то наши грузы сравняются». Сколько мешков нёс каждый?

1105. Старинная заДача. Если А получит от В 100 рупий, то станет вдвое его богаче, а если А даст В 10 рупий, то В станет вшестеро богаче. Сколько денег у каждого?

1106. Сколько лет брату и сколько лет сестре, если 2 года назад брат был старше сестры в 2 раза, а 8 лет назад — в 5 раз?

1107. Два автомата изготавливают детали. Число деталей, изготовленных первым автоматом за З ч и вторым за 2 ч, составляет 720 штук. Четвёртая часть деталей, изготовленных обоими автоматами за 2 ч, составила 150 штук. Сколько деталей изготовлял каждый автомат за час?

1108. За 4 ч езды на автомашине и 7 ч езды на поезде туристы проехали 640 км. Какова скорость поезда, если она на 5 км/ч больше скорости автомашины?

1109. Теплоход проходит за З ч по течению и 2 ч против течения

240 км. Этот же теплоход за З ч против течения проходит на 35 км больше, чем за 2 ч по течению. Найдите скорость теплохода против течения и его скорость по течению.

1110. Из пунктов А и В, расстояние между которыми равно 280 км, выходят одновременно два автомобиля. Если автомобили будут двигаться навстречу друг другу, то встреча произойдёт через 2 ч. Если же они будут двигаться в одном направлении, то автомобиль, вышедший из А, догонит автомобиль, вышедший из В, через 14 ч. Какова скорость каждого автомобиля?

между которыми 38 км, и встретились через 4 ч. С какой скоростью шёл каждый турист, если известно, что первый прошёл до встречи на 2 км больше второго?

1112. Моторная лодка путь по течению от одной пристани до другой проходит за 4 ч, а обратный путь — за 5 ч. Какова скорость лодки в стоячей воде, если 70 км по течению она проходит за 3,5 ч?

1113. За З ч по течению и 4 ч против течения теплоход проходит 380 км. За 1 ч по течению и 30 мин против течения теплоход проходит 85 км. Найдите собственную скорость теплохода и скорость течения.

линейных •џравнений

1114. На двух полках 55 книг. Если переставить со второй полки половину книг на первую, то на первой станет в 4 раза больше книг, чем останется на второй. Сколько книг на каждой полке?

1115. Старинная заДача. На левой чаше весов, находящихся в равновесии, лежат 9 одинаковых слитков золота, а на правой 11 одинаковых слитков серебра. Если поменять местами один слиток золота со слитком серебра, то левая чаша окажется на 13 г легче правой. Сколько весит один слиток золота и один слиток серебра?

1116. Масса 4,5 см ^зжелеза и 8 см ^змеди равна 101,5 г. Масса З см ^зжелеза больше массы 2 см ^змеди на 6,8 г. Найдите плотность железа и плотность меди.

1117. Под озимыми культурами было занято на 480 га больше, чем под яровыми. После того как убрали 80 ⁰/0 озимых и 25 ⁰/0 яровых культур, площадь, оставшаяся под озимыми, оказалась на ЗОО га меньше, чем площадь под яровыми. Какая площадь была отведена под яровые и какая под озимые культуры?

1118. Две бригады должны были по плану изготовить за месяц 680 деталей. Первая бригада перевыполнила месячное задание на 20 ⁰/0 , а вторая — на 15 ⁰/0 , и поэтому обеими бригадами было изготовлено сверх плана 118 деталей. Сколько деталей должна была изготовить по плану каждая бригада за месяц?

[1119.; Имеется молоко 5 ⁰/0 жирности и 1 % жирности. Сколько молока каждого вида надо взять, чтобы получить З л молока, жирность которого составляет 3,2 % ?

[1120., Имеющиеся 45 ООО р. клиент банка разделил на две части. Одну из них он положил на вклад «Депозитный», доход по которому составлял 9 ⁰/0 в год, но нельзя было снимать деньги в течение года. Другую часть он положил на вклад «До востребования», доход по которому составлял 1 % в год, однако в любое время можно было взять деньги полностью или частично. В результате общий доход, полученный клиентом через год, составил 3410 р. Сколько денег положил клиент на вклад «Депозитный» и сколько на вклад «До востребования»?

1121.3 Из 10-процентного и 15-процентного растворов соляной кислоты требуется составить 80 г раствора, концентрация которого равна 12 ⁰/0 . Сколько граммов каждого раствора надо взять?

Смешав кислоту 70-процентной и 48-процентной концентрации, получили 660 г кислоты 60-процентной концентрации. Сколько было взято кислоты каждого вида?

Глава Ш

222

1123. (ЗаДача-исслеДование.) На сколько надо уменьшить число 100, чтобы при делении полученной разности как на 5, так и на 7 остаток был равен 1 и при этом первое частное было на 2 больше второго?

1) Обсудите, какие обозначения удобно ввести для решения

задачи.

2) Составьте систему уравнений и решите её.

З) Проверьте правильность полученного ответа.

1124. Разложите на множители:

а) 0,064m ³+ 1; 6) 0,027х3 - уз; 6

1125. Докажите тождество

(х ^з— у^з+ 2х³у ³= х2у2).

1126. В каких координатных четвертях расположен график уравнения:

а) 2х + 5у = 12;

1127. Докажите, что все точки графика функции, заданной формулой у = —х ²— 6х — 11, расположены в нижней полуплоскости.

Контрольные вопросы и задания

Объясните на примере, как решают систему двух линейных уравнений с двумя переменными способом подстановки.

Объясните на примере, как решают систему двух линейных уравнений с двумя переменными способом сложения.

Для тех, кто хочет знать больше

46, Линейные неравенства с двумя переменными и их системы

Неравенство у > 0,5х + 2 при х = 6, у = 10 обращается в верное неравенство 10 > 0,5 • 6 + 2. Говорят, что пара значений переменных х = 6, у = 10 является решением этого неравенства.

О п р е д е л е н и е. Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное числовое неравенство.

для тех, кто хочет знать больше

Нетрудно проверить, что решениями неравенства у > 0,5х + 2

являются также пары х = О, у = 5; х = —8, у = —1. Каждое решение неравенства у > 0,5х + 2 можно изобразить точкой на координатной плоскости.

Выясним, какое множество точек задаёт на координатной плоскости рассматриваемое неравенство.

Множество точек, координаты которых удовлетворяют уравнению у = 0,5х + 2, представляет собой прямую (рис. 82). Если точка плоскости лежит выше, чем точка этой прямой, находящаяся с ней на одной вертикали (см. рис. 82), то её ордината больше ординаты соответствующей точки прямой и потому координаты этой точки удовлетворяют неравенству у > 0,5х + 2.

Вообще координаты любой точки полуплоскости, расположенной выше прямой у = 0,5х + 2, удовлетворяют неравенству у > 0,5х + 2, а координаты других точек плоскости этому неравенству не удовлетворяют.

Таким образом, неравенство у > 0,5х + 2 задаёт полуплоскость, расположенную выше прямой у = 0,5х + 2. На рисунке 82 эта полуплоскость показана цветом. Граничная прямая, не принадлежащая этой полуплоскости, проведена пунктиром.

Пример 1. Покажем в координатной плоскости множество точек, которое задаёт неравенство х 4.

Проведём прямую х = 4 (рис. 83). Абсцисса любой точки, принадлежащей этой прямой или расположенной правее её, равна 4 или больше 4. Значит, неравенство х 4 задаёт на координатной плоскости прямую х = 4 и полуплоскость, расположенную правее прямой х = 4. Эта полуплоскость показана на рисунке цветом. Граничная прямая принадлежит этой полуплоскости.

-2

—4

-4

-2

—6

Рис. 82 Рис. 83

224	Глава

6 х

Пример 2. Выясним, какое множество точек задаёт на координатной плоскости система неравенств у 0,4х — 2, у < 0,4х + З.

Построим в координатной плоскости прямые, являющиеся графиками уравнений у = 0,4х — 2 и у = 0,4х + З.

Так как угловые коэффициенты прямых равны, то эти прямые Рис. 84 параллельны.

Первое нестрогое неравенство задаёт прямую у = 0,4х — 2 и полуплоскость, расположенную выше этой прямой, а второе — прямую у = 0,4х + З и полуплоскость, расположенную ниже этой прямой. Рассматриваемая система неравенств задаёт общую часть этих множеств.

Эта общая часть представляет собой полосу, ограниченную прямыми у = 0,4х — 2 и у = 0,4х + З (рис. 84).

1 1128. Постройте прямую у = — х. Покажите штриховкой множество З точек координатной плоскости, координаты которых удовлеТВОРЯЮТ неравенству: 1 1

З З

1129. Покажите штриховкой множество точек координатной плоскости, которое задаёт неравенство:

1130. Изобразите множество точек, которое задаёт на координатной плоскости неравенство:

а) у э х + 1; 6) 0,2х + З.

1131.1 Задайте неравенством полуплоскость, расположенную выше прямой:

а) у = х — 1,3;

1132. Является ли пара чисел х = —3, у = 4 решением системы неравенств:

а)6)

-15?

225

для тех, кто хочет знать больше

Макарычев, 7 кл.

Изобразите на координатной плоскости множество точек, которое задаёт система неравенств:

а) б) в)

Какую фигуру на координатной плоскости задаёт система неравенств:

а) 6)

Изобразите на координатной плоскости фигуру, которую задаёт система неравенств

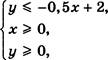
и найдите её площадь.

[$*l Укажите какие-либо значения К и Ь, при которых система неравенств

задаёт на координатной плоскости: а) полосу; б) угол.

—•у:рапения к главе И

К параграфу 15

1137. Является ли решением уравнения х ²— 2у = 7 пара значений переменных х и у:

6) (-4; -11,5); г) (1,2; -2,78)?

1138. Составьте уравнение с переменными и и и, решением которого служит пара чисел вида (и; и):

в) (0,6; -0,8); г) (-1,4; -3,6).

Докажите, что если в уравнении ах + by = 81 коэффициенты а и Ь — целые числа, то пара чисел (15; 40) не может быть решением этого уравнения. 1140. Известно, что:

а) пара значений переменных х = 5, у = 7 является решением уравнения ах — 2у = 1. Найдите коэффициент а;

б) пара значений переменных х = —3, у = 8 является решением уравнения 5х + by = 17. Найдите коэффициент Ь.

226

1141. Найдите все пары натуральных чисел, которые являются решением уравнения: а) х + у = 11; б) ху = 18.

Найдите все пары простых чисел, которые являются решениями уравнения а + Ь = 42.

Трёхзначное число начинается с цифры 9. Если эту цифру переставить на последнее место, то получится трёхзначное число, которое меньше данного на 576. Найдите данное трёхзначное число.

Трёхзначное число оканчивается цифрой 4. Если эту цифру поставить на первое место, то новое число будет на 7 меньше удвоенного данного числа. Найдите данное число.

К двузначному числу приписали слева и справа по 1. Получившееся четырёхзначное число оказалось в 21 раз больше первоначального. Найдите двузначное число.

Пересекает ли график уравнения у — х ²= 9: а) ось х; б) ось у? При положительном ответе укажите координаты точек пересечения.

1147. Графику уравнения х — ху = 46 принадлежит точка с ординатой —1,3. Найдите абсциссу этой точки.

1148. График уравнения 8х — 5у = 14 проходит через точку с абсциссой 1,2. Найдите ординату этой точки.

1149. Докажите, что графику уравнения 3х + 2у = —4 не принадлежит ни одна точка, у которой обе координаты положительны.

Докажите, что графику уравнения 6х — 12у = 5 не принадлежит ни одна точка с целочисленными координатами.

1151. Постройте график уравнения:

а) З(х — 2у) — 2 (х — 4у) = 4;

б) 2 (0,5х — 1,2у) —(О,6у + х) = 6;

в) - 0,2х) - - 0,6х) = 0,6.

1152. В линейном уравнении ах — у = 4 подберите коэффициент а так, чтобы график этого уравнения проходил через точку М(З; 5). Постройте график этого уравнения.

1153. Постройте прямую, которая является графиком уравнения у — 2,5х = с, если известно, что она проходит через точку

ПОСТР0йте график уравнения:

в) (х + 4)(у + 5) = О;

б) (х + 8)(у — 1) = О;

227

Не выполняя построения, найдите координаты точки пересечения графика уравнения (х + 2) (у + З) = О с осью х; с осью у. 1156. Постройте график уравнения:

а) y = lx ;

1157. Является ли решением системы уравнений

пара чисел:

1158. Докажите, что прямые х + у = 5, 2х — у = 16 и х + 2у З пересекаются в одной точке. Каковы координаты этой точки?

При каком значении а прямые 5х — 2у = З и х + у = а пересекаются в точке, принадлежащей оси у?

[Пф] При каком значении Ь прямые bx + Зу = 10 и х — 2у = 4 пересекаются в точке, принадлежащей оси х?

При каком значении К прямая у = Кх — 4 проходит через точку пересечения прямых у = 2х — 5 и у = —х + 1? 1162. Решите графически систему уравнений:

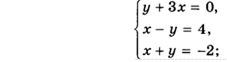
1163. Имеет ли система решения и если имеет, то сколько:

2х+ 5у = 17, 0,2х- 5у = 11, а)в)

4х- шу = 45; —х + 25у = —55;

3х+ —у = 10,

6) 5 15 г)

6х- 2у = 35;

1164. (Для работы в парах.) Подберите какое-либо линейное уравнение с двумя переменными, которое вместе с уравнением 10х + 5у = 1 составило бы систему: а) имеющую одно решение; б) имеющую бесконечно много решений; в) не имеющую решений.

1) Выполните совместно задание а) и решите составленную систему.

2) Распределите, кто выполняет задание б), а кто — задание в), и выполните их.

З) Проверьте друг у друга правильность выполнения заданий и исправьте ошибки, если они допущены.

228	Глава Ш

1165. Укажите какое-либо значение К, при котором система

имеет единственное решение.

1166. При каком значении с система уравнений 3х-у = 10,

имеет бесконечно много решений?

1167. При каких значениях с система уравнений

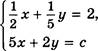
не имеет решений?

К параграфу 16

1168. Решите систему уравнений:

25х - 18у = 75, 13х — 15у —

а)г)

5х — 4у = 5;

35х = зу + 5, 7х + 4у = 74, б)д)

49Х = + 9; 3х + 2у = 32;

8у - 5z = 23, пи + 15v = 1,9,

в)

—3u + 5v = 1,3.

1169. Найдите решение системы уравнений: б(х+у) = 8 + 2х — Зу, а)

5(у — х) = 5+ 3х + 2у;

-2(2х + 1) + = - 2) - бх,

б)

11,5- - х) = 2у - (5 - х);

4(2х- у + 3) - 2у + 3) = 48,

в)

3(3х- 4у 2у - 9) = 48;

84+ - Зу) = 36х - + 17),

г)

10(х — у) = Зу + 4(1 — х).

229

1170. Решите систему уравнений:

б)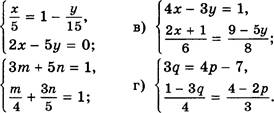

1171. Найдите решение системы:

2 = 6v,

а)

— 4u.

1172. Решите систему уравнений:

а)

б)

Имеет ли решения система уравнений: 5х— 4у = 1,11х+ Зу = 1,

а) 3х+1 = 13, 6) 2х+у = З,

7х — 5у = 1;5х + 2у = 4?

Проходят ли прямые 2х + Зу = 20, 3х — 5у = 11 и х + у = 9 через одну и ту же точку?

1175. Задайте формулой линейную функцию, график которой проходит через точки:

1176. (Для работы в парах.) Напишите уравнение вида у = Кх + Ь, график которого проходит через точки: а) М (—1; 1) и Р (4; 4); 6) А (-3; 3) и ЩЗ•, -3).

1) Обсудите друг с другом ход решения задачи.

2) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

З) Проверьте друг у друга, правильно ли составлены уравнения, построив соответствующие графики.

1177. Автомобиль проделал путь за 8 ч. Сначала он шёл со скоростью 40 км/ч, а затем со скоростью 60 км/ч. Весь этот путь он мог бы пройти за то же время, если бы шёл со скоростью 45 км/ч. Сколько часов шёл автомобиль со скоростью 40 км/ч и сколько со скоростью 60 км/ч?

230	Глава Ш

1178. Велосипедист ехал от пункта А до пункта В со скоростью 10 км/ч, а от пункта В до пункта С со скоростью 15 км/ч. На весь путь он затратил 5 ч. Тот же путь за то же время он мог бы проехать со скоростью 12 км/ч. Сколько часов затратил велосипедист на путь от А до В и сколько на путь от В до С?

1179. В первый день засеяли — первого поля и — второго, что составило 340 га. Во второй засеяли — оставшейся части первого

поля, что на 60 га меньше половины оставшейся части второго поля. Найдите площадь каждого поля.

1180. Если каждую сторону прямоугольника увеличить на З см, то его площадь увеличится на 90 см ². Если же длину прямоугольника увеличить на 5 см, а ширину уменьшить на 2 см, то его площадь увеличится на 20 см ². Найдите стороны прямоугольника.

Написали два числа. Если первое число увеличить на 30 ⁰/0 , а второе уменьшить на 10 ⁰/0, то их сумма увеличится на 6. Если же первое число уменьшить на 10 ⁰/0 , а второе — на 20 ⁰/0 , то их сумма уменьшится на 16. Какие числа были написаны?

В магазине находилось два мешка с рисом одинаковой массы и один мешок с пшеном. Масса всех трёх мешков составляла 160 кг. После того как из каждого мешка с рисом продали 20 ⁰/0 риса, а из мешка с пшеном — 25 ⁰/0 пшена, масса крупы в мешках составила 125 кг. Сколько килограммов риса и пшена было в каждом мешке первоначально?

За 8 дней работы на первом станке и 5 дней работы на втором было изготовлено 235 деталей. В результате усовершенствования производительность первого станка возросла на 15 ⁰/0 а второго — на 20 ⁰/0 . Теперь за 2 дня работы на первом станке и З дня на втором можно изготовить 100 деталей. Сколько деталей в день изготовляли раньше на каждом станке?

231

ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ

[$3842] Найдите все натуральные значения а, при которых корень уравнения (а — 1) х = 12 является натуральным числом.

Решите уравнение:

в) 4 — х! = 1,5;

6) х + 21 = 9; г) 7,3.

В шестизначном числе первая цифра совпадает с четвёртой, вторая — с пятой и третья — с шестой. Докажите, что это число кратно 7, 11, 13.

В двух бочках было воды поровну. Количество воды в первой бочке сначала уменьшилось на 10 ⁰/0 , затем увеличилось на 10 ⁰/0 , а во второй бочке сначала увеличилось на 10 ⁰/0 , а затем уменьшилось на 10 ⁰/0. В какой бочке стало больше воды?

Свежие грибы содержат 9094 воды, а сухие грибы воды. Сколько получится сухих грибов из 11 кг свежих?

Три ящика наполнены орехами. Во втором ящике на 10 ⁰/0 орехов больше, чем в первом, и на 30 ⁰/0 больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?

232

Задачи повышенной трудности

1190. Докажите, что сумма 1 ³+ 2 ³+ + 99 ³делится на 100.

2191.; Число а составляет 80 ⁰/0 числа Ь, а число с составляет 140 ⁰/0 числа Ь. Найдите числа а, Ь и с, если число с больше а на 72.

Д192.л Число а составляет 75 ⁰/0 числа Ь и 40 ⁰/0 числа с. Число с на 42 больше числа Ь. Найдите числа а и Ь.

1193.; Какое двузначное число в 4 раза больше суммы его цифр? [1194.] Делится ли число 111...1 на 81?

81 раз

11952] Докажите, что остаток от деления простого числа на 30 есть простое число или единица.

21196.] К некоторому двузначному числу слева и справа приписали по единице. В результате получили число, в 23 раза большее первоначального. Найдите это двузначное число.

^E1i97.l В двузначном числе зачеркнули одну цифру. Получилось число, которое в 31 раз меньше первоначального. Какую цифру и в каком числе зачеркнули?

Первая цифра трёхзначного числа 8. Если эту цифру переставить на последнее место, то число увеличится на 18. Найдите первоначальное число.

1199.] Постройте график уравнения:

б) х ²+ ху = О.

Постройте график уравнения: а) у + = х; б) у = xlyl.

1201., Постройте график функции: а) у = — З; б) у = 4 — 1 х

11202. Найдите наименьшее натуральное число, которое после умножения на 2 станет квадратом, а после умножения на З — кубом натурального числа.

Д2ОЗ. Докажите, что значение выражения 96 ⁷— 22 ⁵— 48 ⁶кратно 10. 1204. В координатной плоскости (рис. 85) отмечена точка М (х; у). Отметьте в этой координатной плоскости точки А (2х; 2у),






						х

12054 Что больше:

1010+ 1 1011+ 1 или 9

1011+ 1 10¹²+ 1

Д206.ј Представьте выражение 2х ²+ 2у ²в виде суммы двух квадратов.

Если х * О или у * О, то значение выражения 15х ²— 18ху + 15у ²положительно. Докажите это. Рис. 85

Задачи повышенной трудности

Разложите на множители многочлен:

а) х⁸+ х ⁴— 2; б) а ⁵— в) п ⁴+ 4; г) п ⁴+ п ²+ 1.

Докажите, что р ²— 1 кратно 24, если р — простое число, большее З.

Докажите, что разность между кубами двух последовательных натуральных чисел при делении на 6 даёт остаток 1.

Докажите, что сумма квадратов пяти последовательных натуральных чисел не может быть квадратом натурального числа.

Докажите, что разность между квадратом натурального числа, не кратного З, и числом 1 кратна З.

У Простите выражение

Докажите, что уравнение х ²— у ²= 30 не имеет целых решений.

[$2353 Докажите, что не существует целых коэффициентов а, Ь, с и d, таких, что значение многочлена ах ^з+ bx ²+ сх + d равно 1 при х = 19 и равно 2 при х = 62.

Докажите, что если у есть среднее арифметическое х и г, то .r ⁴+ 2х ³2 — 2хг ³— 2 ⁴— 4х ²у ²+ 4у ²г ²= О.

Найдите все простые числа р и q, для которых р ²— 2q ²= 1

При каких значениях а, Ь, с и d является тождеством равенство

5х ³- 32х ²+ 75х - 71 = - + - + - 2) + С?

Представьте многочлен 3х ³+ 7х ²+ 9х + 6 в виде многочлена ау ^з+ by ²+ су + d, где у = х + 1.

[2*] При каких натуральных значениях х и у верно равенство

Решите систему уравнений:

lx+y = -3, х— у + 2г = 1,

2х— у +г = —1.

Найдите трёхзначное число, которое равно квадрату двузначного числа и кубу однозначного числа.

Найдите два натуральных числа, сумма которых равна 168, а их наибольший общий делитель равен 24.

Найдите все пары простых чисел, которые являются решениями уравнения х + у = 26.

234

Задачи повышенной трудности

Путь от А до В идёт З км в гору, 6 км под гору и 12 км по ровному месту. Этот путь мотоциклист проделал за 1 ч 7 мин, а обратный путь — за 1 ч 16 мин. Найдите скорость мотоциклиста в гору и под гору, если на ровном месте его скорость 18 км/ч.

ЗаДача Л. Н. Толстого. Вышла в поле артель косцов. Ей предстояло скосить два луга, из которых один был вдвое больше другого. Полдня вся артель косила большой луг, а на вторую половину дня артель разделилась пополам, и одна половина осталась докашивать большой луг, а другая стала косить малый луг. К вечеру большой луг был скошен, а от малого остался участок, который был скошен на другой день одним косцом, работавшим весь день. Сколько было косцов в артели?

Из двух городов А и В, расстояние между которыми 180 км, в 6 ч 20 мин вышли навстречу друг другу автобус и легковой автомобиль. Их встреча произошла в 7 ч 50 мин, Если бы автобус вышел на 1 ч 15 мин раньше, а легковой автомобиль на 15 мин позже, то они встретились бы в 7 ч 35 мин. Какова скорость автобуса и легкового автомобиля?

[i*] Из города А в город В в 8 ч 50 мин вышли два автобуса. В то же время из города В в город А выехал велосипедист. Один автобус он встретил в 10 ч 10 мин, а другой — в 10 ч 50 мин. Расстояние между городами 100 км. Найдите скорость велосипедиста, если скорость одного автобуса в 1— раза больше скорости другого.

Всадник и пешеход одновременно отправились из пункта А в пункт В. Всадник, прибыв в пункт В на 50 мин раньше пешехода, возвратился обратно в пункт А. На обратном пути он встретился с пешеходом в двух километрах от пункта В. На весь путь всадник затратил 1 ч 40 мин. Найдите расстояние от А до В и скорость всадника и пешехода.

Только что добытый каменный уголь содержит 2 ⁰/0 воды, а после двухнедельного пребывания на воздухе он содержит 12 ⁰/0 воды. На сколько килограммов увеличилась масса добытой тонны угля после того, как уголь две недели был на воздухе? Два брата ходят из школы домой с одинаковой скоростью. Однажды через 15 мин после выхода из школы первый побежал в школу и, добежав до неё, немедленно бросился догонять второго. Оставшись один, второй продолжал идти домой в 2 раза медленнее. Когда первый брат догнал второго, они пошли с первоначальной скоростью и пришли домой на 6 мин позже, чем обычно. Во сколько раз скорость бега первого брата больше обычной скорости ходьбы братьев?

235

Задачи повышенной трудности

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ

Как появилась алгебра

Алгебра как искусство решать уравнения зародилась очень давно в связи с потребностями практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений.

Слово «алгебра» возникло после появления трактата «Китаб аль-джебр валь-мукабала» математика и астронома из г. Хивы Мухаммеда бен Муса аль- Хорезми (787 — ок. 850). Термин «аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра».

До XVI в. изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появлялись постепенно. Знаки «+» и «—» впервые встречаются у немецких алгебраистов XVI в. Несколько позже вводится знак «х» для умножения. Знак деления «:» был введён лишь в XVII в. Решительный шаг в использовании алгебраической символики был сделан в XVI в., когда французский математик Франсуа Виет (1540—1603) и его современники стали применять буквы для обозначения не только неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика ещё отличалась от современной. Так, Виет для обозначения неизвестного числа применял букву Л^У(Numerus — число), для квадрата и куба неизвестного — буквы Q (Quadratus — квадрат) и С (Cubus — куб). Например, запись уравнения х ^з— 8х ²+ 16х = 40 у Виета выглядела бы так:

1С — 8Q + 16N aequ. 40 (aequali — равно).

В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, более или менее сходных с действиями над числами. Современная алгебра — один из основных разделов математики.

Исторические сведения

Школьный курс алгебры включает, кроме некоторых алгебраических сведений, отдельные вопросы из других разделов математики (функции, метод координат, приближённые вычисления, теория вероятностей и др.).

О функциях

В первой половине XVII в. в связи с развитием механики в математику проникают идеи изменения и движения. В это же время начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601—1665) и Рене Декарт (1596—1650) представляли себе функцию как зависимость ординаты точки кривой от её абсциссы. А английский учёный И с а ак Нь ю т о н (1643—1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.

Термин «функция» (от латинского functio — исполнение, совершение) впервые ввёл немецкий математик Готфрид Лейбниц (1646—1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем функцию обычно рассматривали как аналитическое выражение. Однако уже у швейцарского математика Иоганна Бернулли (1667—1748) и члена Петербургской академии наук знаменитого математика XVIII в. Ле онарда Эйлера (1707—1783) имеется и общее понимание функции как зависимости одной переменной величины от другой.

Формулы сокращённого умножения

Некоторые правила сокращённого умножения были известны ещё около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.

У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а ²», а «квадрат на отрезке а», не «ab», а «прямоугольник, содержащийся между отрезками а и Ь». Например, тождество (а + = а ²+ 2ab + b ²во второй книге «Начал» Евкл ида (Ш в. до н. э.) формулировалось так: «Если прямая линия (имеется в виду отрезок) как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключённым между отрезками». Доказательство опиралось на геометрические соображения (см. рис. 70).

Некоторые термины подобного геометрического изложения алгебры сохранились до сих пор. Так, мы называем вторую степень числа квадратом, а третью степень кубом числа.

237

Исторические сведения

О методе координат

Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений. Древнегреческий астроном Клавдий Птолемей (П в.) применил географические координаты (долготу и широту) для определения местонахождения мореплавателя. Идеей координат пользовались в Средние века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения.

Применять координаты в математике впервые стали П. Ферма и Р. Декарт. В 1637 г. вышла книга Р. Декарта «Рассуждения о методе», в которой наряду с общими философскими рассуждениями о материи значительное место уделяется «универсальной математике». В разделе этой книги «Геометрия» Р. Декарт предложил новый метод — метод координат, который позволил переходить от точки (в координатной плоскости) к паре чисел, от линии к уравнению, от геометрии к алгебре. Это была новая геометрия, которую в настоящее время называют аналитической геометрией. Заслуга Р. Декарта состояла в том, что он ввёл переменные координаты. Так, в уравнении ах + by = с буквы х и у стали рассматриваться не как неизвестные, а как переменные. Благодаря этому каждой прямой в координатной плоскости соответствует линейное уравнение ах + by = с (а или Ь — отличные от нуля числа) и наоборот.

Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные аналитически с помощью уравнений и формул, решать различные геометрические задачи с помощью алгебры.

Термины «абсцисса» и «ордината» и название «координаты» были введены в употребление Г. Лейбницем в 70—80-е гг. XVII в.

Вычислительные средства

С давних пор люди стремились облегчить вычисления. Самой древней «счётной машиной» были пальцы рук и ног, камешки и другие мелкие предметы. Ремесленники и торговцы пользовались для счёта доской, разграфлённой на столбцы, на которой с помощью камешков откладывались единицы различных разрядов. Эту доску называли абаком. От римлян к нам пришло слово «калькуляция», что означает буквально «счёт камешками». Усовершенствование абака привело к появлению счётов (в Древнем Китае « суан-чан» , в Японии — «сорабан»). Русские счёты появились в XVI в.

Машину для механического производства арифметических действий называют арифмометром. Одними из первых таких машин

Исторические сведения

были машины, созданные в 1641 г. французским учёным Блезом Паскалем (1623—1662) и в 1671 г. Г. Лейбницем. Массовое распространение получил арифмометр, сконструированный в 1874 г. петербургским механиком В. Однером.

Революцию в вычислительной технике совершили электронные вычислительные машины (ЭВМ), которые появились в середине ХХ столетия. Первая ЭВМ была создана в США в 1944 г. Первая советская ЭВМ была построена под руководством академика С. А. Лебедева (1902—1974) в 1950 г. Современные ЭВМ производят несколько миллионов операций в секунду и находят широкое применение в различных областях науки и народного хозяйства. Простейшей ЭВМ является калькулятор.

239

Исторические сведения

СВЕДЕНИЯ ИЗ КУРСА

МАТЕМАТИКИ 5-6 КЛАССОВ

Делимость чисел

1. Пусть а и Ь — натуральные числа и при делении а на Ь в частном получается q и в остатке r. Тогда а = bq + r, где q и — натуральные числа или нули, причём r < Ь. Например:

127

105 127=35. з + 22.

2. Если натуральное число а делится на натуральное число Ь, то а называют кратным Ь, а Ь — делителем а. Это означает, что а = bq, где q — натуральное число. Например, 62 кратно 31, 31 — делитель 62, так как 62 = 31 • 2.

З. Простым числом называется такое натуральное число, которое имеет только два делителя — единицу и само это число.

Составным числом называется такое натуральное число, которое имеет более двух делителей.

Например, числа 2, 7, 43, 109 — простые, а числа 4, 12, 35 — составные. Число 1 не является ни простым, ни составным.

Всякое составное число можно разложить на простые множители, и притом единственным способом. Например, 630 = 2 • 3 ²• 5 • 7.

4. Чтобы найти наименьшее общее кратное нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем. Например, 72 = 2 ³• 3 ²• 180 = 2 ²• 3 ²• 5 и 600 = 2 ³• З • 5 ². Наименьшее общее кратное чисел 72, 180 и 600 равно 2 ³• 3 ²• 5 ²—- 1800.

Чтобы найти наибольший общий делитель нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем. Например, наибольший общий делитель чисел 72, 180 и 600 равен 2 ²• З, т. е. числу 12.

240

5. Если число оканчивается цифрой О или цифрой 5, то оно делится на 5. Если число оканчивается любой другой цифрой, то оно не делится на 5.

Если число оканчивается чётной цифрой, то оно делится на 2.

Если число оканчивается нечётной цифрой, то оно не делится на 2. Если сумма цифр числа делится на З, то и число делится на З.

Если сумма цифр числа не делится на З, то число не делится на З.

Если сумма цифр числа делится на 9, то и число делится на 9. Если сумма цифр числа не делится на 9, то и число не делится на 9.

Обыкновенные дроби

6. Правильной дробью называется дробь, у которой числитель меньше знаменателя.

Неправильной дробью называется дробь, у которой числитель больше знаменателя или равен ему.

7. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

8. Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное знаменателей дробей; вычислить дополнительные множители, разделив наименьшее общее кратное на каждый знаменатель; умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель. Например, приведём к наименьшему общему знаменателю дро-

1 7 5

би Наименьший общий знаменатель равен 36:

6 ' 12 ' 18

16 7 7 - 3 21 5 5 - 2 10

36' 12 12 - 3 36 ' 18 18 - 2 36 •

9.При сложении дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель. При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель.

5 4 1

Например, —

При сложении и вычитании дробей с разными знаменателями сначала их приводят к общему знаменателю.

10. Чтобы перемножить две дроби, надо перемножить отдельно их числители и знаменатели и первое произведение сделать числителем, а второе — знаменателем. Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.

Например,

5 6

Десятичные дроби

11. При округлении десятичной дроби до какого-нибудь разря-

да все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра 5, 6, 7, 8 или 9, то к последней оставшейся цифре прибавляют 1. Если первая следующая за этим разрядом цифра О, 1, 2, З или 4, то последнюю оставшуюся цифру не

изменяют.

Например, 4,376 4,4, 2,8195 2,820, 10,1425 10,14.

12. Сложение и вычитание десятичных дробей выполняют поразрядно. При этом дроби записывают одну под другой так, чтобы запятая оказалась под запятой. Например:

3,4691	68,3
48,63	5,275

52,0991 63,025

13. Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, а затем в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой в обоих множителях вместе.

Чтобы разделить десятичную дробь на десятичную, надо в делимом и делителе перенести запятые вправо на столько цифр, сколько их после запятой в делителе, а затем выполнить деление на натуральное число. Например:

3,06 12,096 : 2,24 = 1209,6 : 224, х

224

1209,6

1224 1120

612	89 6
7,344	-89 6

14. Чтобы умножить десятичную дробь на 10^п, надо в этой дроби перенести запятую на п цифр вправо. Чтобы разделить десятичную дробь на 10^п, надо в этой дроби перенести запятую на п цифр

влево.

Например, 8,373 • 100 = 837,3, 3,4 : 1000 = 0,0034.

Положительные и отрицательные числа

15. Модулем положительного числа и нуля называется само это число. Модулем отрицательного числа называется противоположное ему положительное число. Модуль числа а обозначают lal. Например, 13,6' = 3,6, lol = о, 1-2,81 = 2,8.

242

16. Чтобы сложить два отрицательных числа, надо сложить их модули и перед полученным результатом поставить знак «минус».

Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед полученным результатом поставить знак того слагаемого, модуль которого больше.

Сумма двух противоположных чисел равна нулю.

Например,

-3,4 + (-1,8) = -5,2, 2,5 + (-4,1) = -1,6, -3,6 + 3,6 = о.

17. Чтобы из одного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому. Например, —5 — 1 , 9 = —5 + (—1 9) 6,9.

18. Чтобы перемножить два отрицательных числа, надо перемножить их модули.

Чтобы перемножить два числа с разными знаками, надо перемножить их модули и перед полученным результатом поставить знак «минус».

Например, —1,2 • (—8) = 9,6, —3 • 1,2 = —3,6.

19. Чтобы разделить отрицательное число на отрицательное, надо модуль делимого разделить на модуль делителя.

Чтобы разделить два числа с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным результатом поставить знак «минус».

Например, —4,8 : (—2,4) = 2, 5,5 : (—5) 1,1.

20. Средним арифметическим нескольких чисел называется частное от деления суммы этих чисел на число слагаемых.

Пропорции

21. Равенство двух отношений называют пропорцией. Например, равенство 2,5 : 5 = 3,5 : 7 — пропорция. Числа 2,5 и 7 — крайние члены пропорции. Числа 5 и 3,5 — средние члены пропорции. Если пропорция верна, то произведение её крайних членов равно произведению средних членов. В пропорции можно менять местами крайние члены или средние члены.

22. Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Если величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

23. Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Если величины обратно пропорциональны, то отношение значений одной из величин равно обратному отношению соответствующих значений другой величины.

из

Свойства действий над числами

24. Переместительное свойство сложения. От перестановки слагаемых значение суммы не изменяется.

Сочетательное свойство сложения. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.

Переместительное свойство умножения. От перестановки множителей значение произведения не изменяется.

Сочетательное свойство умножения. Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.

Распределительное свойство умножения. Чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и сложить полученные результаты.

Преобразование выражений

25. Слагаемые, которые имеют одинаковую буквенную часть, называются подобными слагаемыми.

26. Для того чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Например, 5а — 7а + 4а = 2а.

27. Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки.

Например, 3х + (2а — у) = 3х + 2а — у.

28. Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.

Например, 5а — (2х — Зу) = 5а — 2х + Зу.

Список дополнительной литературы

1. Ага ханов Н. Х. Математика. Районные олимпиады. 6—11 классы / Н. Х. Агаханов, О. К. Подлипский. — М.: Просвещение, 2010.

2. Ба ври н И. И. Старинные задачи / И. И. Баврин, Е. А. Фрибус.

М.: Просвещение, 1994.

З. Волошинов А. В. Мудрость Эллады / А. В. Волошинов. — М.: Просвещение, 2009.

4. Всероссийская олимпиада школьников по математике. Смотрите в Интернете по адресу: www.problems.ru/

5. Галкин Е. В. Задачи с целыми числами: 7—11 кл. / Е. В. Галкин. — М.: Просвещение, 2011.

6. Гле й зер Г. И. История математики в школе: VII—VIII кл. / Г. И. Глейзер. — М.: Просвещение, 1982.

7. Государственная (итоговая) аттестация выпускников 9-х классов в новой форме. 9 класс. Смотрите в Интернете по адресу: www.fipi.ru

8. Д ор о фее ва А. В. Страницы истории на уроках математики / А. В. Дорофеева. — М.: Просвещение, 2007.

9. Игнатьев Е. И. В царстве смекалки, или Арифметика для всех. Кн. 1 / Е. И. Игнатьев. — М.: Просвещение, 2008.

10. И гнать ев Е. И. В царстве смекалки, или Арифметика для всех. Кн. 2 / Е. И. Игнатьев. — М.: Просвещение, 2008.

11. Игнатьев Е. И. В царстве смекалки, или Арифметика для всех. Кн. З / Е. И. Игнатьев. — М.: Просвещение, 2008.

12. Московский центр непрерывного математического образования. Смотрите в Интернете по адресу: www.mccme.ru/ Рекомендуем рубрики: «Олимпиады для школьников», «Журнал „Квант”».

13. Перел ь ман Я. И. Занимательная алгебра. Занимательная геометрия / Я. И. Перельман. — М.: АСТ, Астрель, 2002.

14. П и чури н Л. Ф. За страницами учебника алгебры / Л. Ф. Пичурин.

М.: Просвещение, 1999.

15. С пива к А. В. Тысяча и одна задача по математике: кн. для учащихся 5—7 кл. / А. В. Спивак. — М.: Просвещение, 2010.

16. Стройк Д. Я. Краткий очерк истории математики / Д. Я. Стройк.

М.: Наука, 1978.

Список дополнительной литературы

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

Аргумент 57 Приведение подобных членов 128

Прямая пропорциональность 70

Возведение в степень 94 произведения 103 Равносильные системы уравнестепени 104 ний 212

Выражение с переменными 8

График линейной функции 76 линейного уравнения с двумя переменными 205

прямой пропорциональности 71 уравнения с двумя переменными 204 функции 63

Графический способ решения систем уравнений 208

Деление степеней 100

Зависимая переменная 56

Корень уравнения 26

Коэффициент одночлена 108

Линейная функция 75

Линейное уравнение с двумя переменными 200

с одной переменной 28

Медиана 43

Многочлен 127 стандартного вида 128

мода 37

Независимая переменная 56

Область определения функции 57

Одночлен 108 стандартного вида 108

Основное свойство степени 99

Парабола 113

уравнения 26, 200

Разложение на множители многочлена 140

Размах 37

Распределительное свойство умножения 17

Решение системы уравнений 208

уравнения с двумя переменными 200

Свойства уравнений 27, 200

Сочетательное свойство сложения 17 умножения 17

Способ подстановки 211 сложения 215

Среднее арифметическое 36

Степень многочлена 128

одночлена 109 с натуральным показателем 93 с нулевым показателем 101

Тождественно равные выражения 20

Тождественные преобразования 21

Тождество 21

Угловой коэффициент прямой 78

Уравнение с двумя переменными 199

с одной переменной 26

Формула квадрата разности 164 — суммы 164 куба разности 165 — суммы 165 разности квадратов 177 — кубов 181

суммы кубов 180

Переменная 8 Функция 57

Переместительное свойство сложе-

Целое выражение 183

ния 17 умножения 17 Числовое выражение 5

Подобные члены многочлена 128 Член многочлена 127

246

Предметный указатель

ОТВЕТЫ

Глава

2. а) 20; 6) 28,89. З. а) 58; 6) 10. 9. 45 ц. 10. На 48 р. 19. 6) 1,3; 2,8; 5,8. 23. а) -4; 6) 5,2. 28. а) -49; 6) 0,8. 44. а) 60; г) 150. 45. 20 л. 46. 200 станков. 66. а) 4 ⁰/0 ; б) 15 ⁰/0 . 68. а) 26,81; 6) 77,01; в) 7,22; г) 78.

72. а) 35,7; 6) 16,64; в) 10; г) 2,8. 74. а) О; 6) 1 ⁴. 77. а) 35; 6) 124. 78. а) 94,2;

6) 40,3. 102. а) 6,75; 6) 22; в) -6; г) -0,3. 103. а) 11 - 6,5х; 6) зр - 5,1; в) 0,4а — 7; г) 6b — 5; д) у — 8; е) 8х — 8. 105. а) 8 + 2х; б) 46 — 5у; г) 5;

д) 4 - 10b. 106. а) 1; 6) -7. 109. На 12,5 ⁰/0 . 122. а) 4,5х - 2,4; 6) 36 - з,ба;

в) 12,3 - 8,5у; г) 2 - 14b. 128. а) 30; 6) 16; в) -6; г) З; д) -43; е) 180; ж) -5;

з) 300; и) -90. 129. а) 1 ²; б) 0,5; в) —2; г) О; д) —0,15; е) —5; ж) 12; з) —3; з

м) О. 130. а) 7; 6) 1 1 г) 5; д) 1 ²; е) -1,2; ж) 1 ².

11 4 4 4

131. а) ²; 6) 2,5; в) —89; г) 0,5. 132. а) 2,4; 6) -12; в) -5; г) -1,5. 133. а) 7; 6

6) -32; в) -3; г) -1,8. 134. а) 4; 6) 2; в) 3,6; г) з!. 135. а) 16; 6) ²; в) 4

4 4

г) З ; д) З. 136. а) 5,5; б) 2,4; в) 10. 137. а), в), г) Корней нет; б) любое чис13 ло является корнем уравнения. 138. а) О; б), г) корней нет; в) любое число является корнем уравнения. 142. а) 5,9; б) —9,4. 143. 214 и 178 билетов. 144. 8 и 11 домов. 145. 6,3, 6,3 и 3,4 см. 146. 3127 и 3110 м. 147. 4, 8, 24 и 96 рупий. 148. 46 и 40 деталей. 149. 60 ООО р. 150. 16, 22 и 32 компьютера. 151. 400 г, 80 г, 75 г. 154. 55 и 11 кустов. 155. 20 км/ч. 156. 50 км/ч. 157. 8 дней. 158. 20 маляров и 8 плотников. 160. 1,5 кг. 161. 2,4 кг и 10 кг. 162. 20 и 40 кг. 165. -39. 171. -63 квт • ч. 172. 291 кг. 173. 17. 174. 14,25. 175. 15. 176. а) 28; 6) 43 или -10. 180. ц/га. 185. 80 стра-

ниц. 199. б) Уменьшится на 9 ⁰/0 . 202. На 2596. 206. а) ^Ц; 6) 2,5; в) 240; з

207. а) 1,44; 6) 1 ²; в) 9,2; г) 6. 208. 207. 209. О. 210. а) ²; 6) -16.

7 18 4

211. а) -12,15; 6) 2,025; в) -16,2; г) 20,25. 223. а) 58; 6) 52. 224. а) О; 6) 3,947. 230. а) -0,5; 6) 1. 240. а) 1,49; 6) О; в) -32,5; г) 0,3. 241. а) 1; 7; б) —2; 9; г) —1; 1; 5; д) О; —3. 243. а) 24; б) —35; в), г) корней нет. 244. а) —5; б) 1. 247. 575 кроликов, 425 кур. 248. 42 куста. 249. 48 и 12 марок. 250. 10 дней. 251. 9 дней. 252. 13. 253. 8,75. 255. 8 и 16. 256. ЗО и 50.

Ответы

Глава П

276. а) 43,2 г; 6) 360 см ^з. 277. а) 390 км; 6) 60,5 км/ч. 278. а) 18 км;

б) 2,5 ч. 280. 165 книг. 294. а) 0,9; б) О; в) г) —2,5. 295. 200 машин.

303. Принадлежат точки В, С и D. 310. а) —1,76; б) 88. 323. а) (30; О);

6) (24; 0). 327. а) (1; 2); 6) (8; -6); в) (2; 28); г) (4,4; -6). 336. а) 2; 6) -13. 337. 20, 30, 15 деталей. 340. V= 20 — 2х, если О х < 9, 2, если 9 х 12. 352. у- 150 + 1,5х; а) 165; 6) 20. 364. при а = -0,4. 365. 2, З, 4 и 5. 367. а) (4; О); б) (—7; О); в), г) (О; О); д), е) не пересекает. 369. К = —0,4, принадлежит. 372. а) (7; 37); 6) -55); в) (1,2; 5); г) (140; 14). 373. Лежит.

Глава Ш

377. 6) 4096; г) 16 807. 384. д) -96; е) 432. 388. а) -9; 6) -37; в) -539. 391. а) 0,16; 0,81; 100; 6) 245; З; 453. 394. 18 и 90. 405. а) а ^ба ⁹, в) а ²а ¹³г) а ¹⁴а. 408. в) т ¹¹г) р ⁹; д) 10 ¹⁰, 410. в) 6 ¹⁷, г) 2 ¹⁴, 7

414. в) 0 ²⁰; з) 0,7 ⁵. 416. г) 1!; е) 8 . 417. г) 2 ²; д) -12 ²². 418. а) 49; 6) 81;

9 27 4 27

в) 25; г) 0,216. 419. а) х ^п+ 3 , в) х ^п+ 1 г) уп - 4. 420. а) З; б) —2,5; в) 90; г) —1. 424. 105 км. 427. 202,5 г. 436. г) (-ab) ³•, д) (20 ⁵,

е) е) 50 000 000. 439. д) х⁹•, е) х ^и. 441. в) 7

г) а ^2т; д) а 444. 6) 8 ²⁰, г) 32 ¹². 447, в) а ^и, г) х 20; д) т ²⁰. 450. а) 16;

459. а) -2; 6) 0,18. 460. а) 0,592; 6) 0,012. 461. 5т ²см ².

462. 8а ^зсм ^з. 463. а) 11; 6) З; е) О. 466. а) —¹; б) 0,5. 468. а) —3,3х⁴у ^З, б) —a ⁶b ⁴c;

в) 4х ³у⁴, г) —0,36a ⁵b ⁶x⁶. 469. в) 64a ⁵b ⁷, г) —28a ⁴b ⁴; д) —6х ⁶у³; е) 108a ⁴b ³472. в) —8a ¹²b ⁶; г) 81х⁸у ⁴; д) —a ¹⁰b ⁵c ¹⁵. 473. в) —0,216т ⁹п ⁶, г) 4х ²у^б; д) x⁴y ¹⁶b ⁸; е) -х ^1Оу ¹⁵т ⁵. 475. а) (9х ²) ². 476. в) 479. 6) 1000т ⁹; 100т ⁶480. а) 2250 ¹⁰, 6) 81b ²⁵, в) 8р ¹⁹; г) —0,158 ⁰; д) с ¹⁹е) 2b ¹³; ж) —х ¹⁰з) 2у ¹⁴.

481. Через 9 дней. 482. К = 1,5, Ь = 6. 498. х = —2,4, у = —20,4. 499. а) 4,8a ⁹b ¹⁰, 6) 28,8х ³у ¹²507. а) 45; 6) 88. 508. а) 5292; 6) 4851. 509. 8 чисел.

510. а) 4; 6) 5. 514. г) 3 ⁶; д) 2 ¹⁰. 515. в) 2 ⁵+ 2 ³+ 2. 519. а) 98; 6) -8.

527. —1,5. 531. в) + 3. 535. 6) 36; г) 0,6; е) -5 537. а) 2?; 6) 6,8.

9 з

542. в) 0,04,• г) 6,25; д) 1; е) 81. 543. в) Указание. 25 ²⁵= 550, 2 ⁵⁰• 3 ⁵⁰= 6 ⁵⁰

г) 63 ³⁰3 ⁶⁰. 5 ³⁰. 544. г) 3 ⁶. 560. г) за ⁸ь ⁷

Глава IV

572. а) 107; 6) 30. 573. а) -57; 6) З. 582. а) 233 ²; б) —1,6; в) -32. 583. а) ¹

з 7 5

584. а) 24 000; 6) -10 000. 587. г)

248

588. а) ода - 4,88; 6) 1,6х ²+ 5,5; в) -Н + 13b; г) 1,9у ²- 1,4у + 4. 593. а) х ²+ + 11 ху — у ²; б) а? — ЗаЬ + 56 ², в) 4с⁴- 78 + 6. 595. а) 0,20 ²+ + 1,2; б) 0,7у ²— 3,75y; в) —4х ²+ 4ху; г) 2ab ²— 4ab — 5b. 596. а) 4a ²b — Ь ²+ 2; б) 2ху. 597. а) 60; 6) 156. 598. а) -2; 6) -1. 601. а) 2ху - х ^и, 6) 2ху - у ². 604. а) 100 ²+

+ 12аь + 26 ²; 6) -48. 605. а) З; 6) 1 ²; в) 0,3; г) -20; д) О; е) 606. а) 1,23;

6) -2; в) -1,5; г) -2. 609. а) да; 6) да. 612. 6) -5а ⁸Ы; г) -2c ¹⁶d ⁷. 618. а) 10,5; 6) 28; в) 0,8; г) -5. 619. а) 80b - 11; 6) 5с + 34; в) -21; г) 42 - 24у. 620. а) 26у - 2у ², б) —у ²— 10у; в) 2 — 4х; г) 2а ^з, д) 4с²- 78, е) —3х3у; ж) 3т ^з— т ²п + 2n ²; з) п ²— п ^э. 621. а) 7х ²— 20х; б) а ^з+ а ²; в) ах ²— 8а ²х; г) 4т ⁴- - зп ⁴. 622. а) -6; 60; 6) 8. 623. а) 200; -250; 6) 0,8. 624. а) 140 ⁴- а ^з; 6) 26²— Ь; в) 16х ²— 6х ⁴; г) с ⁴. 630. а) 7; б) 8; в) 49; г) 0,4; д) —2; е) о; ж) 24; з) ^А. 631. а) -2; 6) -20; в) -1,5; г) -0,2. 632. а) -1; 6) 2;

в) -4; г) 2. 633. а) 0,5; 6) -2; в) 1,6; г) -2. 634. а) 24; 6) 13 ²; в) 1 ¹; г) —1 ²;

з з 8

д) —52,5; е) —4,5; ж) —36; з) 1 ²; и) 0,4. 635. а) 12,5; б) 17; в) 17; г) —25; д) —;

636. а) 6) -0,5; в) -2 ; г) 28. 637. а) -13; 6) 1,5; в) -15; г) 0,5.

13 4 7

638. а) -3,5; 6) -1; г) 2; д) 17,4; е) 4!. 639. 16, 20 и 8 см. 640. 60, 40

и 66 м ². 641. 28 флоринов. 642. 9 и З т. 643. ЗОО га. 644. 1500 м. 645. 9 км.

646. 40 км. 647. 360 км. 648. 19 г. 649. 8,8 кг. 653. а) ——а¹³у⁹; б) —90a ⁸b ⁹

660. а) 2,28; 6) -22,5; в) 14,4; г) -348. 661. а) О; -8; 6) О; 0,2; в) О; 5;

1 2

0,4; д) о; • е) О; -4; ж) О; 0,1; з) О; 30; и) О; - 662. а) О; -0,6;

11; в) О; 0,6; г) О; 10; д) О; 0,16; е) О; 0,04. 671. а) (Ь - -

б) (у — 5)(х + у); в) (2х — 7)(За — 56); г) (х — у)(х — у + а); д) (а — 2)(За — 5);

- - 17). 672. г) (с + + 9); д) (а - - Ь + 3); е) -(х + 2у) х х (4х + 8у + 1). 673. 9 км. 674. а) 5; 6) -1,5. 683. а) х ^з+ 2х ²у - у ^з; 6) Ю — 2п ²р + 2пр ²— р ^з; в) а ^з— 2ах ²— х ^з; г) Ы — 2b ²c + 8; д) а ^з— ба ²+ 11а — 12; е) 5х³— 7х ²— 3х + 2; ж) х^з+ 3х²— 8х + 10; з) Зу^з- 7у ²+ ту - 4. 684. а) с ^з— 2cd ²— Ю; б) х ^з— 2х ²у + у ^з; в) 4а ³— 3а ²+ 2а — З; г) —3х³+ 8х ²+ 7х — 12. 685. а) у ⁴+ 2у ^з- 15у ²; 6) -20 ⁴+ 80 ³- 68. 687. а) 196 - 10; 6) 14у²- 12; в) 9х; г) a ³b + 5ab ²— a ²b ², д) 4а — 2ab; е) 3х — у²- 2. 689. 9х + 1. 697. а) З;

6) 0,5; в) О; г) О. 698. а) • 6) 0,2; в) 3,5; г) 700. 21, 22, 23.

7 з

701. 17, 19, 21. 702. 25 и 10 см. 703. 36 см. 704. 12 дней. 705. 1680 га.

706. а) 2; б) 15,5. 711. е) (а + — З); ж) (х + у)(11 — х); з) (т + п)(К — п). 712. в) (т + К)(З — К); г) (х + у)(К — х). 713. а) — ²; б) —11 714. а) 12 ²; 6) О

16 36 з

718. а) (х + 5)(х + 1); б) (х — З)(х + 2); в) (а — 1)(а — 4); г) (а + 2)(а — 8).

249

719. 260 коров. 720. а) ——; 722. 6) -6; 2; в) -1; 1. 730. 1. 731. 8.

8 4

732. 71. 736. а) -7х ²- 14; 6) -8 + 2а + 2; в) -2а - 10b - З; г) -е. 745. а) -2; в) 0,5; г) 2. 746. 1,92; 3,84; 4,8; 5,76. 747. 11. 748. 52. 749. 246.

750. 417. 754. а) ²; 6) 2; в) 0,25; г) -3; д) 8; е) -3,5. 755. 1 кг. 756. 750 з и 800 кг. 757. 2! ч. 758. 2,5 ч; 150 км. 759. 60 км/ч; 50 км/ч; 210 км. з

760. 60 км/ч; 40 км/ч; 24 км. 761. 16,5 км/ч. 762. 2,5 км/ч. 763. 70 сорочек. 764. 600 и 800 т. 765. 480 га. 766. ЗО г. 770. а) 2,3; 6) 0,147.

771. а) О; - ²; 6) о; -1,6,• в) о; 2; г) о; 0,2; д) о; е) О; 1. 772. а) + 2) ²,

6 8

г) -270 - 2) ³. 781. а) -35; 6) 156. 784. 8; 9; 10; 11. 786. 400 см ². 787. 360 см ². 788. 80 м ². 789. 55,25 см ². 790. а) -2,8; 6) 7; в) 91; г) -4,2; д) О; е) -50. 793. а) (х — 4)(х — 6); б) (х — 8)(х — 5); д) (х + 4)(х — З);

е) (х + 5)(х — 7). 796. а = —4.

Глава V

815. в) 198х - 81х ²; г) 14аь - 49; д) 14b; е) -188 - 162. 816. а) + 81; б) —10х + 1; в) 12х — 9; г) а ²+ 4ab. 817. б) 4а ²; в) —21Ь — 4; г) 14 — 5b; д) -28 + 4а + 14; е) -2у ²+ 19у - 40. 818. а) З; 6) О; в) -14; г) 130. 819. а) 1,7;

1 в) З; г) 3,125. 820. а) 2,2; 6) 1; в) ²; г) 1. 821. д) 15с²- 24с + 20;

24 12

е) -168 + 26аЬ + 28. 822. 6) -96 + 48b - 68; в) -3х ²+ 2х - 12. 823. 6) 6х ⁵+ + 60х ⁴+ 150х ³; в) а ^з— За + 2; г) х ^з— 12х — 16. 826. а) При х = 16; б) при х = о. 829. а) 18х ²+ 54; 6) а ^з- 832. 80 и 90 км/ч. 840. а) 10 000;

144; 0,16; 6) 400; 25; 81; в) 81; 9; 1. 846. 6) н- ^Уа 865. а) 49;

6) 16. 870. 6) Ь ²+ 9; в) х ²+ 1; д) 75х ²+ 16; е) 138 + 49. 871. д) 50п ²- 49;

е) 5х ²+ 0,25. 873. а) —4 — 5х; б) —4m + 9; в) 18х ²— 2ах — а? ; г) 2ab + b ²— 2а ²; ж) 32у ²— 24ху; з) —8а ²— 24ab. 875. а) 2а ²— 40а + 12; б) 1 — 12b

- 108; в) 63р ²; г) 28ху - 98у ². 876. а) -1,5; 6) 7. 877. а) О; 6) -0,5. 881. а) -6;

6) 5; г) 2; д) 2,3. 882. 85 и 90 км/ч. 887. а) ^ё; б) 4 ⁴; в) —4; г) 1. 888. д) —1

4 7 5

е) 5. 890. а) 4 и —4; б) 9 и —9; в) ! и 1 г) 0,5 и —0,5; д) корней з

нет; е) 1 и —1; ж) 1,5 и —1,5; з) ⁴и 4 и) корней нет. 891. а) 5 и -5;

895. а) (у - + 1); 6) (с + - 7с)•,

в) —(х + у)(15х + у); г) —ЗЬ(1Оа - З»; д) 3b(3b - 48); е) - З“). 896. а) (2b - 11)(2b + 1); 6) -(4 + + за); в) (3 -11 т);

250

г) —ф + 1)(Зр + 1); д) 5с(5с — 6d); е) —9b(2a ²+ 96), 899. 38 см. 903. а) 0,6; 6) -0,2. 904. 12 км. 914. а), 6) да. 915. 6) -0,64х²- 1,6ху ⁴- в) —0,098 + + 0,12cd - 0,048; г) 16х ²- 36х⁶. 917. а) -0,1; 6) 4,5. 920. в) -у ²- 14у - 31; г) х ²- 8х - 33. 925, а) 4; 6) З. 926. а) -1,5; 6) -2. 928. а) —3у⁴+ 4у ³

- - 100; 6) 2а + 2. 932. ЗО км. 933. 6 км/ч. 942. а) - + 3); 6) - - а); в) -а(с + + 5); г) + + Ь). 943. а) - 2) х х (15 — а);в) с ³(а — 1)(с + 1); г) х (х — у)(х + 1). 946. а) (х + у)(х — у — 1); б) (а — + Ь — 1); в) (т + п)(1 + т — п); г) (К + р) х х (К -р - 1). 947. а) (а - + Ь + 1); 6) (с + - d + 1). 949. а) О; 1; -1; 6) О; З; -3; в) О; -1; г) О; 2; -2. 950. а) О; 6) О; 2. 954. а) 4,6; 6) 19,75.

963. а) 19; 6) 15. 964. 64. 968. а) 1; 6) 973. а) 50 - 4; 6) 70 - 9; зо

в) -2b - 1; г) + 1; д) 28 - 82; е) 75. 975. в) 50 ²- - 15; г) -4b - 13; д) -210 ²+ 21; е) 188 - + 2; ж) 3х ²+ 22; з) 10у²- зоу + 85. 976. при

всех х. 978. а) 4; 6) 1,5; в) 2,625; г) О. 980. а) ^Ч; 6) 1 —. 1 982. д) 15(х - 1) х

64 2 80 х (3х - 1); е) (2п + - 4п); ж) (За + + 4); з) (-5х - 13). 985. а) 17,4; 6) 17. 989. а) (2х + + х + 1); 6) (у - 7); в) а (а ²— ЗаЬ + 3b ²); г) (3х — у) (3х²+ у?); д) (2а + — 5ab + b ²); е) (Ь + 2) х х (b ²- 26b + 244). 992. а) -4; 6) 0,5; в) 2; г) 2. 994. а) 34,5; 6) 24. 999. а) —а³— 1,5а ²— 1,5а + 17; б) 4m ⁶— т ⁴— 15m ³— 18m ²+ 81 т. 1000. а ⁸— - 2а ⁴ь⁴+ Ь⁸. 1003. а) 131; 6) 61; в) 24,125. 1005. а) при а = 1; 6) при а = -1. 1006. а) при Ь = 20; 6) при 1. 1011. а) - 6b)•, 6) 3(7b - с) х х (8 + 2); в) + - + х); г) 6(5а - + 4). 1013. а) 2; -2; -3;

1. 1015. а) (х — у)(х + у — 1,5); б) (х + а) х 2 х (х — а + 0,5); в) (2а — Ь) (2а + Ь— 1); г) (р + 4с)ф — 4с — 1); д) (а + Ь)(а — Ь + 6);

+ у — 7). 1016. а) (х + 2у)(х — 1)(х + 1); б) (2у — 5)(у — 2)(у + 2);

+ - 5); г) (х - - + 3). 1017. а) (а + + Ь); с)(11с — 9b); в) (х — у)(5х + у); г) (а + 1)(а — 9). 1018. а) (а — Ь — 5) х Ь + 5); д) (90 - ЗЬ + + ЗЬ - с); е) (bc - ь - с - + Ь + с - 1). 1019. а) (х + + ху + У ^Г); б) —(4х + у) (х ²+ ху + у²); в) (а — + 2b); г) ф — 1)ф ²— р + 1); д) (2b + 1)(4b²+ Ь + 1); е) (а — 5)(а ²+ а + 25). 1020. а) (х ²— ху + у ²)(х + у + 2); б) (а ²+ ab + — Ь + З); в) (а — + — ab + b ²);

г) (х + у) (х — + ху + у ²).

Глава

1034. (6; 6). 1035. а = З. 1036. 4 или 9 монет. 1037. 6 тетрадей. 1038. 4 глубокие и 6 мелких тарелок. 1039. 2 и 7; 4 и 4; 6 и 1 соответственно трёхкилограммовых и двухкилограммовых пакетов. 1041. 17; 28; 39. 1042. 26. 1043. а) 6,16; 6) -4,32. 1044. а) (1 + - а); 6) (2 - + 0 ². 1051. -7,4.

251

2 511

1052. 11. 1054. а) 12; 6) 26,5. 1055. а) -1; 6) 34- 1065. а) з 12 12

1066. а) 108 - 178 + 19с - 40; 6) 21т ²+ шт- 8 . 1067.

6) + + - 3). 1069. а) (2; 5); 6) (1; -2); в) (4; 2); г) (4,5; 7); д) (-23; -3); е) (7; -4,5). 1070. а) (5; 2); 6) (1; 6); в) (-20; -2), , ; -3,5). 1071.

0= 0,2; б)р= З, q= 5; в) и =4!, - 2,25, q = -3,5. 1072. а) (-4; 3);

6) 7); в) (-10; 5); г) (—11 — 1073. а) (3; 0,5). 1074. а) -2 ¹

3 3

6) (-0,4; -7,2). 1075. а) (4,4; 1,72);

- -3, Ь = 1. 1077. а) х = -6, у = 4; б) а = 12 Ь

-5. 1078. а) (-15; 12); 6) (2; -1,5). 1082. а) (2; 1) б)

1083. ; 6) 0); в) (-5; 10); г) (-3; -3,5).

в) а = - ¹,

2 = -7. 1085. а) х = 1, у б) и = З, u = —10; в) х = —4, у = —1; г) а = 10, Ь = 5. 1086. а) х = 100, 1; б) и = 6, v = 5; в) х = 0,4, у : -0,2; г) ОД, Ь = 0,3. 1087. а) у ; 1,6х - З; 6) У -— 6х — 23; в) у = — 1 5х + , 11; г) у = 2х - 7.

1088. 2,2х + 11. 1089. = + 1-2 1090 . у = -2 ²х + 11. 1092. а) (7; -2);

6) (2; 1). 1093. а) х = З, у = 4; 6) х = 6, 20; в) т = 10, п = 12; г) и = 12, и = 15. 1094. а) (9; 8); 6) (-0,8; -0,8); в) (3; 4); г) 0). 1095. а) х = 15, у = 12; б) и — —8, 0 = 6; в) х = 12, у = -12; г) а 15, Ь = 10. 1098. а) -10х - 1; б) —6у + 4. 1099. 12 и 7 га. 1100. 575 и 740 изделий. 1101. 15 автомобилей. 1102. 23,77 и 10,97 м. ПОЗ. 12 см. 1104. 5 и 7 мешков. 1105. 40 и 170 рупий. 1106. 18 и 10 лет. 1107. 120 и 180 деталей. 1108. 60 км/ч. 1109. 45

и 5 км/ч. 1114. 33 и 22 книги. 1115. 35,75 и 29,25 г. 1116. 7,8 и 8,3 г/см ^з

1117. 720 и 1200 га. 1118. 320 и 360 деталей. 1119. 1,65 и 1,35 л. 1120. 37 000 и 8000 р. 1121. 48 и 32 г. 1122. 360 и ЗОО г. 1123. На 64. 1124. в) (р ²+ 2)ф ⁴— 2р ²+ 4); г) (З — + 3m ²+ т ⁴). 1135. 4 кв. ед. 1140. а) З; 6) 4. 1141. 6) (1; 18); (2; 9); (3; 6); (6; 3); (9; 2); (18; 1).

1142. (5; 37); (11; 31); (13; 29); (19; 23); (23; 19); (29; 13); (31; 11); (37; 5). 1143. 935. 1144. 214. 1145. 91. 1146. а) нет; 6) да, в точке (0; 9). 1147. 20. 1148. -0,88. 1158. (7; -2). 1159. 1160. 1161. 1,5. 1168. а) х = 21, у ; 25; 6) х = 1, у = 10; в) у = 16, 2 = 21; г) х = 9, у = 11; д) х = 10, у = 1; , , -0,2. 1169. а) (-0,25; 1); 6) (-0,5; 1,5); в) (7; 5);

г) (4; 4). 1170. 42, у- 17 17

252

1 1171. а) х = —5, у = З; б) и = О, и = 4. 1172. а) (5; —4); б), в), г) решез ний нет. 1177. 6 и 2 ч. 1178. З и 2 ч. 1179, 560 и 600 га. 1180. 15 и 12 см. 1181. 40 и 60. 1182. 50 и 60 кг. 1183. 20 и 15 деталей.

Задачи повышенной трудности

1184. 2, З, 4, 5, 7 и 13. 1185. а) -4; 10; 6) -11; 7; в) 2,5; 5,5; г) -1,3; 13,3.

1188. 1,25 кг. 1189. 520, 572 и 440 орехов. 1191. 96, 120 и 168. 1192. 36 и 48. 1193. 12, 24, 36, 48, 1194. Делится. 1196. 77. 1198. 890.

1202. 72. 1205. Первая дробь больше второй. 1213. 2 ⁶⁴- 1. 1218. 0= 5, Ь 2

7, а = -9. 1220. х = з, 2. 1121. а) х = З, у = 4, 2 = 5; 6) х = -4, у- 1,

5; в) х = -1, у = о, 1. 1222. 729. 1223. 24 и 144, или 48 и 120, или 72 и 96. 1225. 12 и 30 км/ч. 1226. 8 косцов. 1227. 40 и 80 км/ч.

1228. 15 км/ч. 1229. 6 км, 7,2 км/ч, 3,6 км/ч. 1230. =114 кг. 1231. В З раза.

S 1. ВЫРАЖЕНИЯ 1. Числовые выражения	5
2. Выражения с переменными	8
З. Сравнение значений выражений	12
S 2. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ 4. Свойства действий над числами . . . . . .	17
5. Тождества. Тождественные преобразования выражений . .	20
S З. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ 6. Уравнение и его корни . .	25
7. Линейное уравнение с одной переменной.	28
8. Решение задач с помощью уравнений .	32
4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ 9. Среднее арифметическое, размах и мода	36
10. Медиана как статистическая характеристика . Для тех, кто хочет знать больше 11. Формулы	42
Дополнительные упражнения к главе ГЛАВА П. ФУНКЦИИ	49
S 5. ФУНКЦИИ И ИХ ГРАФИКИ . 12. Что такое функция	55
13. Вычисление значений функции по формуле .	59
14. График функции .	62
6. ЛИНЕЙНАЯ ФУНКЦИЯ 15. Прямая пропорциональность и её график	69
16. Линейная функция и её график Для тех, кто хочет знать больше	75
17. Задание функции несколькими формулами	84
Дополнительные упражнения к главе П ГЛАВА Ш. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ	88
S 7. СТЕПЕНЬ И ЕЁ СВОЙСТВА 18. Определение степени с натуральным показателем	93
19. Умножение и деление степеней	99
20. Возведение в степень произведения и степени . .	103

254

Оглавление

S 8. ОДНОЧЛЕНЫ 21. Одночлен и его стандартный вид	108
22. Умножение одночленов. Возведение одночлена в степень	110
23. Функции у = х²и у = х^зи их графики. . . . Для тех, кто хочет знать больше	112
24. О простых и составных числах	119
Дополнительные упражнения к главе III ГЛАВА IV. МНОГОЧЛЕНЫ	121
9. суммА И РАЗНОСТЬ МНОГОЧЛЕНОВ . . 25. Многочлен и его стандартный вид	127
26. Сложение и вычитание многочленов . . . . .	130
10. ПРОИЗВЕДЕНИЕ ОДНОЧЛЕНА И МНОГОЧЛЕНА 27. Умножение одночлена на многочлен .	135
28. Вынесение общего множителя за скобки	140
S 11. ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ 29. Умножение многочлена на многочлен . 30. Разложение многочлена на множители способом	14 5
группировки . Для тех, кто хочет знать больше	150
31. Деление с остатком	152
Дополнительные упражнения к главе IV ГЛАВА V. ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ	155
12. КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ . . . 32. Возведение в квадрат и в куб суммы и разности двух выражений . 33. Разложение на множители с помощью формул квадрата	163
суммы и квадрата разности . . . . . . . . .	169
13. РАЗНОСТЬ КВАДРАТОВ. СУММА И РАЗНОСТЬ КУБОВ 34. Умножение разности двух выражений на их сумму .	172
35. Разложение разности квадратов на множители . . . . . . .	177
36. Разложение на множители суммы и разности кубов	180
S 14. ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ 37. Преобразование целого выражения в многочлен . 38. Применение различных способов для разложения	183
на множители Для тех, кто хочет знать больше	186
39. Возведение двучлена в степень	190
Дополнительные упражнения к главе V .	193

Оглавление

ГЛАВА VI. СИСТЕ ^МЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

S 15. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ

И ИХ СИСТЕМЫ 40. Линейное уравнение с двумя переменными	199
41. График линейного уравнения с двумя переменными	204
42. Системы линейных уравнений с двумя переменными . .	207
S 16. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ . 43. Способ подстановки	211
44. Способ сложения	215
45. Решение задач с помощью систем уравнений Для тех, кто хочет знать больше 46. Линейные неравенства с двумя переменными	219
и их системы. .	223
Дополнительные упражнения к главе VI	226
Задачи повышенной трудности . . . . . . , . . . . . . . . . .	232
Исторические сведения .	236
Сведения из курса математики 5—6 классов	240
Список дополнительной литературы	24 5
Предметный указатель	246
Ответы	247

Учебное издание

Макарычев Юрий Николаевич

Миндюк Нора Григорьевна Нешков Константин Иванович Суворова Светлана Борисовна

АЛГЕБРА

7 класс

УЧЕБНИК ДЛЯ ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЙ

Зав. редакцией Т. А. Бурмистрова. Редактор Т. Г. Войлокова.

Младший редактор Е. В. Трошко. Художники В. А. Коршунов, В. В. Костин.

Художественный редактор О. П. Богомолова. Компьютерная графика И. В. Губиной.

Технический редактор и верстальщик А. Г. Хуторовская.

Корректор Л. С. Александрова

Налоговая льгота — Общероссийский классификатор продукции ОК 005-93 — 953000. Изд. лиц.

Серия ИД N2 05824 от 12.09.01. Подписано в печать 12.07.12. Формат 70х 90 ¹/16. Бумага офсетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 14,30 + 0,47 форз. Тираж 80 ООО экз. Заказ № 32710 (П гэ).

Открытое акционерное общество «Издательство • Просвещение.. 127521, Москва, 3-й проезд Марьиной рощи, 41.

Отпечатано в полном соответствии с качеством предоставленных материалов в ОАО «Смоленский полиграфический комбинат». 214020, г. Смоленск, ул. Смольянинова, д. 1.

КВАДРАТЫ И КУБЫ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 10

(а + а²+ 2ab +

(а- a²-2ab + b²(а- Ь) (а + Ь) = a²-b²

(а + Ь) (a²-ab + b²) = а³+ b³

(а- Ь) (а²+ ab + Ы) = а^з- S

ТАБЛИЦА КВАДРАТОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 10 ДО 99

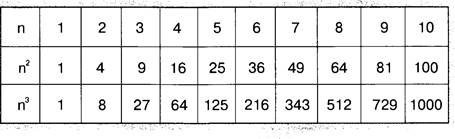
ДЕСЯТКИ					ЕДИНИЦЫ
ДЕСЯТКИ	О	1	2	з	4	5	6	7	8	9
1	100	121	144	169	196	225	256	289	З 24	361
2	400	441	484	529	576	625	676	729	784	841
2	400	441	484	529	576	625	676	729	784	841
з	900	961	1024	1089	1156	1225	1 296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	З 844	3969	4096	4225	4356	4489	4624	4761
6	3600	3721	З 844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Учебник по алгебре для 7 класса авторы Макарычев.Миндюк и др.

ФГОС ДЛЯ ОБЩЕОБРАЗОВАТЕЛЬНЫХ

Москва « Просвещение» 2013 удк 373

Данный учебник является первой частью трёхлетнего курса алгебры для общеобразовательных школ

Впервые вы узнаете о способах решения систем уравнений с двумя переменными

При работе с учебником рекомендуем использовать специальный диск, где предлагаются упражнения, которые вы можете выполнить на компьютере