Учебно-познавательный проект на тему "Возникновение геометрии"

МУНИЦИПАЛЬНОЕ  ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«КРУТОЯРСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»

Возникновение геометрии

Учебно-познавательный  проект

Автор проекта: Чернов Евгенй, ученик 7 класса

Наставник проекта: Каптилова В.А., учитель математики

2021 год

Содержание

Введение ………………………………………………………………………………3

1.      Возникновение геометрии …………………………………………………...4

2.      Возникновение геометрии в разных странах………………………………..5-11

2.1.            Геометрия Древнего Египта……………. ……………………………5-6

2.2.            Геометрия Вавилона………………………………………….. ….8

2.3.            Геометрия Древней Греции………………… …………………9-10

2.4.            Геометрия в Индии……………………………. ………………11-15

2.5.            Геометрия в Древнем Китае ………………………………………16

2.6.            Геометрия в странах Европы ……………………………………

 3. Этапы развития геометрии……………………………………………...

     4. Опроса по теме  "Ты. Геометрия. История"

Заключение ……………………………………………………………………16

Список литературы ……………………………………………………………17

Приложение …………………………………………………………………18-24

Введение

В 7 классе  у нас в  появился новый предмет, который называется «Геометрия». На первом уроке я узнал, что геометрия возникла очень давно, это одна из самых древних наук. Слово «геометрия» означает землемерие. В ее возникновении и развитии  важную роль играли эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни.

Все это меня очень заинтересовало. У меня появилось желание  узнать: Откуда берёт своё начало геометрия? Как появилась потребность в геометрии? Как добывались начальные геометрические сведения? Как и с помощью чего проводились измерения при зарождении геометрии? Какие учёные внесли вклад в развитие геометрии?

Целью проекта: изучение возникновения  геометрии в разных странах.

Задачи для достижения поставленной цели:

1.      Изучить литературу, Интернет-ресурсы об истории науки геометрии.

2.     Познакомиться с  применением геометрии древними людьми.

3.     Ознакомиться с историей становления геометрии в разных странах.

4. Составить и провести опрос на тему "Ты.Геометрия.История"

5.     Создать ментальную карту, изображающую основные страны, в которых происходило развитие геометрии.

6.     Составить словарь-справочник  происхождения некоторых геометрических терминов.

Актуальность выбранной темы в том, что геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Необходимость повседневного удовлетворения их ставит человека перед целым рядом вопросов о форме окружающих его предметов, вычислениях, связанных с землемерием, строительным делом и т.д.Несмотря на то, что возраст геометрии исчисляется тысячелетиями, геометрия и сейчас продолжает бурно развиваться. Она сохраняет важнейшее значение в наши дни. Она применяется в строительствах, технике, в практической жизни.

Практическая значимость проекта состоит в том, что материал проекта  может быть использован:

• учителями математики для проведения уроков геометрии, для проведения внеклассных мероприятий по математике.         

• учащимися для подготовки к уроку, написания реферата, продолжения исследований.

1.     Возникновение геометрии

Геометрия (греч. geometria, от ge — Земля и metreo — мерю) - раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре. Одна из самых древних наук, её возраст исчисляется тысячелетиями.

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т.д.

А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.

Но не только в процессе работы знакомились люди с геометрическим фигурами. Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

Для того, чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы. Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.

2.     Возникновение геометрии в разных странах

2.1.          Геометрия Древнего Египта

Имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры.

В древнейшие времена египтяне, приступая к постройке пирамиды, дворца или обыкновенного дома, сначала отмечали направление сторон горизонта. Действовали они следующим образом. Для того чтобы найти направление север - юг, втыкали вертикально палку и следили за ее тенью. Она становилась наименьшей, когда ее конец указывал на север.

В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон.

Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на двенадцать частей, а концы ее связывали. В направлении север-юг строители устанавливали два колышка на расстоянии четырех частей, отмеченных на веревке. Затем при помощи третьего колышка натягивали ее так, чтобы образовался треугольник, у которого одна сторона имела 3 части, другая 4, а третья - 5. Получался прямоугольный треугольник, площадь которого принимали за эталон, если пользовались одной и той же веревкой. При этом сторона, имеющая три части, указывала восточно-западное направление.

Таким образом, треугольник со сторонами 3, 4, 5 называется египетским треугольником.

Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый раз разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять емкость сосудов.

В Древнем Египте не было терминов «фигура», «сторона фигуры». Вместо этого использовались слова «поле», «границы поля», «длина поля».Однако и крупнейший историк древности Геродот, и философ Демокрит, и сам Аристотель именно Египет считали колыбелью геометрии.

Что умели древние египтяне: умели точно находить площадь поля прямоугольной, треугольной, трапециевидной формы. Умели строить прямоугольный треугольник. Знали, что отношение длины окружности к диаметру - число постоянное. Среди пространственных тел самым египетским можно считать пирамиду, хотя довольно близко они знакомы с кубом, параллелепипедом призмой и цилиндром, умели вычислять объем этих фигур.

Египетская геометрия была практической; в ней не столько рассуждали, сколько интуитивно устанавливали правила действий, удобные для приложений, но никогда их не исследовали.

2.2.          Геометрия Вавилона

Возделывание почвы в районах блуждающих Тигра и Евфрата, текущий с Армянского нагорья, требовало большого технического искусства и регулировки, чем в районе Нила. К тому же Двуречье было перекрестком многочисленных караванных путей. Вместе с товарами в Вавилон попадали знания других народов.

Шумеры писали на глиняных плитках, которые в большом количестве находят при раскопках. В табличках даны способы решения практических задач, связанных с земледелием,строительством и торговлей.

От вавилонян ведет начало деления круга на 360 градусов, деление градуса на 60 минут, минуты – на 60 секунд.

К задачам, которые вавилоняне решали алгебраическим и арифметическим методом, относятся и многие задания на определение длин, площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек. Все решения, встречающиеся в клинописных текстах, ограничиваются простым перечислением этапов вычисления в виде догматических правил: "делай то - то, делай так - то". В дошедших до нас вавилонских табличках имеются задачи абстрактного характера и внешне кажущиеся не связанными с практическими нуждами. Но это не так: они возникли в результате теоретической обработки условий, первоначально порожденных потребностями практики при межевании земель, возведении стен и насыпей, при строительстве каналов, плотин, оборонительных сооружений и пр. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Но соответствующие геометрические фигуры воспринимались ими как абстрактные, так прямоугольник они называли "то, что имеет длину и ширину", трапецию - "лбом быка", сегмент - "полем полумесяца", параллельные прямые - "двойными прямыми". У вавилонян не было таких геометрических понятий как точка, прямая, линия, поверхность, плоскость, параллельность. Измерение производилось при помощи веревки.

Основной чертой геометрии вавилонян был ее арифметико-алгебраический характер. Как и в Египте, геометрия развивалась на основе практических задач измерения, но геометрическая форма задачи обычно являлась только средством для постановки алгебраической проблемы.

Тексты глиняных табличек вавилонян содержат правила для вычисления площадей простых прямолинейных фигур и для объемов простых тел. Теорема Пифагора была известна не только для частных случаев, но и в полной общности.

Помимо простейших фигур, рассматривавшихся в Египте, математики Вавилона изучали некоторые правильные многоугольники, сегменты круга. Решались также задачи на подобие фигур. Пропорциональных отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна задолго до Фалеса. Это подтверждают клинописные таблички с задачами на построение пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов. Известно было и свойство средней линии трапеции.

 Древнеиндийская геометрия имела ярко выраженный практический характер и была тесно связана как с повседневными потребностями, так и с религиозными обрядами, в частности с культом жертвоприношения. В части дошедших до нас под названием « Сульва- сутра» священных древнеиндийских книг излагаются свойства фигур, связанных с построением алтарей-жертвенников.

 В этих книгах встречаются вычисления площадей, построения квадрата по данной его стороне, деление отрезка пополам, есть примеры практического применения подобия треугольников и теоремы Пифагора, которая имела следующую формулировку: «квадрат диагонали прямоугольника равен сумме квадратов его большей и меньшой сторон. Квадрат на диагонали квадрата в два раза больше самого квадрата».

В «Сутрах» правила и приемы приводят так же, как у египтян и вавилонян, без каких-либо объяснений.

2.3.          Геометрия древней Греции

Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?

Благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.

Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век.

Необыкновенный расцвет науки и культуры был тесно связан с общим подъемом греческого производства 6 - 4 в.в. до н.э., жизненными потребностями людей. Проблемы механики, астрономии, строительства, архитектуры, мореплавания требовали совершенствования математических методов, начиная от вычислительной геометрии и до учения об отношениях, способах определения площадей, объемов, центров тяжести.

Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку.

Большой вклад в развитие геометрии внесли известные древнегреческие учёные.

- Великий ученый Фалес Милетский основал одну из прекраснейших наук – геометрию. Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Фалес решил следующие задачи. Предложил способ определения расстояния до корабля на море. Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени. Доказал равенство углов при основании равнобедренного треугольника. Ввел понятие движения, в частности поворота. Доказал второй признак равенства треугольников и впервые применил его в задаче. Создал теорему о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.

Однажды, отправившись по торговым делам в Египет, он задержался там на несколько лет. Случилось так, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить. Фалес смог легко справиться с задачей. Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные изумились такому достаточно простому решению.

- Еще один древнегреческий математик, философ - Пифагор Самосский.

Он учился ге­ометрии у египтян, которые занимались ею с древних времен. Доказанная им  знаменитая теорема носит его имя – Теорема Пифагора. В некоторых древнегреческих источниках описывается радость Пифагора, когда ему удалось доказать теорему. В честь такого события он приказал принести жертву богам в виде сотни быков и устроил пир.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

-Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого учёного Евклида,жившего в Александрии в III веке до нашей эры. Центральное место среди античных трудов по геометрии занимают составленные около 300 до н. э. «Начала» Евклида.Первые четыре книги "Начал" посвящены геометрии на плоскости, и в них изучаются основные свойства прямолинейных фигур и окружностей.

Все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.Величайшая заслуга Евклида состоит в том, что он подвел итог построению геометрии и придал ей завершенную форму.

            - В III веке до н.э. жил еще один древнегреческий ученый Архимед.

Основные работы Архимеда касались различных практических приложений математики (геометрии), физики, гидростатики и механики. В труде «Об измерении круга» Архимед впервые вычислил число «пи» — отношение длины окружности к диаметру — и доказал, что оно одинаково для любого круга.

В области геометрии Архимед сделал открытие, которое поныне выражается в законе: «сегмент, шар и цилиндр с одинаковыми основаниями и при равных высотах относятся между собою, как 1, 2, 3», или, что «шар равен 2/3 описанного около него цилиндра». Это открытие доставило Архимеду так много радостей, что он изъявил желание иметь эпитафией на своем гробу шар, вписанный в цилиндр, найденный закон об отношении шара к цилиндру составляет предмет прекрасного трактата Архимеда «О шаре и цилиндре».

2.4.          Геометрия в Индии

Древнеиндийская геометрия имела ярко выраженный практический характер и была тесно связана как с повседневными потребностями, так и с религиозными обрядами, в частности с культом жертвоприношения. В части дошедших до нас под названием « Сульва- сутра» священных древнеиндийских книг излагаются свойства фигур, связанных с построением алтарей-жертвенников.

В этих книгах встречаются вычисления площадей, построения квадрата по данной его стороне, деление отрезка пополам, есть примеры практического применения подобия треугольников и теоремы Пифагора, которая имела следующую формулировку: «квадрат диагонали прямоугольника равен сумме квадратов его большей и меньшой сторон. Квадрат на диагонали квадрата в два раза больше самого квадрата».

В «Сутрах» правила и приемы приводят так же, как у египтян и вавилонян, без каких-либо объяснений.

Свой вклад в развитие геометрии в Индии внесАриабха́та (или Арьябха́та, санскр. आर्यभट, Кусумапури, 476—550) — индийский астроном и математик. Его деятельность открывает «золотой век» индийской математики.

Ариабхата написал свой трактат «Ариабхатия, когда ему было всего 23 года.

В первой части трактата воспроизводится таблица разностей синусов через 3°45′ = 225′, приведённая ранее в «Сурье-сиддханте».

В математической части трактата Ариабхата:

• описывает процесс извлечения квадратного и кубического корня в десятичной системе счисления;
• даёт формулы для площади круга и объёма сферы;
• приводит также приближённое значение для числа пи — отношения длины окружности к её диаметру.
• рассматривает вычисление гипотенузы прямоугольного треугольника по данным катетам и некоторые другие расчётные формулы, основанные на теореме Фалеса и теореме Пифагора;
• даёт решение квадратного уравнения, возникающего в задаче на сложные проценты;

 Значительную часть своей работы посвятил геометрииИндийский математик и астроном Брахмагупта (c.598 г. н.э. - ок. 668 г. н.э.).

Самый известный результат Брахмагупты в области геометрии - это его формула для циклических четырехугольников. Учитывая длины сторон любого вписанного четырехугольника, Брахмагупта дал приблизительную и точную формулу для площади фигуры.

2.5.          Геометрия в Древнем Китае

Самое древнее китайское математико-астрономическое сочинение «Чжоу-би», написанное около 1100 г. до н.э., в первой главе содержит предложение, относящиеся к прямоугольному треугольнику, среди которых – и теорема Пифагора. В этом же сочинении содержится правило для определения площади круга: «Умножь диаметр сам на себя, раздели на четыре, возьми три раза»

В трактате «Математика в девяти книгах» первая книга названа «Измерение полей» и содержит задачи на вычисление площадей земельных участков различной геометрической формы. Среди приведенных фигур имеются треугольники, трапеции, прямоугольники, круги, круговые сегменты, сектора и кольца. Правила вычисления площадей прямолинейных фигур в основном совпадают с современными, но терминология еще несовершенна; вместо понятия «трапеция» употребляется название «косое поле», вместо «сегмента» - «поле в виде лука» и т.д. Нет особого термина для радиуса, вместо него всегда задается диаметр.

Девятая книга трактата имеет название «Гоу-гу» - так назывались катеты прямоугольного треугольника, причем гоу–вертикальный катет, гу- горизонтальный катет. Все 24 задачи этой главы решаются по правилу «гоу-гу», связывающему катеты и гипотенузу прямоугольного треугольника, то есть по теореме Пифагора.

Один из известнейших геометров Древнего Китая ЛюХуэй. Он известен своими комментариями на «Математику в девяти книгах» (Цзю чжансуаньшу), которая представляет собой сборник решений математических задач из повседневной жизни. ЛюХуэй опубликовал «Цзю чжансуаньшу» в 263 году со своими комментариями, это старейшая сохранившаяся публикация книги. Самые известные труды ЛюХуэя:

·         Расчёт числа {\displaystyle \pi }Пи методом вписанных правильных многоугольников (англ.).

·         Расчёт объёма призмы, пирамиды, тетраэдра, цилиндра, конуса и усечённого конуса; метод неделимых.

2.6.          Возникновение геометрии в станах Европы

Принципиально новый шаг был сделан в геометрии  17 в. Р. Декартом.     Рене Декарт – философ, механик, математик, физик, физиолог, создавший аналитическую геометрию и современную алгебраическую символику.

Он ввёл в Геометрию метод координат. Метод координат позволил связать Геометрия с развивавшейся тогда алгеброй и зарождающимся анализом. Применение методов этих наук в Геометрия породило аналитическую Геометрия, а потом и дифференциальную.Аналитическая геометрия, также известная как координатная геометрия, включает размещение геометрической фигуры в системе координат для иллюстрации доказательств и получения информации с использованием алгебраических уравнений.

 Геометрия перешла на качественно новую ступень по сравнению с Геометрией древних: в ней рассматриваются уже гораздо более общие фигуры и используются существенно новые методы.

Cogito, ergosum – я мыслю, следовательно, я существую. Эта фраза сделала бессмертным Рене Декарта. После него осталось огромное наследие, причем в абсолютно разных отраслях науки, ему принадлежит открытие алгебраической символики, применяемой и сейчас, он оставил свой след в геометрии, физике и рефлексологии, но именно эта фраза содержит главную философскую идею, которой он придерживался всю жизнь.

Следующее большое развитие геометрии внес Иоганн Карл Фридрих Гаусс, которого  называли  королем математиков.

Карл Фридрих Гаусс первым построил основы неевклидовой геометрии и поверил в её возможную реальность. Однако за всю свою жизнь он ничего не опубликовал на эту тему, вероятно, опасаясь быть непонятым из-за того, что развиваемые им идеи шли вразрез с догматом евклидовости пространства в доминирующей в то время кантовской философией.

Вывод:Геометрия возникла как прикладная наука для решения практических задач. Страны, в которых и зарождалась геометрия, я представил в виде ментальной карты (Приложение 1)

3.     Этапы развития геометрии

Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э.

Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.

Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались. С этого времени начинается второй период развития Геометрии. Геометрия представлена так, как её в основном понимают и теперь, если ограничиваться элементарной геометрией; это наука о простейших пространственных формах и отношениях, развиваемая в логической последовательности, исходя из явно формулированных основных положений — аксиом и основных пространственных представлений. Геометрия, развиваемая на тех же основаниях (аксиомах), даже уточнённую и обогащенную как в предмете, так и в методах исследования, называется евклидовой геометрией.

Возрождение наук и искусств в Европе повлекло дальнейший расцвет Геометрии. Принципиально новый шаг был сделан в 1-й половине 17 в. Р. Декартом, который ввёл вГеометрия метод координат. Метод координат позволил связать Геометрия с развивавшейся тогда алгеброй и зарождающимся анализом. Применение методов этих наук в Геометрия породило аналитическую Геометрия, а потом и дифференциальную. Геометрия перешла на качественно новую ступень по сравнению с Геометрией древних: в ней рассматриваются уже гораздо более общие фигуры и используются существенно новые методы. С этого времени начинается третий период развития Геометрии.

Аналитическая геометрия изучает фигуры и преобразования, задаваемые алгебраическими уравнениями в прямоугольных координатах, используя при этом методы алгебры. К 1-й половине 17 в. относится зарождение проективной геометрии. Она возникла из задач изображения тел на плоскости; её первый предмет составляют те свойства плоских фигур, которые сохраняются при проектировании с одной плоскости на другую из любой точки. Окончательное оформление и систематическое изложение этих новых направлений Геометрии были даны в 18 — начале 19 вв. Эйлером для аналитической Геометрии (1748), Монжем для дифференциальной Геометрии (1795), Ж. Понселе для проективной Геометрии (1822).Во всех этих новых дисциплинах основы (аксиомы, исходные понятия) Геометрия оставались неизменными, круг же изучаемых фигур и их свойств, а также применяемых методов расширялся.

Четвёртый период в развитии Геометрии открывается построением Н. И. Лобачевским в 1826 новой, неевклидовой Геометрии, называемой теперь Лобачевского геометрией. Источник, сущность и значение идей Лобачевского сводятся к следующему. В геометрии Евклида имеется аксиома о параллельных, утверждающая: «через точку, не лежащую на данной прямой, можно провести не более чем одну прямую, параллельную данной». Многие геометры пытались доказать эту аксиому, исходя из других основных посылок геометрии Евклида, но безуспешно. Лобачевский пришёл к мысли, что такое доказательство невозможно. Утверждение, противоположное аксиоме Евклида, гласит: «через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две параллельные ей прямые». Это и есть аксиома Лобачевского. По мысли Лобачевского, присоединение этого положения к другим основным положениям Геометрия приводит к логически безупречным выводам. Система этих выводов и образует новую, неевклидову Геометрию.  Заслуга Лобачевского состоит в том, что он не только высказал эту идею, но действительно построил и всесторонне развил новую Геометрия, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям.

Главная особенность нового периода в истории Геометрии, начатого Лобачевским, состоит в развитии новых геометрических теорий — новых «геометрий» и в соответствующем обобщении предмета Геометрия. 

Так Геометрия превратилась в разветвленную и быстро развивающуюся в разных направлениях совокупность математических теорий, изучающих разные пространства (евклидово, Лобачевского, и т.д.) и фигуры в этих пространствах.

Вывод: В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.

Основные этапы развития геометрии я  отразили с помощью Ленты времени.

Заключение

Наука геометрия очень важна для человека. Геометрия развивалась за несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции. Большой вклад в развитие геометрии внесли известные учёные: Евклид и его книга под названием «Начала», Архимед, Пифагор, Фалес и другие ученые.

Геометрия возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.

Высокий уровень развития современной техники ставит перед геометрией все новые и новые задачи. В настоящее время геометрия определяется как часть математики, изучающая пространственную форму, размеры и взаимное расположение фигур.

Один великий человек как-то воскликнул: «Все вокруг геометрия!». Сегодня уже в начале 21 столетия мы можем повторить это восклицание еще с большим изумлением. В самом деле, посмотрите вокруг – всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника – все имеет геометрическую форму.

Таким образом, можно сделать вывод о том, чтороль возникновения геометрии в жизни человека неоценима.

Список литературы

1. «Википедия» свободная энциклопедия. http://ru.wikipedia.org/wiki/Заглавная_страница

2.Глейзер Г. И. История математики в школе 7-8 классы. Пособие для учителей.- М.:Просвещение,1982.

3.  Кордемский Б.А. Великие жизни в математике. - М.: Просвещение, 1995

4.Кольман Э. История математики в древности.

5. Феоктистов И. Геометрия до Евклида в очерках и задачах. – М.: Чистые труды, 2005.

6. Интернет-ресурсы:

- https://www.apxu.ru/article/geoforma/hi/4_etapa_razvitia_geometrii.htm

- https://wiki.mininuniver.ru/index.php/

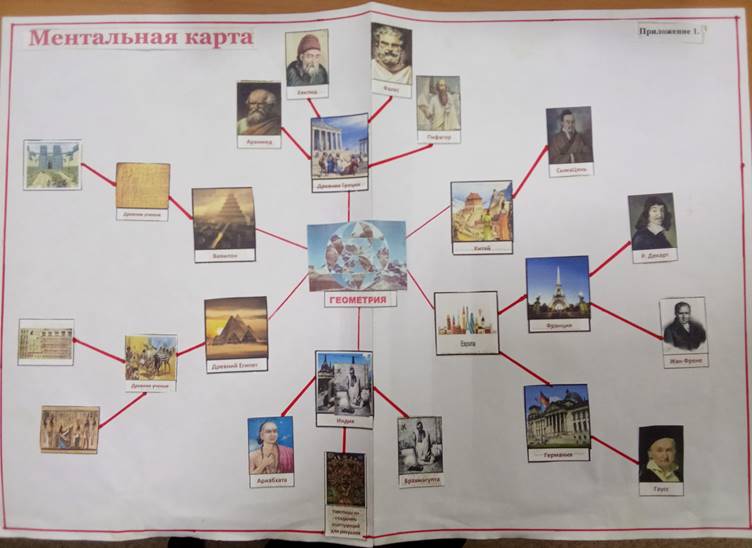Приложение 1

Ментальная карта стран, в которых зарождалась геометрия

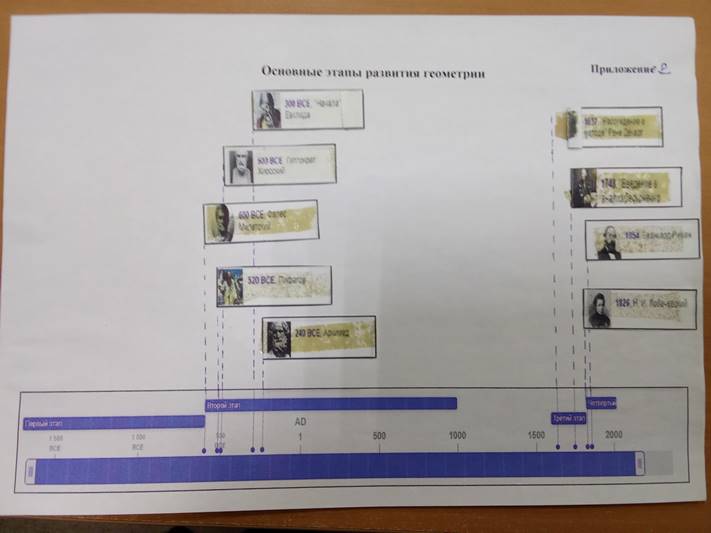Приложение 2

Основные этапы  развития геометрии

Приложение 3

Словарь-справочник  происхождения некоторых геометрических терминов

А

Слово «Аксиома»происходит от греческого axioma и обозначает в буквальном переводе на русский «значимое», «принятое» положение

Г

«Геометрия» в переводе с греческого языка означает  «измерение земли» или «землемерие».

«Гипотенуза» происходит от греческого слова «гипотенуза», что означает «тянущаяся под чем-либо».

Д

«Диагональ» происходит от слов «диа»  (через) и «гониа» ( из угла в угол).

С

Симметрия (с греч. «соразмерность», т.е. наличие определенного порядка, закономерности в расположении частей).

Слово «Сфера» происходит от греческого слова «сфайра» – «шар», «мяч»

П

 «Параллелограмм» введено Евклидом и состоит  из  «параллелос» - параллельный и «грамме» – линия

Понятие «Параллельные прямые» происходит от греческого слова παραλληλοζ которое означает «рядом идущий»;

В греческом языке «прямая» обозначалась словом ευθειου (эвтейон), которое означает «прямое, выпрямленное, прямая линия».

Слово «пирамида» происходит от греческого слова «пюрамис», которым греки называли египетские пирамиды.

Р

Слово «Радиус» происходит от латинского слова «радиус» – «луч», «спица в колесе».

«Ромб» происходит от греч.слова «ромбос», производного от глагола «рембеин» (вертеть, вращать).

«Рулетка» — термин французского происхождения (rouler — свертывать, катать).

К

«Катет» происходит от греческого слова «катетос», которое означает «отвес», «опущенный перпендикулярно».

Слово «конус» происходит от греческого слова «конос», что в переводе означает «сосновая шишка», «остроконечная верхушка шлема».

«Куб» происходит от греческого слова «кубос» - «игральная кость».

Т

Слово «точка»происходит от латинского глагола «ткнуть», а равнозначное слово «пункт» – от лат.слова «укол». В русском языке «точка»- конец заточенного гусиного пера.

Слово «трапеция» произошло от латинского слова «трапезиум» - столик. Раньше трапецией называли любой четырехугольник ( не параллелограмм).

Л

Слово «линия» происходит от латинского слова «линеа», которое произошло от «линум» – «лен», «льняная нить».

«Линейка» также происходит от лат. linea, linum – лен, льняная нить.

Ц

«Центр» произошло от греческого слова, обозначающего палку с заостренным концом, которой погоняли быков, а позднее – острие циркуля

Название «циркуль» позднего происхождения – оно происходит от лат. circulus – круг.

Скачано с www.znanio.ru