
Удержание частиц в зеркальной ловушке при наличии столкновений.
|
|
|
|
|
Fig. 1. A 100 eV electron beam is
injected into a neutral gas without applying external electric or magnetic
fields. The beam light starts very close to the cathode indicating that the
electrons acquire their full energy in a very thin cathode sheath. Thus, the
self-produced plasma acts as an anode. The initial beam convergence indicates
concave equipotential surfaces near the cathode, presumably due to a radial
density gradient. The beam scatters by collisions and beam-plasma
instabilities. |
|
|
|
|
|
Fig. 2. The beam is injected against a negatively biased grid. When the bias voltage is slightly larger than the cathode voltage most of the beam is reflected but a few electrons are transmitted. Note that the equipotential surface near the grid is not plane but convex. This causes an angular spread of the reflected electrons. Electrons in the center of the beam are normal to the sheath and can pass the grid when their energy exceeds the potential energy of the sheath. Рис.2 Пучок инжектируется в тормозящее электростатическое
поле создаваемое отрицательно заряженной сеткой. Когда приложенное к сетке
напряжение превышает напряжение катода большая часть электронов пучка
отражается от сетки, незначительная часть проникает за электродное
пространство. Следует отметить, что эквипотенциальная поверхность у сетки не
является плоской. Это обуславливает угловую расходимость отраженных
электронов. Электроны падающие на поверхность отражающей сетки ортогонально и
проникают в за электродное пространство когда их энергия превышает потенциал
сетки. |
|
|
|
|
|
Fig. 3. Beam injection against a very negatively
biased grid which reflects all electrons. Note dark sheath near grid where
the electron energy is decreased below 10 eV. The electrons stagnate in
the dark sheath and form a convex equipotential surface. This causes the
reflected beam to be highly divergent. |
|
|
|
|
|
Fig. 4. A 100 eV electron beam
injected perpendicular to a dc magnetic field. The sense of the cyclotron
orbit implies that the magnetic field points into the plane. From the beam
energy and the cyclotron radius the field strength can be calculated. Note
that the beam light weakens with propagation distance |
|
|
|
|
|
Fig. 5. A low energy beam is injected
across a magnetic field as in Fig. 1. The cyclotron radius is decreased.
Note the dark gap between the cathode and beam onset. In this sheath region
the electrons still have insufficient energy for light excitation. |
|
|
|
|
|
Fig. 6. A low energy beam is injected
against a decelerating electric field. As the beam energy falls below
10 eV the light emission stops. The beam and current continue to flow
through the dark region. |
|
|
|
|
|
Fig. 7. At high neutral pressures the
injected electron beam rapidly spreads. The electron mean free path can be
inferred from the beam decay. |
|
|
|
|
|
Fig. 8. Electron motion in crossed
electric and magnetic fields. The trajectory is a cycloid, i.e., a
superposition of a circular motion and a constant drift to the right. The
cyclotron orbit implies a magnetic field direction into the plane and the E×B
drift implies that the electric field points downward. From the known beam
energy the field strengths can be obtained from cyclotron radius and guiding
center drift. |
|
|
|
|
|
Fig. 9. Mirror reflection of a weak
electron beam in a nonuniform magnetic field. The beam is injected oblique to
the field lines which converge to the right. Due to the adiabatic invariants
(energy and magnetic moment) the parallel energy is converted into
perpendicular energy at which point the particles reflect. Alternatively, the
parallel motion is decelerated by the repelling force of an increasing
magnetic field. |
|
|
|
|
|
Fig. 10. Mirror reflection of a stronger
electron beam in a magnetic field which converges to the right. Note that the
guiding center (axis of spiral) of the reflected beam does not coincide with
that of the incident. This is due to the gradient and curvature drift in a
nonuniform field. |
|
|
|
|
|
Fig 11. Multiple reflections of an
oblique electron beam in a mirror magnetic field. The cyclotron motion is the
fastest periodic motion, followed by the slower bounce motion between the
mirror points. Gradient and curvature drifts cause a third, slowest rotation
azimuthally around the mirror axis. This is the classical charged particle
motion in the ionosphere in Earth's magnetic dipole field. Collisions and
other scattering processes diffuse the beam. |
|
|
|
|
|
Fig.12. Electron beam injected into a
nonuniform magnetic field with a null line. The beam meanders along a
magnetic null line pointing diagonally down to the right. Note the reversal
of the cyclotron rotation as the magnetic field reverses to either side of
the neutral line. Such meandering and figure-eight trajectories have been
studied theoretically in the problem of magnetic reconnection occuring in the
magnetosphere and on the sun. |
Если частицы в ловушке не сталкиваются между собой и не взаимодействуют между собой на расстоянии‚ то после вылета из ловушки частиц с вектором скорости‚ лежащим внутри конуса потерь‚ останутся только частицы‚ которые будут удержаны сколь угодно долго.
В реальности‚ однако‚ столкновения между частицами происходят и результате этих столкновений угол q может измениться и стать меньше‚ чем q0 (см. формулу 14.17). Тогда частица вылетит из ловушки. Поскольку вылетевшие частицы обратно не возвращаются‚ а из ловушки частицы время от времени вылетают (из-за столкновений)‚ то число частиц (плотность плазмы) в ловушке постепенно убывает с некоторым характерным временем t‚ которое и будет временем жизни плазмы в ловушке. Осуществить термоядерный синтез в ловушке можно лишь в том случае‚ если t будет достаточно большим‚ чтобы удовлетворить критерию Лоусона nt>1×1014 см-3с.
Простейшим видом взаимодействия между заряженными частицами являются кулоновские столкновения. Избежать этих столкновений нельзя (т.к. синтез ядер происходит именно при столкновениях)‚ поэтому время рассеяния частицы в конус потерь и является примерно временем между двумя кулоновскими столкновениями. Т.о. максимально возможное время удержания плазмы в зеркальной ловушке - порядка tii. Согласно (2.13)
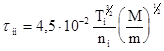 ‚ (2.13)
‚ (2.13)
где Т - °К; ni - см-3.
Более точное выражение для t было найдено Джаддом и.-Дональдом и Розенблютом и Будкером
![]() ‚ (15.1)
‚ (15.1)
где R - пробочное отношение. Эта формула справедлива для коротких ловушек‚ т.к. поле предполагалось параболическим (идея максвелловского распределения). Обычно R~r‚ т.е.
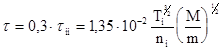 (15.2)
(15.2)
Критерий Лоусона для зеркальной ловушки‚ если такое время жизни достигнуто‚ выглядит
![]() . (15.3)
. (15.3)
Или для дейтерия (![]() )
)
![]() или
или ![]() кэВ (15.4)
кэВ (15.4)
Интересно‚ что в зеркальной ловушке критерий Лоусона не зависит от плотности‚ когда потери обусловлены кулоновскими потерями в конус потерь. Это связано с тем‚ что t~1/ni. Однако‚ как будет видно далее‚ время жизни может быть более коротким из-за поперечной диффузии и неустойчивостей‚ тогда выполнение критерия Лоусона требует достаточно высокой плотности. Кроме того‚ при такой высокой температуре излучение из плазмы (~sТ4!!!) настолько сильно‚ что плазма остывает прежде‚ чем произойдет достаточное число реакций. Следует отметить еще одно важное обстоятельство. Поскольку скорость теплового движения электронов намного выше‚ чем ионов‚ электроны быстрее рассеиваются в конус потерь и плазма принимает положительный потенциал‚ усиливающий уход ионов из ловушки. Величина этого потенциала определяется условием равенства скоростей ухода ионов и электронов:
Ф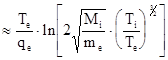 .
.
Этот эффект снижает “классическое время” жизни (15.2) в 2 - 3 раза.
Итак‚ верхний предел времени зеркальной ловушки (так называемое “классическое” время) составляет примерно
t=0‚1tii. (15.5)
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.