УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ

Умножение и деление степеней

Цели: продолжить формировать умение выполнять действия со степенями с одинаковыми основаниями.

Ход урока

I. Устная работа.

1. Найдите значение выражения.а) 4³;                     б) (0,7)²;                              в) ;                 г) 0¹²;

д) (–6)²;                       е) (–0,3)⁴;                           ж) (–1)⁸;                              з) .

2. Сравните с нулем значение выражения.а) (–25)¹² · (–25)⁹;б) (–4)¹⁹ : (–4)⁷;в) (–12)¹³ · (–12)⁸.

3. Замените звездочку степенью с основанием а так, чтобы стало верным равенство:

а) а⁴ · * = а¹²;            б) * · а = а⁴;в) а¹⁴ : * = а⁷;                            г) * : а⁹ = а¹⁰.

II. Формирование умений и навыков.

На этом занятии учащиеся отрабатывают умение делить степени с одинаковыми основаниями и решают комбинированные задачи.

1. № 414.

Решение:

а) x⁵ : x³ = x^{5 – 3} = x²; в) a²¹ : a = a^{21 – 1} = a²⁰;  з) 0,7⁹ : 0,7⁴ = 0,7^{9 – 4} = 0,7⁵.

2. № 416.

Решение:

а) 5⁶ : 5⁴ = 5^{6 – 4} = 5² = 25;  б) 10¹⁵ : 10¹² = 10^{15 – 12} = 10³ = 1000;  в) 0,5¹⁰ : 0,5⁷ = 0,5^{10 – 7} = 0,5³ = 0,125;

г) ;  д) 2,73¹³ : 2,73¹² = 2,73^{13 – 12} = 2,73;

е) .

3. Используя правила умножения и деления степеней, упростите выражение.

а) x⁸ ∙  x³ : x⁵;              б) x²⁰ : x¹⁰ ∙  x;   в) x⁷ : x³ : x³;                                       г) x¹⁴ : x⁹ ∙  x⁵.

Решение:

а) x⁸ ∙  x³ : x⁵ = x^{8 + 3} : x⁵ = x¹¹ : x⁵ = x^{11 – 5} = x⁶;  б) x²⁰ : x¹⁰ ∙  x = x^{20 – 10} ∙  x = x¹⁰ ∙  x = x^{10 + 1} = x¹¹;

в) x⁷ : x³ : x³ = x^{7 – 3} : x³ = x⁴ : x³ = x^{4 – 3} = x;  г) x¹⁴ : x⁹ ∙  x⁵ = x^{14 – 9} ∙  x⁵ = x⁵ ∙  x⁵ = x^{5 + 5} = x¹⁰.

4. № 417.

Решение:

а) = 8⁶ : 8⁴ = 8^{6 – 4} = 8² = 64;  б) = 0,8⁷ : 0,8⁴ = 0,8^{7 – 4} = 0,8³ = 0,512;

в) = (–0,3)⁵ : (–0,3)³ = (–0,3)^{5 – 3} = (–0,3)² = 0,09; г) ;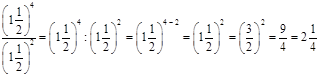

д) .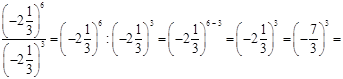

5. Найдите значение выражения.

а) ;                                      б) ;

в) ;                                          г) .

При выполнении этого упражнения уже не обязательно переписывать дробь в виде частного.

Желательно, чтобы учащиеся проговаривали не только правила действий над степенями, но и правила возведения в степень отрицательного числа при четном нечетном показателях.

Решение:

а) 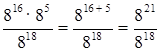 = 8^{21 – 18} = 8³ = 512;

б) 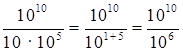 = 10^{10 – 6} = 10⁴ = 10 000;

в) 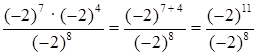 = (–2)^{11 – 8} = (–2)³ = –8;

г) 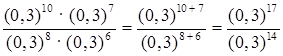 = (0,3)^{17 – 14} = (0,3)³ = 0,027.

6. № 419 (а, в, д).

Решение:

а) xⁿ ∙  x³ = x^{n + 3};

в) x ∙  xⁿ = x^{1 + n} = x^{n + 1};

д) c⁹ : c^m = c^{9 – m}.

7. Представьте данное выражение сначала в виде произведения степеней, а затем в виде частного степеней.

а) a^{m – 2};                       б) a⁴ⁿ;   в) aⁿ.

Решение:

а) a^{m – 2} = a^{m – 4} ∙  a²;                a^{m – 2} = a^m : a²;

б) a⁴ⁿ = a²ⁿ ∙  a²ⁿ;                      a⁴ⁿ = a⁵ⁿ : aⁿ;

в) aⁿ = a^{n – 1} ∙  a;                        aⁿ = a²ⁿ : aⁿ.

Выполняя это упражнение, учащиеся могут предложить свои варианты разбиения на множители.

8. № 420 (а, в), № 421 (а, б).

№ 420.

Решение:

а) если х = 2,6, то 3х⁰ = 3 (при любом значении х);

в) 10a²b⁰ = 10a², если а = 3, b = –8, то 10a² = 10 · 3² = 10 · 9 = 90.

№ 421.

Решение:

а) b⁴ · b⁰ = b⁴ · 1 = b⁴;             б) c⁵ : c⁰ = c⁵ : 1 = c⁵.

При выполнении этого упражнения учащиеся могут воспользоваться правилом умножения и деления степеней.

III. Итоги урока.

– Дайте определение степени с натуральным показателем.

– Сформулируйте правило возведения отрицательного числа в четную степень, в нечетную степень.

– Какой знак имеет результат возведения любого числа в квадрат?

– Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.

– Чему равно значение выражения 2⁰; (–1)¹; ?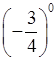

Домашнее задание:  № 415;  № 418;  № 419  (б, г, е);  № 420  (б, г);
№ 421 (в, г); № 422.