УМНОЖЕНИЕ ОДНОЧЛЕНА НА МНОГОЧЛЕН11

Умножение одночлена на многочлен

Цели: продолжить формирование умения умножать одночлен на многочлен; формировать умение выполнять данное действие при решении уравнений.

Ход урока

I. Устная работа.

1. Выполните умножение одночленов.

а) 2х⁵ · 3х²;                    в) (–3b) · (–7b);                 д) (х²)³ · 5х;            

б) –4a³ · a;                 г) y⁷ · (–3y);                     е) .

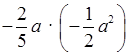2. Упростите выражение.

а) 2x (x² – 4x);               в) 4y;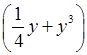

б) –а² (а + 8);                г) p²(2p – 4).

II. Формирование умений и навыков.

1. № 630 (а, в, д, ж).

2. № 631 (а, в).

Решение:

а) 3х (2х – 1) – 6х (7 + х) = 90;

    6х² – 3х – 42х – 6х² = 90;

    –45х = 90;

    х =;

    х = –2.

Ответ: –2.

в) 5x (12x – 7) – 4x (15x – 11) = 30 + 29x;

    60x² – 35x – 60x² + 44x = 30 + 29x;

    –35х + 44 х – 29х = 30;

    –20х = 30;

    х = ;

    х = –1,5.

Ответ: –1,5.

1. № 634 (а, в, д, и).

2. № 636.

3. № 637.

Решение:

б) .

Умножим обе части уравнения на 30:

;

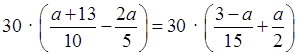3 (a + 13) – 6 · 2a = 2 (3 – a) + 15a;

3а + 39 – 12а = 6 – 2а + 15а;

–9а – 13а = 6 – 39;

–22а = –33;

а = ;

а = 1,5.

Ответ: 1,5.

г) .

Умножим обе части уравнения на 18:

;

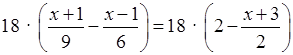2 (х + 1) – 3 (х – 1) = 36 – 9 (х + 3);

2х + 2 – 3х + 3 = 36 – 9х – 27;

–х + 9х = 9 – 5;

8х = 4;

х = .

Ответ: 0,5.

1. № 622.

2. № 629.

Решение:

Преобразуем данное выражение:

2x (x – 6) – 3 (x² – 4x + 1) = 2x² – 12x – 3x² + 12x – 3 = – x² – 3.

Очевидно, что при любом значении х значение выражения –х² будет неположительным, тогда значение выражения –х² – 3 будет отрицательным при любом значении х.

III. Итоги урока.

– Как выполнить умножение одночлена на одночлен?

– Сформулируйте правило умножения одночлена на многочлен.

– Как решить уравнение, в котором встречаются дроби?

Домашнее задание: № 632; № 634 (б, г, е, з); № 638; № 627.