УМНОЖЕНИЕ ОДНОЧЛЕНОВ

Умножение одночленов

Цель: формировать умение умножать одночлен на одночлен, используя правило умножения степеней с одинаковыми основаниями.

Ход урока

I. Устная работа.

1. Назовите коэффициент одночлена.

а) 15a²b²c; б) 18a³b²c;                         в) –24ab²c³;       г) –35ab³c²;д) nm²;         е) n³m; ж) –pqr²;             з) –pq²r.

2. Определите степень одночлена.

а) 37a²bx³; б) xyz;                            в) x²y;                    г) –862.

III. Объяснение нового материала.

1. Решим следующую задачу.

Объем  прямоугольного  параллелепипеда  вычисляется  по  формуле
V = abc, где а – длина, b – ширина и с – высота этого параллелепипеда.

Каким будет объем нового параллелепипеда, если длину данного увеличить в 5 раз, ширину – в 2п раз, высоту в 3п раз?

Решение:

Найдем измерения нового параллелепипеда:

длина – 5а;

ширина – 2пb;

высота – 3пс.

Тогда его объем равен (5а) · (2пb) · (3пс). Данное выражение является произведением трех одночленов. По правилам умножения можно записать равенство:

(5а) · (2пb) · (3пс) = 5а · 2пb · 3пс = (5 · 2 · 3) · (аппbс) = 30ап²bс =
= 30аbсп².

2. В результате умножения одночленов снова получается одночлен, который можно упростить, записав в стандартном виде:

(3a²b³c) · (4ab²) = (3 · 4) · (a²a) · (b³b²) · c = 12a³b⁵c.

3. Аналогично находим произведение трех и более одночленов.

IV. Формирование умений и навыков.

На уроке отрабатываются умения перемножать одночлены и раскладывать одночлен в виде произведения двух и более одночленов.

1. Выполните умножение.

1) а) 12у · 0,5у;                              б) 8x · 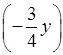;                      в) –b³ · 3b²;

2) а) xy² · 16y;           б) 1,6a²c · (–2ac²);                    в) –x³y⁴ · 1,4x⁶y⁵.

Решение:

1) а) 12у · 0,5у = (12 · 0,5) (у · у) = 6у²;    б) 8x² · (x²y) = –6x²y;    в) –b³ · 3b² = (–1 · 3)(b³b²) = –3b⁵;

2) а) xy² · 16y = (xy²y) = 12xy³;    б) 1,6a²c · (–2ac²) = (1,6 (–2))(a²cac²) = –3,2a³c³;

    в) –x³y⁴ · 1,4x⁶y⁵ = (–1 · 1,4)(x³y⁴x⁶y⁵) = –1,4x⁹y⁹.

2. Перемножьте одночлены.

а) (–0,4x⁵y⁶z²) · (–1,2xyz³);  б) (–2,5n⁴m⁵k²) · (3nm²k⁵); в) ;г) .

Решение:

а) (–0,4x⁵y⁶z²) · (–1,2xyz³) = (–0,4 · (–1,2)) · (x⁵x) · (y⁶y) · (z²z³) =
= 0,48x⁶y⁷z⁵;

б) (–2,5n⁴m⁵k²) · (3nm²k⁵) = (–2,5 · 3) · (n⁴n) · (m⁵m²) · (k²k⁵) = 7,5n⁵m⁷k⁷;

в)  · (x²x) · (y³y²) · (zz³) =
= 2x³y⁵z⁴;

г)  · (a²a³) · (b⁵b²) · (c³c⁴) =
= –7,5a⁵b⁷c⁷.

3. Перемножьте одночлены.

1) –20х⁴,   0,5ху²    и    –0,3х²у³; 2) 12x²y²z,   xy²z²    и    –0,1x²yz².

Решение:

1) (–20x⁴) · (0,5xy²) · (–0,3x²y³) = (–20 · 0,5 · (–0,3)) · (x⁴xx²) · (y²y³) =
= 3x⁷y⁵;

2) (12x²y²z) · 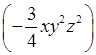 · (–0,1x²yz²) =  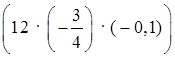· (x²xx²) ×
× (y²y²y) · (zz²z²) = 0,9x⁵y⁵z⁵.

4. Выполните умножение.

а) (–a) · (3b) · (4a²b) · (5ab²);  б) (5a) · (a²b²) · (–2b) · (–3a); в) (–1,5ab) ·  · (–2ac) · (24ab).

Решение:

а) (–a) · (3b) · (4a²b) · (5ab²) = (–1 · 3 · 4 · 5) · (aa²a) · (bbb²) = –60a⁴b⁴;

б) (5a) · (a²b²) · (–2b) · (–3a) = (5 · 1 · (–2) · (–3)) · (aa²a) · (b²b) = 30a⁴b³;

в) (–1,5ab) ·  · (–2ac) · (24ab) =  ×
× (aaa) · (bbb) · (cc) = 18a³b³c².

V. Итоги урока.