Упругие и не упругие столкновения

Упругие и не упругие столкновения

Виды взаимодействий

В механике одним из видов взаимодействия между телами являются соударения, или удары.

Удар — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии.

В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.

При ударе выполняется закон сохранения импульса.

Предполагается, что на время удара действием внешних сил можно пренебречь. Тогда полный импульс тел при ударе сохраняется. В противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тел и звук.

Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара.

Если не известны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначно движение тел после удара невозможно.

В общем случае решение задачи о столкновении, кроме знания начальных скоростей, требует дополнительных параметров.

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется.

В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно.

Пример:

хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.

Математическая модель абсолютно упругого удара работает примерно следующим образом:

1. Есть в наличии два абсолютно твёрдых тела, которые сталкиваются.

2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно и полностью переходит в энергию деформации.

3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации полностью обратно переходит в кинетическую энергию.

4. Контакт тел прекращается, и они продолжают движение.

Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии и закон сохранения импульса:   m₁u₂+m₂u₂=m₁v₂+m₂v₂;

где m₁, m₂ — массы первого и второго тела, u₁, u₂ — скорости тел до удара, v₁, v₂ — скорости тел после удара соответственно.

Импульсы складываются векторно, а энергии — скалярно.

Пример (отобразить в тетради):

частные случаи упругих ударов и их результаты:

 1. Абсолютно упругий удар тел равных масс (покоящегося и движущегося).

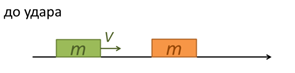
Рис. 4. Тела равных масс (покоящееся и движущееся) до удара

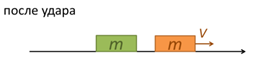
Рис. 5.  Тела равных масс (покоящееся и движущееся) после удара

2. Абсолютно упругий удар двух тел разных масс.

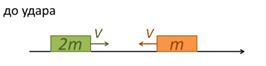
Рис. 6.  Тела разных масс до удара

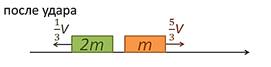
Рис. 7.  Тела разных масс после удара

3. Абсолютно упругий удар тел равных масс, но с различными направлениями и модулями скоростей.

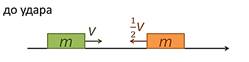
Рис. 8.  Двигающиеся навстречу друг другу с разными скоростями тела равных масс до удара

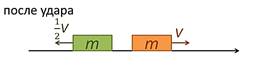
Рис. 9.  Двигающиеся навстречу друг другу с разными скоростями тела равных масс после удара

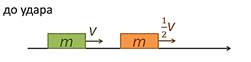
Рис. 10.  Двигающиесяв одном направлении с разными скоростями тела равных масс до удара

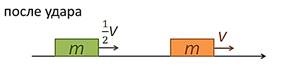
Рис. 11.  Двигающиесяв одном направлении с разными скоростями тела равных масс после удара

Абсолютно неупругий удар — удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело.

Пример:

абсолютно неупругий удар тел равных масс (покоящегося и движущегося):

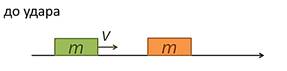
Рис. 12. Тела равных масс (покоящееся и движущееся) до удара

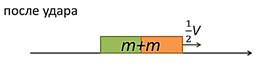
Рис. 13. Тела равных масс (покоящееся и движущееся) после удара

Общая скорость тел после неупругого удара может быть найдена из закона сохранения импульса:

m₁ʋ₁ + m₂ʋ₂ = (m₁+m₂)ʋ,

где m₁, m₂ — массы первого и второго тела, ʋ₁, ʋ₂ — скорости тел до удара, ʋ — общая скорость тел, полученная после удара.

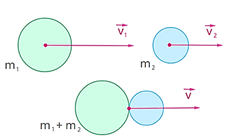
Импульсы являются величинами векторными, поэтому складываются только векторно.

Как и при любом ударе, при абсолютно неупругом ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую.

Пример:

хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.