Уравнение Менделеева – Клапейрона. Закон Дальтона. Решение задач

Уравнение Менделеева – Клапейрона. Закон Дальтона.

Решение задач

Уравнение Клапейрона при m = const: отношение произведения давления и объёма к температуре есть величина постоянная для постоянной массы газа: 

Если изменяется какой-либо макроскопический параметр газа постоянной массы, то два других параметра изменятся таким образом, чтобы указанное соотношение осталось постоянным.

Отношение произведения давления и объёма к температуре равно универсальной газовой постоянной для одного моля идеального газа: 

Уравнение Менделеева при v = 1 моль: 

Произведение постоянной Больцмана и постоянной Авогадро называется универсальной газовой постоянной.

 - уравнение состояния идеального газа.

Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона».

Закон Дальтона

Сформулирован этот закон так: общее давление смесей газов, не реагирующих друг с другом, равно сумме пар­циальных давлении составных частей (компонентов).

P = p₁ + p₂ + p₃ + ….. + p_n (14)

где Р — общее давление смеси газов; p₁, p₂, p₃, …., p_n – парциальные давления компонентов смеси.

Парциальным давлением называется давление, оказы­ваемое каждым компонентом газовой смеси, если предста­вить этот компонент занимающим объем, равный объему смеси при той же температуре. Иными словами, парциаль­ным давлением называется та часть общего давления га­зовой смеси, которая обусловлена данным газом.

Из закона Дальтона следует, что при наличии смеси газов п в уравнении (12) представляет собой сумму числа молей всех компонентов, образующих данную смесь, а Р— общее давление смеси, занимающей при температу­ре Т объем V.

Зависимость между парциальными давлениями и общим выражается уравнениями:

; ;  (15а) ,

где n₁, n₂ , n₃ — число молей компонента 1, 2, 3, соответ­ственно, в смеси газов.

Отношения называются мольными долями данного компонента.

Если мольную долю обозначить через N, то парциальное давление любого i-го компонента смеси (где i = 1,2,3,...) будет равно:  .

Таким образом, парциальное давление каждого компо­нента смеси равно произведению его мольной доли па общее давление газовой смеси.

Помимо парциального давления у газовых смесей раз­личают парциальный объем каждого из газов v₁, v₂, v₃ и т. д.

Парциальным называют объем, который занимал бы отдельный идеальный газ, входящий в состав идеальной смеси газов, если бы при том же количестве, он имел давление и температуру смеси.

Сумма парциальных объемов всех компонентов газовой смеси равна общему объему смеси

V = v₁, + v₂ + v₃ + ... + V_n (16) .

Отношение и т. д. называется объемной долей первого, второго и т.д. компонентов газовой смеси.

Для идеальных газов мольная доля равна объемной доле. Следовательно, парциальное давление каждого ком­понента смеси равно также произведению его объемной доли на общее давление смеси.

;  ;  p_i = r_i´P .

Парциальное давление обычно находят из величины общего давления с учетом состава газовой смеси. Состав газовой смеси выражают в весовых процентах, объемных процентах и в мольных процентах.

Объемным процентом называется объемная доля, уве­личенная в 100 раз (число единиц объема данного газа, содержащегося в 100 единицах объема смеси)

; 

Мольным процентом q называется мольная доля, уве­личенная в 100 раз.

; 

Весовой процент данного газа — число единиц массы его, содержащихся в 100 единицах массы газовой смеси.

; 

где m₁, m₂ – массы отдельных компонентой газовой смеси; m – общая масса смеси.

Для перехода от объемных процентов к весовым, что бывает необходимым в практических расчетах, пользуют­ся формулой: (18) ,

где r_i  (%) — объемное процентное содержание i-гo компонен­та газовой смеси; M_i —молекулярная масса этого газа; М_ср - средняя молекулярная масса смеси газов, которую вычисляют по формуле

М_ср = М₁ · r₁ + M₂ · r₂ + M₃ · r₃ + ….. + M_i´r_i (19)

где М₁, M₂, M₃, M_i — молекулярные мaccы отдельных газов.

Если состав газовой смеси выражен количеством масс отдельных компонентов, то среднюю молекулярную массу смеси можно выразить по формуле

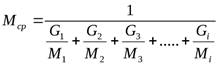(20) ,

где G₁, G₂, G₃, G_i – доли масс газов в смеси:  ;  ;  и т.д.

Решение задач

1.                 Определить давление кислорода в баллоне объемом V = 1 м³  при температуре            t=27 °С. Масса кислорода m = 0,2 кг.

2.                 Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.

3.                 При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м³. Определить молярную массу газа.

4.                 Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.

5.                 До какой температуры Т₁ надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре  Т₂ = 200 К?

6.                 В сосуде объемом 4·10^-3 м³ находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10^-6 кг /см³, если давление газа остается неизменным.

Смесь газов

7.                 В баллоне объемом 25 литров находится 20 г азота и 2 г гелия при 301К. Найдите давление в баллоне.

8.                 Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?

Задания

1.                  Установите соответствие между физическими величинами и приборами для их измерения. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Ответ:

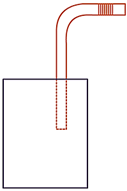2. В герметично закрытый пакет из-под сока вставлена изогнутая трубочка для коктейля (см. рисунок), внутри которой находится небольшой столбик сока. Если обхватить пакет руками и нагревать его, не оказывая на него давления, столбик сока начинает двигаться вправо к открытому концу трубочки. Выберите все утверждения, которые верно характеризуют процесс, происходящий с воздухом в пакете, и запишите номера выбранных утверждений.

1) Воздух в пакете расширяется.

2) Воздух в пакете сжимается.

3) Температура воздуха понижается.

4) Температура воздуха повышается.

5) Давление воздуха в пакете остается неизменным.

6) Давление воздуха в пакете повышается.

Решение. 1) Нагревание происходит при постоянном давлении (капелька может перемещаться), значит, объём ……

2) Происходит нагревание воздуха в пакете, температура …….

3) Так как капелька перемещается, то давление ……….