
План урока
|
Четверть: IІ Урок №5-6 9.2А: Тригонометрические функции |
|
||||
|
Дата: 31.10.18 |
ФИО учителя |
||||
|
Класс: 9F |
Количество присутствующих: |
отсутствующих: |
|||
|
Тема урока: |
Тригонометрические функции и их свойства. Формулы приведения. |
||||
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) |
9.2.4.2знать определения основных тригонометрических функций и уметь определить их свойства по единичной окружности; 9.2.4.3понимать,
как тригонометрические функции tgα и ctgα зависят
от cosα и sinα, и применять тождества 9.2.4.4знать и применять формулы приведения. |
||||
|
Цели урока: |
Учащиеся будут: знать и применять формулы приведения. |
||||
|
ЦПР |
Применение критического мышления для развития практических навыков при решении задач. |
||||
|
Критерии оценивания: |
Знает и применяет формулы приведения. |
||||
|
Языковые цели:
|
Учащиеся будут: описывать алгоритм построения графиков тригонометрических функций; описывать свойства тригонометрических функций по графическому изображению; комментировать преобразования графиков тригонометрических функций. Лексика и терминология: радиан; единичнаяокружность, тригонометрическийкруг; уголповорота; тригонометрическаяфункция; синус, косинус, тангенс, секанс, косеканс, котангенс произвольного угла; асимптоты; четность/нечетностьфункций; точкимаксимума и минимума; период; амплитуда; преобразование графиков тригонометрических функций: сжатие/растяжение, параллельный перенос вдоль осей координат, симметричное. Серия полезных фраз для диалога/письма: чтобы перевести радианы в градусы, надо…. чтобы перевести градусы в радианы, надо … направлениеповорота …… являетсяположительным. |
||||
|
Привитие ценностей: |
Сотрудничество. Академическая честность. |
||||
|
Межпредметная связь |
Навыки построения графиков тригонометрических функций и исследование их свойств необходимы учащимся для дальнейшего изучения разделов математики, в том числе раздела «Тригонометрические уравнения и неравенства», и служат основой для понимания формул физики, решению прикладных задач. |
||||
|
Навыки использования ИКТ: |
Развивать навыки работы с ActiveInspire, Презентация в PowerPoint. |
||||
|
Предварительные знания:
|
Знание понятий «функция», «аргумент». Знание графика функции и его свойств. Знание определения тригонометрических функций острого угла из курса геометрии. |
||||
|
Тип урока: |
Урок изучения нового материала и закрепления знаний. |
||||
|
Ход урока: |
|||||
|
Запланированные этапы урока |
Запланированная деятельность на уроке |
Ресурсы |
|||
|
Начало урока 10 мин
Середина урока 20 мин
10 мин
|
Оргмомент.Проверка и разбор домашнего задания. Мозговой штурм.Тригонометрический круг – тренажер. Точка-смайлик скользит по кругу, останавливаясь то на осях координат, то на различных точках круга. Учитель называет ученика и тот быстро называет значение точки (либо угол в радианах, либо значения синуса, косинуса, тангенса или котангенса на осях).
Определить знак тригонометрических функций.
Изучение новой темы. Работа в группе. Сейчас каждой группе предстоит сделать попытку добыть новые знания, используя предыдущий опыт, предыдущие знания. Каждой группе дается задание заполнить таблицу, используя формулы сложения. Командир разбивает задание на составляющие части и распределяет между членами группы. Работать можно прямо в тетрадях. Конечные результаты заносятся в общую таблицу, которая у вас на столе. На сером поле – «четверть» нужно проставить номер той четверти, куда попадает ваша исходная функция. Когда группа заполнит таблицу полностью, кто-либо из группы выносит результаты на доску. Все расчеты можно выполнять прямо в тетради. Объединив результаты работы 4-х групп, вы сами откроете и сформулируете новое правило. Таблица 1 группе:
Таблица 2 группе:
Таблица 3 группе:
Таблица 4 группе:
А также выводформул:
легко
определяется учащимися, если попросить их повернуть точку Провести рассуждения для формул
Далее попросите учащихся доказать самостоятельно на единичной окружности формулы sin (p+α) = - sinα и cos (3p/2+α) = sinα. и найти значения sin (p-α) = … и cos (3p/2-α) = ….. Результаты обсудите. sin (p+α) = - sinα.
cos (3p/2+α) = sinα. Введите «мнемоническое правило»: 1. Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить. 2.
Если под знаком преобразуемой тригонометрической функции содержится
сумма аргументов вида 3.
Перед полученной функцией от аргумента t
надо поставить тот знак, который имеет исходная функция при условии, что 4. Любая из формул приведения может быть записана и для градусной меры угла, то есть когда под знаком тригонометрической функции записано выражение вида 90° + α, 90° - α, 180° + α. Закрепление темы. Решение упражнений с комментированием учащихся с места:
|
|
|||
|
2 урок 20 мин
20 мин
|
№4. Упростить выражение:
№5. Вычислить: №6.Упростить выражение:
№7.
Доказать: Самостоятельная работа. Вариант 1. 1. Упростить выражение: а) б)
2. Вычислить: а ) б) Вариант 2. 1. Упростить выражение: а) б) а) б)
|
||||
|
Конец урока 3 мин |
Подведение итогов. Домашнее задание:по учебнику В конце урока рефлексия: Понятна ли была тема на уроке? Какие были трудности? Смогли ли вы решить задачи на уроке самостоятельно? Испытывали ли вы трудности при выполнении заданий? |
||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности |
|||
|
|
|
|
|||
|
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? |
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
||||
|
|
|||||
|
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
|||||
Приложение №1.
Таблица 1 группе:
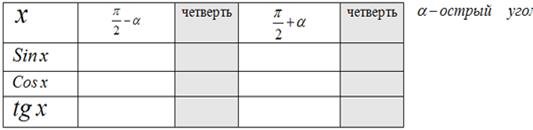
Таблица 2 группе:
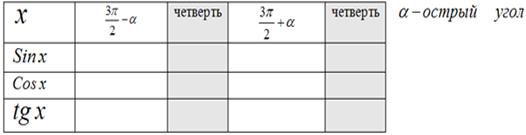
Таблица 3 группе:
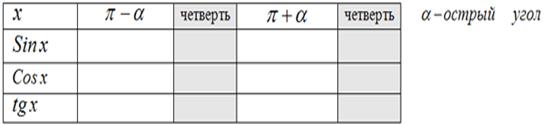
Таблица 4 группе:
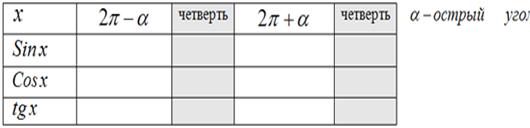


 Работа в паре.
Взаимооценивание.
Работа в паре.
Взаимооценивание.
№4. Упростить выражение:
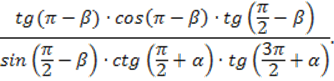
№5. Вычислить:![]()
№6.Упростить выражение: ![]()
№7.
Доказать: ![]()
Самостоятельная работа.
Вариант 1.
1. Упростить выражение:
а)
![]() ;
;
б)
![]() .
.
2. Вычислить:
а
)![]()
б)
![]()
Вариант 2.
1. Упростить выражение:
а)
![]() ;
;
б)
![]()
2. Вычислить:
а)
![]() ;
;
б)
![]() .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.