Урок алгебры по теме " Иррациональные уравнения" 8 класс

 

 

МБОУ «СОШ№26»

 

 

План- конспект открытого урока

 по математике в 11 классе

 

 

                                 

 «Решение сложных комбинированных уравнений»

 

 

Урок разработала и провела:

 Бабаева Шехла  Аликовна ,

учитель математики

МБОУ «СОШ№26»

 

 

 

 

 

 

Тип урока: семинарское занятие.

Цель урока:

закрепить навыки решения сложных уравнений различными методами.

Ход урока:

I Организационный момент:

а) готовность класса к уроку;

б) сообщение цели и задач урока.

ІI Актуализация опорных знаний со слабыми и средними учащимися, работа наиболее подготовленных учащихся по индивидуальным карточкам.

1.      Дать определение уравнения и его корня, равносильности двух уравнений.

Ответ:

Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.

2.      Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.

Ответ:

Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.

Равносильными преобразованиями уравнения являются:

·         перенос члена уравнения с противоположным знаком из одной части уравнения в другую;

·         умножение (деление) обеих частей уравнения на отличную от нуля число;

·         возведение уравнения в нечетную степень;

·         извлечение корня нечетной степени с обеих частей уравнения:

·         логарифмирование показательного уравнения;

·         применение тождеств, т. е равенств, справедливых для любого числа.

3.      Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения:

;

4.      Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.

Ответ:

Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.

Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.

При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.

Преобразованиями, приводящими к уравнению- следствия является:

·         возведение уравнения в четную степень;

·         потенцирование логарифмического уравнения;

·         освобождение уравнения от знаменателя;

·         приведение подобных членов;

·         применение формул (тригонометрических, логарифмических и других).

5.      Расскажите, каким способом приводится следующие уравнения к уравнению - следствия:

;

;

.

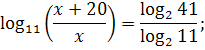
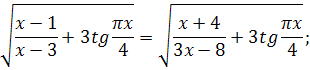
6.      Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:

1.

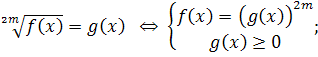
2.

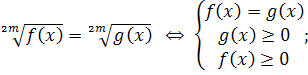
3.

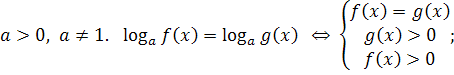
4.

5.

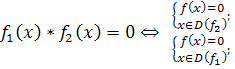
6.

7.

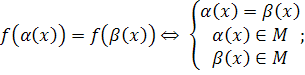
М-область существования 

8.

9.

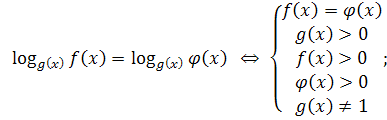
10.

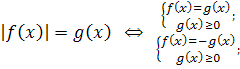
11. 

 

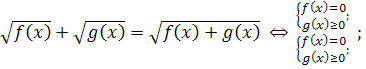
Запишите системы, равносильные уравнениям:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

7.      Решение уравнений с применением формул.

Каким способом можно решить данное уравнение:

8.      Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:

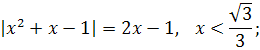
Как можно упростить решение такого типа уравнения?

Ответ:

Учитывая, что левая часть уравнения неотрицательное число получаем  значит, множество решений данного уравнения есть. Левая часть уравнения для любого  есть отрицательное число, значит, рассматривается только одно уравнение . Решается квадратное уравнение, находим и выбираем те, которые принадлежат множеству М.

9.      Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:

а)

 имеет ровно три корня.

Ответ:

Для каждого значения a рассмотрим функцию

Она определена на множестве R, четная, поэтому, если  - корень уравнения, то  - тоже является корнем уравнения.

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет  и еще два отличных от нуля корня, отличающихся знаками.

получаем: 

При  уравнение примет вид  у уравнения только один корень.

При  уравнение имеет вид . Это уравнение имеет три корня  Ответ:3

б) Найти все значения параметра а, при которых уравнение

. (2)

имеет ровно четыре корня.

Ответ:

Для каждого значения a рассмотрим функцию

Она определена на множестве R, четная.

Уравнение (2) имеет четыре корня, если уравнение имеет ровно два положительных корня, т.к. корнями уравнения (2) будут  . Значит дискриминант уравнения (3) должны быть положительными:

в) Для каждого значения параметра a решите уравнение:

Ответ:

При  уравнение не имеет решений, т.к. .

При  имеем:

Проверяем ОДЗ:

Ответ: при уравнение имеет одно решение

г) При каком значении параметра a уравнение не имеет корней:

Ответ:

корень уравнения.

Уравнение не имеет решений, если не выполняется ОДЗ, поэтому

III Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.

1.     

2.      ;

3.     

ІV Повторение. Решение заданий типа В1- В12 в интерактивном режиме с сайта www.ege.edu.ru Банк заданий типа В.

V Разбор заданий типа С с индивидуальных карточек на доске.

Карточка №1

С1.(В13) 

Карточка №2

C1.(B1)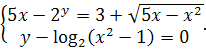 

Карточка №3

C1.(B12) 

Карточка №4

C1.(B19)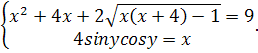 

Карточка №5

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка №6

С5. Найти все значения a, такие, что уравнение имеет единственное решение:

Карточка № 7

Найти наибольший корень уравнения:

.

Карточка № 8

Найти значение р, при которых уравнение

не имеет решений.

Карточка №9

Решить уравнение

VI Домашнее задание:

1.    Решить уравнения с параметром (б, г)

2.    Решить № 4, 6, 9 с карточек.

3.    Вариант 9 со сборника ФИПИ - разобрать В1-В12.

4.    Повторить теорию по темам:

·         §8 Уравнения-следствия.

·         §9 Равносильность уравнений системам.

·         §10 Равносильность уравнений на множествах.

VII Подведение итогов урока.

 

Скачано с www.znanio.ru