Урок. Длина окружности

План открытого урока

Учитель: Никитова-Рехлецкая Ирина Александровна

Предмет: математика

Класс: 6В

Тема: Длина окружности.

Тип урока: Урок первичного предъявления новых знаний.

Цели урока:

Вспомнить понятие окружности и ее элементов, получить практическим путем число ПИ, изучить формулы длины окружности, применить их для решения задач;

Развивать познавательный интерес учащихся, показать связь изучаемого материала с реальной жизнью;

Прививать учащимся навык совместной работы, учить аккуратности.

Оборудование: циркуль, линейка, карандаш, нить, модель круга.

План урока:

1.     Организационный этап.

Приветствие учащихся. Проверка готовности к уроку.

2.     Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Вспомните, какие геометрические фигуры мы с вами изучали, начиная с самых простых (точка, прямая, луч, отрезок, треугольник, окружность).

Запись на доске числа ПИ. Кто может вспомнить, что за обозначение я записала на доске? (число ПИ) Верно. Чему оно равно? (3, 14) Как думаете, с какой фигурой мы будем сегодня работать? С какой фигурой связано это число? (с окружностью). Ну конечно. Окружность – особая фигура. В Древней Греции окружность считалась совершеннейшей фигурой. И сейчас, когда хотят особо отметить что-либо, используют слово «круглый». Например, как называют ученика, который учится на одни пятерки? (круглый отличник).

Но с окружностью, как и с другими геометрическими фигурами, мы с вами уже знакомились в прошлом учебном году. А в этом году мы в основном занимаемся измерениями и вычислениями. Как думаете, чем мы займемся на этом уроке? Что в окружности мы можем измерить, вычислить? (будем учиться вычислять длину окружности).  Итак, цель нашего урока – вывести формулу для вычисления длины окружности и научиться ею пользоваться. Откройте тетради, запишите число 26.04 и тему урока «Длина окружности».

3.     Актуализация знаний.

Но сначала вспомним,  что же это за фигура такая – окружность, и какие основные элементы она содержит.

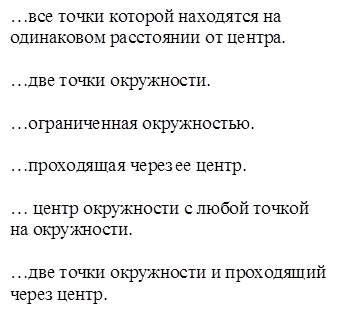
Для этого вам нужно собрать разбежавшиеся определения. В первом столбце – начало определения, а во втором -  его завершение. Задача – соединить две части определения.

А теперь найдем все названные фигуры и их элементы на рисунке. (радиус R, диаметр D, хорда, окружность, круг). Скажите, как связаны между собой окружность и круг? Чем является окружность для круга? (границей). Отлично, все знаете, что забыли – вспомнили.

4.     Первичное усвоение новых знаний.

Совсем недавно мы с вами измеряли длину отрезка. Какой инструмент нам понадобился для этого? (линейка). Как вы думаете, можно ли измерить линейкой длину окружности? Почему? А что нам может помочь в измерении? (нить, гибкий материал, который можно развернуть). Давайте попробуем измерить длину окружности. На партах вы видите модели круга. Задача – измерить длину окружности, ограничивающей данный круг. Как будем это делать? (сначала нитью опоясываем модель, затем распрямляем нить и измеряем длину получившегося отрезка нити по линейке.) Правильно, задание выполняем в парах, ребята с первого варианта выходят к доске и записывают результаты своих измерений в таблицу.

Отлично, у всех получилось измерить длину окружности. А теперь внесем в таблицу результаты еще одного измерения. Вам нужно измерить диаметр окружности. Как можно измерить диаметр?  (Приложить линейку к окружности так, чтобы прямая проходила через центр окружности, она пересечет окружность в двух точках. Отрезок, заключенный между этими точками, и нужно измерить.) Работаем также в парах. В таблицу результаты записывают ребята со второго варианта. Приступаем к работе. Отлично, наша таблица заполнена.

И теперь последняя задача. Каждый для своего варианта измерений найдите частное от деления длины окружности на ее радиус. Результат округлите до сотых и занесите в таблицу. Итак, давайте посмотрим на результаты вычислений. Что замечаем? (3, 14 и близкие к нему значения). Как думаете, какое число здесь при идеальных условиях должно было появиться? (ПИ). А почему получились близкие к нему значения, но все-таки не равные ПИ? (неточные измерения, веревка тянется, погрешности линейки). Все верно. И при устранении этих нюансов в каждой ячейке третьего столбца должно быть число ПИ. Тогда мы можем сделать вывод, что если длину окружности поделить на длину ее диаметра, то мы получим число ПИ Какой вывод можно сделать? (что при делении длины окружности на ее диаметр всегда получается 3, 14. ) А что это за значение? Мы уже вспоминали. (число ПИ). И это равенство верно для окружности любого диаметра. Запишем это утверждение в тетради: «Отношение длины окружности к длине ее диаметра равно числу ПИ»

5.     Первичная проверка понимания.

Применим полученную формулу для вычисления длины окружности. откройте учебники на стр.208 Запишите № 1031 Прочитайте задание. Что известно, что нужно найти? Какая формула потребуется для решения? У доски выполняем задания (а,б) – решение учащимися у доски, (в) – в тетрадях – проверка результата.

6.     Физкультминутка

Ну что устали считать? Теперь немного почертим окружности. Но только не с помощью циркуля. Прошу всех встать. Как думаете, можно начертить окружность головой? Пробуем. А рукой? А другой? А ногой? А другой? А двумя руками вместе. Все, и вновь сидим на месте.

7.     Первичное закрепление новых знаний.

Решим еще несколько задач.

Диаметр земного шара приближенно равен 12700 км. Чему равен радиус Земли и длина экватора Земли? (Результат округлите до сотен километров)

Длина экватора Луны приближенно равна 10900 км. Чему равен диаметр Луны? (Результат округлите до сотен километров)

Вычислите длину круговой орбиты искусственного спутника Земли, если спутник вращается на расстоянии 320км от Земли, а радиус Земли равен 6370км. (Результат округлите до сотен километров)

Дополнительно:

Ну что ж,  с задачами вы справились. А теперь давайте посмотрим, как изменится длина окружности при изменении ее радиуса. Вернемся вновь к учебникам.

№1033 (а)

Следующая задача №1035 (а)

8.     Информация о домашнем задании , инструктаж по его выполнению.

Итак, наш урок подходит к концу, откройте, пожалуйста, дневники. Запишите ДЗ на понедельник. РТ №310-314

9.     Рефлексия (подведение итогов).

Закройте дневники, подведем итоги.

С какой фигурой мы сегодня работали? (окружность)

Что нового о ней узнали? (как измерить ее длину, формулу для вычисления длины окружности)

Ну что ж, на этом урок окончен. Всем спасибо за работу.