УРОК МАТЕМАТИКИ НА ТЕМУ " Решение сложных комбинированных уравнений" 11 кл

Урок математики в 11 классе: «Решение комбинированных уравнений».

Цели урока:

-обобщение и закрепление знаний по теме «Показательные уравнения и неравенства»;

-воспитание познавательного интереса к предмету;

-формирование умений анализировать, проводить обобщение, переносить знания в новую ситуацию.

Оборудование: урок проходит в компьютерном классе.

Ход урока:

1. Организационный момент.

2. Вводное слово учителя.

Сегодня на уроке мы рассмотрим так нестандартные, так называемые, комбинированные уравнения вида f(x)=g(x) , где f(x) и g(x) – функции совершенно разного типа. Например, , 2х+2-х²=  и т.д..

Запишем число и тему урока: «Решение комбинированных уравнений».

Рассмотрим уравнение .

На первый взгляд уравнение кажется неестественным, ведь оно относится одновременно к двум большим темам «Показательная функция» и «Тригонометрические функции», которые редко пересекаются на одном уроке, а тем более - в одном уравнении. Но графический метод решения уравнений, который мы будем вспоминать на этом уроке, поможет справиться и не с такими сюрпризами. Конечно, строить графики - работа не из самых увлекательных, особенно когда приходится находить производную или вычислять значения функции в ряде точек. Но мы имеем возможность строить графики практически мгновенно с помощью программы Advanced Grapher.

3. Актуализация знаний.

Для того, чтобы успешно работать в дальнейшем, давайте вспомним основные определения и свойства функций, ответив на следующие вопросы.

- какая зависимость между величинами называется функцией?

-а теперь давайте вспомним графики некоторых известных вам функций (по данному графику функции назвать её уравнение указать область определения и область значений)

-укажите примеры функций, у которых множество значений ограничено. (показательные, тригонометрические, квадратичные, модуль, квадратный корень и т. д.)

-даны функции: у=sin x, у=3^х, у=х²+4, у=8-х² , у=|х|. Назовите их наибольшие и наименьшие значения, если таковые существуют.

4. Изучение нового материала.

Вернемся к теме нашего урока: решение комбинированных уравнений.

Существуют теоремы, способные облегчить решение таких уравнений. Сегодня мы познакомимся с одной из них.

Если на некотором промежутке I наибольшее значение функции  f(x) равно числу А, а наименьшее значение функции g(x) тоже равно числу А, то уравнение f(x)=g(x) равносильно системе

f(x)= А

g(x)=А

на данном промежутке I.

Рассмотрим применение этой теоремы при решении уравнения .

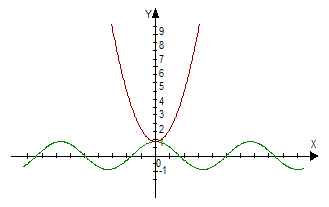
f(x) = x² + 1, g(x) = cos x,

min f(x) = 1, max g(x) = 1

x² + 1 = cos x х²+1=1х=0

                             cosx=1

Предложить ученикам пересказать теорему своими словами, переформулировать теорему применительно к графикам данных функций.

5. Закрепление изученного.

Задание 1. Выберите уравнения, для которых подходит изученная теорема:

x²+100=cosx, 48-x²=2cosx, x²+3=cosx+2, 2^x=cosx, cosx=lxl+1.

x²+3=cosx+2, cosx=lxl+1 – решить устно.

Так как при решении уравнения мы оценивали левую и правую части, то этот метод решения уравнений можно назвать методом оценки.

Задание 2. Вернёмся к уравнению, записанному в начале урока. Удовлетворяет ли оно условию теоремы?

Чтобы удостовериться в этом обратимся к компьютерам и построим графики функций, стоящих в левой и правой частях уравнения. Ведь по графику функции легче определить, ограничена она или нет.

Для того, чтобы построить на компьютере графики функций  и , вспомним, как записать формулы функций в виде, необходимом для компьютера: y=2^(x^2-4*x+5) y=sin(5*3.14*x/4)-cos(3.14*x/2).

По построенным  графикам ребята отвечают на вопросы учителя:

-какими числами ограничены графики функций по оси Оу?

-сколько общих точек имеют графики?

-удовлетворяют ли данные функции условию теоремы?

-каков корень уравнения?

Мы использовали компьютер для поиска решения данного уравнения. Давайте теперь запишем математическое решение.

Решение: рассмотрим функции  и . Функция f(x) ограничена числом 2 снизу, т.е. для всех  выполняется неравенство. Функция g(x) ограничена числом 2 сверху, т.е. для всех . Значит уравнение равносильно системе

Первое уравнение имеет единственный корень х=2. Проверкой можно убедиться, что х=2 удовлетворяет и второму уравнению. Других корней нет, так как графики данных функций пересекаются в одной точке.

Ответ: 2.

5. Самостоятельная работа на компьютере.

Задание 3. Решите уравнение х²+4х+5=cos4x.      Ответ:-2.

Задание 4. Решите уравнение .   Ответ: 1.

Задание 5. Решите уравнение 4sinх=4х²-4х+5.     Ответ: нет решения.

Творческие задания.

Задание 6. Составить уравнение по следующим рисункам:

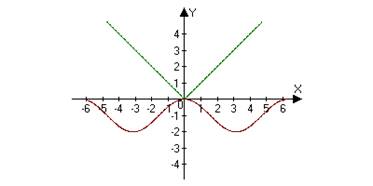
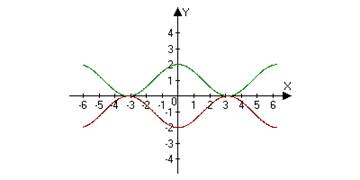
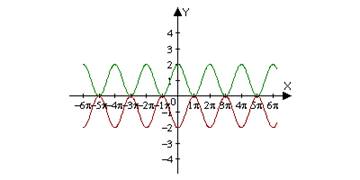
Задание 7. Придумать и выполнить рисунок, подходящий к условию теоремы.

6. Подведение итогов.

А можно ли решить данные уравнения без компьютера? Как построить график в таком случае? (с помощью производной).

Можно ли провести рассуждения без графиков? (да, опираясь на свойства функций)

Домашнее задание: решить уравнение без использования графика, опираясь на свойства функций.