
Муниципальное автономное образовательное учреждение
«Уренская средняя общеобразовательная школа №2»
Уренского муниципального района
Нижегородской области
Районный конкурс методических разработок для учителей математики «Я хочу поделиться…»
Номинация: методическая разработка учебного занятия
Урок по алгебре и началам анализа по теме: «Решение тригонометрических уравнений».
Работу выполнила: Вихарева Т.А., учитель математики
Цели урока:
Образовательные: закрепить навыки решения тригонометрических уравнений; повторить методы решения тригонометрических уравнений; познакомить учащихся с историей развития тригонометрии.
Развивающая: развитие внимания, математического мышления, речи.
Воспитательные: воспитание интереса к математике, самостоятельности, активности; формирование навыков групповой, индивидуальной деятельности в сочетании с самостоятельностью учащихся.
Требования к знаниям, умениям и способам деятельности :овладеть понятиями и умениями, связанными с решением тригонометрических уравнений; овладеть приемами оценки решений уравнений; правильно употреблять термины; уметь решать простые тригонометрические уравнения; уметь применять методы для решения тригонометрических уравнений;
Тип урока: урок обобщения и систематизации знаний.
Формы работы: индивидуальная, групповая, фронтальная.
Методы: практические.
Структура урока:
1. Организационный момент(1мин).
2. Актуализация знаний(5мин)
- устная работа «Домино»(3мин);
- повторение методов решения тригонометрических уравнений(2 мин).
3. Выполнение теста.(10мин)
4. Групповая работа учащихся(игра «Поле чудес»).(7мин)
5. Самостоятельная работа учащихся (выполнение заданий разной уровни сложности).(15мин)
6. Домашнее задание.(1мин)
7. Итоги урока.(1мин)
Ход урока
1.Организационный момент(1 мин).
Учитель: Здравствуйте ребята! Мы начинаем очередной урок алгебры. Сегодня на уроке мы повторим методы решения тригонометрических уравнений; будем выполнять тест, задания разной уровни сложности. Но сначала давайте отметим отсутствующих и проверим домашнее задание. (Учитель фиксирует отсутствующих, дежурный докладывает о выполнении домашнего задания.)
2. Актуализация знаний (5 мин).
А) Проверка домашней работы(устно).
Б) Устная работа «Домино»
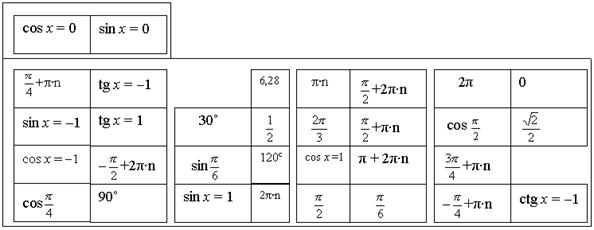
В) (Устно) Среди уравнений, данных на доске, выбрать те которые решаются
А) приведением к квадратному(№1,6,8)
Б) как однородные (№4,9)
В) с помощью введения вспомогательного аргумента (№3,10)
Г) разложением на множители (№2,7)
Д) с помощью формул суммы и разности (№5)
1. 2tg²x-tgx-3=0
2. 2cosx+3sin2x=0
3. sinx+cosx=1
4. 2sin2x+cos2x=5sinxcosx
5. sinx+sin3x=sin5x-sinx
6. 2cos2x+3sin2x+2cosx=0
7.cos2x-cosx=0
8. 8sin22x+cos2x+1=0
9. sin2x+4cos2x=1
10. 2tgx-4ctgx+7=0
3. Выполнение теста (10 мин).
Учитель: Сейчас, для поверки знаний, вам будут предложены разноуровневые тестовые задания.
|
1 вариант |
2 вариант |
|
1. Какие из данных уравнений не имеют корней? а) sinx=-0,44 б) cosx=5 в) tgx= - 10 г) ctgx=0 2.Решите уравнение и выберите правильный ответ: cos(p/2-x)= - 1 а) б) в) г) 3.Решите уравнение и выберите правильный ответ: cos(p+x)=sinp/2 а) pn , nÎZ; б) в) г) p+2pn , nÎZ. 4.Решите уравнение: tg²x-√3tgx= 0 Ответ: |
1. Какие из данных уравнений не имеют корней? а) cosx= - 0,33 б) sinx=4 в) ctgx= - 8 г) tgx=0 2. Решите уравнение и выберите правильный ответ: sin(p/2+x)=1 а) б) 2πn, nÎZ; в) г) 3.Решите уравнение и выберите правильный ответ: sin(p-x)=tgp/4 а) pn , nÎZ; б) в) г) p+2pn , nÎZ. 4.Решите уравнение: tg2x+tgx= 0 Ответ: |
После выполнения теста ученики, сидящие за одной партой, обмениваются работами и проверяют выполненные задания соседа, выставляют оценки по данным критериям. Ответы теста написаны на доске.
За правильное выполнение 2 заданий – «3», 3 – «4», 4 - «5».
4. Групповая работа (игра «Поле чудес»)(7мин)
Учитель: Перед вами карточки на которых изображены числас буквами. Ребята, вам нужно сначала решить уравнения, после найти карточки, совпадающие с ответом и расшифровать слово.
Учащиеся работают индивидуально, каждый над своим заданием.
|
Задания |
|
1.2sin2x-1=0 2. 6sin2x+sinx=2 3. sin2x-4sinxcosx+3cos2x=0 4.
2sin( 5.sin3x-sin7x=0 6. 2sin2x+sinx=1 7.cos2x-sin2x=0,5 8. 6cos2x+cosx-1=0 9. 2sinx+cosx=0 10. cos6x+cos2x=0 11.2cos( |
|
|
Ь |
|
|
О |
|
|
З |
|
|
А |
|
|
И |
|
|
М |
|
(-1)k |
Л |
|
|
- |
|
± |
Р |
|
|
Х |
|
|
Е |
Ответ: Аль-Хорезми
Учитель: Мы расшифровали сейчас фамилию известного человека – математика. Он вложил большой вклад в развитие тригонометрии
5. Самостоятельная индивидуальная работа учащихся (задания разной уровни сложности) (15 мин).
Учитель: Перед вами карточки с заданиями на оценку "3","4" и "5". Здесь даны тригонометрические уравнения. Их нужно решить. В зависимости от того какую оценку вы хотите получить, каждый из вас выберет карточку с заданиями.
Задания первого уровня
Карточки с заданиями на оценку "3".
Вариант 1 Вариант 2
Решите уравнениe методом сведения к квадратному.
2соs²x+5sinx-4=0 4-5cosx-2sin²x=0
Решите уравнениe методом разложения на множители
3cosx+2sin2x=0 5sin2x-2sinx=0
Решить однородное тригонометрическое уравнение
2sin²x-5sinxcosx+4cos²x=0 3sin²x-4sinxcosx-5cos²x=0
Задания второго уровня.
Карточки с заданиями на оценку «4» и «5».
Решить уравнения, самостоятельно выбрав метод решения.
1 вариант 2 вариант
1) cos2x – 5sinx – 3 = 0 1)cos2x + 3sinx = 2
2)sinx – cos3x = 0 2) cosx – sin3x = 0
3)2sin²x-5sinxcosx+3cos²x=0 3)4sin²x+sinxcosx-3cos²x=0
5.Домашнее задание: подготовка к контрольной работе (1мин)
Домашняя контрольная работа:
Вариант1 Вариант2
1.Решите уравнения: 1.Решите уравнения:
а) sin2x+1=0 а)cos2x-1/2=0
б) sin2x+2cos²x=0б)2sinxcosx=cosx
2. Решите неравенства: 2. Решите неравенства:
a) cosx≤-1/2 a)sinx≤√3/2
б) sinx≥-√3/2 б) Cosx≥-1/2
3.Решите уравнения: 3.Решите уравнения:
a) 7sin²x=8sinxcosx-cos²xa) 2cos²2x-1=sin4x
б)sin4x-sin7x=0 б) 2sinx+cosx=0
6.Подведение итогов урока(1 мин).
Учитель: Итак, ребята, сегодня на уроке мы с вами закрепили навыки решения тригонометрических уравнений, повторили методы их решения. А также узнали историю развития тригонометрии. Все вы молодцы, очень хорошо справились с заданиями.
Учитель аргументировано выставляет каждому ученику оценку.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.