урок по физике 9 класс

Урок 2/27. Период колебаний математического и пружинного маятников

Основной материал. Период и частота колебаний. Период колебаний математического маятника. Период колебаний пружинного маятника.

Демонстрации. Зависимость периода колебаний математического маятника от длины нити, независимость от амплитуды колебаний и массы груза. Зависимость периода колебаний  пружинного  маятника от жесткости пружины и массы груза, независимость от амплитуды колебаний. Объекты из Э. П.

Решение задач типа: Р. Т. задания 196—198, 200, 204.

На дом. § 25; задание 23 (1—4) или Р. Т. задания 195, 199, 201, 202; работа с Э. П.

РЕКОМЕНДАЦИИ ДЛЯ УЧИТЕЛЯ

В начале урока проведем проверочную работу, рассчитанную на 15 мин.

I вариант

1.  Математический маятник совершает колеба- ния между крайними положениями 1 и 3 (рис. 7). Скорость маятника максимальна, когда он находит- ся в положении...

А. 1 и 3.

Б. 1 и 2.

В. 2 и 3.

Г. 2.

Рис. 7

2. Равнодействующая сил, действующих на маят- ник (см. рис. 7), равна нулю, когда он находится в положении...

А. 1 и 3.

Б. 1 и 2.

В. 2 и 3.

Г. 2.

3. Пружинный маятник совершает колебания между крайними положениями 1 и 3 (рис. 8). Ско- рость маятника равна нулю, когда он находится в положении...

А. 1 и 3.

Б. 1 и 2.

В. 2 и 3.

Г. 2.

Рис. 8

4. Ускорение маятника (см. рис. 8) максимально, когда он находится в положении...

А. 1 и 3.   Б. 1 и 2.   В. 2 и 3.   Г. 2.

5. Какая формула выражает связь между смеще- нием и ускорением колебаний математического ма- ятника?

А. x = – g--- a.  Б. x =  g--- a.         В. x = – -l-- a.  Г. x =  -l-- a.

l              l                  g             g

II вариант

1.  Математический маятник совершает колеба- ния между крайними положениями 1 и 3 (рис. 9). Скорость маятника равна нулю, когда он находится в положении...

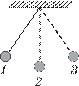А. 1 и 3.

Б. 1 и 2.

В. 2 и 3.

Г. 2.

Рис. 9

2. Равнодействующая сил, действующих на маят- ник (см. рис. 9), максимальна, когда он находится в положении...

А. 1 и 3.   Б. 1 и 2.   В. 2 и 3.   Г. 2.

3. Пружинный маятник совершает колебания между крайними положениями 1 и 3 (рис. 10). Скорость маятника максимальна, когда он находится в положении...

А. 1 и 3.

Б. 1 и 2.

В. 2 и 3.

Г. 2.

Рис. 10

4. Ускорение маятника (см. рис. 10) равно нулю, когда он находится в положении...

А. 1 и 3.   Б. 1 и 2.   В. 2 и 3.   Г. 2.

1.  Какая формула выражает связь между смеще- нием и ускорением колебаний пружинного маят- ника?

А. x = – m----- a. Б. x = m----- a.     В. x = – --k--- a.  Г. x = -k---- a.

k             k                 m            m

Ответы. I в. 1. Г. 2. Г. 3. А. 4. А. 5. А.

II в. 1. А. 2. А. 3. Г. 4. Г. 5. А.

Ход урока.

Изучение нового материала на данном уроке воз- можно осуществим по-разному. Один из вариантов заключается в том, что  совместно с учащимися устанавливаем в ходе демонстрационного экс- перимента зависимость периода колебаний от пара- метров колебательных систем. На следующем уроке учащиеся выполняют лабораторную работу № 2 и проверяют в ходе эксперимента полученные зависи- мости. Этот вариант отражен в планировании.

Второй вариант, являющийся предпочтительным, предполагаем, что учащиеся выполняют лабо- раторную работу № 2 и получают зависимость пе- риода колебаний от параметров колебательных си- стем в процессе  экспериментальной  деятельности. В этом случае появляется возможность выполнить лабораторную работу № 3* «Измерение ускорения свободного падения с помощью математического маятника».